Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-08T14:30:52.433Z Has data issue: false hasContentIssue false
  • English
  • Français

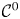$\mathbb {\mathcal {C}}^{0}$-rigidity of Lagrangian submanifolds and punctured holomorphic disks in the cotangent bundle

Part of: Symplectic geometry, contact geometry

Published online by Cambridge University Press:  03 November 2021

Cedric Membrez  and
Emmanuel Opshtein
Cedric Membrez
Affiliation:
UBS Emerging Technology Research, Zurich, [email protected]
Emmanuel Opshtein
Affiliation:
UFR de mathématiques, Université de Strasbourg, 7 rue René Descartes, 67084Strasbourg, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Our main result is the $\mathbb {\mathcal {C}}^{0}$-rigidity of the area spectrum and the Maslov class of Lagrangian submanifolds. This relies on the existence of punctured pseudoholomorphic disks in cotangent bundles with boundary on the zero section, whose boundaries represent any integral homology class. We discuss further applications of these punctured disks in symplectic geometry.

Keywords

$\mathbb {\mathcal {C}}^{0}$-symplectic geometryLagrangian rigidity

MSC classification

Primary: 53D05: Symplectic manifolds, general 53D12: Lagrangian submanifolds; Maslov index
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 11 , November 2021 , pp. 2433 - 2493
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Cedric Membrez has been partially supported by Swiss National Science Foundation grant 155540 and European Research Council Advanced grant 338809.

References

Abbas, C., An Introduction to Compactness Results in Symplectic Field Theory (Springer, Berlin, 2014).10.1007/978-3-642-31543-5CrossRefGoogle Scholar
Abbondandolo, A. and Schwarz, M., On the Floer homology of cotangent bundles, Comm. Pure Appl. Math. 59 (2006), 254–316.10.1002/cpa.20090CrossRefGoogle Scholar
Abouzaid, M., A cotangent fibre generates the Fukaya category, Adv. Math. 228 (2011), 894–939.CrossRefGoogle Scholar
Abraham, R., Bumpy metrics, in Global Analysis (Proceedings of Symposia in Pure Mathematics, Vol. XIV, Berkeley, Calif., 1968) (American Mathematical Society, Providence, RI, 1970), 1–3.Google Scholar
Amorim, L., Oh, Y.-G. and Oliveira dos Santos, J., Exact Lagrangian submanifolds, Lagrangian spectral invariants and Aubry-Mather theory, Math. Proc. Cambridge Philos. Soc. 165 (2018), 411–434.10.1017/S0305004117000561CrossRefGoogle Scholar
Anosov, D. V., Generic properties of closed geodesics, Izv. Akad. Nauk SSSR Ser. Mat. 46 (1982), 675–709, 896.Google Scholar
Besson, G., Courtois, G. and Gallot, S., Entropies et rigidités des espaces localement symétriques de courbure strictement négative, Geom. Funct. Anal. 5 (1995), 731–799.10.1007/BF01897050CrossRefGoogle Scholar
Bourgeois, F., Eliashberg, Y., Hofer, H., Wysocki, K. and Zehnder, E., Compactness results in symplectic field theory, Geom. Topol. 7 (2003), 799–888.10.2140/gt.2003.7.799CrossRefGoogle Scholar
Buhovsky, L., Entov, M. and Polterovich, L., Poisson brackets and symplectic invariants, Selecta Math. (N.S.) 18 (2012), 89–157.CrossRefGoogle Scholar
Buhovsky, L., Humilière, V. and Seyfaddini, S., A $C^{0}$ counterexample to the Arnold conjecture, Invent. Math. 213 (2018), 759–809.10.1007/s00222-018-0797-xCrossRefGoogle Scholar
Buhovsky, L. and Opshtein, E., Some quantitative results in $\mathbb {\mathcal {C}}^{0}$ symplectic geometry, Invent. Math. 205 (2016), 1–56.10.1007/s00222-015-0626-4CrossRefGoogle Scholar
Chavel, I., Riemannian Geometry: A Modern Introduction, Cambridge Studies in Advanced Mathematics (Cambridge University Press, Cambridge, 2006).10.1017/CBO9780511616822CrossRefGoogle Scholar
Chekanov, Y. V., Lagrangian intersections, symplectic energy, and areas of holomorphic curves, Duke Math. J. 95 (1998), 213–226.CrossRefGoogle Scholar
Cieliebak, K. and Mohnke, K., Punctured holomorphic curves and Lagrangian embeddings, Invent. Math. 212 (2018), 213–295.10.1007/s00222-017-0767-8CrossRefGoogle Scholar
Courte, S., Contact manifolds with symplectomorphic symplectizations, Geom. Topol. 18 (2014), 1–15.10.2140/gt.2014.18.1CrossRefGoogle Scholar
Croke, C. B. and Kleiner, B., Conjugacy and rigidity for manifolds with a parallel vector field, J. Differential Geom. 39 (1994), 659–680.CrossRefGoogle Scholar
Dimitroglou Rizell, G., Goodman, E. and Ivrii, A., Lagrangian isotopy of tori in $S^{2}\times S^{2}$ and $\Bbb {C}P^{2}$, Geom. Funct. Anal. 26 (2016), 1297–1358.10.1007/s00039-016-0388-1CrossRefGoogle Scholar
Dragnev, D. L., Fredholm theory and transversality for noncompact pseudoholomorphic maps in symplectizations, Comm. Pure Appl. Math. 57 (2004), 726–763.10.1002/cpa.20018CrossRefGoogle Scholar
Elĭasson, H. I., Geometry of manifolds of maps, J. Differential Geom. 1 (1967), 169–194.10.4310/jdg/1214427887CrossRefGoogle Scholar
Entov, M., Ganor, Y. and Membrez, C., Lagrangian isotopies and symplectic function theory, Comment. Math. Helv. 93 (2018), 829–882.10.4171/CMH/451CrossRefGoogle Scholar
Grigor'yants, A. A., On an interpretation of the torsion tensor of a connection, Izv. Vyssh. Uchebn. Zaved. Mat. 42 (1998), 22–28.Google Scholar
Gromov, M., Metric Structures for Riemannian and Non-Riemannian Spaces, Progress in Mathematics, vol. 152 (Birkhäuser, Boston, 1999). Based on the 1981 French original [MR0682063 (85e:53051)], with appendices by M. Katz, P. Pansu and S. Semmes, translated from the French by Sean Michael Bates.Google Scholar
Gutt, J., The Conley-Zehnder index for a path of symplectic matrices, Preprint (2012), arXiv:1201.3728.Google Scholar
Hofer, H., Wysocki, K. and Zehnder, E., Properties of pseudoholomorphic curves in symplectisations. I. Asymptotics, Ann. Inst. H. Poincaré Anal. Non Linéaire 13 (1996), 337–379.10.1016/S0294-1449(16)30108-1CrossRefGoogle Scholar
Hofer, H., Wysocki, K. and Zehnder, E., Properties of pseudoholomorphic curves in symplectizations. III. Fredholm theory, in Topics in Nonlinear Analysis, Progress in Nonlinear Differential Equations and Their Applications, vol. 35 (Birkhäuser, Basel, 1999), 381–475.10.1007/978-3-0348-8765-6_18CrossRefGoogle Scholar
Humilière, V., Leclercq, R. and Seyfaddini, S., Coisotropic rigidity and $C^{0}$-symplectic geometry, Duke Math. J. 164 (2015), 767–799.CrossRefGoogle Scholar
Humilière, V., Leclercq, R. and Seyfaddini, S., Reduction of symplectic homeomorphisms, Ann. Sci. Éc. Norm. Supér. (4) 49 (2016), 633–668.CrossRefGoogle Scholar
Ivashkovich, S. and Sukhov, A., Schwarz reflection principle, boundary regularity and compactness for $J$-complex curves, Ann. Inst. Fourier (Grenoble) 60 (2010), 1489–1513.10.5802/aif.2562CrossRefGoogle Scholar
Kragh, T., Parametrized ring-spectra and the nearby Lagrangian conjecture, Geom. Topol. 17 (2013), 639–731; with an appendix by Mohammed Abouzaid.CrossRefGoogle Scholar
Laudenbach, F. and Sikorav, J.-C., Hamiltonian disjunction and limits of Lagrangian submanifolds, Int. Math. Res. Not. IMRN 1994 (1994), 161–168.CrossRefGoogle Scholar
McDuff, D. and Salamon, D., Introduction to Symplectic Topology, Oxford Mathematical Monographs (Clarendon Press, Oxford, 1995).Google Scholar
McDuff, D. and Salamon, D., J-Holomorphic Curves and Symplectic Topology, American Mathematical Society Colloquium Publications, vol. 52, second edition (American Mathematical Society, Providence, RI, 2012).Google Scholar
Micallef, M. J. and White, B., The structure of branch points in minimal surfaces and in pseudoholomorphic curves, Ann. of Math. (2) 141 (1995), 35–85.10.2307/2118627CrossRefGoogle Scholar
Opshtein, E., $\mathbb {\mathcal {C}}^{0}$-rigidity of characteristics in symplectic geometry, Ann. Sci. Éc. Norm. Supér. (4) 42 (2009), 857–864.10.24033/asens.2111CrossRefGoogle Scholar
Paternain, G. P., Polterovich, L. and Siburg, K. F., Boundary rigidity for Lagrangian submanifolds, non-removable intersections, and Aubry-Mather theory, Mosc. Math. J. 3 (2003), 593–619.10.17323/1609-4514-2003-3-2-593-619CrossRefGoogle Scholar
Salamon, D., Lectures on Floer homology, in Symplectic Geometry and Topology (Park City, UT, 1997), IAS/Park City Mathematics Series, vol. 7 (American Mathematical Society, Providence, RI, 1999), 143–229.10.1090/pcms/007/05CrossRefGoogle Scholar
Salamon, D. A. and Weber, J., Floer homology and the heat flow, Geom. Funct. Anal. 16 (2006), 1050–1138.10.1007/s00039-006-0577-4CrossRefGoogle Scholar
Schwarz, M., Cohomology operations from $S^{1}$-cobordisms in Floer homology. PhD thesis, ETH Zurich (1995).Google Scholar
Sikorav, J.-C., Rigidité symplectique dans le cotangent de $T^{n}$, Duke Math. J. 59 (1989), 759–763.10.1215/S0012-7094-89-05935-8CrossRefGoogle Scholar
Smale, S., An infinite dimensional version of Sard's theorem, Amer. J. Math. 87 (1965), 861–866.CrossRefGoogle Scholar
Wendl, C., Automatic transversality and orbifolds of punctured holomorphic curves in dimension four, Comment. Math. Helv. 85 (2010), 347–407.10.4171/CMH/199CrossRefGoogle Scholar
Wendl, C., Lectures on symplectic field theory, Preprint (2016), arXiv:1612.01009.Google Scholar
Zehmisch, K., The codisc radius capacity, Electron. Res. Announc. Math. Sci. 20 (2013), 77–96.Google Scholar