Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-26T14:34:12.743Z Has data issue: false hasContentIssue false
  • English
  • Français

A Markov model for Selmer ranks in families of twists

Part of: Markov processes Arithmetic algebraic geometry

Published online by Cambridge University Press:  30 June 2014

Zev Klagsbrun ,
Barry Mazur  and
Karl Rubin
Zev Klagsbrun
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, Madison, WI 53706, USA email [email protected] Current address: Center for Communications Research, 4320 Westerra Court, San Diego, CA 92121, USA
Barry Mazur
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA email [email protected]
Karl Rubin
Affiliation:
Department of Mathematics, UC Irvine, Irvine, CA 92697, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the distribution of 2-Selmer ranks in the family of quadratic twists of an elliptic curve 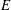$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}E$ over an arbitrary number field 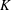$K$. Under the assumption that 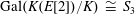${\rm Gal}(K(E[2])/K) \ {\cong }\ S_3$, we show that the density (counted in a nonstandard way) of twists with Selmer rank $r$ exists for all positive integers $r$, and is given via an equilibrium distribution, depending only on a single parameter (the ‘disparity’), of a certain Markov process that is itself independent of 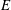$E$ and 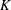$K$. More generally, our results also apply to 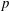$p$-Selmer ranks of twists of two-dimensional self-dual 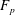${\bf F}_p$-representations of the absolute Galois group of 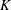$K$ by characters of order 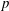$p$.

Keywords

elliptic curvesquadratic twistsSelmer groupsMarkov processesarithmetic statistics

MSC classification

Secondary: 11G05: Elliptic curves over global fields 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 7 , July 2014 , pp. 1077 - 1106
Copyright
© The Author(s) 2014 

References

Bhargava, M. and Shankar, A., Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves, Ann. of Math. (2), to appear,arXiv:1006.1002.Google Scholar
Bhargava, M. and Shankar, A., Ternary cubic forms having bounded invariants, and the existence of a positive proportion of elliptic curves having rank 0, Ann. of Math. (2), to appear, arXiv:1007.0052.Google Scholar
Bhargava, M., Kane, D., Lenstra, H. W., Poonen, B. and Rains, E., Modeling the distribution of ranks, Selmer groups, and Shafarevich-Tate groups of elliptic curves, to appear,arXiv:1304.3971.Google Scholar
Friedlander, J. B., Iwaniec, H., Mazur, B. and Rubin, K., The spin of prime ideals, Invent. Math. 193 (2013), 697–749.CrossRefGoogle Scholar
Heath-Brown, D. R., The size of Selmer groups for the congruent number problem II, Invent. Math. 118 (1994), 331–370.Google Scholar
Kane, D., On the ranks of the 2-Selmer groups of twists of a given elliptic curve, Algebra Number Theory 7 (2013), 1253–1279.Google Scholar
Klagsbrun, Z., Selmer ranks of quadratic twists of elliptic curves with partial rational two-torsion, to appear, arXiv:1201.5408.Google Scholar
Klagsbrun, Z., Mazur, B. and Rubin, K., Disparity in Selmer ranks of quadratic twists of elliptic curves, Ann. of Math. (2) 178 (2013), 287–320.CrossRefGoogle Scholar
Kramer, K., Arithmetic of elliptic curves upon quadratic extension, Trans. Amer. Math. Soc. 264 (1981), 121–135.CrossRefGoogle Scholar
Mazur, B. and Rubin, K., Selmer companion curves, Trans. Amer. Math Soc., to appear.Google Scholar
Mazur, B., Rubin, K. and Silverberg, A., Twisting commutative algebraic groups, J. Algebra 314 (2007), 419–438.Google Scholar
Milne, J. S., Arithmetic duality theorems, Perspectives in Mathematics, vol. 1 (Academic Press, Orlando, FL, 1986).Google Scholar
Norris, J. R., Markov chains (Cambridge University Press, Cambridge, 1997).CrossRefGoogle Scholar
Poonen, B. and Rains, E., Random maximal isotropic subspaces and Selmer groups, J. Amer. Math. Soc. 25 (2012), 245–269.Google Scholar
Serre, J.-P., Cohomologie galoisienne, Lecture Notes in Mathematics, vol. 5 (Springer, Berlin, New York, 1965).CrossRefGoogle Scholar
Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15 (1972), 259–331.Google Scholar
Serre, J.-P., Quelques applications du théorème de Chebotarev, Publ. Math. Inst. Hautes Études Sci. 54 (1981), 123–201.CrossRefGoogle Scholar
Stark, H., Some effective cases of the Brauer-Siegel theorem, Invent. Math. 23 (1974), 135–152.Google Scholar
Swinnerton-Dyer, H. P. F., The effect of twisting on the 2-Selmer group, Math. Proc. Cambridge Philos. Soc. 145 (2008), 513–526.CrossRefGoogle Scholar
Tate, J., Duality theorems in Galois cohomology over number fields, in Proceedings of International Congress in Mathematics (Stockholm, 1962), 234–241.Google Scholar