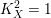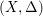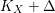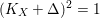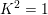Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Franciosi, Marco
Pardini, Rita
and
Rollenske, Sönke
2015.
Computing invariants of semi-log-canonical surfaces.
Mathematische Zeitschrift,
Vol. 280,
Issue. 3-4,
p.
1107.
Franciosi, Marco
Pardini, Rita
and
Rollenske, Sönke
2017.
Gorenstein stable surfaces with KX2=1 and pg>0.
Mathematische Nachrichten,
Vol. 290,
Issue. 5-6,
p.
794.
Chen, Jingshan
2018.
Normal Gorenstein stable log surfaces with (KX + Λ)2 = pg(X, Λ)−1.
Communications in Algebra,
Vol. 46,
Issue. 9,
p.
4120.
Coughlan, Stephen
and
Urzúa, Giancarlo
2018.
On $\boldsymbol{{\mathbb Z}/3}$-Godeaux Surfaces.
International Mathematics Research Notices,
Vol. 2018,
Issue. 18,
p.
5609.
Franciosi, Marco
Pardini, Rita
and
Rollenske, Sönke
2018.
Gorenstein stable Godeaux surfaces.
Selecta Mathematica,
Vol. 24,
Issue. 4,
p.
3349.
Han, Xiayimei
Robles, Colleen
and
Clingher, Adrian
2020.
Hodge Representations.
Experimental Results,
Vol. 1,
Issue. ,
Chen, Jingshan
2020.
Gorenstein stable log surfaces with (KX+Λ)2=pg(X,Λ)−1.
Communications in Algebra,
Vol. 48,
Issue. 7,
p.
2781.
Green, Mark
and
Griffiths, Phillip
2021.
Positivity of vector bundles and Hodge theory.
International Journal of Mathematics,
Vol. 32,
Issue. 12,
Do, Anh Thi
and
Rollenske, Sönke
2022.
Gorenstein stable surfaces with KX2=1 and χ(OX)=2.
Communications in Algebra,
Vol. 50,
Issue. 10,
p.
4218.
Brown, Morgan V
2022.
The Dual Complex of a Semi-log Canonical Surface.
International Mathematics Research Notices,
Vol. 2022,
Issue. 10,
p.
7495.
Rollenske, Sönke
2023.
Extra Connected Components in the Moduli Space of Stable Surfaces.
International Mathematics Research Notices,
Vol. 2023,
Issue. 11,
p.
9653.