Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-21T18:36:56.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Logarithmic growth filtrations for 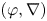$(\varphi ,\nabla )$-modules over the bounded Robba ring

Part of: Arithmetic problems. Diophantine geometry Differential and difference algebra

Published online by Cambridge University Press:  04 June 2021

Shun Ohkubo
Shun Ohkubo*
Affiliation:
Graduate School of Mathematics, Nagoya University, Furocho, Chikusaku, Nagoya464-8602, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the 1970s, Dwork defined the logarithmic growth (log-growth for short) filtrations for 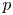$p$-adic differential equations 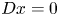$Dx=0$ on the 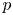$p$-adic open unit disc 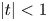$|t|<1$, which measure the asymptotic behavior of solutions 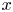$x$ as 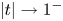$|t|\to 1^{-}$. Then, Dwork calculated the log-growth filtration for 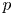$p$-adic Gaussian hypergeometric differential equation. In the late 2000s, Chiarellotto and Tsuzuki proposed a fundamental conjecture on the log-growth filtrations for 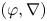$(\varphi ,\nabla )$-modules over 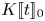$K[\![t]\!]_0$, which can be regarded as a generalization of Dwork's calculation. In this paper, we prove a generalization of the conjecture to 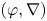$(\varphi ,\nabla )$-modules over the bounded Robba ring. As an application, we prove a generalization of Dwork's conjecture proposed by Chiarellotto and Tsuzuki on the specialization property for log-growth Newton polygons.

Keywords

p-adic differential equationslogarithmic growthPicard–Fuchs equations

MSC classification

Primary: 12H25: $p$-adic differential equations
Secondary: 14G22: Rigid analytic geometry
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 6 , June 2021 , pp. 1265 - 1301
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, Y., Dwork's conjecture on the logarithmic growth of solutions of $p$-adic differential equations, Compos. Math. 144 (2008), 484–494.CrossRefGoogle Scholar
Chiarellotto, B. and Tsuzuki, N., Logarithmic growth and Frobenius filtrations for solutions of $p$-adic differential equations, J. Inst. Math. Jussieu 8 (2009), 465–505.CrossRefGoogle Scholar
Chiarellotto, B. and Tsuzuki, N., Log-growth filtration and Frobenius slope filtration of $F$-isocrystals at the generic and special points, Doc. Math. 16 (2011), 33–69.Google Scholar
Crew, R., Finiteness theorems for the cohomology of an overconvergent isocrystal on a curve, Ann. Sci. Éc. Norm. Supér. (4) 31 (1998), 717–763.CrossRefGoogle Scholar
Dwork, B., On $p$-adic differential equations. III. On $p$-adically bounded solutions of ordinary linear differential equations with rational function coefficients, Invent. Math. 20 (1973), 35–45.CrossRefGoogle Scholar
Dwork, B., Lectures on p-adic differential equations, Grundlehren der Mathematischen Wissenschaften, vol. 253 (Springer, New York, 1982), with an Appendix by Alan Adolphson.CrossRefGoogle Scholar
de Jong, A.J., Homomorphisms of Barsotti-Tate groups and crystals in positive characteristic, Invent. Math. 134 (1998), 301–333.CrossRefGoogle Scholar
Kedlaya, K., A $p$-adic local monodromy theorem, Ann. of Math. (2) 160 (2004), 93–184.CrossRefGoogle Scholar
Kedlaya, K., Local monodromy of $p$-adic differential equations: an overview, Int. J. Number Theory 1 (2005), 109–154.CrossRefGoogle Scholar
Kedlaya, K., Slope filtrations revisited, Doc. Math. 10 (2005), 447–525.Google Scholar
Kedlaya, K., Slope filtrations for relative Frobenius, Astérisque 319 (2008), 259–301.Google Scholar
Kedlaya, K., p-adic differential equations, Cambridge Studies in Advanced Mathematics, vol. 125 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Liu, R., Slope filtrations in families, J. Inst. Math. Jussieu 12 (2013), 249–296.CrossRefGoogle Scholar
Ohkubo, S., A note on logarithmic growth Newton polygons of $p$-adic differential equations, Int. Math. Res. Not. IMRN 2015 (2015), 2671–2677.Google Scholar
Ohkubo, S., On the rationality and continuity of logarithmic growth filtration of solutions of $p$-adic differential equations, Adv. Math. 308 (2017), 83–120.CrossRefGoogle Scholar
Robert, A., A course in p-adic analysis, Graduate Texts in Mathematics, vol. 198 (Springer, New York, 2000).CrossRefGoogle Scholar
Tsuzuki, N., Slope filtration of quasi-unipotent overconvergent $F$-isocrystals, Ann. Inst. Fourier (Grenoble) 48 (1998), 379–412.CrossRefGoogle Scholar