Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T12:25:04.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Localization and nilpotent spaces in 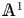${\mathbb {A}}^1$-homotopy theory

Part of: (Co)homology theory Higher algebraic $K$-theory Linear algebraic groups and related topics Homotopy theory

Published online by Cambridge University Press:  27 May 2022

Aravind Asok ,
Jean Fasel  and
Michael J. Hopkins
Aravind Asok
Affiliation:
Department of Mathematics, University of Southern California, 3620 S. Vermont Ave., Los Angeles, CA 90089-2532, USA [email protected]
Jean Fasel
Affiliation:
Institut Fourier - UMR 5582, Université Grenoble Alpes, 100, rue des Mathématiques, F-38402 Saint Martin d'Hères, France [email protected]
Michael J. Hopkins
Affiliation:
Department of Mathematics, Harvard University, One Oxford Street, Cambridge, MA 02138, USA [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a subring 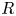$R$ of the rational numbers, we study 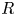$R$-localization functors in the local homotopy theory of simplicial presheaves on a small site and then in 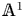${\mathbb {A}}^1$-homotopy theory. To this end, we introduce and analyze two notions of nilpotence for spaces in 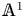${\mathbb {A}}^1$-homotopy theory, paying attention to future applications for vector bundles. We show that 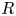$R$-localization behaves in a controlled fashion for the nilpotent spaces we consider. We show that the classifying space 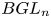$BGL_n$ is 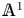${\mathbb {A}}^1$-nilpotent when 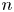$n$ is odd, and analyze the (more complicated) situation where 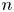$n$ is even as well. We establish analogs of various classical results about rationalization in the context of 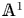${\mathbb {A}}^1$-homotopy theory: if 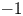$-1$ is a sum of squares in the base field, 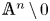${\mathbb {A}}^n \,{\setminus}\, 0$ is rationally equivalent to a suitable motivic Eilenberg–Mac Lane space, and the special linear group decomposes as a product of motivic spheres.

Keywords

motivic homotopynilpotent spaces

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 19D45: Higher symbols, Milnor $K$-theory 20G15: Linear algebraic groups over arbitrary fields 55P60: Localization and completion
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 3 , March 2022 , pp. 654 - 720
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

AA was partially supported by National Science Foundation Awards DMS-1254892 and DMS-1802060. MJH was partially supported by National Science Foundation Awards DMS-0906194, DMS-1510417 and DMS-1810917.

References

Abe, E., Chevalley groups over local rings, Tohoku Math. J. (2) 21 (1969), 474–494.CrossRefGoogle Scholar
Asok, A., Doran, B. and Fasel, J., Smooth models of motivic spheres and the clutching construction, Int. Math. Res. Not. IMRN 2017 (2017), 1890–1925.Google Scholar
Asok, A. and Fasel, J., Algebraic vector bundles on spheres, J. Topol. 7 (2014), 894–926.CrossRefGoogle Scholar
Asok, A. and Fasel, J., A cohomological classification of vector bundles on smooth affine threefolds, Duke Math. J. 163 (2014), 2561–2601.10.1215/00127094-2819299CrossRefGoogle Scholar
Asok, A. and Fasel, J., Comparing Euler classes, Q. J. Math. 67 (2016), 603–635.Google Scholar
Asok, A. and Fasel, J., An explicit $KO$-degree map and applications, J. Topol. 10 (2017), 268–300.10.1112/topo.12007CrossRefGoogle Scholar
Asok, A., Fasel, J. and Hopkins, M. J., Algebraic vector bundles and $p$-local ${\mathbb {A}}^1$-homotopy theory, Preprint (2020), arXiv:2008.03363.Google Scholar
Asok, A., Hoyois, M. and Wendt, M., Affine representability results in ${\mathbb {A}}^1$-homotopy theory I: Vector bundles, Duke Math. J. 166 (2017), 1923–1953.10.1215/00127094-0000014XCrossRefGoogle Scholar
Asok, A., Hoyois, M. and Wendt, M., Affine representability results in $\Bbb A^1$-homotopy theory, II: Principal bundles and homogeneous spaces, Geom. Topol. 22 (2018), 1181–1225.CrossRefGoogle Scholar
Asok, A., Hoyois, M. and Wendt, M., Affine representability results in $\mathbb {A}^1$-homotopy theory III: Finite fields and complements, Algebr. Geom. 7 (2020), 634–644.10.14231/AG-2020-023CrossRefGoogle Scholar
Asok, A., Wickelgren, K. and Williams, T. B., The simplicial suspension sequence in $\mathbb {A}^1$-homotopy, Geom. Topol. 21 (2017), 2093–2160.CrossRefGoogle Scholar
Bass, H., Clifford algebras and spinor norms over a commutative ring, Amer. J. Math. 96 (1974), 156–206.10.2307/2373586CrossRefGoogle Scholar
Biglari, S., Motives of reductive groups, Amer. J. Math. 134 (2012), 235–257.CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and higher $K$-theory, Adv. in Math. 61 (1986), 267–304.10.1016/0001-8708(86)90081-2CrossRefGoogle Scholar
Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations, Lecture Notes in Mathematics, vol. 304 (Springer, Berlin, 1972).10.1007/978-3-540-38117-4CrossRefGoogle Scholar
Casacuberta, C. and Peschke, G., Localizing with respect to self-maps of the circle, Trans. Amer. Math. Soc. 339 (1993), 117–140.CrossRefGoogle Scholar
Cazanave, C., Algebraic homotopy classes of rational functions, Ann. Sci. Éc. Norm. Supér. (4) 45 (2012), 511–534.CrossRefGoogle Scholar
Choudhury, U. and Hogadi, A., The Hurewicz map in motivic homotopy theory, Preprint (2021), arXiv:2101.01489.Google Scholar
Cisinski, D.-C. and Déglise, F., Triangulated categories of mixed motives, Springer Monographs in Mathematics (Springer, Cham, 2019).CrossRefGoogle Scholar
Conrad, B., Reductive group schemes, in Autour des schémas en groupes. Vol. I, Panor. Synthèses, vol. 42/43 (Société Mathématique de France, Paris, 2014), 93–444.Google Scholar
Déglise, F., Finite correspondences and transfers over a regular base, in Algebraic cycles and motives. Vol. 1, London Mathematical Society Lecture Note Series, vol. 343 (Cambridge University Press, Cambridge, 2007), 138–205.10.1017/CBO9780511721496.005CrossRefGoogle Scholar
Déglise, F., Motifs génériques, Rend. Semin. Mat. Univ. Padova 119 (2008), 173–244.CrossRefGoogle Scholar
Deligne, P., Voevodsky's lectures on motivic cohomology 2000/2001, in Algebraic topology, Abel Symposium, vol. 4 (Springer, Berlin, 2009), 355–409.CrossRefGoogle Scholar
Dwyer, W. G. and Kan, D. M., Function complexes in homotopical algebra, Topology 19 (1980), 427–440.CrossRefGoogle Scholar
Elman, R., Karpenko, N. and Merkurjev, A., The algebraic and geometric theory of quadratic forms, American Mathematical Society Colloquium Publications, vol. 56 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Fasel, J., Groupes de Chow-Witt, Mém. Soc. Math. Fr. (N.S.) 113 (2008).Google Scholar
Fasel, J., A degree map on unimodular rows, J. Ramanujan Math. Soc. 27 (2012), 23–42.Google Scholar
Goerss, P. G., Simplicial chains over a field and $p$-local homotopy theory, Math. Z. 220 (1995), 523–544.10.1007/BF02572629CrossRefGoogle Scholar
Gross, B. H., On the motive of a reductive group, Invent. Math. 130 (1997), 287–313.CrossRefGoogle Scholar
Guzman, G., Rational and $p$-local motivic homotopy theory, Preprint (2019), arXiv:1911.05061.Google Scholar
Harris, B., On the homotopy groups of the classical groups, Ann. of Math. (2) 74 (1961), 407–413.CrossRefGoogle Scholar
Hilton, P., Mislin, G. and Roitberg, J., Localization of nilpotent groups and spaces, North-Holland Mathematics Studies, vol. 15 (North-Holland, Amsterdam, 1975).10.1016/S0304-0208(08)72790-7CrossRefGoogle Scholar
Hirschhorn, P. S., Model categories and their localizations, Mathematical Surveys and Monographs, vol. 99 (American Mathematical Society, Providence, RI, 2003).Google Scholar
Hollander, S., A homotopy theory for stacks, Israel J. Math. 163 (2008), 93–124.CrossRefGoogle Scholar
Hopf, H., Über die Bettischen Gruppen, die zu einer beliebigen Gruppe gehören, Comment. Math. Helv. 17 (1945), 39–79.10.1007/BF02566234CrossRefGoogle Scholar
Hovey, M., Model categories, Mathematical Surveys and Monographs, vol. 63 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Hoyois, M., From algebraic cobordism to motivic cohomology, J. Reine Angew. Math. 702 (2015), 173–226.Google Scholar
Jardine, J. F., Motivic symmetric spectra, Doc. Math. 5 (2000), 445–552.Google Scholar
Jardine, J. F., Stacks and the homotopy theory of simplicial sheaves, Homology Homotopy Appl. 3 (2001), 361–384.CrossRefGoogle Scholar
Jardine, J. F., Local homotopy theory, Springer Monographs in Mathematics (Springer, New York, 2015).CrossRefGoogle Scholar
Kahn, B., Algebraic K-theory, algebraic cycles and arithmetic geometry, in Handbook of K-theory. Vol. 1 (Springer, Berlin, 2005), 351–428.CrossRefGoogle Scholar
Levine, M., Bloch's higher Chow groups revisited, Astérisque 226 (1994), 235–320.Google Scholar
Levine, M., Slices and transfers, Doc. Math. Extra vol. (2010), 393–443 (Andrei A. Suslin sixtieth birthday).Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
Mac Lane, S., Categories for the working mathematician, second edition, Graduate Texts in Mathematics, vol. 5 (Springer, New York, 1998).Google Scholar
Matsumoto, H., Subgroups of finite index in certain arithmetic groups, in Algebraic Groups and Discontinuous Subgroups (Proc. Sympos. Pure Math., Boulder, Colo., 1965) (American Mathematical Society, Providence, RI, 1966), 99–103.CrossRefGoogle Scholar
May, J. P. and Ponto, K., Localization, completion, and model categories, in More concise algebraic topology, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, 2012).Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture notes on motivic cohomology, Clay Mathematics Monographs, vol. 2 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Morel, F., On the motivic $\pi _0$ of the sphere spectrum, in Axiomatic, enriched and motivic homotopy theory, NATO Science Series II: Mathematics, Physics and Chemistry, vol. 131 (Kluwer Academic Publishers, Dordrecht, 2004), 219–260.CrossRefGoogle Scholar
Morel, F., The stable ${\mathbb {A}}^1$-connectivity theorems, K-Theory 35 (2005), 1–68.10.1007/s10977-005-1562-7CrossRefGoogle Scholar
Morel, F., $\mathbb {A}^1$-algebraic topology, in International Congress of Mathematicians. Vol. II (European Mathematical Society, Zürich, 2006), 1035–1059.Google Scholar
Morel, F., Rational stable splitting of grassmannians and rational motivic sphere spectrum, Preprint (2006).Google Scholar
Morel, F., On the Friedlander-Milnor conjecture for groups of small rank, in Current developments in mathematics, 2010 (International Press, Somerville, MA, 2011), 45–93.Google Scholar
Morel, F., $\mathbb {A}^1$-algebraic topology over a field, Lecture Notes in Mathematics, vol. 2052 (Springer, Heidelberg, 2012).CrossRefGoogle Scholar
Morel, F. and Sawant, A., Cellular ${\mathbb {A}}^1$-homology and the motivic version of Matsumoto's theorem, Preprint (2020), arXiv:2007.14770.Google Scholar
Morel, F. and Voevodsky, V., ${\mathbf {A}}^1$-homotopy theory of schemes, Publ. Math. Inst. Hautes Études Sci. 90 (1999), 45–143.CrossRefGoogle Scholar
Panin, I. and Walter, C., Quaternionic Grassmannians and Pontryagin classes in algebraic geometry, Preprint (2010), arXiv:1011.0649.Google Scholar
Pushin, O., Higher Chern classes and Steenrod operations in motivic cohomology, K-Theory 31 (2004), 307–321.CrossRefGoogle Scholar
Quillen, D. G., Rational homotopy theory, Ann. of Math. (2) 90 (1969), 205–295.CrossRefGoogle Scholar
Riou, J., Algebraic $K$-theory, ${\bf A}^1$-homotopy and Riemann-Roch theorems, J. Topol. 3 (2010), 229–264.CrossRefGoogle Scholar
Schlichting, M. and Tripathi, G. S., Geometric models for higher Grothendieck-Witt groups in $\Bbb {A}^1$-homotopy theory, Math. Ann. 362 (2015), 1143–1167.10.1007/s00208-014-1154-zCrossRefGoogle Scholar
Serre, J.-P., Groupes d'homotopie et classes de groupes abéliens, Ann. of Math. (2) 58 (1953), 258–294.CrossRefGoogle Scholar
Strunk, F., On motivic spherical bundles. Thesis, Institut für Mathematik Universität Osnabrück (2012), available at https://repositorium.uni-osnabrueck.de/bitstream/urn:nbn:de:gbv:700-2013052710851/3/thesis_strunk.pdf.Google Scholar
Sullivan, D. P., Geometric topology: localization, periodicity and Galois symmetry, K-Monographs in Mathematics, vol. 8 (Springer, Dordrecht, 2005). The 1970 MIT notes, edited and with a preface by Andrew Ranicki.CrossRefGoogle Scholar
Suslin, A. A., Stably free modules, Mat. Sb. (N.S.) 102(144) (1977), 537–550.Google Scholar
Suslin, A. A., Mennicke symbols and their applications in the K-theory of fields, in Algebraic K-theory, Part I (Oberwolfach, 1980), Lecture Notes in Mathematics, vol. 966 (Springer, Berlin, 1982), 334–356.10.1007/BFb0062182CrossRefGoogle Scholar
Voelkel, K. and Wendt, M., On $\mathbb {A}^1$-fundamental groups of isotropic reductive groups, C. R. Math. Acad. Sci. Paris 354 (2016), 453–458.CrossRefGoogle Scholar
Voevodsky, V., Reduced power operations in motivic cohomology, Publ. Math. Inst. Hautes Études Sci. 98 (2003), 1–57.CrossRefGoogle Scholar
Voevodsky, V., Motivic Eilenberg-MacLane spaces, Publ. Math. Inst. Hautes Études Sci. 112 (2010), 1–99.10.1007/s10240-010-0024-9CrossRefGoogle Scholar
Whitehead, G. W., Elements of homotopy theory, Graduate Texts in Mathematics, vol. 61 (Springer, New York, 1978).10.1007/978-1-4612-6318-0CrossRefGoogle Scholar
Wickelgren, K. and Williams, T. B., The simplicial EHP sequence in ${\mathbb {A}}^1$-algebraic topology, Geom. Topol. 23 (2019), 1691–1777.CrossRefGoogle Scholar
Williams, B., The motivic cohomology of Stiefel varieties, J. K-Theory 10 (2012), 141–163.CrossRefGoogle Scholar