Article contents
Local-global principles in circle packings
Published online by Cambridge University Press: 20 May 2019
Abstract
We generalize work by Bourgain and Kontorovich [On the local-global conjecture for integral Apollonian gaskets, Invent. Math. 196 (2014), 589–650] and Zhang [On the local-global principle for integral Apollonian 3-circle packings, J. Reine Angew. Math. 737, (2018), 71–110], proving an almost local-to-global property for the curvatures of certain circle packings, to a large class of Kleinian groups. Specifically, we associate in a natural way an infinite family of integral packings of circles to any Kleinian group 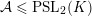 ${\mathcal{A}}\leqslant \text{PSL}_{2}(K)$ satisfying certain conditions, where
${\mathcal{A}}\leqslant \text{PSL}_{2}(K)$ satisfying certain conditions, where 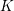 $K$ is an imaginary quadratic field, and show that the curvatures of the circles in any such packing satisfy an almost local-to-global principle. A key ingredient in the proof is that
$K$ is an imaginary quadratic field, and show that the curvatures of the circles in any such packing satisfy an almost local-to-global principle. A key ingredient in the proof is that 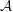 ${\mathcal{A}}$ possesses a spectral gap property, which we prove for any infinite-covolume, geometrically finite, Zariski dense Kleinian group in
${\mathcal{A}}$ possesses a spectral gap property, which we prove for any infinite-covolume, geometrically finite, Zariski dense Kleinian group in 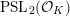 $\operatorname{PSL}_{2}({\mathcal{O}}_{K})$ containing a Zariski dense subgroup of
$\operatorname{PSL}_{2}({\mathcal{O}}_{K})$ containing a Zariski dense subgroup of 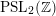 $\operatorname{PSL}_{2}(\mathbb{Z})$.
$\operatorname{PSL}_{2}(\mathbb{Z})$.
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
Fuchs has been supported by NSF DMS-1501970, the Sloan Foundation, and the BSF. Stange has been supported by NSF EAGER DMS-1643552 and NSF CAREER CNS-1652238.
References
- 8
- Cited by


