Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T23:10:21.014Z Has data issue: false hasContentIssue false
  • English
  • Français

The local structure theorem for real spherical varieties

Part of: Special varieties Noncompact transformation groups Algebraic groups

Published online by Cambridge University Press:  09 July 2015

Friedrich Knop ,
Bernhard Krötz  and
Henrik Schlichtkrull
Friedrich Knop
Affiliation:
FAU Erlangen-Nürnberg, Department Mathematik, Cauerstraße 11, D-91058 Erlangen, Germany email [email protected]
Bernhard Krötz
Affiliation:
Universität Paderborn, Institut für Mathematik, Warburger Straße 100, D-33098 Paderborn, Germany email [email protected]
Henrik Schlichtkrull
Affiliation:
University of Copenhagen, Department of Mathematics, Universitetsparken 5, DK-2100 Copenhagen Ø, Denmark email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

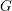Let $G$ be an algebraic real reductive group and 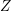$Z$ a real spherical 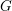$G$-variety, that is, it admits an open orbit for a minimal parabolic subgroup 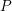$P$. We prove a local structure theorem for 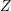$Z$. In the simplest case where 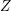$Z$ is homogeneous, the theorem provides an isomorphism of the open 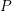$P$-orbit with a bundle 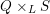$Q\times _{L}S$. Here 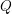$Q$ is a parabolic subgroup with Levi decomposition 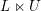$L\ltimes U$, and 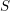$S$ is a homogeneous space for a quotient 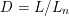$D=L/L_{n}$ of 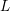$L$, where 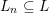$L_{n}\subseteq L$ is normal, such that 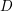$D$ is compact modulo center.

Keywords

spherical varietieshomogeneous spacesreal reductive groups

MSC classification

Primary: 14L30: Group actions on varieties or schemes (quotients) 14M17: Homogeneous spaces and generalizations 14M27: Compactifications; symmetric and spherical varieties 22F30: Homogeneous spaces
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 11 , November 2015 , pp. 2145 - 2159
Copyright
© The Authors 2015 

References

Borel, A., Linear algebraic groups (Springer, 1991).CrossRefGoogle Scholar
Brion, M., Variétés Sphériques, Notes de la session de la SMF, ‘Opérations hamiltoniennes et opérations de groupes algébriques’ (Grenoble, 1997), www-fourier.ujf-grenoble.fr/∼mbrion/spheriques.pdf.Google Scholar
Brion, M., Luna, D. and Vust, T., Espaces homogénes sphériques, Invent. Math. 84 (1986), 617–632.CrossRefGoogle Scholar
Knop, F., The asymptotic behavior of invariant collective motion, Invent. Math. 116 (1994), 309–328.CrossRefGoogle Scholar
Knop, F., Kraft, H., Luna, D. and Vust, T., Local properties of algebraic group actions, in Algebraische Transformationsgruppen und Invariantentheorie, DMV Seminar, vol. 13 (Birkhäuser, Basel, 1989), 63–75.CrossRefGoogle Scholar
Krämer, M., Sphärische Untergruppen in kompakten zusammenhängenden Gruppen, Compositio Math. 38 (1979), 129–153.Google Scholar
Krötz, B. and Schlichtkrull, H., Finite orbit decomposition of real flag manifolds, J. Eur. Math. Soc. (JEMS), to appear, arXiv:1307.2375.Google Scholar
Springer, T. A., Aktionen reduktiver Gruppen auf Varietäten, in Algebraische Transformationsgruppen und Invariantentheorie, DMV Seminar, vol. 13 (Birkhäuser, Basel, 1989), 3–39.CrossRefGoogle Scholar
Vinberg, E. and Kimel’feld, B., Homogeneous domains on flag manifolds and spherical subsets of semisimple Lie groups, Funktsional. Anal. i Prilozhen. 12 (1978), 12–19.CrossRefGoogle Scholar