Published online by Cambridge University Press: 27 August 2014
Let 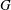 $G$ and
$G$ and 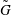 $\tilde{G}$ be Kleinian groups whose limit sets
$\tilde{G}$ be Kleinian groups whose limit sets 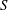 $S$ and
$S$ and 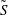 $\tilde{S}$, respectively, are homeomorphic to the standard Sierpiński carpet, and such that every complementary component of each of
$\tilde{S}$, respectively, are homeomorphic to the standard Sierpiński carpet, and such that every complementary component of each of 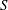 $S$ and
$S$ and 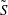 $\tilde{S}$ is a round disc. We assume that the groups
$\tilde{S}$ is a round disc. We assume that the groups  $G$ and
$G$ and  $\tilde{G}$ act cocompactly on triples on their respective limit sets. The main theorem of the paper states that any quasiregular map (in a suitably defined sense) from an open connected subset of
$\tilde{G}$ act cocompactly on triples on their respective limit sets. The main theorem of the paper states that any quasiregular map (in a suitably defined sense) from an open connected subset of 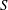 $S$ to
$S$ to 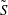 $\tilde{S}$ is the restriction of a Möbius transformation that takes
$\tilde{S}$ is the restriction of a Möbius transformation that takes 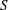 $S$ onto
$S$ onto 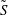 $\tilde{S}$, in particular it has no branching. This theorem applies to the fundamental groups of compact hyperbolic 3-manifolds with non-empty totally geodesic boundaries. One consequence of the main theorem is the following result. Assume that
$\tilde{S}$, in particular it has no branching. This theorem applies to the fundamental groups of compact hyperbolic 3-manifolds with non-empty totally geodesic boundaries. One consequence of the main theorem is the following result. Assume that 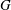 $G$ is a torsion-free hyperbolic group whose boundary at infinity
$G$ is a torsion-free hyperbolic group whose boundary at infinity 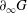 $\partial _{\infty }G$ is a Sierpiński carpet that embeds quasisymmetrically into the standard 2-sphere. Then there exists a group
$\partial _{\infty }G$ is a Sierpiński carpet that embeds quasisymmetrically into the standard 2-sphere. Then there exists a group 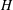 $H$ that contains
$H$ that contains 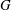 $G$ as a finite index subgroup and such that any quasisymmetric map
$G$ as a finite index subgroup and such that any quasisymmetric map 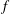 $f$ between open connected subsets of
$f$ between open connected subsets of 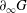 $\partial _{\infty }G$ is the restriction of the induced boundary map of an element
$\partial _{\infty }G$ is the restriction of the induced boundary map of an element 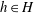 $h\in H$.
$h\in H$.