Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-27T21:20:03.248Z Has data issue: false hasContentIssue false
  • English
  • Français

Local models for Weil-restricted groups

Part of: Special varieties Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  27 September 2016

Brandon Levin
Brandon Levin*
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Avenue, Room 208C, Chicago, IL 60637, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

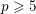We extend the group-theoretic construction of local models of Pappas and Zhu [Local models of Shimura varieties and a conjecture of Kottwitz, Invent. Math. 194 (2013), 147–254] to the case of groups obtained by Weil restriction along a possibly wildly ramified extension. This completes the construction of local models for all reductive groups when $p\geqslant 5$. We show that the local models are normal with special fiber reduced and study the monodromy action on the sheaves of nearby cycles. As a consequence, we prove a conjecture of Kottwitz that the semi-simple trace of Frobenius gives a central function in the parahoric Hecke algebra. We also introduce a notion of splitting model and use this to study the inertial action in the case of an unramified group.

Keywords

algebraic groupsaffine Grassmanniansnearby cyclesShimura varieties

MSC classification

Primary: 14G35: Modular and Shimura varieties
Secondary: 11G18: Arithmetic aspects of modular and Shimura varieties 14M15: Grassmannians, Schubert varieties, flag manifolds
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 12 , December 2016 , pp. 2563 - 2601
Copyright
© The Author 2016 

References

Beilinson, A. and Drinfeld, V., Quantization of Hitchin’s integrable system and Hecke eigensheaves, Preprint, http://www.math.utexas.edu/users/benzvi/BD/hitchin.pdf.Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models (Springer, New York, 1990).CrossRefGoogle Scholar
Bruhat, F. and Tits, J., Groupes réductifs sure un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée , Publ. Math. Inst. Hautes Études Sci. 60 (1984), 197–376.Google Scholar
Edixhoven, B., Néron models and tame ramification , Compositio Math. 81 (1992), 291–306.Google Scholar
Faltings, G., Algebraic loop groups and moduli spaces of bundles , J. Eur. Math. Soc. 5 (2003), 41–68.Google Scholar
Fourier, G. and Littelmann, P., Tensor product structure of affine Demazure modules and limit constructions , Nagoya Math. J. 182 (2006), 171–198.Google Scholar
Gaitsgory, D., Construction of central elements in the affine Hecke algebra via nearby cycles , Invent. Math. 144 (2001), 253–280.Google Scholar
Görtz, U. and Haines, T., The Jordan-Hölder series for nearby cycles on some Shimura vareities and affine flag varieties , J. Reine Angew. Math. 609 (2007), 161–213.Google Scholar
Haines, T. and Ngô, B., Nearby cycles for local models of some Shimura varieties , Compositio Math. 133 (2002), 117–150.Google Scholar
Haines, T. and Rapoport, M., On parahoric subgroups , Adv. Math. 219 (2008), 188–198.Google Scholar
He, X., Normality and Cohen–Macaulayness of local models of Shimura varieties , Duke Math. J. 162 (2013), 2509–2523.Google Scholar
Kottwitz, R., Isocrystals with additional structure II , Compositio Math. 109 (1997), 255–339.CrossRefGoogle Scholar
Levin, B., $G$ -valued flat deformations and local models, PhD thesis, Stanford University (2013), available at http://math.uchicago.edu/∼bwlevin/LevinThesis.pdf.Google Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings , Ann. of Math. (2) 166 (2007), 95–143.CrossRefGoogle Scholar
Pappas, G. and Rapoport, M., Local models in the ramified case. I. The EL-case , J. Algebraic Geom. 12 (2003), 107–145.CrossRefGoogle Scholar
Pappas, G. and Rapoport, M., Local models in the ramified case. II. Splitting models , Duke Math. J. 127 (2005), 193–250.Google Scholar
Pappas, G. and Rapoport, M., Twisted loop groups and their affine flag varieties , Adv. Math. 219 (2008), 118–198.Google Scholar
Pappas, G., Rapoport, M. and Smithling, B., Local models of Shimura varieties, I. Geometry and combinatorics , in Handbook of moduli, Vol. III, Advanced Lectures in Mathematics, vol. 26 (International Press, Somerville, MA, 2013), 135–217.Google Scholar
Pappas, G. and Zhu, X., Local models of Shimura varieties and a conjecture of Kottwitz , Invent. Math. 194 (2013), 147–254.CrossRefGoogle Scholar
Prasad, G., Galois-fixed points in the Bruhat–Tits building of a reductive group , Bull. Soc. Math. France 129 (2001), 169–174.CrossRefGoogle Scholar
Rapoport, M. and Zink, T., Period spaces for p-divisible groups, Annals of Mathematics Studies, vol. 144 (Princeton University Press, Princeton, NJ, 1996).CrossRefGoogle Scholar
Richarz, T., Affine Grassmannians and geometric Satake equivalences , Int. Math. Res. Not. IMRN 2016 (2016), 3717–3767.Google Scholar
Seshadri, C. S., Triviality of vector bundles over the affine space K 2 , Proc. Natl. Acad. Sci. USA 44 (1958), 456–458.Google Scholar
Yu, J.-K., Smooth models associated to concave functions in Bruhat–Tits theory, Preprint, available at http://www.math.purdue.edu/∼jyu/prep/model.pdf.Google Scholar
Zhu, X., Affine Demazure modules and T-fixed point subschemes in the affine Grassmannian , Adv. Math. 221 (2009), 570–600.Google Scholar
Zhu, X., On the coherence conjecture of Pappas and Rapoport , Ann. of Math. (2) 180 (2014), 1–85.Google Scholar
Zhu, X., The geometric Satake correspondence for ramified groups , Ann. Sci. Éc. Norm. Supér. (4) 48 (2015), 409–451.CrossRefGoogle Scholar