Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Iliev, Plamen
2012.
Meixner polynomials in several variables satisfying bispectral difference equations.
Advances in Applied Mathematics,
Vol. 49,
Issue. 1,
p.
15.
Genest, Vincent X
Vinet, Luc
and
Zhedanov, Alexei
2013.
The multivariate Krawtchouk polynomials as matrix elements of the rotation group representations on oscillator states.
Journal of Physics A: Mathematical and Theoretical,
Vol. 46,
Issue. 50,
p.
505203.
Griffiths, Robert
2016.
Multivariate Krawtchouk Polynomials and Composition Birth and Death Processes.
Symmetry,
Vol. 8,
Issue. 5,
p.
33.
Griffiths, Robert
2016.
Lancaster distributions and Markov chains with multivariate Poisson–Charlier, Meixner and Hermite–Chebycheff polynomial eigenfunctions.
Journal of Approximation Theory,
Vol. 207,
Issue. ,
p.
139.
Morales, John Vincent S.
2016.
On Lee association schemes over Z4 and their Terwilliger algebra.
Linear Algebra and its Applications,
Vol. 510,
Issue. ,
p.
311.
Iliev, Plamen
2017.
The generic quantum superintegrable system on the sphere and Racah operators.
Letters in Mathematical Physics,
Vol. 107,
Issue. 11,
p.
2029.
Iliev, Plamen
and
Xu, Yuan
2017.
Connection coefficients for classical orthogonal polynomials of several variables.
Advances in Mathematics,
Vol. 310,
Issue. ,
p.
290.
Morales, John Vincent S.
and
Tanaka, Hajime
2018.
An Assmus–Mattson theorem for codes over commutative association schemes.
Designs, Codes and Cryptography,
Vol. 86,
Issue. 5,
p.
1039.
Diaconis, Persi
and
Griffiths, Robert C.
2019.
Reproducing kernel orthogonal polynomials on the multinomial distribution.
Journal of Approximation Theory,
Vol. 242,
Issue. ,
p.
1.
Bergeron, G.
Koelink, E.
and
Vinet, L.
2019.
SU
q
(3) corepresentations and bivariate q-Krawtchouk polynomials.
Journal of Mathematical Physics,
Vol. 60,
Issue. 5,
Iliev, Plamen
and
Xu, Yuan
2020.
Hahn polynomials on polyhedra and quantum integrability.
Advances in Mathematics,
Vol. 364,
Issue. ,
p.
107032.
Crampé, Nicolas
van de Vijver, Wouter
and
Vinet, Luc
2020.
Racah Problems for the Oscillator Algebra, the Lie Algebra $$\mathfrak {sl}_n$$, and Multivariate Krawtchouk Polynomials.
Annales Henri Poincaré,
Vol. 21,
Issue. 12,
p.
3939.
De Bie, Hendrik
and
De Clercq, Hadewijch
2021.
The q‐Bannai–Ito algebra and multivariate (−q)‐Racah and Bannai–Ito polynomials.
Journal of the London Mathematical Society,
Vol. 103,
Issue. 1,
p.
71.
Kawamura, Koei
2021.
Infinite-Variate Extensions of Krawtchouk Polynomials and Zonal Spherical Functions over a Local Field.
Funkcialaj Ekvacioj,
Vol. 64,
Issue. 1,
p.
75.
van Diejen, J.F.
2022.
Harmonic analysis of boxed hyperoctahedral Hall-Littlewood polynomials.
Journal of Functional Analysis,
Vol. 282,
Issue. 1,
p.
109256.
Bernard, Pierre-Antoine
Crampé, Nicolas
Nepomechie, Rafael I.
Parez, Gilles
Poulain d'Andecy, Loïc
and
Vinet, Luc
2022.
Entanglement of inhomogeneous free fermions on hyperplane lattices.
Nuclear Physics B,
Vol. 984,
Issue. ,
p.
115975.
Groenevelt, Wolter
and
Koelink, Erik
2023.
Orthogonal functions related to Lax pairs in Lie algebras.
The Ramanujan Journal,
Vol. 61,
Issue. 2,
p.
445.
Miki, Hiroshi
Tsujimoto, Satoshi
and
Zhao, Da
2023.
Quantum walks on simplexes and multiple perfect state transfer.
Journal of Physics A: Mathematical and Theoretical,
Vol. 56,
Issue. 46,
p.
465201.
Crampé, Nicolas
Gaboriaud, Julien
Poulain d’Andecy, Loïc
and
Vinet, Luc
2023.
Matrix elements of SO(3) in sl3 representations as bispectral multivariate functions.
Journal of Mathematical Physics,
Vol. 64,
Issue. 11,
Iliev, Plamen
2024.
Gaudin Model for the Multinomial Distribution.
Annales Henri Poincaré,
Vol. 25,
Issue. 3,
p.
1795.
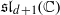 . Our approach yields yet another proof of the orthogonality. It also shows that the polynomials satisfy d independent recurrence relations each involving d2+d+1 terms. This, combined with the duality, establishes their bispectrality. We illustrate our results with several explicit examples.
. Our approach yields yet another proof of the orthogonality. It also shows that the polynomials satisfy d independent recurrence relations each involving d2+d+1 terms. This, combined with the duality, establishes their bispectrality. We illustrate our results with several explicit examples.

