Article contents
Le principe de Hasse pour les espaces homogènes : réduction au cas des stabilisateurs finis
Published online by Cambridge University Press: 04 July 2019
Abstract
Nous montrons, pour une grande famille de propriétés des espaces homogènes, qu’une telle propriété vaut pour tout espace homogène d’un groupe linéaire connexe dès qu’elle vaut pour les espaces homogènes de 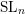 $\text{SL}_{n}$ à stabilisateur fini. Nous réduisons notamment à ce cas particulier la vérification d’une importante conjecture de Colliot-Thélène sur l’obstruction de Brauer–Manin au principe de Hasse et à l’approximation faible. Des travaux récents de Harpaz et Wittenberg montrent que le résultat principal s’applique également à la conjecture analogue (dite conjecture (E)) pour les zéro-cycles.
$\text{SL}_{n}$ à stabilisateur fini. Nous réduisons notamment à ce cas particulier la vérification d’une importante conjecture de Colliot-Thélène sur l’obstruction de Brauer–Manin au principe de Hasse et à l’approximation faible. Des travaux récents de Harpaz et Wittenberg montrent que le résultat principal s’applique également à la conjecture analogue (dite conjecture (E)) pour les zéro-cycles.
For a large family of properties of homogeneous spaces, we prove that such a property holds for all homogeneous spaces of connected linear algebraic groups as soon as it holds for homogeneous spaces of 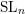 $\text{SL}_{n}$ with finite stabilisers. As an example, we reduce to this particular case an important conjecture by Colliot-Thélène about the Brauer–Manin obstruction to the Hasse principle and to weak approximation. A recent work by Harpaz and Wittenberg proves that the main result also applies to the analogous conjecture (known as conjecture (E)) for zero-cycles on homogeneous spaces.
$\text{SL}_{n}$ with finite stabilisers. As an example, we reduce to this particular case an important conjecture by Colliot-Thélène about the Brauer–Manin obstruction to the Hasse principle and to weak approximation. A recent work by Harpaz and Wittenberg proves that the main result also applies to the analogous conjecture (known as conjecture (E)) for zero-cycles on homogeneous spaces.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
References
- 9
- Cited by


