No CrossRef data available.
Article contents
Kirillov’s orbit method and polynomiality of the faithful dimension of 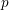 $p$-groups
$p$-groups
Published online by Cambridge University Press: 11 July 2019
Abstract
Given a finite group 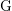 $\text{G}$ and a field
$\text{G}$ and a field 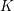 $K$, the faithful dimension of
$K$, the faithful dimension of 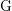 $\text{G}$ over
$\text{G}$ over 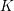 $K$ is defined to be the smallest integer
$K$ is defined to be the smallest integer  $n$ such that
$n$ such that 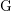 $\text{G}$ embeds into
$\text{G}$ embeds into 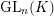 $\operatorname{GL}_{n}(K)$. We address the problem of determining the faithful dimension of a
$\operatorname{GL}_{n}(K)$. We address the problem of determining the faithful dimension of a 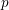 $p$-group of the form
$p$-group of the form 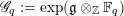 $\mathscr{G}_{q}:=\exp (\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$ associated to
$\mathscr{G}_{q}:=\exp (\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$ associated to 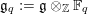 $\mathfrak{g}_{q}:=\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q}$ in the Lazard correspondence, where
$\mathfrak{g}_{q}:=\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q}$ in the Lazard correspondence, where 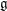 $\mathfrak{g}$ is a nilpotent
$\mathfrak{g}$ is a nilpotent 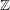 $\mathbb{Z}$-Lie algebra which is finitely generated as an abelian group. We show that in general the faithful dimension of
$\mathbb{Z}$-Lie algebra which is finitely generated as an abelian group. We show that in general the faithful dimension of 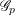 $\mathscr{G}_{p}$ is a piecewise polynomial function of
$\mathscr{G}_{p}$ is a piecewise polynomial function of 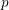 $p$ on a partition of primes into Frobenius sets. Furthermore, we prove that for
$p$ on a partition of primes into Frobenius sets. Furthermore, we prove that for 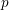 $p$ sufficiently large, there exists a partition of
$p$ sufficiently large, there exists a partition of 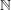 $\mathbb{N}$ by sets from the Boolean algebra generated by arithmetic progressions, such that on each part the faithful dimension of
$\mathbb{N}$ by sets from the Boolean algebra generated by arithmetic progressions, such that on each part the faithful dimension of 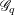 $\mathscr{G}_{q}$ for
$\mathscr{G}_{q}$ for 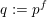 $q:=p^{f}$ is equal to
$q:=p^{f}$ is equal to 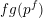 $fg(p^{f})$ for a polynomial
$fg(p^{f})$ for a polynomial 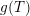 $g(T)$. We show that for many naturally arising
$g(T)$. We show that for many naturally arising 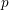 $p$-groups, including a vast class of groups defined by partial orders, the faithful dimension is given by a single formula of the latter form. The arguments rely on various tools from number theory, model theory, combinatorics and Lie theory.
$p$-groups, including a vast class of groups defined by partial orders, the faithful dimension is given by a single formula of the latter form. The arguments rely on various tools from number theory, model theory, combinatorics and Lie theory.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2019
Footnotes
Throughout the preparation of this paper, M.B. was supported by Emmanuel Breuillard’s ERC grant ‘GeTeMo’, K.M.-K. was partially supported by the DFG grant DI506/14-1, and H.S. was supported by NSERC Discovery Grants RGPIN-2013-355464 and RGPIN-2018-04044.
References
- 24
- Cited by


