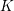Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T10:53:19.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariants and $K$-spectrums of local theta lifts

Part of: Lie groups

Published online by Cambridge University Press:  17 September 2014

Hung Yean Loke  and
Jiajun Ma
Hung Yean Loke
Affiliation:
Department of Mathematics, National University of Singapore, Block S17, 10, Lower Kent Ridge Road, Singapore 119076, Singapore email [email protected]
Jiajun Ma
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, P.O.B. 653, Be’er Sheva 84105, Israel email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 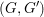$(G,G^{\prime })$ be a type I irreducible reductive dual pair in Sp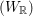$(W_{\mathbb{R}})$. We assume that 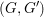$(G,G^{\prime })$ is in the stable range where 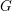$G$ is the smaller member. Let 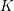$K$ and $K^{\prime }$ be maximal compact subgroups of 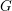$G$ and 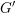$G^{\prime }$ respectively. 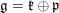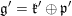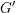Let $\mathfrak{g}=\mathfrak{k}\bigoplus \mathfrak{p}$ and $\mathfrak{g}^{\prime }=\mathfrak{k}^{\prime }\bigoplus \mathfrak{p}^{\prime }$ be the complexified Cartan decompositions of the Lie algebras of $G$ and $G^{\prime }$ respectively. Let 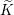$\widetilde{K}$ and 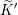$\widetilde{K}^{\prime }$ be the inverse images of 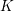$K$ and 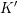$K^{\prime }$ in the metaplectic double cover 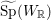$\widetilde{\text{Sp}}(W_{\mathbb{R}})$ of Sp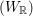$(W_{\mathbb{R}})$. Let 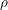${\it\rho}$ be a genuine irreducible 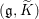$(\mathfrak{g},\widetilde{K})$-module. Our first main result is that if 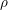${\it\rho}$ is unitarizable, then except for one special case, the full local theta lift 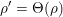${\it\rho}^{\prime }={\rm\Theta}({\it\rho})$ is equal to the local theta lift 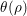${\it\theta}({\it\rho})$. Thus excluding the special case, the full theta lift 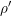${\it\rho}^{\prime }$ is an irreducible and unitarizable 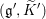$(\mathfrak{g}^{\prime },\widetilde{K}^{\prime })$-module. Our second main result is that the associated variety and the associated cycle of 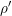${\it\rho}^{\prime }$ are the theta lifts of the associated variety and the associated cycle of the contragredient representation 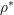${\it\rho}^{\ast }$ respectively. Finally we obtain some interesting 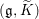$(\mathfrak{g},\widetilde{K})$-modules whose 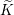$\widetilde{K}$-spectrums are isomorphic to the spaces of global sections of some vector bundles on some nilpotent 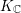$K_{\mathbb{C}}$-orbits in 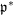$\mathfrak{p}^{\ast }$.

Keywords

local theta liftsnilpotent orbitsassociated varietiesassociated cyclesmoment maps

MSC classification

Primary: 22E46: Semisimple Lie groups and their representations 22E47: Representations of Lie and real algebraic groups
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 1 , January 2015 , pp. 179 - 206
Copyright
© The Author(s) 2014 

References

Adams, J., The real Chevalley involution, Preprint (2012), available at arXiv:1203.1901.Google Scholar
Bernstein, J., Modules over the ring of differential operators; the study of fundamental solutions of equations with constant coefficients, Funct. Anal. Appl. 5 (1972), 1–16.Google Scholar
Brylinski, R., Dixmier Algebras for classical complex nilpotent orbits via Kraft-Procesi models I, in The orbit method in geometry and physics: in honor of A.A. Kirillov (Birkhäuser, Basel, 2003).Google Scholar
Cline, E., Parshall, B. and Scott, L., A Mackey imprimitivity theory for algebraic groups, Math. Z. 182 (1983), 447–471.Google Scholar
Daszkiewicz, A., Kraśkiewicz, W. and Przebinda, T., Dual pairs and Kostant–Sekiguchi correspondence. I, J. Algebra 250 (2002), 408–426.CrossRefGoogle Scholar
Daszkiewicz, A., Kraśkiewicz, W. and Przebinda, T., Dual pairs and Kostant–Sekiguchi correspondence. II. Classification of nilpotent elements, Cent. Eur. J. Math. 3 (2005), 430–474.Google Scholar
Debarre, O. and Tuong, T.-T., Representations of S O (k, ℂ) on harmonic polynomials on a null cone, Proc. Amer. Math. Soc. 112 (1991), 31–44.Google Scholar
Enright, T. J., Howe, R. and Wallach, N. R., A classification of unitary highest weight modules, in Representation theory of reductive groups (Park City, Utah, 1982), Progress in Mathematics, vol. 40 (Birkhäuser, Boston, MA, 1983), 97–147.CrossRefGoogle Scholar
Gomez, R. and Zhu, C.-b., Theta lifting of generalized Whittaker models associated to nilpotent orbits, Geom. Funct. Anal. 24 (2014), 796–853.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné) IV: Étude locale des schémas et des morphismes de schémas (Troisième partie), Publ. Math. Inst. Hautes Études Sci. 28 (1966).Google Scholar
Hartshorne, R., Local cohomology: a seminar given by A. Grothendieck, Harvard University, Fall 1961, Lecture Notes in Mathematics, vol. 41 (Springer, Berlin, 1967).Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1983).Google Scholar
He, H., Theta correspondence in semistable range I: Construction and irreducibility, Commun. Contemp. Math. 2 (2000), 255–283.Google Scholar
Howe, R., Reciprocity laws in the theory of dual pairs, in Representation theory of reductive groups (Park City, Utah, 1982), Progress in Mathematics, vol. 40 (Birkhäuser, Boston, MA, 1983), 159–175.Google Scholar
Howe, R., Transcending classical invariant theory, J. Amer. Math. Soc. 2 (1989), 535–552.Google Scholar
Howe, R., Perspectives on invariant theory: Schur duality, multiplicity-free actions and beyond, in The Schur lectures (1992), Israel Mathematical Conference Proceedings, vol. 8, eds Piatetski-Shapiro, I. et al. (Bar-Ilan University, Ramat-Gan, 1995), 1–182.Google Scholar
Jakobsen, H. P. and Vergne, M., Restrictions and expansions of holomorphic representations, J. Funct. Anal. 34 (1979), 29–53.CrossRefGoogle Scholar
Kashiwara, M. and Vergne, M., On the Segal–Shale–Weil representations and harmonic polynomials, Invent. Math. 44(1) (1978), 1–47.CrossRefGoogle Scholar
Kostant, B., Lie group representations on polynomial rings, Amer. J. Math. 85 (1963), 327–404.Google Scholar
Kraft, H. and Procesi, C., On the geometry of conjugacy classes in classical groups, Comment. Math. Helv. 57 (1982), 539–602.Google Scholar
Li, J.-S., Singular unitary representations of classical groups, Invent. Math. 97 (1989), 237–255.Google Scholar
Lin, Y., Sun, B. and Tan, S., MVW-extensions of quaternionic classical groups, Math. Z. (2013), 1–9; doi: 10.1007/s00209-013-1246-6.Google Scholar
Loke, H. Y., Howe quotients of unitary characters and unitary lowest weight modules. With an appendix by S. T. Lee, Represent. Theory 10 (2006), 21–47.CrossRefGoogle Scholar
Loke, H. Y., Ma, J.-J. and Tang, U.-L., Associated cycles of local theta lifts of unitary characters and unitary lowest weight modules, Preprint (2012); arXiv:1207.6451.Google Scholar
Ma, J.-J., Two topics in local theta correspondence, PhD thesis, National University of Singapore (2012).Google Scholar
Moeglin, C., Vigneras, M. F. and Waldspurger, J. L., Correspondances de Howe sur un corps p-adique, Lecture Notes in Mathematics, vol. 1291 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Moeglin, C. and Waldspurger, J. L., Modèles de Whittaker dégénéres pour des groupes p-adiques, (Degenerate Whittaker models of p-adic groups), Math. Z. 196 (1987), 427–452 (French).CrossRefGoogle Scholar
Nishiyama, K., Ochiai, H. and Taniguchi, K., Bernstein degree and associated cycles of Harish-Chandra modules-Hermitian symmetric case, Astérisque 273 (2001), 13–80.Google Scholar
Nishiyama, K., Ochiai, H. and Zhu, C.-B., Theta lifting of nilpotent orbits for symmetric pairs, Trans. Amer. Math. Soc. 358 (2006), 2713–2734.Google Scholar
Nishiyama, K. and Zhu, C.-B., Theta lifting of unitary lowest weight modules and their associated cycles, Duke Math. J. 125 (2004), 415–465.Google Scholar
Ohta, T., The closure of nilpotent orbits in the classical symmetric pairs and their singularities, Tohoku Math. J. (2) 43 (1991), 161–211.Google Scholar
Popov, V. L. and Vinberg, E. B., Invariant theory, in Algebraic geometry IV: linear algebraic groups, invariant theory, Encyclopaedia of Mathematical Sciences, vol. 55 (Springer, New York, 1994).Google Scholar
Protsak, V. and Przebinda, T., On the occurrence of admissible representations in the real Howe correspondence in stable range, Manuscripta Math. 126 (2008), 135–141.Google Scholar
Przebinda, T., Characters, dual pairs, and unitary representations, Duke Math. J. 69 (1993), 547–592.Google Scholar
Sun, B., A note on MVW-involutions, in Fifth International Congress of Chinese Mathematicians (American Mathematical Society and International Press, Cambridge, MA, 2012), 305–314.Google Scholar
Vogan , D. A. Jr., Associated varieties and unipotent representations, in Proc. Bowdoin conf. on harmonic analysis, Progress in Mathematics, vol. 101, eds Barker, W. and Sally, P. (Birkhäuser, Boston, 1991).Google Scholar
Weyl, H., The classical groups: their invariants and representations, Princeton Landmarks in Mathematics, vol. 1 (Princeton University Press, Princeton, NJ, 1997).Google Scholar
Yamashita, H., Cayley transform and generalized Whittaker models for irreducible highest weight modules, Astérisque 273 (2001), 81–138.Google Scholar
Yang, L., On quantization of spherical nilpotent orbits of $\mathfrak{g}$-height 2, PhD Thesis, HKUST (2010).Google Scholar
Yang, L., On the quantization of spherical nilpotent orbits, Trans. Amer. Math. Soc. 365 (2013), 6499–6515.CrossRefGoogle Scholar