Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T23:23:00.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Identities for field extensions generalizing the Ohno–Nakagawa relations

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  30 June 2015

Henri Cohen ,
Simon Rubinstein-Salzedo  and
Frank Thorne
Henri Cohen
Affiliation:
Université de Bordeaux, Institut de Mathématiques, UMR 5251 du CNRS, 351 Cours de la Libération, 33405 Talence Cedex, France email [email protected]
Simon Rubinstein-Salzedo
Affiliation:
Department of Statistics, Stanford University, 390 Serra Mall, Stanford, CA 94305, USA email [email protected]
Frank Thorne
Affiliation:
Department of Mathematics, University of South Carolina, 1523 Greene Street, Columbia, SC 29208, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In previous work, Ohno conjectured, and Nakagawa proved, relations between the counting functions of certain cubic fields. These relations may be viewed as complements to the Scholz reflection principle, and Ohno and Nakagawa deduced them as consequences of ‘extra functional equations’ involving the Shintani zeta functions associated to the prehomogeneous vector space of binary cubic forms. In the present paper, we generalize their result by proving a similar identity relating certain degree-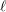$\ell$ fields to Galois groups 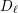$D_{\ell }$ and 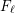$F_{\ell }$, respectively, for any odd prime $\ell$; in particular, we give another proof of the Ohno–Nakagawa relation without appealing to binary cubic forms.

Keywords

Ohno–Nakagawa relationsScholz reflectionfield extensions

MSC classification

Primary: 11R21: Other number fields
Secondary: 11R29: Class numbers, class groups, discriminants
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 11 , November 2015 , pp. 2059 - 2075
Copyright
© The Authors 2015 

References

Bhargava, M., Higher composition laws. III. The parametrization of quartic rings, Ann. of Math. (2) 159 (2004), 1329–1360.CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quartic rings and fields, Ann. of Math. (2) 162 (2005), 1031–1063.CrossRefGoogle Scholar
Cohen, H., Advanced topics in computational number theory, Graduate Texts in Mathematics, vol. 193 (Springer, New York, 2000).CrossRefGoogle Scholar
Cohen, H., Counting A 4 and S 4 number fields with given resolvent cubic, in High primes and misdemeanours: lectures in honour of the 60th birthday of Hugh Cowie Williams, Fields Institute Communications, vol. 41 (American Mathematical Society, Providence, RI, 2004), 159–168.Google Scholar
Cohen, H., Diaz y Diaz, F. and Olivier, M., On the density of discriminants of cyclic extensions of prime degree, J. Reine Angew. Math. 550 (2002), 169–209.Google Scholar
Cohen, H., Diaz y Diaz, F. and Olivier, M., Cyclotomic extensions of number fields, Indag. Math. (N.S.) 14 (2003), 183–196.CrossRefGoogle Scholar
Cohen, H., Diaz y Diaz, F. and Olivier, M., Counting discriminants of number fields, J. Théor. Nombres Bordeaux 18 (2006), 573–593.CrossRefGoogle Scholar
Cohen, H. and Morra, A., Counting cubic extensions with given quadratic resolvent, J. Algebra 325 (2011), 461–478.CrossRefGoogle Scholar
Cohen, H. and Thorne, F., Dirichlet series associated to quartic fields with given resolvent, Preprint (2013), arXiv:1302.5728.Google Scholar
Cohen, H. and Thorne, F., On $D_{\ell }$-extensions of odd prime degree $\ell$, Preprint (2013).Google Scholar
Cohen, H. and Thorne, F., Dirichlet series associated to cubic fields with given quadratic resolvent, Michigan Math. J. 63 (2014), 253–273.CrossRefGoogle Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat’s last theorem, in Elliptic curves, modular forms & Fermat’s last theorem (Hong Kong, 1993) (International Press, Cambridge, MA, 1997), 2–140.Google Scholar
Fröhlich, A. and Taylor, M. J., Algebraic number theory, Cambridge Studies in Advanced Mathematics, vol. 27 (Cambridge University Press, Cambridge, 1993).Google Scholar
Greenberg, R., Iwasawa theory for p-adic representations, in Algebraic number theory, Advanced Studies in Pure Mathematics, vol. 17 (Academic Press, Boston, MA, 1989), 97–137.Google Scholar
Jones, J. and Roberts, D., Number fields (2013), http://hobbes.la.asu.edu/NFDB/.Google Scholar
Kaplan, N., Marcinek, J. and Takloo-Bighash, R., Counting subrings of $\mathbb{Z}^{n}$ of finite index. Preprint (2013), arXiv:1008.2053.Google Scholar
Lang, S., Algebraic number theory, Graduate Texts in Mathematics, vol. 110, 2nd edition (Springer, New York, 1994).CrossRefGoogle Scholar
Nakagawa, J., Orders of a quartic field, Mem. Amer. Math. Soc. 122 (1996), viii+75.Google Scholar
Nakagawa, J., On the relations among the class numbers of binary cubic forms, Invent. Math. 134 (1998), 101–138.CrossRefGoogle Scholar
Ohno, Y., A conjecture on coincidence among the zeta functions associated with the space of binary cubic forms, Amer. J. Math. 119 (1997), 1083–1094.CrossRefGoogle Scholar
PARI Group, Bordeaux. PARI/GP, version 2.6.2 (tested using version 2.5.1), 2014. Available from http://pari.math.u-bordeaux.fr/.Google Scholar
Poitou, G., Cohomologie galoisienne des modules finis, Séminaire de l’Institut de Mathématiques de Lille, vol. 13 (Dunod, Paris, 1967).Google Scholar
Scholz, A., Über die Beziehung der Klassenzahlen quadratischer Körper zueinander, J. Reine Angew. Math. 166 (1932), 201–203.CrossRefGoogle Scholar
Serre, J.-P., Local class field theory, in Algebraic number theory (Proceedings of an instructional conference, Brighton, 1965) (Thompson, Washington, DC, 1967), 128–161.Google Scholar
Tate, J., Duality theorems in Galois cohomology over number fields, in Proceedings of the International Congress of Mathematicians (Stockholm, 1962) (Mittag-Leffler Institute, Djursholm, 1963), 288–295.Google Scholar
Washington, L. C., Introduction to cyclotomic fields, Graduate Texts in Mathematics, vol. 83, 2nd edition (Springer, New York, 1997).CrossRefGoogle Scholar
Wiles, A., Modular elliptic curves and Fermat’s last theorem, Ann. of Math. (2) 141 (1995), 443–551.CrossRefGoogle Scholar