Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T07:39:57.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Hochschild homology of Hopf algebras and free Yetter–Drinfeld resolutions of the counit

Part of: Homological methods Selfadjoint operator algebras Hopf algebras, quantum groups and related topics

Published online by Cambridge University Press:  17 December 2012

Julien Bichon
Julien Bichon*
Affiliation:
Laboratoire de Mathématiques, Université Blaise Pascal, Complexe universitaire des Cézeaux, 63171 Aubière cedex, France (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

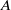We show that if $A$ and 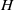$H$ are Hopf algebras that have equivalent tensor categories of comodules, then one can transport what we call a free Yetter–Drinfeld resolution of the counit of 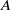$A$ to the same kind of resolution for the counit of $H$, exhibiting in this way strong links between the Hochschild homologies of 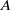$A$ and 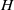$H$. This enables us to obtain a finite free resolution of the counit of 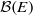$\mathcal {B}(E)$, the Hopf algebra of the bilinear form associated with an invertible matrix 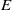$E$, generalizing an earlier construction of Collins, Härtel and Thom in the orthogonal case 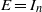$E=I_n$. It follows that 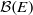$\mathcal {B}(E)$ is smooth of dimension 3 and satisfies Poincaré duality. Combining this with results of Vergnioux, it also follows that when 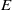$E$ is an antisymmetric matrix, the 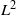$L^2$-Betti numbers of the associated discrete quantum group all vanish. We also use our resolution to compute the bialgebra cohomology of 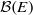$\mathcal {B}(E)$in the cosemisimple case.

Keywords

Hopf algebraHochschild homologyYetter–Drinfeld module$\uppercase {l}^2$-Betti numbers

MSC classification

Secondary: 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.) 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory 16T05: Hopf algebras and their applications
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 4 , April 2013 , pp. 658 - 678
Copyright
Copyright © 2012 The Author(s)

References

[Ban96]Banica, T., Théorie des représentations du groupe quantique compact libre $O(n)$, C. R. Acad. Sci. Paris Sér. I Math. 322 (1996), 241–244.Google Scholar
[BC07]Banica, T. and Collins, B., Integration over compact quantum groups, Publ. Res. Inst. Math. Sci. 43 (2007), 277–302.Google Scholar
[BCZ09]Banica, T., Collins, B. and Zinn-Justin, P., Spectral analysis of the free orthogonal matrix, Int. Math. Res. Not. IMRN (2009), 3286–3309.Google Scholar
[Bic10]Bichon, J., Hopf–Galois objects and cogroupoids, Pub. Mat. Uruguay, to appear, arXiv:1006.3014.Google Scholar
[Bic03a]Bichon, J., The representation category of the quantum group of a non-degenerate bilinear form, Comm. Algebra 31 (2003), 4831–4851.CrossRefGoogle Scholar
[Bic03b]Bichon, J., Hopf–Galois systems, J. Algebra 264 (2003), 565–581.Google Scholar
[BDV06]Bichon, J., De Rijdt, A. and Vaes, S., Ergodic coactions with large multiplicity and monoidal equivalence of quantum groups, Comm. Math. Phys. 262 (2006), 703–728.Google Scholar
[BG02]Brown, K. A. and Goodearl, K. R, Lectures on algebraic quantum groups, Advanced Courses in Mathematics CRM Barcelona (Birkhäuser, Basel, 2002).Google Scholar
[BZ08]Brown, K. A. and Zhang, J. J., Dualising complexes and twisted Hochschild (co)homology for Noetherian Hopf algebras, J. Algebra 320 (2008), 1814–1850.Google Scholar
[CMZ97]Caenepeel, S., Militaru, G. and Zhu, S., Crossed modules and Doi–Hopf modules, Israel J. Math. 100 (1997), 221–247.Google Scholar
[CMZ02]Caenepeel, S., Militaru, G. and Zhu, S., Frobenius and separable functors for generalized module categories and nonlinear equations, Lecture Notes in Mathematics, vol. 1787 (Springer, Berlin, 2002).Google Scholar
[CE56]Cartan, H. and Eilenberg, S., Homological algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
[CHT09]Collins, B., Härtel, J. and Thom, A., Homology of free quantum groups, C. R. Math. Acad. Sci. Paris 347 (2009), 271–276.Google Scholar
[CS05]Connes, A. and Shlyakhtenko, D., $L^2$-homology for von Neumann algebras, J. Reine Angew. Math. 586 (2005), 125–168.Google Scholar
[DL90]Dubois-Violette, M. and Launer, G., The quantum group of a non-degenerate bilinear form, Phys. Lett. B 245 (1990), 175–177.CrossRefGoogle Scholar
[FT91]Feng, P. and Tsygan, B., Hochschild and cyclic homology of quantum groups, Comm. Math. Phys. 140 (1991), 481–521.CrossRefGoogle Scholar
[GS90]Gerstenhaber, M. and Schack, S., Bialgebra cohomology, deformations and quantum groups, Proc. Natl Acad. Sci. USA 87 (1990), 78–81.Google Scholar
[GS92]Gerstenhaber, M. and Schack, S., Algebras, bialgebras, quantum groups, and algebraic deformations, Contemp. Math. 134 (1992), 51–92.Google Scholar
[GK93]Ginzburg, V. and Kumar, S., Cohomology of quantum groups at roots of unity, Duke Math. J. 69 (1993), 179–198.Google Scholar
[Gru04]Grunspan, C., Hopf-Galois systems and Kashiwara algebras, Comm. Algebra 32 (2004), 3373–3389.Google Scholar
[HK05]Hadfield, T. and Krähmer, U., Twisted homology of quantum $\mathrm {SL}(2)$, K-Theory 34 (2005), 327–360.Google Scholar
[Kas95]Kassel, C., Quantum groups, Graduate Texts in Mathematics, vol. 155 (Springer, Berlin, 1995).CrossRefGoogle Scholar
[KS97]Klimyk, A. and Schmüdgen, K., Quantum groups and their representations, Texts and Monographs in Physics (Springer, Berlin, 1997).Google Scholar
[KK10]Kowalzig, N. and Krähmer, U., Duality and products in algebraic (co)homology theories, J. Algebra 323 (2010), 2063–2081.CrossRefGoogle Scholar
[Kye08]Kyed, D., $L^2$-homology for compact quantum groups, Math. Scand. 103 (2008), 111–129.Google Scholar
[Kye 11]Kyed, D., On the zeroth $L^2$-homology of a quantum group, Münster J. Math. 4 (2011), 119–128.Google Scholar
[Lin77]Lin, B. I., Semiperfect coalgebras, J. Algebra 49 (1977), 357–373.Google Scholar
[Luc98]Lück, W., Dimension theory of arbitrary modules over finite von Neumann algebras and $L^2$-Betti numbers. I. Foundations, J. Reine Angew. Math. 495 (1998), 135–162.Google Scholar
[Luc02]Lück, W., L 2-invariants: theory and applications to geometry and K-theory (Springer, Berlin, 2002).CrossRefGoogle Scholar
[Mon93]Montgomery, S., Hopf algebras and their actions on rings (American Mathematical Society, Providence, RI, 1993).Google Scholar
[PW90]Parshall, B. and Wang, J., On bialgebra cohomology, Bull. Soc. Math. Belg. Sér. A 42 (1990), 607–642.Google Scholar
[Sch94]Schauenburg, P., Hopf modules and Yetter–Drinfeld modules, J. Algebra 169 (1994), 874–890.Google Scholar
[Sch96]Schauenburg, P., Hopf bigalois extensions, Comm. Algebra 24 (1996), 3797–3825.Google Scholar
[Sch04]Schauenburg, P., Hopf-Galois and bi-Galois extensions, Fields Inst. Commun. 43 (2004), 469–515.Google Scholar
[Tai04a]Taillefer, R., Injective Hopf bimodules, cohomologies of infinite-dimensional Hopf algebras and graded-commutativity of the Yoneda product, J. Algebra 276 (2004), 259–279.Google Scholar
[Tai04b]Taillefer, R., Cohomology theories of Hopf bimodules and cup-product, Algebr. Represent. Theory 7 (2004), 471–490.Google Scholar
[Tai07]Taillefer, R., Bialgebra cohomology of the duals of a class of generalized Taft algebras, Comm. Algebra (2007), 1415–1420.Google Scholar
[Tho08]Thom, A., $L^2$-cohomology for von Neumann algebras, Geom. Funct. Anal. 18 (2008), 251–270.Google Scholar
[VV08]Vaes, S. and Vander Vennet, N., Identification of the Poisson and Martin boundaries of orthogonal discrete quantum groups, J. Inst. Math. Jussieu 7 (2008), 391–412.Google Scholar
[VV07]Vaes, S. and Vergnioux, R., The boundary of universal discrete quantum groups, exactness, and factoriality, Duke Math. J. 140 (2007), 35–84.Google Scholar
[VdB98]Van den Bergh, M., A relation between Hochschild homology and cohomology for Gorenstein rings, Proc. Amer. Math. Soc. 126 (1998), 1345–1348; Erratum: Proc. Amer. Math. Soc. 130 (2002), 2809–2810.Google Scholar
[Ver07]Vergnioux, R., The property of rapid decay for discrete quantum groups, J. Operator Theory 57 (2007), 303–324.Google Scholar
[Ver12]Vergnioux, R., Paths in quantum Cayley trees and $L^2$-cohomology, Adv. Math. 229 (2012), 2686–2711.Google Scholar
[Voi11]Voigt, C., The Baum–Connes conjecture for free orthogonal quantum groups, Adv. Math. 227 (2011), 1873–1913.Google Scholar
[Wan95]Wang, S., Free products of compact quantum groups, Comm. Math. Phys. 167 (1995), 671–692.CrossRefGoogle Scholar
[Wei94]Weibel, C., An Introduction to Homological Algebra (Cambridge University Press, Cambridge, 1994).Google Scholar
[Wor98]Woronowicz, S. L., Compact quantum groups, in Symétries quantiques (Les Houches, 1995) (North-Holland, Amsterdam, 1998), 845–884.Google Scholar