Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-20T16:25:56.975Z Has data issue: false hasContentIssue false
  • English
  • Français

Hermitian forms over quaternion algebras

Part of: Cycles and subschemes Algebraic groups

Published online by Cambridge University Press:  15 September 2014

Nikita A. Karpenko  and
Alexander S. Merkurjev
Nikita A. Karpenko
Affiliation:
Mathematical and Statistical Sciences, University of Alberta, Edmonton, Canada email [email protected]
Alexander S. Merkurjev
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

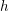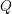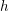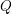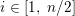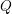We study a Hermitian form $h$ over a quaternion division algebra $Q$ over a field ($h$ is supposed to be alternating if the characteristic of the field is two). For generic $h$ and $Q$, for any integer $i\in [1,\;n/2]$, where $n:=\dim _{Q}h$, we show that the variety of $i$-dimensional (over $Q$) totally isotropic right subspaces of $h$ is 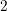$2$-incompressible. The proof is based on a computation of the Chow ring for the classifying space of a certain parabolic subgroup in a split simple adjoint affine algebraic group of type 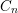$C_{n}$. As an application, we determine the smallest value of the 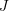$J$-invariant of a non-degenerate quadratic form divisible by a 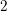$2$-fold Pfister form; we also determine the biggest values of the canonical dimensions of the orthogonal Grassmannians associated to such quadratic forms.

Keywords

algebraic groupsclassifying spacesHermitian and quadratic formsprojective homogeneous varietiesChow groups and motives

MSC classification

Primary: 14C25: Algebraic cycles 14L17: Affine algebraic groups, hyperalgebra constructions
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 12 , December 2014 , pp. 2073 - 2094
Copyright
© The Author(s) 2014 

References

Chernousov, V., Gille, S. and Merkurjev, A., Motivic decomposition of isotropic projective homogeneous varieties, Duke Math. J. 126 (2005), 137–159.Google Scholar
Edidin, D. and Graham, W., Equivariant intersection theory, Invent. Math. 131 (1998), 595–634.Google Scholar
Elman, R., Karpenko, N. and Merkurjev, A., The algebraic and geometric theory of quadratic forms, American Mathematical Society Colloquium Publications, vol. 56 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. / A Series of Modern Surveys in Mathematics, vol. 2, second edition (Springer, Berlin, 1998).CrossRefGoogle Scholar
Karpenko, N. A., Cohomology of relative cellular spaces and of isotropic flag varieties, Algebra i Analiz 12 (2000), 3–69.Google Scholar
Karpenko, N. A., Canonical dimension, in Proceedings of the international congress of mathematicians, vol. II (Hindustan Book Agency, New Delhi, 2010), 146–161.Google Scholar
Karpenko, N. A., Upper motives of outer algebraic groups, in Quadratic forms, linear algebraic groups, and cohomology, Developments in Mathematics, vol. 18 (Springer, New York, 2010), 249–258.Google Scholar
Karpenko, N. A., Hyperbolicity of unitary involutions, Sci. China Math. 55 (2012), 937–945.CrossRefGoogle Scholar
Karpenko, N. A., Sufficiently generic orthogonal Grassmannians, J. Algebra 372 (2012), 365–375.Google Scholar
Karpenko, N. A., Unitary Grassmannians, J. Pure Appl. Algebra 216 (2012), 2586–2600.CrossRefGoogle Scholar
Karpenko, N. A., Upper motives of algebraic groups and incompressibility of Severi–Brauer varieties, J. Reine Angew. Math. 677 (2013), 179–198.Google Scholar
Knus, M.-A., Merkurjev, A., Rost, M. and Tignol, J.-P., The book of involutions, American Mathematical Society Colloquium Publications, vol. 44 (American Mathematical Society, Providence, RI, 1998), with a preface in French by J. Tits.CrossRefGoogle Scholar
Manin, J. I., Correspondences, motifs and monoidal transformations, Mat. Sb. (N.S.) 77 (1968), 475–507.Google Scholar
Merkurjev, A. S., Panin, I. A. and Wadsworth, A. R., Index reduction formulas for twisted flag varieties. I, K-Theory 10 (1996), 517–596.Google Scholar
Milne, J. S., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Molina Rojas, L. A. and Vistoli, A., On the Chow rings of classifying spaces for classical groups, Rend. Semin. Mat. Univ. Padova 116 (2006), 271–298.Google Scholar
Rost, M., Chow groups with coefficients, Doc. Math. 1 (1996), 319–393 (electronic).Google Scholar
Scharlau, W., Quadratic and Hermitian forms, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 270 (Springer, Berlin, 1985).Google Scholar
Serre, J.-P., Cohomologie galoisienne, Lecture Notes in Mathematics, vol. 5, fifth edition (Springer, Berlin, 1994).Google Scholar
Springer, T. A., Linear algebraic groups, Modern Birkhäuser Classics, second edition (Birkhäuser, Boston, MA, 2009).Google Scholar
Totaro, B., The Chow ring of a classifying space, in Algebraic K-theory (Seattle, WA, 1997), Proceedings of Symposia in Pure Mathematics, vol. 67 (American Mathematical Society, Providence, RI, 1999), 249–281.Google Scholar
Vishik, A., On the Chow groups of quadratic Grassmannians, Doc. Math. 10 (2005), 111–130; (electronic).CrossRefGoogle Scholar
Vishik, A., Fields of u-invariant 2r + 1, in Algebra, arithmetic, and geometry: in honor of Yu. I. Manin, vol. II, Progress in Mathematics, vol. 270 (Birkhäuser, Boston, MA, 2009), 661–685.Google Scholar
Vistoli, A., Grothendieck topologies, fibered categories and descent theory, in Fundamental Algebraic Geometry, Mathematical Surveys and Monographs, vol. 123 (American Mathematical Society, Providence, RI, 2005), 1–104.Google Scholar