Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-20T16:20:44.289Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hardy–Littlewood conjecture and rational points

Part of: Diophantine equations Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  10 September 2014

Yonatan Harpaz ,
Alexei N. Skorobogatov  and
Olivier Wittenberg
Yonatan Harpaz
Affiliation:
Institute for Mathematics, Astrophysics and Particle Physics, Radboud University Nijmegen, Heyendaalseweg 135, 6525 AJ Nijmegen, The Netherlands email [email protected]
Alexei N. Skorobogatov
Affiliation:
Department of Mathematics, Imperial College London, SW7 2BZ, UK Institute for the Information Transmission Problems, Russian Academy of Sciences, 19 Bolshoi Karetnyi, Moscow 127994, Russia email [email protected]
Olivier Wittenberg
Affiliation:
Département de mathématiques et applications, École normale supérieure, 45 rue d’Ulm, 75230, Paris Cedex 05, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

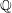Schinzel’s Hypothesis (H) was used by Colliot-Thélène and Sansuc, and later by Serre, Swinnerton-Dyer and others, to prove that the Brauer–Manin obstruction controls the Hasse principle and weak approximation on pencils of conics and similar varieties. We show that when the ground field is $\mathbb{Q}$ and the degenerate geometric fibres of the pencil are all defined over 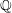$\mathbb{Q}$, one can use this method to obtain unconditional results by replacing Hypothesis (H) with the finite complexity case of the generalised Hardy–Littlewood conjecture recently established by Green, Tao and Ziegler.

Keywords

rational pointsfibration methodBrauer–Manin obstructiongeneralised Hardy–Littlewood conjecture

MSC classification

Primary: 14G05: Rational points 11D57: Multiplicative and norm form equations
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 12 , December 2014 , pp. 2095 - 2111
Copyright
© The Author(s) 2014 

References

Browning, T. D., Matthiesen, L. and Skorobogatov, A. N., Rational points on pencils of conics and quadrics with many degenerate fibres, Ann. of Math. (2) 180 (2014), 381–402.Google Scholar
Colliot-Thélène, J.-L., Groupe de Brauer non ramifié d’espaces homogènes de tores, J. Théor. Nombres Bordeaux 26 (2014), 69–83.Google Scholar
Colliot-Thélène, J.-L., Harari, D. and Skorobogatov, A. N., Valeurs d’un polynôme à une variable représentées par une norme, in Number theory and algebraic geometry, London Mathematical Society Lecture Note Series, vol. 303 (Cambridge University Press, London, 2003), 69–89.Google Scholar
Colliot-Thélène, J.-L., Harari, D. and Skorobogatov, A. N., Compactification équivariante d’un tore (d’après Brylinski et Künnemann), Expo. Math. 23 (2005), 161–170.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Sur le principe de Hasse et l’approximation faible, et sur une hypothèse de Schinzel, Acta Arith. 41 (1982), 33–53.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Principal homogeneous spaces under flasque tori: applications, J. Algebra 106 (1987), 148–205.CrossRefGoogle Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., La descente sur les variétés rationnelles. II, Duke Math. J. 54 (1987), 375–492.Google Scholar
Colliot-Thélène, J.-L. and Skorobogatov, A. N., Descent on fibrations over ¶k1 revisited, Math. Proc. Cambridge Philos. Soc. 128 (2000), 383–393.Google Scholar
Colliot-Thélène, J.-L., Skorobogatov, A. N. and Swinnerton-Dyer, P., Rational points and zero-cycles on fibred varieties: Schinzel’s hypothesis and Salberger’s device, J. Reine Angew. Math. 495 (1998), 1–28.Google Scholar
Colliot-Thélène, J.-L. and Swinnerton-Dyer, P., Hasse principle and weak approximation for pencils of Severi–Brauer and similar varieties, J. Reine Angew. Math. 453 (1994), 49–112.Google Scholar
Demarche, C. and Wei, D., Hasse principle and weak approximation for multinorm equations, Israel J. Math. (2014), doi:10.1007/s11856-014-1071-6. First published online June 20, 2014.Google Scholar
Frossard, E., Fibres dégénérées des schémas de Severi–Brauer d’ordres, J. Algebra 198 (1997), 362–387.CrossRefGoogle Scholar
Green, B. and Tao, T., Linear equations in primes, Ann. of Math. (2) 171 (2010), 1753–1850.Google Scholar
Green, B. and Tao, T., The Möbius function is strongly orthogonal to nilsequences, Ann. of Math. (2) 175 (2012), 541–566.Google Scholar
Green, B., Tao, T. and Ziegler, T., An inverse theorem for the Gowers U s+1[N]-norm, Ann. of Math. (2) 176 (2012), 1231–1372.CrossRefGoogle Scholar
Harari, D., Méthode des fibrations et obstruction de Manin, Duke Math. J. 75 (1994), 221–260.Google Scholar
Harari, D., Flèches de spécialisation en cohomologie étale et applications arithmétiques, Bull. Soc. Math. France 125 (1997), 143–166.Google Scholar
Hasse, H., Mathematische Abhandlungen, Vol. 1 (de Gruyter, Berlin, 1975).Google Scholar
Heath-Brown, R. and Skorobogatov, A. N., Rational solutions of certain equations involving norms, Acta Math. 189 (2002), 161–177.Google Scholar
Matthiesen, L., Linear correlations amongst numbers represented by positive definite binary quadratic forms, Acta Arith. 154 (2012), 235–306.Google Scholar
Matthiesen, L., Correlations of representation functions of binary quadratic forms, Acta Arith. 158 (2013), 245–252.Google Scholar
Salberger, P., Sur l’arithmétique de certaines surfaces de Del Pezzo, C. R. Acad. Sci. Paris Sér. I 303 (1986), 273–276.Google Scholar
Sansuc, J.-J., Groupe de Brauer et arithmétique des groupes algébriques linéaires sur un corps de nombres, J. Reine Angew. Math. 327 (1981), 12–80.Google Scholar
Schindler, D. and Skorobogatov, A. N., Norms as products of linear polynomials, J. Lond. Math. Soc. (2) 89 (2014), 559–580.Google Scholar
Schinzel, A. and Sierpinski, W., Sur certaines hypothèses concernant les nombres premiers, Acta Arith. 4 (1958), 185–208; Errata, Acta Arith. 5 (1959), 259.CrossRefGoogle Scholar
Serre, J.-P., Cohomologie galoisienne, Lecture Notes in Mathematics, vol. 5, fifth edition (Springer, Berlin, 1997).Google Scholar
Skorobogatov, A. N., Arithmetic on certain quadric bundles of relative dimension 2. I, J. Reine Angew. Math. 407 (1990), 57–74.Google Scholar
Skorobogatov, A. N., Descent on fibrations over the projective line, Amer. J. Math. 118 (1996), 905–923.Google Scholar
Skorobogatov, A., Torsors and rational points (Cambridge University Press, Cambridge, 2001).CrossRefGoogle Scholar
Swarbrick Jones, M., A note on a theorem of Heath-Brown and Skorobogatov, Q. J. Math. 64 (2013), 1239–1251.Google Scholar
Swinnerton-Dyer, P., Rational points on pencils of conics and on pencils of quadrics, J. Lond. Math. Soc. (2) 50 (1994), 231–242.Google Scholar
Swinnerton-Dyer, P., Topics in Diophantine equations, in Arithmetic geometry, Lecture Notes in Mathematics, vol. 2009 (Springer, Berlin, 2011), 45–110.Google Scholar
Wei, D., On the equation N K∕k(Ξ) = P (t), Proc. Lond. Math. Soc. (2014), doi:10.1112/plms/pdu035. First published online July 16, 2014.Google Scholar
Wittenberg, O., Intersections de deux quadriques et pinceaux de courbes de genre 1, Lecture Notes in Mathematics, vol. 1901 (Springer, 2007).Google Scholar