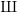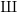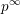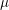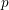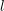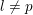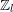Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pries, Rachel
and
Ulmer, Douglas
2016.
Arithmetic of abelian varieties in Artin-Schreier extensions.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 12,
p.
8553.
BETTS, L. ALEXANDER
DOKCHITSER, VLADIMIR
DOKCHITSER, V.
and
MORGAN, A.
2019.
Variation of Tamagawa numbers of semistable abelian varieties in field extensions.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 166,
Issue. 3,
p.
487.
Lim, Meng Fai
2021.
Some remarks on Kida’s formula when $$\mu \ne 0$$.
The Ramanujan Journal,
Vol. 55,
Issue. 3,
p.
1127.