Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-09T01:34:21.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry of shrinking Ricci solitons

Part of: Global differential geometry

Published online by Cambridge University Press:  29 July 2015

Ovidiu Munteanu  and
Jiaping Wang
Ovidiu Munteanu
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06268, USA email [email protected]
Jiaping Wang
Affiliation:
School of Mathematics, University of Minnesota, Minneapolis, MN 55455, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

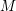The main purpose of this paper is to investigate the curvature behavior of four-dimensional shrinking gradient Ricci solitons. For such a soliton $M$ with bounded scalar curvature 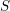$S$, it is shown that the curvature operator 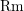$\text{Rm}$ of 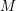$M$ satisfies the estimate 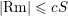$|\text{Rm}|\leqslant cS$ for some constant $c$. Moreover, the curvature operator 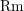$\text{Rm}$ is asymptotically nonnegative at infinity and admits a lower bound 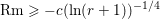$\text{Rm}\geqslant -c(\ln (r+1))^{-1/4}$, where $r$ is the distance function to a fixed point in 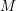$M$. As an application, we prove that if the scalar curvature converges to zero at infinity, then the soliton must be asymptotically conical. As a separate issue, a diameter upper bound for compact shrinking gradient Ricci solitons of arbitrary dimension is derived in terms of the injectivity radius.

Keywords

Ricci solitonscurvature estimatesdiameter

MSC classification

Primary: 53C44: Geometric evolution equations (mean curvature flow, Ricci flow, etc.) 53C21: Methods of Riemannian geometry, including PDE methods; curvature restrictions
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 12 , December 2015 , pp. 2273 - 2300
Copyright
© The Authors 2015 

References

Brendle, S., Rotational symmetry of self-similar solutions to the Ricci flow, Invent. Math. 194 (2013), 731–764.CrossRefGoogle Scholar
Cao, H. D., Recent progress on Ricci solitons, Adv. Lect. Math. (ALM) 11 (2010), 1–38.Google Scholar
Cao, H. D., Chen, B. L. and Zhu, X. P., Recent developments on Hamilton’s Ricci flow, in Geometric flows, Surveys in Differential Geometry, vol. 12 (International Press, Somerville, MA, 2008), 47–112.Google Scholar
Cao, H. D. and Chen, Q., On Bach-flat gradient shrinking Ricci solitons, Duke Math. J. 162 (2013), 1149–1169.CrossRefGoogle Scholar
Cao, H. D. and Zhou, D., On complete gradient shrinking Ricci solitons, J. Differential Geom. 85 (2010), 175–186.CrossRefGoogle Scholar
Chen, B. L., Strong uniqueness of the Ricci flow, J. Differential Geom. 82 (2009), 362–382.CrossRefGoogle Scholar
Chow, B. and Knopf, D., The Ricci flow: an introduction, Mathematical Surveys and Monographs, vol. 110 (American Mathematical Society, Providence, RI, 2004).CrossRefGoogle Scholar
Chow, B., Lu, P. and Ni, L., Hamilton’s Ricci flow, Graduate Studies in Mathematics, vol. 77 (American Mathematical Society, Providence, RI; Science Press, New York, 2006).CrossRefGoogle Scholar
Chow, B., Lu, P. and Yang, B., A lower bound for the scalar curvature of noncompact nonflat Ricci shrinkers, C. R. Math. Acad. Sci. Paris 349 (2011), 1265–1267.CrossRefGoogle Scholar
Eminenti, M., La Nave, G. and Mantegazza, C., Ricci solitons: the equation point of view, Manuscripta Math. 127 (2008), 345–367.CrossRefGoogle Scholar
Enders, J., Müller, R. and Topping, P., On Type-I singularities in Ricci flow, Comm. Anal. Geom. 19 (2011), 905–922.CrossRefGoogle Scholar
Fang, F., Man, J. and Zhang, Z., Complete gradient shrinking Ricci solitons have finite topological type, C. R. Math. Acad. Sci. Paris 346 (2008), 653–656.CrossRefGoogle Scholar
Feldman, M., Ilmanen, T. and Knopf, D., Rotationally symmetric shrinking and expanding gradient Ricci solitons, J. Differential Geom. 65 (2003), 169–209.CrossRefGoogle Scholar
Futaki, A., Li, H. and Li, X., On the first eigenvalue of the Witten–Laplacian and the diameter of compact shrinking solitons, Ann. Global Anal. Geom. 44 (2013), 105–114.CrossRefGoogle Scholar
Futaki, A. and Sano, Y., Lower diameter bounds for compact shrinking Ricci solitons, Asian J. Math. 17 (2013), 17–31.CrossRefGoogle Scholar
Hamilton, R., Three manifolds with positive Ricci curvature, J. Differential Geom. 17 (1982), 255–306.CrossRefGoogle Scholar
Hamilton, R., The formation of singularities in the Ricci flow, Surveys in Differential Geometry, vol. 2 (International Press, Somerville, MA, 1995), 7–136.Google Scholar
Haslhofer, R. and Müller, R., A compactness theorem for complete Ricci shrinkers, Geom. Funct. Anal. 21 (2011), 1091–1116.CrossRefGoogle Scholar
Haslhofer, R. and Müller, R., A note on the compactness theorem for 4-d Ricci shrinkers, Proc. Amer. Math. Soc., to appear, arXiv:1407.1683.Google Scholar
Kotschwar, B. and Wang, L., Rigidity of asymptotically conical shrinking gradient Ricci solitons, J. Differential Geom. 100 (2015), 55–108.CrossRefGoogle Scholar
Munteanu, O. and Wang, J., Smooth metric measure spaces with non-negative curvature, Comm. Anal. Geom. 19 (2011), 451–486.CrossRefGoogle Scholar
Munteanu, O. and Wang, M. T., The curvature of gradient Ricci solitons, Math. Res. Lett. 18 (2011), 1051–1069.CrossRefGoogle Scholar
Naber, A., Noncompact shrinking 4-solitons with nonnegative curvature, J. Reine Angew. Math. 645 (2010), 125–153.Google Scholar
Ni, L. and Wallach, N., On a classification of gradient shrinking solitons, Math. Res. Lett. 15 (2008), 941–955.CrossRefGoogle Scholar
Perelman, G., The entropy formula for the Ricci flow and its geometric applications, Preprint (2002), arXiv:math.DG/0211159.Google Scholar
Petersen, P. and Wylie, W., On the classification of gradient Ricci solitons, Geom. Topol. 14 (2010), 2277–2300.CrossRefGoogle Scholar
Shi, W. X., Deforming the metric on complete Riemannian manifolds, J. Differential Geom. 30 (1989), 223–301.Google Scholar