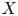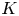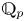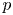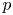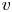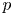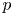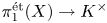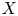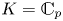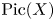A geometric p-adic Simpson correspondence in rank one

Abstract

For any smooth proper rigid space $X$ over a complete algebraically closed extension $K$ of $\mathbb {Q}_p$ we give a geometrisation of the $p$-adic Simpson correspondence of rank one in terms of analytic moduli spaces: the $p$-adic character variety is canonically an étale twist of the moduli space of topologically torsion Higgs line bundles over the Hitchin base. This also eliminates the choice of an exponential. The key idea is to relate both sides to moduli spaces of $v$-line bundles. As an application, we study a major open question in $p$-adic non-abelian Hodge theory raised by Faltings, namely which Higgs bundles correspond to continuous representations under the $p$-adic Simpson correspondence. We answer this question in rank one by describing the essential image of the continuous characters $\pi ^{{\mathrm {\acute {e}t}}}_1(X)\to K^\times$ in terms of moduli spaces: for projective $X$ over $K=\mathbb {C}_p$, it is given by Higgs line bundles with vanishing Chern classes like in complex geometry. However, in general, the correct condition is the strictly stronger assumption that the underlying line bundle is a topologically torsion element in the topological group $\operatorname {Pic}(X)$.

1. Introduction

The Corlette–Simpson correspondence for a smooth projective variety $X$ over $\mathbb {C}$ is an equivalence of categories between finite-dimensional $\mathbb {C}$-linear representations of the topological fundamental group $\pi _1(X)$ of $X(\mathbb {C})$ on the one hand, and semi-stable Higgs bundles on $X$ with vanishing (rational) Chern classes on the other hand [Sim92, § 1]. For any $n\in \mathbb {N}$, there are natural complex analytic moduli spaces of the rank-$n$ objects on either side, and the correspondence induces a homeomorphism between them, see [Sim92, Proposition 1.5] and [Sim95, Theorem 7.18]. However, this map does not respect the complex analytic structures.

Our first result is a very close $p$-adic analogue of this equivalence in rank one.

Theorem 1.1

1. (i) Let $X$ be a connected smooth projective variety over $\mathbb {C}_p$ and fix a point $x\in X(\mathbb {C}_p)$. Then any choice of an exponential map for $\mathbb {C}_p$ and of a flat $B_{\mathrm {dR}}^+/\xi ^2$-lift of $X$ induce an equivalence of categories

   \[ \bigg\{\begin{array}{@{}c@{}l}\text{one-dimensional continuous}\\\text{$\mathbb{C}_p$-representations of $\pi_1^{{\mathrm{\acute{e}t}}}(X,x)$} \end{array}\bigg\} {\tilde{\to}} \bigg\{\begin{array}{@{}c@{}l}\text{Higgs bundles on $X$ of rank one}\\\text{with vanishing Chern classes}\end{array}\bigg\}. \]
   By passing to isomorphism classes, this induces an isomorphism of topological groups
   \[ \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1^{{\mathrm{\acute{e}t}}}(X,x),\mathbb{C}_p^\times)\cong \operatorname{Pic}^{\tau}(X)\times H^0(X,\Omega^1(-1)). \]

2. (ii) More generally, let $X$ be a connected smooth proper rigid space over any complete algebraically closed field $K|\mathbb {C}_p$ and assume that the rigid analytic Picard functor of $X$ is representable by a rigid space $\mathbf {Pic}_X$. Then the analogous statements as in part (i) hold when we replace the condition of ‘vanishing Chern classes’ by the strictly stronger condition that the underlying line bundle is ‘topologically torsion’ in $\mathbf {Pic}_X(K)$.

This is the first instance of a correspondence relating $p$-adic continuous representations to Higgs bundles with an explicit topological condition. It gives useful insights into what to expect in higher rank, e.g. that Chern classes do not define the correct condition in general.

In order to clarify the statement of Theorem 1.1, we now elaborate on the terminology.

• – An exponential map for $K$ is a continuous group homomorphism $K\to 1+\mathfrak m_K$ splitting the $p$-adic logarithm $\log :1+\mathfrak m_K\to K$. Here $\mathfrak m_K$ is the maximal ideal of the ring of integers $\mathcal {O}_K$ of $K$. An exponential exists since $K$ is algebraically closed.

• – We define $\operatorname {Pic}^{\tau }(X)$ as the group of isomorphism classes of line bundles $L$ on $X$ for which there is $n\in \mathbb {N}$ such that $L^n$ defines a class in $\mathbf {Pic}^0_X(K)$, where $\mathbf {Pic}^0_X$ is the connected component of the identity of the rigid analytic Picard functor of $X$.

• – The topological group structures in Theorem 1.1(i) come from regarding either side as $K$-points of natural rigid moduli spaces (see § 1.1), endowed with the canonical topology inherited from $K$. For example, $\operatorname {Pic}^{\tau }(X)$ inherits a topology from $\mathbf {Pic}_X$.

• – The ‘topologically torsion’ condition in Theorem 1.1(ii) means that with respect to this topology on $\operatorname {Pic}^{\tau }(X)$, the line bundle $L$ satisfies $L^{n!}\to 1$ for $n\to \infty$.

1.1 Geometrising the $p$-adic Simpson correspondence of rank one

The main aim of this article is to show that, surprisingly, Theorem 1.1 can be upgraded to a geometric statement about moduli spaces: we show that there is always a smooth rigid analytic moduli space $\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$ of topologically torsion line bundles. This is an open rigid subgroup of the Picard variety $\mathbf {Pic}_{X}$ if the latter exists, but, in fact, we do not need representability of the Picard functor for the construction. Using the Hitchin base $\mathcal {A}$ of rank one, this allows us to define the ‘Dolbeault moduli space’ of topologically torsion Higgs line bundles

\[ \mathbf{M}_{\mathrm{Dol}}:=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \mathcal{A},\quad \text{where } \mathcal{A}:=H^0(X,\Omega^1(-1))\otimes_K\mathbb{G}_a. \]

On the other side of the $p$-adic Simpson correspondence, we have the $p$-adic character variety

\[ \mathbf{M}_{\mathrm{B}}:=\underline{\mathrm{Hom}}(\pi_1^{\mathrm{\acute{e}t}}(X,x),\mathbb{G}_m) \]

defined as the internal Hom in $v$-sheaves over $K$, where the profinite group $\pi _1^{\mathrm {\acute {e}t}}(X,x)$ is considered as a profinite $v$-sheaf. As we explain in § 3.1, the functor $\mathbf {M}_{\mathrm {B}}$ is represented by a rigid group variety, playing the role of the ‘Betti moduli space’ in this context. We show the following.

Theorem 1.2 (Theorem 4.1)

Let $X$ be a connected smooth proper rigid space over $K$ and fix $x\in X(K)$. Then there is a natural short exact sequence of rigid analytic groups

(1)\begin{equation} 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\to \mathbf{M}_{\mathrm{B}}\xrightarrow{\mathrm{HTlog}} \mathcal{A}\to 0. \end{equation}

On tangent spaces, the associated sequence of Lie algebras recovers the Hodge–Tate sequence

(2)\begin{equation} 0\to H^1_{\mathrm{an}}(X,\mathcal{O})\to H^1_{{\mathrm{\acute{e}t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p} K\xrightarrow{\mathrm{HT}} H^0(X,\Omega^1(-1))\to 0. \end{equation}

Here exactness of (1) is to be understood with respect to the étale topology. While the map $\mathrm {HTlog}$ in (1) can be defined explicitly using the $p$-adic logarithm, the first map is more subtle: it generalises and geometrises a construction of Deninger and Werner [DW05b], as well as of Song [Son22] in the case of curves over $\overline {\mathbb {Q}}_p$ as we explain in § 4. It induces a generalised ‘Weil pairing’

\[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \underline{\pi_1^{{\mathrm{\acute{e}t}}}(X,x)}\to \mathbb{G}_m, \]

namely a bilinear morphism of $v$-sheaves (or adic groups) where $\underline {\pi _1^{{\mathrm {\acute {e}t}}}(X,x)}$ is the profinite $v$-sheaf associated to the profinite group $\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$. We refer to Theorem 4.1 for more details.

We use Theorem 1.2 to describe a geometric $p$-adic Simpson correspondence in rank one in terms of a comparison of moduli spaces: the projection $\mathbf {M}_{\mathrm {Dol}}\to \mathcal {A}$ may be interpreted as the Hitchin fibration. Theorem 1.2 now yields an analogous map $\mathrm {HTlog}$ on the Betti side as follows.

From this perspective, Theorem 1.2 says that both $\mathbf {M}_{\mathrm {B}}$ and $\mathbf {M}_{\mathrm {Dol}}$ are $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$-torsors over $\mathcal {A}$, but the latter is split, whereas we show that the former is never split outside of trivial cases. It follows that we can regard $\mathbf {M}_{\mathrm {B}}$ as an étale twist of $\mathbf {M}_{\mathrm {Dol}}$. In fact, our main result is that one can more canonically compare these two torsors in a geometric fashion as follows.

Theorem 1.3 (Theorem 5.4 and Corollary 4.6)

We have $\mathbf {M}_{\mathrm {B}}\not \cong \mathbf {M}_{\mathrm {Dol}}$ as rigid spaces except in the trivial case that $H^0(X,\Omega _X)=0$. Instead, any choice of a flat $B^+_{\mathrm {dR}}/\xi ^2$-lift $\mathbb {X}$ of $X$ induces a natural $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$-torsor $\mathbb {L}_{\mathbb {X}}$ over $\mathcal {A}$ and a canonical isomorphism of rigid spaces

\[ \mathbf{M}_{\mathrm{B}}\times_{\mathcal{A}}\mathbb{L}_{\mathbb{X}}{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}\times_{\mathcal{A}}\mathbb{L}_{\mathbb{X}}. \]

Here the local system $\mathbb {L}_{\mathbb {X}}$ can roughly be thought of as a moduli space of exponentials, in the sense that it parametrises preimages of a certain logarithm map, see Definition 5.3. We also give a completely canonical variant of Theorem 1.3 over a moduli space of all lifts. These results explain the choices necessary in Faltings’ $p$-adic Simpson correspondence in a geometric fashion: any choice of an exponential induces a splitting of $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ on $K$-points. We take this as a first sign that in the $p$-adic situation, a more geometric formulation of the $p$-adic Simpson correspondence is possible. We will pursue this further in [Heu22c].

Remark 1.4 A choice of $\mathbb {X}$ induces a choice of splitting of the Hodge–Tate sequence (2), see [Guo23, Proposition 7.2.5]. If we are given a model of $X$ over a local field $L|\mathbb {Q}_p$, this induces such a lift $\mathbb {X}$, and Theorem 1.3 then provides a completely canonical comparison.

Remark 1.5 It is very surprising to us that the $p$-adic Simpson correspondence in rank one allows for a more refined comparison of the rigid analytic structures as in Theorem 1.3: if $X$ is instead a smooth projective curve over $\mathbb {C}$, the analogue of (1) is the exact sequence

(3)\begin{equation} 0\to \operatorname{Pic}^0(X)\to \operatorname{Hom}(\pi_1(X),\mathbb{C}^\times)\to H^0(X,\Omega^1)\to 0, \end{equation}

where the first map is defined as $\operatorname {Pic}^0(X)=\operatorname {Hom}(\pi _1(X),S^1)\to \operatorname {Hom}(H_1(X,\mathbb {Z}),\mathbb {C}^\times )$ using the decomposition $\mathbb {C}^\times =S^1\times \mathbb {R}^\times _+$; see [Sim92, p. 21] and [Sim93, § 2]. This is clearly only real-analytic and not complex-analytic. Instead, the only result we know in the literature that resembles Theorem 1.3 is Groechenig's result in the mod-$p$-Simpson correspondence that for curves over $\overline {\mathbb {F}}_p$, the de Rham moduli stack is a twist of the Dolbeault moduli stack [Gro16].

We now discuss the precise relation to previous results in the $p$-adic Simpson correspondence, and explain in more detail the topologically torsion condition and the moduli spaces.

1.2 The conjectural $p$-adic Simpson correspondence: known results

Let $K|\mathbb {Q}_p$ be any complete algebraically closed extension and let $X$ be a connected smooth proper rigid space over $K$ with fixed base-point $x\in X(K)$. In this setting, the conjectural $p$-adic Simpson correspondence is expected to be an equivalence of categories (depending on choices)

(4)\begin{equation} \bigg\{\begin{array}{@{}c@{}l}\text{finite-dimensional continuous }\\ \text{$K$-linear representations of $\pi_1^{{\mathrm{\acute{e}t}}}(X,x)$} \end{array}\bigg\} {\tilde{\to}} \bigg\{\begin{array}{@{}c@{}l}\text{Higgs bundles on $X$}\\ \text{satisfying$\ldots$??}\end{array}\bigg\}, \end{equation}

where ‘??’ is a condition yet to be identified. In order to construct a fully faithful functor from representations to Higgs bundles, Faltings [Fal05] introduced a category of ‘generalised representations’ into which representations of $\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ embed fully faithfully. This category can be shown to be equivalent to the category of $v$-vector bundles on $X$ (see [Heu22a, Proposition 2.3]). If we gloss over some technical differences in setups, then reformulated in this language, Faltings proved that if $X$ is a smooth projective curve, there is an equivalence

(5)\begin{equation} \{\text{$v$-vector bundles on $X$}\} {\tilde{\to}} \{\text{Higgs bundles on $X$}\}. \end{equation}

More generally, such an equivalence has recently been constructed in [Heu23, Theorem 1.1] for any smooth proper rigid space $X$ over $K$. Previously, Faltings constructed a ‘local’ version of this correspondence under additional ‘smallness’ assumptions, which was reinterpreted in terms of period rings and studied in detail by Abbes, Gros and Tsuji [AGT16]. There are other known instances of this, e.g. due to Wang for $X$ of good reduction [Wan23]. In rank one, we previously constructed the equivalence (5) for general $X$ by way of a ‘Hodge–Tate sequence for $\mathbb {G}_m$’ for the group $\operatorname {Pic}_v(X)$ of isomorphism classes of $v$-line bundles on $X$: a short exact sequence

(6)\begin{equation} 0\to \operatorname{Pic}_{{\mathrm{\acute{e}t}}}(X)\to \operatorname{Pic}_v(X)\to H^0(X,\Omega^1(-1))\to 0, \end{equation}

see [Heu22b]. We note that neither of the (conjectural) equivalences (4) and (5) is canonical, instead they will depend on choices of an exponential for $K$ and a flat $B_{\mathrm {dR}}^+/\xi ^2$-lift of $X$. For example, these choices induce a splitting of (6), which is not canonically split.

Given correspondence (5), a fundamental open problem in $p$-adic non-abelian Hodge theory, raised by Faltings in [Fal05, § 5], is to find the condition ‘??’.

Question 1.6 Which Higgs bundles on $X$ correspond to continuous representations of $\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ under the $p$-adic non-abelian Hodge correspondence (5)?

In the case of vanishing Higgs field, this question had been studied by Deninger and Werner [DW05b, DW20] prior to Faltings’ article. Based on their work, Xu has recently made progress on Question 1.6 in the case of curves by identifying a condition for Higgs bundles to be ‘potentially Deninger–Werner’, from which he is able to construct a functor to representations [Xu22]. This raises the question if this condition has a more classical description that can be used in practice to see whether a Higgs bundle is ‘potentially Deninger–Werner.’

The construction of Deninger–Werner has been extended to the rigid analytic setup by Würthen [Wür23, § 3], whose results suggest that in the special case of vanishing Higgs field, pro-finite-étale vector bundles give the correct subcategory of Higgs bundles. Here a vector bundle is called pro-finite-étale if it becomes trivial on a pro-finite-étale cover in Scholze's pro-étale site [Sch13] (we note that this is strictly stronger than being trivialised by a finite étale cover). Such vector bundles were further studied in [MW23]. We showed in [Heu22b, § 5] that the pro-finite-étale condition also gives the correct category for all Higgs bundles in rank one, namely we constructed an equivalence as in (4) where the left-hand side consist of continuous characters and the right-hand side of Higgs line bundle whose underlying line bundle is pro-finite-étale. In [HMW23], we deduced that on abelian varieties, the answer to Question 1.6 is given by pro-finite-étale Higgs bundles also in higher rank.

However, these results in turn raise the question how pro-finite-étale vector bundles can be characterised more classically, as it is a priori difficult to verify that a given vector bundle is pro-finite-étale. In [Heu22b, § 5], we characterised pro-finite-étale line bundles as those admitting a reduction of structure group to a certain subsheaf $\mathbb {G}_m^{\mathrm {tt}}\subseteq \mathbb {G}_m$, but we left it open how such line bundles can be described more concretely, e.g. in terms of the Picard variety.

Theorem 1.1 now gives a fully satisfactory answer to this question, thus to Question 1.6, for line bundles on any smooth proper rigid space. One reason why we think this description is the ‘correct’ one is that it is geometric, i.e. it can be phrased in terms of moduli spaces, opening up a completely new possibility for a geometric formulation of the $p$-adic Simpson correspondence: we believe that Theorem 1.3 stands a chance of being generalised to higher rank, as we will explore further in [Heu22c]. Moreover, this suggests that a moduli-theoretic approach to non-abelian Hodge theory may help answer Question 1.6 in general.

1.3 A new geometric approach via diamantine Picard functors

We now elaborate on our strategy to prove Theorems 1.1–1.3, as well as on the construction of the moduli spaces, which yields additional results of independent interest.

A crucial new technical ingredient to this article are the diamantine Picard functors introduced for this purpose in [Heu21a]: to motivate this, let us first mention that we show that a line bundle $L$ on $X$ is pro-finite-étale if and only if it extends to a line bundle on the adic space $X\times \underline {\widehat {\mathbb {Z}}}$ whose specialisation at each $n\in \mathbb {Z}\subseteq \widehat {\mathbb {Z}}$ is isomorphic to $L^n$. Here $\underline {\widehat {\mathbb {Z}}}$ denotes the adic space over $\operatorname {Spa}(K)$ which represents the $v$-sheaf $\varprojlim _{N\in \mathbb {N}} \underline {\mathbb {Z}/N\mathbb {Z}}$ over $K$.

We would like to say that this induces a morphism of adic spaces from $\underline {\widehat {\mathbb {Z}}}$ to the rigid Picard variety of $X$. However, $\underline {\widehat {\mathbb {Z}}}$ is no longer a rigid space, rather it is perfectoid. We therefore use the diamantine Picard functor $\mathbf {Pic}_{X}$ defined on perfectoid test objects. More precisely, according to (6), there are two different such functors, one for étale line bundles, denoted by $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$, the other for $v$-line bundles, denoted by $\mathbf {Pic}_{X,v}$. Explicitly, for $\tau \in \{{\mathrm {\acute {e}t}},v\}$,

\[ \mathbf{Pic}_{X,\tau}:\operatorname{Perf}_K\to \mathrm{Ab}, \quad T\mapsto \operatorname{Pic}_\tau(X\times T)/\operatorname{Pic}_\tau(T). \]

In order to characterise maps to $\mathbf {Pic}_{X,\tau }$ that ‘extend ${\widehat {\mathbb {Z}}}$-linearly’ as previously, we now define the following.

Definition 1.7 For any $v$-sheaf $F$ on $\operatorname {Perf}_K$, the topologically torsion subsheaf $F^\mathrm {tt}\subseteq F$ is the sheaf-theoretic image of the map $\underline {\mathrm {Hom}}(\underline {\widehat {\mathbb {Z}}},F)\to F$ given by evaluation at $1\in {\widehat {\mathbb {Z}}}$.

We give a more classical description of $F^\mathrm {tt}$ when $F$ is a rigid group: for example, the aforementioned topologically torsion subsheaf $\mathbb {G}_m^\mathrm {tt}\subseteq \mathbb {G}_m$ can be shown to be represented by the open subgroup generated by the open unit disc around $1$ and the roots of unity.

These definitions, combined with a systematic study of topologically torsion subsheaves, allow us to give a much more conceptual characterisation of pro-finite-étale line bundles than that we gave previously in [Heu22b, Theorem 5.7.3]: namely, in the category of diamonds, there is a universal pro-finite-étale cover $\widetilde X\to X$, a pro-finite-étale torsor under $\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$. The following result now describes which line bundles are trivialised by pro-finite-étale covers, or equivalently by $\widetilde X$ and, thus, give rise to $p$-adic characters.

Theorem 1.8 (Theorem 3.6)

Let $\tau \in \{{\mathrm {\acute {e}t}},v\}$. There is a short exact sequence of sheaves

\[ 0\to \mathbf{Pic}^{\mathrm{tt}}_{X,\tau}\to \mathbf{Pic}_{X,\tau}\to \mathbf{Pic}_{\widetilde X,\tau} \]

on $\operatorname {Perf}_{K,\tau }$. The Cartan–Leray sequence of $\widetilde X\to X$ thus induces a canonical isomorphism

\[ \mathbf{Pic}^{\mathrm{tt}}_{X,v}=\underline{\mathrm{Hom}}(\pi_1^{{\mathrm{\acute{e}t}}}(X,x),\mathbb{G}_m). \]

Here we crucially use that $\mathbf {Pic}_{X,\tau }$ is defined on perfectoid test objects such as $\underline {\widehat {\mathbb {Z}}}$. On $K$-points, we deduce that the line bundles on $X$ trivialised by $\widetilde X$ are given by $\mathbf {Pic}^{\mathrm {tt}}_{X,{\mathrm {\acute {e}t}}}(K)=\operatorname {Pic}(X)^\mathrm {tt}$, i.e. those classes $L$ in the topological group $\operatorname {Pic}(X)$ for which $L^{n!}\to 1$ for $n\to \infty$. To deduce Theorem 1.1, we show that for projective $X$ over $\mathbb {C}_p$, we in fact have

(7)\begin{equation} \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}(\mathbb{C}_p)=\operatorname{Pic}_{{\mathrm{\acute{e}t}}}^{\tau}(X), \end{equation}

where $\operatorname {Pic}_{{\mathrm {\acute {e}t}}}^{\tau }(X)$ is the group of line bundles with torsion Néron–Severi class. These are precisely the line bundles with vanishing (rational) Chern classes. To see (7), we use that $\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ is represented by an abelian variety $A$ over $\mathbb {C}_p$, and we show that $A^\mathrm {tt}(\mathbb {C}_p)=A(\mathbb {C}_p)$. For this, we use that the residue field of $\mathbb {C}_p$ is a union of finite fields, and that $v_p(\mathbb {C}_p)=\mathbb {Q}$.

On the other hand, this shows that finding the correct condition ‘??’ in (4) is very subtle.

Remark 1.9 Over any extension $K\supsetneq \mathbb {C}_p$, the inclusion $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(K)\subseteq \operatorname {Pic}^{\tau }(X)$ can become strict: if $X$ is a curve of good reduction over $K$ with Jacobian $J=\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}$, then $J(K)^\mathrm {tt}$ are precisely those points of $J(K)$ that reduce to a torsion point on the special fibre. This special case of curves with good reduction is implicit in Faltings’ discussion in [Fal05, p. 856].

Remark 1.10 Already over $\mathbb {C}_p$, the equality (7) and, thus, the first part of Theorem 1.1 can become false if we only assume that $X$ is proper rather than projective, since $\mathbf {Pic}^0_X$ is then no longer necessarily an abelian variety: for example, if $X$ is a Hopf variety, then $\mathbf {Pic}_X=\mathbb {G}_m$ (see [HL00, Remark 0.1.3]). However, we have $\mathbb {G}_m^\mathrm {tt}(\mathbb {C}_p)=\mathcal {O}_{\mathbb {C}_p}^\times \subsetneq \mathbb {C}_p^\times =\mathbb {G}_m(\mathbb {C}_p)$.

Remark 1.11 In terms of rigid spaces in the sense of Tate, the map $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\hookrightarrow \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ may by (7) be an open bijective map that is no longer surjective when passing to adic spaces.

From this perspective, it arguably feels like a coincidence that ‘vanishing Chern classes’ are the correct answer to Question 1.6 for line bundles on projective varieties over $\mathbb {C}_p$. Instead, as already in rank one the cleanest formulation of the condition of ‘topologically torsion’ requires the geometric structure of $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ as a rigid space, this suggests that in general, analytic moduli spaces may be necessary to answer Question 1.6 over general fields.

Structure of the article

In § 2 we introduce the notion of topologically torsion subsheaves and study these systematically. In particular, with an eye towards applications to Picard varieties, we study topologically torsion subsheaves of rigid groups.

In § 3 we introduce the $p$-adic character variety and explain why this is isomorphic to the topologically torsion subsheaf of the $v$-Picard functor, that is we prove Theorem 1.8.

In § 4 we prove Theorem 1.2. We also give the application to Deninger and Werner's map by constructing a generalised Weil pairing. As a further application, we comment on applications to the study of the structure of rigid Picard functors.

In § 5, we prove the étale comparison of Betti and Dolbeault moduli spaces, Theorem 1.3, as well as several related comparison isomorphisms.

Notation

Throughout, let $K$ be a (complete) non-archimedean field of residue characteristic $p$. We denote by $\mathcal {O}_K=K^{\circ }$ the ring of integers consisting of power-bounded elements. More generally, we denote by $K^+\subseteq K$ any ring of integral elements. Let $\mathfrak {m}\subseteq K^+$ be the maximal ideal, and $\Gamma$ the value group. From § 3 on, $K$ will be a perfectoid field extension of $\mathbb {Q}_p$ in the sense of [Sch12], and we then use almost mathematics with respect to $\mathfrak {m}$.

By a rigid space over $(K,K^+)$ we mean an adic space locally of topologically finite type over $\operatorname {Spa}(K,K^+)$. In the following, we often abbreviate $\operatorname {Spa}(K,K^+)$ by $\operatorname {Spa}(K)$ when the ring $K^+$ is clear from the context. In particular, we then denote by $\mathrm {SmRig}_{K}$ the category of smooth rigid spaces over $\operatorname {Spa}(K,K^+)$, by $\operatorname {Perf}_{K}$ the category of perfectoid spaces over $(K,K^+)$, and by $\mathrm {LSD}_{K}$ the category of locally spatial diamonds over $\mathrm {Spd}(K,K^+)$ in the sense of [Sch18, § 11]. More generally, for any rigid space $X$ we denote by $\mathrm {SmRig}_{X}$ the slice category of rigid spaces over $X$. In accordance with this notation, for any two rigid spaces $X$ and $Y$ over $K$, we also write $Y_X:=Y\times _KX$. Similarly for the other categories.

We denote by $\mathbb {B}^d$ the rigid unit polydisc of dimension $d$ over $(K,K^+)$, by $\mathbb {G}_m$ the rigid torus over $(K,K^+)$ defined as the analytification of the algebraic torus, and similarly by $\mathbb {G}_a$ the rigid affine line with its additive structure. We denote by $\widehat {\mathbb {G}}_m$ the open unit disc around $1$ in $\mathbb {G}_m$. These are all examples of rigid groups: by a rigid group we mean a group object in the category of rigid spaces over $(K,K^+)$. In this article, we always assume this to be commutative without further mention. Similarly for adic groups.

There is a fully faithful diamondification functor $\mathrm {SmRig}_{K}\hookrightarrow \mathrm {LSD}_{K}$, $X\mapsto X^\diamondsuit$, see [Sch18, § 15.6], and we shall freely identify $X$ with its image under this functor. In particular, we often drop the diamond $-^\diamondsuit$ from notation. For example, we just write $X_v$ for the $v$-site $X^\diamondsuit _v$.

For any formal scheme $\mathfrak S$ over $\operatorname {Spf}(K^+)$, we denote by $\mathfrak S^\mathrm {ad}_{\eta }:=\mathfrak S^\mathrm {ad}\times _{\operatorname {Spa}(K^+,K^+)}\operatorname {Spa}(K,K^+)$ the adic generic fibre in the sense of Scholze and Weinstein [SW13, § 2.2]. If $\mathfrak S$ is locally of topologically finite type over $\operatorname {Spf}(K^+)$, this is a rigid space over $\operatorname {Spa}(K,K^+)$ in the above sense. We say that a rigid space has good reduction if it is isomorphic to $\mathfrak S^\mathrm {ad}_{\eta }$ for some formal scheme $\mathfrak S$ that is smooth over $\operatorname {Spf}(K^+)$.

2. The topologically torsion subsheaf

The purpose of this section is to introduce a new technical device that plays a key role in this article: the topologically torsion subgroup of a $v$-sheaf.

2.1 Locally profinite $v$-sheaves

We start by recalling the definition of locally constant sheaves, and record some basic lemmas for later reference. For this it is beneficial to work in greater generality than in the introduction, over general non-archimedean fields $(K,K^+)$. We first adapt [Sch18, Example 11.12] to this setting.

Definition 2.1 Let $X$ be an adic space over $\operatorname {Spa}(K,K^+)$. Then we have a natural injective map $X(K,K^+)\hookrightarrow |X|$ sending a morphism $x:\operatorname {Spa}(K,K^+)\to X$ to the image of the unique closed point under $x$. We use this to endow $X(K,K^+)$ with the subspace topology.

Definition 2.2 For any locally profinite set $G$ we define a locally profinite $v$-sheaf $\underline {G}$.

1. (i) If $G$ is a discrete topological space, then we associate to $G$ the locally constant sheaf $\underline {G}$ on $\operatorname {Perf}_{K,v}$ that is the sheafification of the presheaf $X\mapsto G$. This is represented by the adic space $\sqcup _G\operatorname {Spa}(K,K^+)$.

2. (ii) If $G=\varprojlim _{i\in I} G_i$ is a profinite set where the $G_i$ are finite sets considered as discrete topological spaces, then we associate to $G$ the $v$-sheaf of sets $\underline {G}:=\textstyle \varprojlim _{i\in I} \underline {G_i}$. By [SW13, Proposition 2.4.5], this is represented by the affinoid adic space

   \[ \underline{G}=\operatorname{Spa}(\operatorname{Map}_{{\operatorname{cts}}}(G,K),\operatorname{Map}_{{\operatorname{cts}}}(G,K^+))\sim \textstyle\varprojlim_{i\in I}\underline{G_i}. \]
   This is sheafy as by Lemma 2.3, any cover of $|\underline {G}|$ admits a disjoint refinement.

3. (iii) In both the profinite and the discrete case, we have a natural homeomorphism $|\underline {G}|=|\operatorname {Spa}(K,K^+)|\times G$ by Lemma 2.3. Simultaneously generalising both parts (i) and (ii), we can therefore extend the definition to locally profinite sets $G$ by glueing.

If $G$ is a locally profinite group, then $\underline {G}$ inherits the structure of an adic group: this is immediate from the observation that the functor $\underline {\phantom {-}}$ commutes with finite products.

The following lemma was used in the definition.

Lemma 2.3 Let $G$ be a locally profinite set, then we have natural homeomorphisms

\[ |\underline{G}|=|\operatorname{Spa}(K,K^+)|\times G \quad \text{and} \quad \underline{G}(K,K^+)=G. \]

Proof. We can reduce to profinite sets $G=\varprojlim G_i$, for which we have

\[ |\underline{G}|=\varprojlim |G_i| \quad \text{and} \quad \underline{G}(K,K^+)=\varprojlim G_i(K,K^+). \]

This reduces us to the case of finite sets, where the statements are clear.

Lemma 2.4 Let $H$ be a locally profinite set, and let $G$ be any adic space over $(K,K^+)$. Then

\[ \operatorname{Mor}_K(\underline{H},G)=\operatorname{Map}_{{\operatorname{cts}}}(H,G(K,K^+)), \]

functorially in $H$ and $G$. If $H$ is a locally profinite group and $G$ is an adic group for which $G(K,K^+)$ is a topological group, this induces

\[ \operatorname{Hom}(\underline{H},G)=\operatorname{Hom}_{{\operatorname{cts}}}(H,G(K,K^+)). \]

Proof. The second part of the lemma will follow from the first by functoriality.

For the first part, evaluation on $(K,K^+)$-points defines by Lemma 2.3 a morphism

\[ \operatorname{Map}(\underline{H},G)\to \operatorname{Map}_{{\operatorname{cts}}}(H,G(K,K^+)). \]

Here continuity is clear as $G(K,K^+)$ has the subspace topology of $|G|$, and $H$ that of $|\underline {H}|$.

The map is clearly functorial in $H$ and $G$. To see that it is a bijection, we can therefore by glueing reduce to the case that $H$ is profinite and $G$ is affinoid.

Given a continuous map $\varphi :H\to G(K,K^+)$, there is an associated map of $K^+$-algebras

\[ \mathcal{O}^+(G)\to \operatorname{Map}_{{\operatorname{cts}}}(H,K^+) \]

that interprets $f\in \mathcal {O}^+(G)$ as a map $f:G\to \mathbb {B}^1:=\operatorname {Spa}(K\langle X\rangle,K^+\langle X\rangle )$ and sends it to

\[ H\xrightarrow{\varphi} G(K,K^+)\xrightarrow{f} \mathbb{B}^1(K,K^+)=K^+. \]

This is clearly functorial in $H$ and $G$. We have thus defined natural morphisms

\[ \operatorname{Map}_{{\operatorname{cts}}}(H,G(K,K^+)) \to \operatorname{Map}(\underline{H},G)\to \operatorname{Map}_{{\operatorname{cts}}}(H,G(K,K^+)). \]

It is now formal from the functoriality that these compose to the identity: we can first reduce to the case $H=\{x\}$ and then to $G=\operatorname {Spa}(K,K^+)$, for which the statement is clear.

It remains to prove that the second map in the above composition is injective. For this, consider the topological space $H'$ whose underlying set is that of $H$, but endowed with the discrete topology. There is by functoriality a natural map $\underline {H'}\to \underline {H}$, which on global sections

\[ \mathcal{O}^+(\underline{H})=\operatorname{Map}_{{\operatorname{cts}}}(H,K^+)\to \mathcal{O}^+(\underline{H'})=\operatorname{Map}(H',K^+) \]

is injective. Consequently, so is the pullback $\operatorname {Map}(\underline {H},G)\to \operatorname {Map}(\underline {H},G)$ for affinoid $G$. We are therefore reduced to the case of discrete $H$, where the lemma is clear.

2.2 Topologically torsion sheaves

From now on, let $K$ be a perfectoid field, and $K^+\subseteq K$ a ring of integral elements as before. We work in the category of $v$-sheaves on $\operatorname {Perf}_K$. For a locally profinite set $G$, to simplify notation, from now on we also denote just by $G$ the pro-constant $v$-sheaf $\underline {G}$ from Definition 2.2 when it is clear from the context what is meant.

Definition 2.5 Let $F$ be an abelian $v$-sheaf on $\operatorname {Perf}_K$.

1. (i) Consider the internal Hom sheaf $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},F)$ where

   \[ {\widehat{\mathbb{Z}}}:=\underline{{\widehat{\mathbb{Z}}}}=\varprojlim_{N\in\mathbb{N}} \underline{\mathbb{Z}/N\mathbb{Z}} \]
   is the profinite sheaf of Definition 2.2. There is a natural evaluation map at $1\in {\widehat {\mathbb {Z}}}$:
   \[ \mathrm{e}_F:\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},F)\to F. \]
   We define the topologically torsion subsheaf of $F$ to be the abelian subsheaf
   \[ F^\mathrm{tt}=\mathrm{im}(\mathrm{e}_F)\subseteq F. \]

2. (ii) We say that a $v$-sheaf $F$ is topologically torsion if $F^\mathrm {tt}\to F$ is an isomorphism.

3. (iii) We say that $F$ is strongly topologically torsion if already $\mathrm e_F$ is an isomorphism.

4. (iv) We say that $F$ is topologically torsionfree if $F^\mathrm {tt}=0$.

Definition 2.6 We make analogous definitions for the topologically $p$-torsion subsheaf

\[ F\langle p^\infty\rangle:=\mathrm{im}\big(\underline{\mathrm{Hom}}(\mathbb{Z}_p,F)\to F\big)\subseteq F \]

by replacing ${\widehat {\mathbb {Z}}}$ with $\mathbb {Z}_p$. Via the natural projection ${\widehat {\mathbb {Z}}}\twoheadrightarrow \mathbb {Z}_p$, we see that $F\langle p^\infty \rangle \subseteq F^{\mathrm {tt}}\subseteq F$. In particular, if $F$ is topologically $p$-torsion, it is automatically topologically torsion.

Example 2.7 As we show in § 2.3, for the $v$-sheaf represented by the rigid group $\mathbb {G}_m$, the sheaf $\mathbb {G}_m\langle p^\infty \rangle \subseteq \mathbb {G}_m$ is given by the open unit disc $\widehat {\mathbb {G}}_m\subseteq \mathbb {G}_m$ of radius 1 around 1, and $\mathbb {G}_m^\mathrm {tt}$ is the open subgroup given by the translates by all roots of unity $\mu _N\subseteq \mathbb {G}_m$ for $N\in \mathbb {N}$.

Remark 2.8 The construction of $F\langle p^\infty \rangle$ may be seen as an analogue for $v$-sheaves of a related construction by Fargues [Far19, §§ 1.6 and 2.4] for rigid groups in characteristic zero which gives rise to analytic $p$-divisible groups in the sense of Fargues, cf. § 2.3. This is what motivates our notation.

Lemma 2.9 For any abelian $v$-sheaf $F$, the sheaf $F^\mathrm {tt}$ is itself topologically torsion. Sending $F\mapsto F^\mathrm {tt}$ thus defines a right-adjoint to the forgetful functor from topologically torsion abelian $v$-sheaves to abelian $v$-sheaves. The analogous statements hold for $F\langle p^\infty \rangle$.

Proof. It suffices to show that the natural map $(F^{\mathrm {tt}})^\mathrm {tt}\to F^{\mathrm {tt}}$ is an isomorphism. It is then formal that this defines the unit of an adjunction with co-unit given by $F^\mathrm {tt}\to F$.

It suffices to show that the map is surjective, for which it suffices to prove that the map $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},F^{\mathrm {tt}})\to F^{\mathrm {tt}}$ is surjective. For this it suffices to prove that the top map in the diagram

is surjective. This holds because for any perfectoid space $T$ over $K$ and any $T$-linear homomorphism $\varphi :{\widehat {\mathbb {Z}}}\times T\to F$, a preimage is given by the map ${\widehat {\mathbb {Z}}}\times {\widehat {\mathbb {Z}}}\times T\to F$ defined by $(a,b,x)\mapsto \varphi (ab,x)$. Thus, $F^\mathrm {tt}$ is topologically torsion. The case of $F\langle p^\infty \rangle$ is analogous.

Example 2.10 The reason why we need both the notion of topologically torsion and strongly topologically torsion sheaves is that each has its advantages and pathologies.

1. (i) For an example where $F\langle p^\infty \rangle \neq \underline {\mathrm {Hom}}(\mathbb {Z}_p,F)$, consider the $v$-sheaf $F=\mathbb {Z}_p/\mathbb {Z}$ in the exact sequence

   \[ 0\to \mathbb{Z}\to \mathbb{Z}_p\to\mathbb{Z}_p/\mathbb{Z}\to 0. \]
   One can show that $\underline {\mathrm {Hom}}(\mathbb {Z}_p,F)=\underline {\mathbb {Q}_p}$ (see [Heu21c, § 2.3]), but nevertheless $F\langle p^\infty \rangle =F$. This also shows that the category of topologically torsion sheaves is not abelian, that subsheaves of topologically torsion sheaves need not be topologically torsion, and that in contrast to $\underline {\mathrm {Hom}}(\mathbb {Z}_p,-)$, the functor $-\langle p^\infty \rangle$ is neither left-exact nor right-exact.

2. (ii) On the other hand, the analogue of Lemma 2.9 does not hold for $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$, namely

   \[ \underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},-))\to \operatorname{Hom}({\widehat{\mathbb{Z}}},-) \]
   is not an equivalence: indeed, by the Yoneda Lemma and the tensor-hom adjunction this follows from the fact that ${\widehat {\mathbb {Z}}}\to {\widehat {\mathbb {Z}}}\otimes _{\mathbb {Z}}{\widehat {\mathbb {Z}}}$ is not an isomorphism of $v$-sheaves.

We show in § 2.3 that such pathologies cannot occur for $v$-sheaves represented by rigid spaces. However, we first prove some useful lemmas that hold in greater generality.

Lemma 2.11

1. (i) The cokernel of $F^\mathrm {tt}\to F$ is torsionfree.

2. (ii) The cokernel of $F\langle p^\infty \rangle \to F$ is $p$-torsionfree.

Proof. The $v$-sheaf ${\widehat {\mathbb {Z}}}/\mathbb {Z}$ is uniquely divisible by a snake lemma argument. Thus, $\underline {\mathrm {Ext}}^1_v({\widehat {\mathbb {Z}}}/\mathbb {Z},F)$ is also uniquely divisible. The statement follows since we have an exact sequence

\[ \underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},F)\to \underline{\mathrm{Hom}}(\mathbb{Z},F)\to \underline{\mathrm{Ext}}^1_v({\widehat{\mathbb{Z}}}/\mathbb{Z},F). \]

Similarly for the $v$-sheaf $\mathbb {Z}_p/\mathbb {Z}$, which is uniquely $p$-divisible.

Lemma 2.12 The functors $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$ and $\underline {\mathrm {Hom}}(\mathbb {Z}_p,-)$ preserve injectives in the category of abelian sheaves on $\operatorname {Perf}_{K,\tau }$ for $\tau \in \{{\mathrm {\acute {e}t}},v\}$.

Proof. Let $F\to G$ be an injection of abelian sheaves on $\operatorname {Perf}_{K,\tau }$. Let $Q$ be an injective sheaf on $\operatorname {Perf}_{K,\tau }$. Then $F\otimes _{\mathbb {Z}} {\widehat {\mathbb {Z}}}\to G\otimes _{\mathbb {Z}} {\widehat {\mathbb {Z}}}$ is injective as ${\widehat {\mathbb {Z}}}$ is a torsionfree sheaf and thus flat over $\mathbb {Z}$. Hence,

is surjective since $Q$ is injective.

Lemma 2.13 Let $F$ be a strongly topologically torsion v-sheaf. Let $\pi :X\to \operatorname {Spa}(K,K^+)$ be a locally spatial diamond. Then the evaluation map $\mathrm {e}:\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},R^1\pi _{\tau \ast }F)\to R^1\pi _{\tau \ast }F$ admits a splitting for $\tau \in \{{\mathrm {\acute {e}t}},v\}$. In particular, $R^1\pi _{v\ast }F$ is topologically torsion.

Proof. There is a natural equivalence of functors on sheaves $\pi _{\tau \ast }\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)=\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\pi _{\tau \ast }-)$. By Lemma 2.12 this induces Grothendieck spectral sequences which yield a natural map

\[ R^1\pi_{\tau\ast}F=R^1\pi_{\tau\ast}\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},F)\to R^1(\pi_{\tau\ast}\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},-))(F)\to \underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},R^1\pi_{\tau\ast}F). \]

Since this equivalence is also natural in the first entry ${\widehat {\mathbb {Z}}}$, it is compatible with the evaluation map, which means that the above map defines the desired splitting.

2.3 Topologically torsion subgroups of rigid groups

Assume from now on that $K$ is a perfectoid field extension of $\mathbb {Q}_p$, and that the $v$-sheaf $F$ is represented by a rigid group $G$. We recall that by our conventions, this means a group object in the category of adic space of locally finite presentation over $\operatorname {Spa}(K,K^+)$. In this case, the topologically $p$-torsion subgroup $G\langle p^\infty \rangle$ can be described explicitly, and is often represented by an analytic $p$-divisible subgroup in the sense of Fargues: namely, we prove the following extension of a result of Fargues [Far19, Théorème 1.2] which shows that our notion of topologically torsion subsheaves generalises his notion of analytic $p$-divisible subgroups from rigid groups (in the sense of Tate) to general $v$-sheaves.

Proposition 2.14 Let $G$ be a rigid group over $(K,K^+)$. Then we have the following.

1. (i) We have $G\langle p^\infty \rangle =\underline {\mathrm {Hom}}(\mathbb {Z}_p,G)\subseteq G$, and this subsheaf is represented by a rigid open subgroup that is strongly topologically torsion. Its $K$-points are characterised by

   \[ \underline{\mathrm{Hom}}(\mathbb{Z}_p,G)(K,K^+)=\{x\in G(K,K^+)\mid p^n\cdot x\xrightarrow{n\to \infty} 0\}. \]

2. (ii) This open subgroup fits into a left-exact sequence of $v$-sheaves

   \[ 0\to G[p^\infty]\to G\langle p^\infty\rangle\xrightarrow{\log}\mathrm{Lie}(G)\otimes_K \mathbb{G}_a. \]
   If $[p]:G\to G$ is surjective, this sequence is also right-exact.

3. (iii) We have $G^{\mathrm {tt}}=\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},G)$ and this is represented by the open subgroup of $G$

   \[ G^{\mathrm{tt}}=\bigcup_{(N,p)=1} [N]^{-1}(G\langle p^\infty\rangle). \]
   If $K$ is algebraically closed, we can more explicitly describe this as the union
   \[ G^{\mathrm{tt}}=G\langle p^\infty\rangle \cdot \bigcup_{(N,p)=1} G[N](K,K^+)\subseteq G. \]

4. (iv) Assume that $G$ has good reduction, i.e. there is a formal group scheme $\mathfrak G$ that is flat of topologically finite presentation over $K^+$ such that $\mathfrak G^{\mathrm {ad}}_{\eta }=G$. Let $\mathfrak G[p^\infty ]$ be the sheaf on $p$-nilpotent $K^+$-algebras $R$ defined by $\mathfrak G[p^\infty ](R)=\textstyle \varinjlim _{n\in \mathbb {N}} \mathfrak G[p^n](R)$. Then

   \[ G\langle p^\infty\rangle=\mathfrak G[p^\infty]^{\mathrm{ad}}_{\eta} \]
   is the adic generic fibre in the sense of Scholze and Weinstein [SW13, § 2.2]. In particular, $G\langle p^\infty \rangle (K,K^+)$ (respectively, $G^\mathrm {tt}(K,K^+)$) consists of those points of $\mathfrak G(K^+)$ which reduce to a $p^\infty$-torsion point (respectively, torsion point) on the special fibre.

Remark 2.15 The aforementioned Theorem of Fargues asserts that for a (classical) rigid group over $(K,\mathcal {O}_K)$ of characteristic $0$, there exists a rigid open subgroup $U\subseteq G$ such that

\[ |U|_{{\rm Ber}}=\{x\in|G|_{{\rm Ber}}\mid p^n\cdot x\xrightarrow{n\to \infty}0 \}. \]

Proposition 2.14 recovers $U$ and shows that it is equal to $G\langle p^\infty \rangle$. Fargues also shows part (ii) in this case, and part (iv) is his point of view on the $p$-divisible group of $G$ (see [Far19, § 0]).

From this perspective, the new aspects of Proposition 2.14 in the special case of classical rigid groups over $(K,\mathcal {O}_K)$ are the description of $U$ in terms of the $v$-sheaf $\underline {\operatorname {Hom}}(\underline {\mathbb {Z}}_p,-)$ (which crucially uses the language of $v$-sheaves), and the extension to coprime torsion via part (iii).

Remark 2.16 In the second part of Proposition 2.14(iii), we form the disjoint union in the category of adic spaces. This is relevant because in the setting of classical rigid spaces in the sense of Tate, the subspaces $xG\langle p^\infty \rangle$ for $x\in G[N](K)$ typically form a set-theoretic cover of $G$ that is not admissible. In the setting of adic spaces, this cover misses some points of rank two in $G$ that are intentionally not included in $G^\mathrm {tt}$. See also § 2.4.

Example 2.17

1. (i) To obtain an explicit description of $G\langle p^\infty \rangle$, it suffices by part (iv) to find an open subgroup of good reduction $G_0\subseteq G$ such that $[p]^{-1}(G_0)\subseteq G_0$. For example, for $G=\mathbb {G}_m$, such an open subgroup is given by the affine torus $\mathfrak G=\mathbb {G}_{m,\mathcal {O}_K}$. This shows that $\mathbb {G}_m\langle p^\infty \rangle =\widehat {\mathbb {G}}_m\subseteq \mathbb {G}_m$ is the open disc of radius 1 around 1. In particular, by part (iv), we deduce that $\mathbb {G}_m^{\mathrm {tt}}=\mu (K)\widehat {\mathbb {G}}_m$, justifying the description in Example 2.7.

2. (ii) More generally, such an open subgroup exists for semi-abeloid varieties $A$, which are of interest in the context of Picard functors. By Raynaud uniformisation, there is a maximal open subgroup $A^+\subseteq A$ that admits a connected smooth formal model. We then let $G_0$ be the disjoint union of translates of $A^+$ over points in $A[p^\infty ]$. In fact, with this definition, the analogues of parts (i), (iii) and (iv) also hold in characteristic $p$.

3. (iii) If $G=\mathbb {G}_a$, then we cannot find an open subgroup of good reduction $G_0$ such that $[p]^{-1} (G_0)\subseteq G_0$. This is consistent with the fact that the $\mathbb {G}_{a,\mathcal {O}_K}[p^n]$ do not form a $p$-divisible group. Instead, in this case, we have $\mathbb {G}_a\langle p^\infty \rangle =\mathbb {G}_a^{\mathrm {tt}}=\mathbb {G}_a$.

4. (iv) The restriction to the rigid case is necessary: for example, set $G=\mathbb {Z}_l$ for $l\neq p$. Here $G\langle p^\infty \rangle =0 \subseteq G$ is not open, rather it is closed. For part (iv), consider also the example of the formal scheme $\mathfrak G=\varprojlim _{[p]}\mathbb {G}_{m,K^+}$. Its adic generic fibre $G$ is a perfectoid group whose topologically torsion subgroup is given by the open subgroup $\varprojlim _{[p]}\widehat {\mathbb {G}}_m$. This is closely related to the universal cover of $\mu _{p^\infty }$ in the sense of Scholze and Weinstein [SW13, § 3.1]. However, the description of $G\langle p^\infty \rangle$ in terms of torsion points of the special fibre is no longer valid as $\mathfrak G$ is uniquely $p$-divisible, and hence its special fibre is $p$-torsionfree.

Remark 2.18 We note that if $G$ is a rigid group, there is an alternative, ‘analytic’ description of $G^\mathrm {tt}$, as follows. Using the $p$-adic logarithm, one can show that any morphism $\varphi :\mathbb {Z}_p\times T\to G$ in $\underline {\mathrm {Hom}}(\mathbb {Z}_p,G)(T)$ admits an analytic continuation locally. More precisely, for $n\gg 0$, the restriction of $\varphi$ to $p^n\mathbb {Z}_p\times T$ extends uniquely to a $T$-linear homomorphism $\varphi :\mathbb {B}_n\times T\to G$ where $\mathbb {B}_n\subseteq \mathbb {G}_a$ is the closed disc of radius $\leq |p^n|$ with its additive structure. In other words, if $\mathbb {Z}_p(\epsilon )$ denotes for any $\epsilon >0$ the open subgroup of $\mathbb {G}_a$ defined by the union of closed discs of radius $\epsilon$ around $\mathbb {Z}_p\subseteq \mathbb {G}_a(K)$, then we have

\[ G\langle p^\infty\rangle = \varinjlim_{\epsilon>0}\underline{\mathrm{Hom}}(\mathbb{Z}_p(\epsilon),G). \]

Although we do not need this observation in this article, it is useful for other applications.

In light of Proposition 2.14, one can use the topologically $p$-torsion subsheaf to generalise the notion of ‘analytic $p$-divisible groups’ in the sense of Fargues [Far19, § 2 Définition 2]:

Definition 2.19

1. (i) We call a rigid group $G$ over $(K,K^+)$ an analytic $p$-divisible group if $G$ is topologically $p$-torsion (i.e. $G\langle p^\infty \rangle =G$) and $[p]:G\to G$ is surjective.

2. (ii) We call a rigid group $G$ an analytic divisible group if $G$ is topologically torsion (i.e. $G^\mathrm {tt}=G$) and $[n]:G\to G$ is surjective for all $n\in \mathbb {N}$.

Examples of analytic divisible groups include $\mathbb {Q}/\mathbb {Z}$, $\mathbb {G}_a$ and $G^\mathrm {tt}$ for any rigid group $G$ for which $[n]:G\to G$ is surjective for all $n\in \mathbb {N}$, e.g. for abeloid varieties. One can then characterise $G^\mathrm {tt}$ as the maximal analytic divisible subgroup of $G$, and similarly for $G\langle p^\infty \rangle$.

We now start with the proof of Proposition 2.14. For this we use the following result.

Lemma 2.20 Let $G$ be any rigid group over $(K,K^+)$. Then $G(K,K^+)$ is a complete topological group (complete with respect to the uniform structure given by open subgroups).

Proof. To simplify notation, let us just write $G(K)$ for $G(K,K^+)$. We first note that $G(K)$ is a topological group: this is not completely obvious for adic groups since the map $|G\times G|\to |G|\times |G|$ is usually not a bijection. However, the continuous bijection

\[ (G\times G)(K)\to G(K)\times G(K) \]

on $K$-points is indeed a homeomorphism: this follows from the fact that any rigid group admits a neighbourhood basis of $0$ consisting of open rigid subgroups $U\subseteq G$ such that $U\cong \mathbb {B}^d$ as rigid spaces ([Far19, § 1, Corollaire 4] over $(K,\mathcal {O}_K)$, [Heu22a, Corollary 3.7] in general). This also shows that $G(K)$ is Hausdorff.

To see that $G(K)$ is complete, let $(x_n)_{n\in \mathbb {N}}$ be any Cauchy sequence. Then for $n,m\gg 0$, we have $x_n-x_m\in U$ and, thus, $x_n\in x_m+U$. After translating by $x_m$, we may therefore assume $x_n\in U$ for all $n$. Now let $f\in \mathcal {O}^+(U)$ and consider the map

\[ U\times U\to \mathbb{B}, \quad y,\delta\mapsto f(y+\delta)-f(y). \]

For any $\epsilon >0$, let $V_{\epsilon }\subseteq U\times U$ be the pullback of the open ball $\mathbb {B}_{\epsilon }$ of radius $\epsilon$ around $0$. Since $U\times \{0\}\subseteq V_{\epsilon }$, and $U\times \{0\}$ is the tilde limit of $\varprojlim _{n\in \mathbb {N}} U\times \mathbb {B}_{n}$ where $\mathbb {B}_n$ is the ball of radius $|p^n|$, it follows from a standard approximation argument that there is an open subgroup $W_{\epsilon }\subseteq U$ such that $U\times W_{\epsilon }\subseteq V_\epsilon$. For $n,m\gg 0$, we then have $x_m-x_n\in W_\epsilon$ which implies $|f(x_m)-f(x_n)|\leq \epsilon$. Thus, $f(x_m)$ is a Cauchy sequence in $K^+$. It thus makes sense to define

\[ x:\mathcal{O}^+(U)\to K^+,\quad f\mapsto \varprojlim_n f(x_n). \]

One easily checks that this defines the desired limit $x_n\to x\in U(K,K^+)\subseteq G(K,K^+)$.

Remark 2.21 With more work, one can show that $G(K,K^+)$ is a complete topological group for any adic group $G$ over $(K,K^+)$ satisfying the following mild technical assumption: $G$ admits a basis of uniform affine open subspaces $\mathcal {B}$ such that for each $U=\operatorname {Spa}(A,A^+)$ and $V=\operatorname {Spa}(B,B^+)$ in $\mathcal {B}$, the fibre product $U\times _KV$ exists and is affinoid with $\mathcal {O}(U\times _KV)=A\hat {\otimes }_K B$ the tensor product of complete normed $K$-vector spaces. For example, this holds for perfectoid groups. One then obtains the analogous description of $K$-points of $G\langle p^\infty \rangle$.

Proof of Proposition 2.14 We begin by describing the $(K,K^+)$-points of $G\langle p^\infty \rangle$ and $G^\mathrm {tt}$: By Lemma 2.4, we have $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},G)(K)=\operatorname {Hom}_{{\operatorname {cts}}}({\widehat {\mathbb {Z}}},G(K))$. Let $\varphi :{\widehat {\mathbb {Z}}}\to G(K)$ be any continuous homomorphism. This is uniquely determined by the image $x=\varphi (1)$ of $1$. By continuity, since $n!\to 0$ in $\widehat {\mathbb {Z}}$, we have $x^{n!}\to 0$ in $G(K)$.

Conversely, let $x\in G(K)$ be such that $x^{n!}\to 0$. Let $f:\mathbb {Z}\to G(K)$ be the homomorphism defined by $f(1)=x$. For any open subgroup $U\subseteq G(K)$, we have $x^{n!}\in U$ for $n\gg 0$ and, thus, $n!\mathbb {Z}\subseteq f^{-1}(U)$, so $f$ is continuous for the subspace topology on $\mathbb {Z}\subseteq {\widehat {\mathbb {Z}}}$. By the universal property of the completion, $f$ now extends to ${\widehat {\mathbb {Z}}}$ as $G(K)$ is complete by Lemma 2.20.

The case of topological $p$-torsion is analogous. This gives the description of $G\langle p^\infty \rangle (K,K^+)$.

By [Heu22a, Proposition 3.5, Corollary 3.8], there exists an open subgroup $G_1\subseteq G$ of good reduction that admits an open immersion $\log :G_1\hookrightarrow \mathrm {Lie}(G)\otimes _K \mathbb {G}_a$. Let

\[ G_2:=\textstyle\bigcup_{n\in\mathbb{N}} [p]^{-n}(G_1)\subseteq G, \]

this is clearly an open adic subgroup of $G$. We claim that $G_2=G\langle p^\infty \rangle$.

To see that $G\langle p^\infty \rangle \subseteq G_2$, let $T=\operatorname {Spa}(S,S^+)$ be an affinoid perfectoid space over $(K,K^+)$ and let

\[ \varphi:\underline{\mathbb{Z}}_p\times T\to G\times T \]

be any homomorphism over $T$. Then the preimage of $G_1\times T$ contains some neighbourhood $p^n\underline {\mathbb {Z}}_p\times T$ of the identity because $|\mathbb {Z}_p\times T|=\varprojlim |\mathbb {Z}/p^n\mathbb {Z}\times T|=\mathbb {Z}_p\times |T|$. By the definition of $G_2$, this implies that $\varphi$ factors through $G_2$.

To see the converse, let now $\mathfrak G$ be the formal model of $G_1$ and consider the open subgroup

\[ G_0:=\mathfrak G[p^\infty]^{\mathrm{ad}}_\eta\subseteq G_1\subseteq G_2\subseteq G. \]

We now invoke [SW13, Proposition 2.2.2.(ii)], which is written in the case that $K^+=\mathcal {O}_K$, but its proof goes through verbatim also for $(K,K^+)$. This says that the points of $G_0$ on perfectoid $(K,K^+)$-algebras $(R,R^+)$ are given by the sheafification of the presheaf

\[ (R,R^+)\mapsto \{x\in \mathfrak G(R^+)|\text{ for any $n\in \mathbb{N}$ we have }x\bmod p^n\in \mathfrak G[p^\infty](R^+/p^n)\}. \]

Suppose first that we are given any point $\varphi \in G_0(T)$. To prove that this is contained in $G\langle p^\infty \rangle (T)\subseteq G(T)$, we may without loss of generality pass from $T$ to an analytic cover. By the above, we may therefore assume that $\varphi$ has a formal model, i.e. comes from a group homomorphism $\varphi :\operatorname {Spf}(S^+)\to \mathfrak G$ that reduces mod $p^n$ to compatible homomorphisms

\[ \underline{\mathbb{Z}}_p\times \operatorname{Spf}(S^+/p^n)\to \mathfrak G_{K^+/p^n}[p^\infty] \]

for all $n$. Taking the limit over $n$ and passing to the generic fibre, this gives the desired map

\[ \underline{\mathbb{Z}}_p\times T\to G_0=\mathfrak G[p^\infty]^{\mathrm{ad}}_{\eta}. \]

Finally, we observe that given any $x\in G_2(T)$, there is $n$ such that $p^nx\in G_0(T)$. Let $\varphi :\underline {\mathbb {Z}}\times T\to G$ be the homomorphism sending $1\mapsto x$. As we have just shown, its restriction to $p^n\underline {\mathbb {Z}}\times T$ extends uniquely to a map $\widehat {\varphi }:p^n\underline {\mathbb {Z}}_p\times T\to G_0$. Using the short exact sequence

\[ 0\to p^n\underline{\mathbb{Z}}\to p^n\underline{\mathbb{Z}}_p\times \underline{\mathbb{Z}}\to \underline{\mathbb{Z}}_p\to 0 \]

of $v$-sheaves, $\varphi$ now extends uniquely to $\underline {\mathbb {Z}}_p\times T$ by the universal property of the cokernel.

This proves part (i). Part (ii) follows from the open immersion $G_1\hookrightarrow \mathrm {Lie}(G)\otimes _K \mathbb {G}_a$, which can be uniquely extended to $G_2$ by sending $x\in G_0(T)$ with $p^nx\in G_1(T)$ to $\log (x)=p^{-n}\log (p^nx)$. The statement about surjectivity follows as $\mathrm {Lie}(G)\otimes _K \mathbb {G}_a=\bigcup _{n\in \mathbb {N}}p^{-n}\log (G_1)$.

For part (iv), it remains to prove that any morphism $\varphi :\underline {\mathbb {Z}}_p\times T\to G$ factors through $G_0\subseteq G$. Since this is an open subgroup, we see as in the beginning of the proof that there is $n$ such that $\varphi (p^n\underline {\mathbb {Z}}_p\times T)\subseteq G_0$. However, in the case of good reduction, we also have $[p]_G^{-1}(G_0)=G_0$ by the above explicit description of $G_0=\mathfrak G[p^\infty ]_{\eta }^{\mathrm {ad}}$. Thus, $\varphi (\underline {\mathbb {Z}}_p\times T)\subseteq G_0$.

To deduce part (iii), write ${\widehat {\mathbb {Z}}}=\mathbb {Z}_p\times {\widehat {\mathbb {Z}}}^{(p)}$ where ${\widehat {\mathbb {Z}}}^{(p)}=\varprojlim _{(N,p)=1} \mathbb {Z}/N$. It suffices to show the following.

Lemma 2.22 Let $H=\varprojlim _{i\in I} H_i$ be any profinite group for which the order of each $H_i$ is coprime to $p$. Let $G$ be any rigid group over $(K,K^+)$. Then we have

\[ \underline{\mathrm{Hom}}({H},G)=\textstyle\varinjlim_{i\in I}\underline{\mathrm{Hom}}(H_i,G). \]

Proof. Let $f:{H}\times T\to G$ be any homomorphism of adic groups over a perfectoid space $T$. We need to prove that some open subgroup of $H$ gets sent to the identity. In the notation introduced previously, we can therefore assume that $f$ factors through the open subgroup $G_0=\mathfrak G[p^\infty ]^{\mathrm {ad}}_\eta \subseteq G$ and that $f$ admits a formal model ${H}\times \operatorname {Spf}(S^+)\to \mathfrak G$. We claim that $f$ is then trivial. To see this, we may reduce to $T=\operatorname {Spa}(K,K^+)$. Then $f$ corresponds to an inverse system of homomorphisms $H\to \mathfrak G(\mathcal {O}_K/p^n)[p^\infty ]$. Since the right-hand side is discrete, this factors through $H_i$ for some $i$. However, $H_i$ is of order coprime to $p$, so this map is trivial.

This finishes the proof of Proposition 2.14.

2.4 Topological torsion in abeloid varieties

An example of particular interest for our applications to the $p$-adic Simpson correspondence is the case of abeloid varieties, i.e. connected smooth proper rigid groups. For these we have the following curious special case.

Proposition 2.23 Let $A$ be an abeloid variety over $K=\mathbb {C}_p$ or $\mathbb {C}_p^\flat$. Then

\[ A^\mathrm{tt}(K)=A(K). \]

Remark 2.24 This does not mean that the open immersion $A^\mathrm {tt}\to A$ is an isomorphism. Indeed, this is not the case; for example, $A$ is connected whereas $A^\mathrm {tt}$ is an infinite disjoint union of open discs by Proposition 2.14. A closely related phenomenon is that the statement of Proposition 2.23 becomes false for any non-trivial extension of $K$, already for Tate curves.

This difference is relevant to the $p$-adic Simpson correspondence as it explains why the description in Theorem 1.1 in terms of vanishing Chern classes is only valid over $\mathbb {C}_p$.

Proof. If $A$ has good reduction with special fibre $\overline {A}$ over the residue field $\overline {\mathbb {F}}_p$, then by Proposition 2.14(iv), the specialisation map $A(K)\to \overline {A}(\overline {\mathbb {F}}_p)$ induces a short exact sequence

(8)\begin{equation} 0\to A\langle p^\infty\rangle(K)\to A(K)\to \overline{A}(\overline{\mathbb{F}}_p)[\tfrac{1}{p}]\to 0, \end{equation}

where $\overline {A}(\overline {\mathbb {F}}_p)[\tfrac {1}{p}]:=\overline {A}(\overline {\mathbb {F}}_p)\otimes _{\mathbb {Z}}\mathbb {Z}[\tfrac {1}{p}]=\varinjlim _{[p]}\overline {A}(\overline {\mathbb {F}}_p)$. This is an abelian torsion group: indeed, the abelian variety $\overline {A}$ is already defined over a finite extension $\mathbb {F}_q$ of $\mathbb {F}_p$ in $\overline {\mathbb {F}}_p$ and, hence,

\[ \overline{A}(\overline{\mathbb{F}}_p)=\textstyle\varinjlim_{k|\mathbb{F}_q} \overline{A}(k) \]

is a colimit of finite groups, where $k$ ranges through finite extensions of $\mathbb {F}_q$ in $\overline {\mathbb {F}}_p$. By the description of $A^\mathrm {tt}$ in Proposition 2.14(iii), this shows that $A^\mathrm {tt}(K)=A(K)$ in this case.

The general case follows from the case of good reduction via Raynaud uniformisation: By [Lüt16, Theorem 7.6.4], we can write $A=E/M$ for some analytic short exact sequence

\[ 0\to T\to E\to B\to 0 \]

of rigid groups where $B$ is an abeloid variety of good reduction and $T$ is a rigid torus, and where $M\subseteq E(K)$ is a discrete lattice of rank equal to the rank of $T$. It is easy to see that this exact sequence of $E$ becomes split over $B\langle p^\infty \rangle$, hence induces an exact sequence

(9)\begin{equation} 0\to T\langle p^\infty\rangle\to E\langle p^\infty\rangle\to B\langle p^\infty\rangle\to 0. \end{equation}

Let $M\cdot E\langle p^\infty \rangle \subseteq E$ be the open subgroup generated by $M$ and $E\langle p^\infty \rangle$. The composition

(10)\begin{equation} M\cdot E\langle p^\infty\rangle\to E\to A \end{equation}

factors through $A\langle p^\infty \rangle$. Recall that the cokernel of $A\langle p^\infty \rangle \to A^\mathrm {tt}$ is torsion by Proposition 2.14(iii), so to prove that $A^\mathrm {tt}(K)=A(K)$, it suffices to prove that the composition (10) is surjective on $K$-points after tensoring with $\mathbb {Q}$. Hence it suffices to prove the following.

Lemma 2.25 Let $A=E/M$ be an abeloid variety over $\mathbb {C}_p$ or $\mathbb {C}_p^\flat$. Then

\[ (E\langle p^\infty\rangle(K)\cdot M)\otimes \mathbb{Q}=E(K)\otimes \mathbb{Q}. \]

Proof. As we noted previously, the group $\overline B(\overline {\mathbb {F}}_p)$ is torsion, and thus $\overline B(\overline {\mathbb {F}}_p)\otimes \mathbb {Q}=0$. By tensoring with $\mathbb {Q}$ the short exact sequence (8) in the case of $A=B$, this proves the statement in the case of good reduction, where the lattice $M$ is trivial.

The same argument shows that the inclusion $(1+\mathfrak {m}_K)\otimes \mathbb {Q}\to \mathcal {O}_{\mathbb {C}_p}^\times \otimes \mathbb {Q}$ is an isomorphism as $\overline {\mathbb {F}}_p^\times$ is torsion. Consequently, the valuation on $K$ defines a short exact sequence

\[ 0\to (1+\mathfrak{m}_K)\otimes \mathbb{Q}\to K^\times\otimes \mathbb{Q}\to \mathbb{Q}\to 0. \]

If $M^\vee =\operatorname {Hom}(T,\mathbb {G}_m)$ denotes the character lattice of $T$, we obtain from this and the pairing $M^\vee \times T(K)\to K^\times$ an exact sequence

\[ 0\to T\langle p^\infty\rangle(K)\otimes \mathbb{Q}\to T(K)\otimes \mathbb{Q}\rightarrow \operatorname{Hom}(M^\vee,\mathbb{Q})\to 0. \]

Now since $B\langle p^\infty \rangle (K)\otimes \mathbb {Q}=B(K)\otimes \mathbb {Q}$, we can use (9) to extend this to an exact sequence

\[ 0\to E\langle p^\infty\rangle(K)\otimes \mathbb{Q}\to E(K)\otimes \mathbb{Q}\rightarrow \operatorname{Hom}(M^\vee,\mathbb{Q})\to 0. \]

Finally, we consider the composition

\[ M\to E(K)\to \operatorname{Hom}(M^\vee,\mathbb{Q}), \]

which is injective by duality theory of abeloids (see [Lüt16, § 6.3, Proposition 6.1.8.c(ii)]). Consequently, tensoring with $\mathbb {Q}$ turns it into an injective homomorphism of $\mathbb {Q}$-vector spaces of the same dimension $\mathrm {rk} M=\mathrm {rk} T=\mathrm {rk} M^\vee$ and, hence, into an isomorphism. This shows that $E\langle p^\infty \rangle (K)$ and $M$ generate all of $E(K)$ after tensoring with $\mathbb {Q}$.

3. Pro-finite-étale line bundles in families

Let $K$ be an algebraically closed non-archimedean field over $\mathbb {Q}_p$ with ring of integral elements $K^+$. Let $\pi :X\to \operatorname {Spa}(K,K^+)$ be a connected smooth proper rigid space over $K$. Based on the preparations of the last section as well as the prequel articles [Heu21a, Heu22b], the goal of this section is to answer the following question in the case of line bundles.

Question 3.1 Which vector bundles on $X$ are trivialised by pro-finite-étale covers of $X$?

As explained in detail in the introduction, this question is of interest in the $p$-adic Simpson correspondence, as it is known to lead to the answer of Question 1.6 in various situations, including the case of Higgs field $0$, the case of line bundles and of abelian varieties [Wür23, MW23, Heu22b, HMW23]. Our aim is to give a complete answer to Question 3.1 in the case of line bundles, in terms of the topologically torsion subgroup of the Picard variety. This gives a more geometric, more explicit, and more conceptual description than that we previously gave in [Heu22b, § 5]. Moreover, it naturally leads to a rigid moduli space of pro-finite-étale line bundles, without assuming that the rigid Picard functor is representable.

3.1 The rigid analytic character variety of $\mathbb {G}_m$

Our description of pro-finite-étale $v$-line bundles will be in terms of the $p$-adic analogue of the character variety, which we can define by an application of Proposition 2.14.

Definition 3.2 Let $X$ be any connected smooth proper rigid space over $(K,K^+)$. Let $x\in X( K)$ be a base point and let $\pi _1(X):=\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$ be the étale fundamental group of $X$, a profinite group. Then the continuous character variety of $X$ is the $v$-sheaf on $\operatorname {Perf}_{K,v}$

\[ \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m), \]

where $\pi _1(X)=\underline {\pi _1(X)}$ is considered as a profinite $v$-sheaf (Definition 2.2). Explicitly, the displayed sheaf sends $T\in \operatorname {Perf}_K$ to the set of $T$-linear homomorphisms $\underline {\pi _1(X)}\times T\to \mathbb {G}_m$, which we easily verify to be in bijection with the set of continuous group homomorphisms

\[ \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1(X),\mathcal{O}^\times(T)). \]

Lemma 3.3 The continuous character variety is representable by a rigid analytic group whose identity component is non-canonically isomorphic to $\widehat {\mathbb {G}}_m^d$ for $d=\dim _{\mathbb {Q}_p}H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Q}_p)$ (here $\widehat {\mathbb {G}}_m$ is the open unit disc around $1$). Its group of connected components is torsion.

If $\pi _1(X)$ is the profinite completion of a finitely generated group (e.g. if $X$ is projective), then the proof shows that $\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ is isomorphic to a finite disjoint union of copies of $(\mathbb {G}_m^{\mathrm {tt}})^d$. Here the disjoint union accounts for torsion in the Néron–Severi group.

Proof. Any continuous character $\pi _1(X)\to \mathcal {O}^\times (Y)$ for any perfectoid space $Y$ factors through the maximal abelian quotient $\pi ^{\mathrm {ab}}$ of $\pi _1(X)$, so we have

\[ \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)=\underline{\mathrm{Hom}}(\pi^{\mathrm{ab}},\mathbb{G}_m). \]

Let $T$ be the maximal torsionfree pro-$p$-quotient of $\pi ^{\mathrm {ab}}$. By [Heu22b, Corollary 4.11], $T$ is a finite free $\mathbb {Z}_p$-module of rank $d$ (the finiteness is based on [Sch13, Theorem 1.1]). Thus,

\[ \pi^{\mathrm {ab}}=T\times M\times N \]

for some $p^\infty$-torsion group $M$ and some profinite group $N=\varprojlim N_i$ where each $N_i$ has order coprime to $p$. Hence,

\begin{align*} \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)&=\underline{\mathrm{Hom}}(T,\mathbb{G}_m)\times \underline{\mathrm{Hom}}(M,\mathbb{G}_m) \times \underline{\mathrm{Hom}}(N,\mathbb{G}_m)\\ &\cong\widehat{\mathbb{G}}_m^d\times \varinjlim\underline{\mathrm{Hom}}(N_i\times M,\mathbb{G}_m) \end{align*}

by Proposition 2.14 and Lemma 2.22.

3.2 Diamantine Picard functors

The second ingredient in our description of pro-finite-étale line bundles are the diamantine Picard functors introduced in [Heu21a]. We therefore begin the discussion by recalling the definition and some basic properties.

Definition 3.4 Let $\pi :Y\to \operatorname {Spa}(K,K^+)$ be any locally spatial diamond and consider the associated morphism of big étale sites $\pi _{{\mathrm {\acute {e}t}}}:\mathrm {LSD}_{Y,{\mathrm {\acute {e}t}}}\to \operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. Then we call

\[ \mathbf{Pic}_{Y,{\mathrm{\acute{e}t}}}:=R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m:\operatorname{Perf}_{K,{\mathrm{\acute{e}t}}}\to \mathrm{Ab} \]

the étale diamantine Picard functor, where $\mathrm {Ab}$ is the category of abelian groups. Explicitly, $\mathbf {Pic}_{Y,{\mathrm {\acute {e}t}}}$ is the étale sheafification of the functor on $\operatorname {Perf}_K$ that sends $T\mapsto \operatorname {Pic}_{{\mathrm {\acute {e}t}}}(Y\times T)$.

Second, there is also a $v$-Picard functor which instead parametrises $v$-line bundles, namely

\[ \mathbf{Pic}_{Y,v}:=R^1\pi_{v\ast}\mathbb{G}_m:\operatorname{Perf}_{K,v}\to \mathrm{Ab}, \]

the $v$-sheafification of $T\mapsto \operatorname {Pic}_{v}(Y\times T)$ where $T$ ranges through perfectoid spaces over $K$.

We are most interested in the case that $Y=X$ is a smooth proper rigid space as before. In this case, the two main results of [Heu21a] about these functors are as follows: we first proved that $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is the ‘diamondification’ of the classical rigid analytic Picard functor defined on smooth rigid analytic test objects [Heu21a, Theorem 1.1]. In particular, if the latter is represented by some rigid group $G$ (which conjecturally is always the case, and this is known, e.g., if $X$ is projective), then $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by $G^\diamondsuit$. We therefore drop the additional $-^\diamondsuit$ used in [Heu21a] from notation and write $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ instead of $\mathbf {Pic}^\diamondsuit _{X,{\mathrm {\acute {e}t}}}$.

Second, we proved the following geometric version of the main theorem of [Heu22b].

Theorem 3.5 [Heu21a, Theorem 2.7 and Corollary 2.9]

There is a natural short exact sequence of abelian sheaves on $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$, functorial in $X$,

(11)\begin{equation} 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\to \mathbf{Pic}_{X,v}\xrightarrow{\mathrm{HTlog}} H^0(X,\Omega^1_X(-1))\otimes_K \mathbb{G}_a\to 0. \end{equation}

In particular, this shows that $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is already a $v$-sheaf and that $\mathbf {Pic}_{X,v}$ is represented by a rigid group whenever $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is.

Note that in terms of the language introduced in the introduction, the last term in (11) can be interpreted as the $p$-adic Hitchin base $\mathcal {A}$ in the context of line bundles.

3.3 The pro-finite-étale universal cover

To make the connection to Question 3.1, we first reformulate the question slightly: recall that we have chosen a base point $x\in X(K)$. We consider the universal pro-finite-étale cover of $X$, defined as the spatial diamond

\[ \widetilde \pi:\widetilde X:=\varprojlim_{X'\to X}X'\to \operatorname{Spa}(K), \]

where the index category is given by connected finite étale covers $(X',x')\to (X,x)$ with $x'\in X'(K)$ a lift of $x\in X(K)$. This is a pro-finite-étale $\pi _1(X):=\pi ^{{\mathrm {\acute {e}t}}}_1(X,x)$-torsor. We refer to [Heu22b, Definition 3.8] for further background.

By [Heu22b, Lemma 4.8], we see that a vector bundle on $X$ is pro-finite-étale if and only if it becomes trivial after pullback to $\widetilde X\to X$. Moreover, we argued in [Heu22b, § 5.2] that $\widetilde X\to X$ plays a similar role for the $p$-adic Simpson correspondence as the complex universal cover plays in the complex Simpson correspondence: there is an equivalence of categories

\begin{align}\bigg\{\begin{array}{@{}c@{}l}\text{pro-finite-}{{\mathrm{\acute{e}tale}}}\\\text{$v$-vector bundles on $X$} \end{array}\bigg\}&{\tilde{\to}} \bigg\{\begin{array}{@{}c@{}l}\text{continuous representations of $\pi_1^{{\mathrm{\acute{e}t}}}(X,x)$}\\\text{on finite-dimensional $K$-vector spaces}\end{array}\bigg\}\\ V&\mapsto V(\widetilde X) \end{align}

since $\widetilde X\to X$ is a $\pi _1(X)$-torsor and $\mathcal {O}(\widetilde X)=K$.

In order to describe the left-hand side for line bundles, we now use the diamantine Picard functor $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ of the universal cover. Namely, the main technical result of this article is that we can describe pro-finite-étale line bundles in terms of the topologically torsion subsheaf as defined in § 2 applied to the diamantine Picard functor of $X$:

\[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^\mathrm{tt}:=(\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}})^\mathrm{tt}. \]

Here, we note that it makes sense to apply $-^\mathrm {tt}$ to $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ since this a $v$-sheaf by Theorem 3.5. Moreover, $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$ has a close relation to the character variety from Definition 3.2.

Theorem 3.6 Let $\pi :X\to \operatorname {Spa}(K,K^+)$ be a connected smooth proper rigid space.

1. (i) There is a short exact sequence of abelian sheaves on $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$

   \[ 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^\mathrm{tt}\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\to \mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}}, \]
   in which the first term can equivalently be described as $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}=R^1\pi _{{\mathrm {\acute {e}t}}\ast }(\mathbb {G}_m^\mathrm {tt})$.

2. (ii) In the $v$-topology, we similarly have a short exact sequence

   \[ 0\to \mathbf{Pic}_{X,v}^\mathrm{tt}\to \mathbf{Pic}_{X,v}\to \mathbf{Pic}_{\widetilde X,v}, \]
   in which the first term can be naturally identified with the character variety
   \[ \mathbf{Pic}_{X,v}^\mathrm{tt}=R^1\pi_{v\ast}(\mathbb{G}_m^\mathrm{tt})=\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m). \]

We prove Theorem 3.6 over the course of this section. First, we note that this gives the desired answer to Question 3.1 for line bundles: the pro-finite-étale line bundles on $X$ are precisely the topologically torsion $K$-points of the (classical) rigid-analytic Picard variety.

Corollary 3.7 Assume that the rigid analytic Picard functor of $X$ is represented by a rigid group $G$. Then there is a left exact sequence

\[ 0\to G(K)^\mathrm{tt}\to \operatorname{Pic}_{{\mathrm{\acute{e}t}}}(X)\to \operatorname{Pic}_{{\mathrm{\acute{e}t}}}(\widetilde X), \]

where $G(K)^\mathrm {tt}\subseteq G(K)$ is the subgroup of elements $x$ such that $x^{n!}\to 1$ for $n\to \infty$.

Proof. By [Heu21a, Theorem 1.1], the assumption implies that also $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by the rigid group $G$. The result thus follows from Theorem 3.6(i) by evaluating at $K$ and using that $G^\mathrm {tt}(K)=G(K)^\mathrm {tt}$ by Proposition 2.14(i) and (iii).

Remark 3.8

1. (i) If $K=\mathbb {C}_p$ and the identity component $G^0$ is abeloid, then by Proposition 2.23, $G^\mathrm {tt}(\mathbb {C}_p)=G^\tau (\mathbb {C}_p)$ is generated by $G^0(\mathbb {C}_p)$ and torsion in the Néron–Severi group. In particular, these are then precisely the line bundles in $\operatorname {Pic}(X)$ with vanishing Chern classes. However, this is no longer true over extensions of $\mathbb {C}_p$.

2. (ii) Even without assuming any representability results, $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is always a small $v$-sheaf (this follows from [Heu22c, Theorem 7.13]), hence $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}(K)$ always has the natural structure of a topological space by [Sch18, Definition 12.8]. One can then still describe $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(K)$ as those $x$ in $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}(K)$ such that $x^{n!}\to 1$ for $n\to \infty$.

3. (iii) In general, the sequence is not right-exact: if $X$ is an abelian variety with good supersingular reduction $\overline {X}$, then $\operatorname {Pic}(\widetilde X)=\operatorname {Pic}(\overline {X})\otimes \mathbb {Q}$ by [Heu21b, Theorem 4.1].

4. (iv) We cannot expect $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ to be represented by an adic group: if $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ and $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ were both representable by adic groups, then the kernel of $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}\to \mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ would be closed, a contradiction to Proposition 2.14 if $\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ is a rigid group of dimension $>0$. In fact, we show in [Heu21b, § 6.5] that $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ is typically not even a diamond.

3.4 Relative universal property of the universal cover

The first step for the proof of Theorem 3.6 is to show that $\mathbb {G}_m^{\mathrm {tt}}$-torsors become trivial on the pro-finite-étale universal cover $\widetilde X\to X$. This is part of the following analogue of the statement that the complex universal cover is simply connected. We recall that we write $\widetilde \pi :\widetilde X\to \operatorname {Spa}(K)$ for the structure map.

Proposition 3.9 Let $\mathcal {F}$ be any one of the $v$-sheaves $\mathcal {O}^{+a}/p^k$, $\mathcal {O}^{+a}$, $\mathcal {O}$, $\mathcal {O}^{\flat + a}$, $\mathcal {O}^\flat$, $\mathbb {G}_m\langle p^\infty \rangle$, $\mathbb {G}_m^{\mathrm {tt}}$, or $\mathbb {Z}/N\mathbb {Z}$, where $k,N\in \mathbb {N}$. Then for any affinoid perfectoid space $Y$ over $K$ and for $n\in \{0,1\}$,

\[ H^n_{{\mathrm{\acute{e}t}}}(\widetilde X\times Y,\mathcal{F})=H^n_{{\mathrm{\acute{e}t}}}(Y,\mathcal{F})=H^n_{v}(Y,\mathcal{F})=H^n_{v}(\widetilde X\times Y,\mathcal{F}). \]

In particular, $\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathcal {F}=\mathcal {F}=\widetilde \pi _{v\ast }\mathcal {F}$ and $R^1\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathcal {F}=0=R^1\widetilde \pi _{v\ast }\mathcal {F}$ on $\operatorname {Perf}_K$.

Remark 3.10 The restriction to $n\in \{0,1\}$ is necessary in general: the proposition does not hold for $n=2$ for any of the sheaves in the example of $X=\mathbb {P}^1=\widetilde X$ and $Y{=}\operatorname {Spa}(K)$.

Proof. This is a relative version of [Heu22b, Proposition 3.10], and the technical results of [Heu21a, § 4] enable us to essentially follow the same line of argument: we start with $\mathcal {F}=\mathcal {O}^+/p^k$. By [Heu21a, Proposition 4.12.2], which we recall as Lemma 3.11,

\[ H^1_v(\widetilde X\times Y,\mathcal{O}^+/p^k)\stackrel{a}= \varinjlim_{X'\to X}H^1_{{\mathrm{\acute{e}t}}}(X'\times Y,\mathcal{O}^+/p^k), \]

where the $X'$ are as in the definition of $\widetilde X$. By [Heu21a, Corollary 4.6], this equals

\[ \cdots\stackrel{a}= \varinjlim_{X'\to X} H^1_{\mathrm{\acute{e}t}}(X',\mathbb{Z}/p^k)\otimes \mathcal{O}^+(Y)/p^k=0, \]

which vanishes because every class in $H^1_{\mathrm {\acute {e}t}}(X',\mathbb {Z}/p^k)$ is trivialised by a connected finite étale cover of $X'$ and, thus, of $X$. This gives the case of $n=1$.

The case $n=0$ follows from Lemma 3.11 and [Heu21a, Proposition 4.2.2.(iii)] which says that

\[ H^0(X'\times Y,\mathcal{O}^+/p^k)\stackrel{a}= H^0(Y,\mathcal{O}^+/p^k). \]

Next, consider $\mathcal {F}=\mathcal {O}^+$: the last equation implies that $R^1\varprojlim _{k\in \mathbb {N}} H^0(\widetilde X\times Y,\mathcal {O}^+/p^k)\stackrel {a}= 0$, so we deduce from the fact that the $v$-site is replete and [BS15, Proposition 3.1.10] that

\begin{align*} H^1_v(\widetilde X\times Y,\mathcal{O}^+)\stackrel{a}= \varprojlim_{k\in \mathbb{N}} H^1_v(\widetilde X\times Y,\mathcal{O}^+/p^k)\stackrel{a}= 0. \end{align*}

The case of $\mathcal {O}$ follows. A similar limit argument gives the cases of $\mathcal {O}^{\flat +a}$ and then $\mathcal {O}^\flat$.

Since we have an injection $H^1_{{\mathrm {\acute {e}t}}}(\widetilde X\times Y,\mathcal {F})\hookrightarrow H^1_{v}(\widetilde X\times Y,\mathcal {F})$, the result for $H^1_{{\mathrm {\acute {e}t}}}(\widetilde X\times Y,\mathcal {F})$ follows from the respective statements for $H^1_{v}(\widetilde X\times Y,\mathcal {F})$ for each of these sheaves.

For $\mathcal {F}=\mathbb {Z}/N\mathbb {Z}$, we know that étale and $v$-topology agree. By [Sch18, Proposition 14.9],

\[ H^n_{{\mathrm{\acute{e}t}}}(\widetilde X\times Y,\mathbb{Z}/N\mathbb{Z})=\varinjlim H^n_{{\mathrm{\acute{e}t}}}(X'\times Y,\mathbb{Z}/N\mathbb{Z}). \]

For $n=0$, it follows from [Heu21a, Corollary 4.8] that $\widetilde \pi _{\ast }\mathbb {Z}/N\mathbb {Z}=\mathbb {Z}/N\mathbb {Z}$. To see the case of $n=1$, it thus suffices by the Leray sequence to prove that $R^1\widetilde \pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {Z}/N\mathbb {Z}=0$, which follows from the same cited result in the colimit over the $X'$.

Finally, the case of $\mathbb {G}_m\langle p^\infty \rangle$ follows from that of $\mu _{p^\infty }\cong \varinjlim \mathbb {Z}/p^k\mathbb {Z}$ (as $K$ is algebraically closed) and that of $\mathcal {O}$ by the logarithm sequence, and similarly for $\mathbb {G}_m^\mathrm {tt}$ where we also include coprime-to-$p$ torsion. This also shows that étale and $v$-cohomology agree in this case.

Lemma 3.11 Let $Y$ be any perfectoid space over $K$ and let $\widetilde X=\varprojlim _{i\in I} X_i$ be a diamond which is a limit of smooth quasi-compact quasi-separated (qcqs) rigid spaces over $K$ with finite étale transition maps. Then for the $v$-sheaves $\mathcal {F}=\mathcal {O}^{+a}/p$ or $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}$, we have for $n\in \{0,1\}$:

\[ H^n_{v}(\widetilde X\times Y,\mathcal{F})=\textstyle\varinjlim_{i \in I} H^n_{{\mathrm{\acute{e}t}}}(X_i\times Y,\mathcal{F}). \]

Moreover, both sides stay the same when we exchange the $v$-topology for the étale topology.

Proof. For $\mathcal {F}=\mathcal {O}^{+a}/p$ and $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle$ this is [Heu21a, Proposition 4.12.1 and 2] (where the latter sheaf was denoted by $\overline {\mathcal {O}}^{\times }$). The case of $\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}$ follows by tensoring with $\mathbb {Q}$ since $\mathbb {G}_m/\mathbb {G}_m^{\mathrm {tt}}=(\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle )\otimes _{\mathbb {Z}} \mathbb {Q}$, see [Heu22b, Lemma 2.16].

Corollary 3.12 The natural map $\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}\to \mathbf {Pic}_{\widetilde X,v}$ is injective.

Proof. By Proposition 3.9, we have $\widetilde \pi _{\ast }\mathcal {O}=\mathcal {O}$ and, thus, $\widetilde \pi _{\ast }\mathbb {G}_m=\mathbb {G}_m$. We can therefore apply [Heu21a, Lemma 4.13], which gives the following commutative diagram with short exact rows.

As the first column is an isomorphism by [KL16, Theorem 3.5.8], and the middle column is clearly injective, we can deduce that the last column is injective as well.

Remark 3.13 We do not know whether the map in Corollary 3.12 is an isomorphism in general. Although this is true for curves, it is certainly not always true that $v$-vector bundles on $\widetilde X$ agree with étale vector bundles, as the example of $X=\widetilde X=\mathbb {P}^1$ shows.

Remark 3.14 An alternative proof of Proposition 3.9 in the case of $\mathbb {Z}/N\mathbb {Z}$ and $n=1$ would be to show that $(\widetilde X\times Y)_{{\mathrm {f\acute {e}t}}}=Y_{{\mathrm {f\acute {e}t}}}$. One could deduce this from the following rigid analogue of a well-known algebraic statement: let $X$ be a connected proper rigid space and $Y$ any connected reduced rigid space. Then is the natural map $\pi ^{{\mathrm {\acute {e}t}}}_1(X\times Y)\to \pi _1^{{\mathrm {\acute {e}t}}}(X)\times \pi ^{{\mathrm {\acute {e}t}}}_1(Y)$ an isomorphism? We suspect that one could see this like in [SGA1, X Corollaire 1.7], or using [SW20, § 16]. By an approximation argument, one could deduce that $(\widetilde X\times Y)_{{\mathrm {f\acute {e}t}}}=Y_{{\mathrm {f\acute {e}t}}}$.

3.5 Topologically torsion line bundles

Next, we show that any pro-finite-étale line bundle admits a reduction of structure group from $\mathbb {G}_m$ to $\mathbb {G}_m^\mathrm {tt}$. For this, we first show the following result.

Lemma 3.15 For any perfectoid space $Y$, there is for $n\in \{0,1\}$ a natural isomorphism

\[ H^n_{v}(X\times Y,\mathbb{G}_m/\mathbb{G}_m^\mathrm{tt}){\tilde{\to}} H^n_{v}(\widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^\mathrm{tt})^{\pi_1(X)}. \]

Moreover, both sides remain the same when we exchange the $v$-topology for the étale topology.

Proof. We form the Cartan–Leray spectral sequence of the $\pi _1(X)$-torsor $\widetilde X\times Y\to X\times Y$ for the sheaf $\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$, see [Heu22b, Proposition 2.8]. Endow $H^n_v(\widetilde X\times Y,\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt})$ with the discrete topology, then by Lemma 3.11, we have for any profinite group $G$:

\[ H^n_v(G\times \widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^\mathrm{tt})=\operatorname{Map}_{{\operatorname{cts}}}(G,H^n_v(\widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^\mathrm{tt})). \]

For $n=0$, the lemma follows by setting $G=\pi _1(X)$ and using the $v$-sheaf property of $\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$. For $n=1$, this equation ensures that the conditions of [Heu22b, Proposition 2.8.2] are satisfied. Setting $G:=\pi _1(X)$ and $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$, we thus obtain an exact sequence

\[ 0\to H^1_{{\operatorname{cts}}}(G,\mathcal{F}(\widetilde X\times Y))\to H^1_v(X\times Y,\mathcal{F})\to H^1_v(\widetilde X\times Y,\mathcal{F})^{G}\to H^2_{{\operatorname{cts}}}(G,\mathcal{F}(\widetilde X\times Y)). \]

Since $G=\pi _1(X)$ is profinite and $\mathcal {F}=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$ is a sheaf of $\mathbb {Q}$-vector spaces, the outer two groups vanish by [NSW08, Proposition 1.6.2.c]. This gives the desired statement for the $v$-topology. The étale case follows from this by Lemma 3.11 and [Heu21a, Proposition 4.12.1], or alternatively from the more general [Heu22a, Proposition 4.8].

Lemma 3.16 [Heu21a, Lemma 4.11.2]

We have $\pi _{\tau \ast }(\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt})=\mathbb {G}_m/\mathbb {G}_m^\mathrm {tt}$ for $\tau \in \{{\mathrm {\acute {e}t}},v\}$.

Proof. The reference shows this for $\mathbb {G}_m/\mathbb {G}_m\langle p^\infty \rangle$. The lemma follows by tensoring with $\mathbb {Q}$.

We can now complete the first steps of the proof of Theorem 3.6.

Proof of Theorem 3.6 Let $\tau \in \{{\mathrm {\acute {e}t}},v\}$ and consider the following morphism of exact sequences.

Here the top left entry vanishes by Proposition 3.9. The right vertical morphism is injective by Lemma 3.15. The bottom left morphism is injective by Lemma 3.16.

This shows that we have a left-exact sequence:

(12)\begin{equation} 0\to R^1\pi_{\tau\ast}\mathbb{G}_m^{\mathrm{tt}}\to \mathbf{Pic}_{X,\tau} \to \mathbf{Pic}_{\widetilde X,\tau}. \end{equation}

We first consider $\tau ={\mathrm {\acute {e}t}}$. Note that (12) combines with Theorem 3.5 and Corollary 3.12 to show that $R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}$ is the kernel of a morphism of $v$-sheaves, hence it is itself a $v$-sheaf. For Theorem 3.6(i), it remains to prove that $R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$. This relies on the following key calculation, which crucially uses that our Picard functors use perfectoid test objects.

Proposition 3.17 We have $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}})=1$.

Proof. For any affinoid perfectoid space $Y$ over $K$, a section $f\in \underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},\mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}})(Y)$ is by definition of $\underline {\mathrm {Hom}}$ a morphism of sheaves on $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$

\[ f:{\widehat{\mathbb{Z}}}\times Y\to \mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}} \]

making the following diagram commute.

Here, in each row, $m$ denotes the multiplication morphism of abelian sheaves on $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. Denote by $q_1$ the morphism sending a map $f:{\widehat {\mathbb {Z}}}\times Y\to \mathbf {Pic}_{\widetilde X,{\mathrm {\acute {e}t}}}$ to the composition $m\circ (f\times f)$ in the diagram, and by $q_2$ the map sending $f$ to $f\circ m$, then we can reformulate this description as saying that

(13)\begin{equation} \underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},\mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}})(Y)=\mathrm{eq} \big(\mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}}({\widehat{\mathbb{Z}}}\times Y)\mathrel{\mathop{\rightrightarrows}^{q_1}_{q_2}} \mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}}({\widehat{\mathbb{Z}}}^2\times Y)\big). \end{equation}

We now use that for any $n\in \mathbb {N}$, we have, by Lemma 3.18 applied to $F=\mathbb {G}_m$ and the composition $\widetilde X\times Y\times {\widehat {\mathbb {Z}}}^n\to Y\times {\widehat {\mathbb {Z}}}^n \to Y$, a natural identification

\[ \mathbf{Pic}_{\widetilde X,{\mathrm{\acute{e}t}}}({\widehat{\mathbb{Z}}}^n\times Y)=\mathbf{Pic}_{{\widehat{\mathbb{Z}}}^n\times\widetilde X,{\mathrm{\acute{e}t}}}( Y). \]

It follows that the right-hand side of (13) equals the sheafification of the presheaf

\[ Y\mapsto \mathrm{eq} \big(\operatorname{Pic}_{{\mathrm{\acute{e}t}}}({\widehat{\mathbb{Z}}}\times \widetilde X\times Y)\rightrightarrows \operatorname{Pic}_{{\mathrm{\acute{e}t}}}({\widehat{\mathbb{Z}}}^2\times \widetilde X\times Y)\big) \]

on $\operatorname {Perf}_{K,{\mathrm {\acute {e}t}}}$. We claim that this sheaf vanishes: let $g$ be the map defined as the composition

\[ g: {\widehat{\mathbb{Z}}}^n\times \widetilde X \xrightarrow{\pi_1}{\widehat{\mathbb{Z}}}^n\xrightarrow{r} \operatorname{Spa}(K), \]

where $\pi _1$ is the projection to the first factor and $r$ is the structure map. Invoking Lemma 3.18 again, we deduce that

\[ R^1g_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}}=r_{{\mathrm{\acute{e}t}}\ast} R^1 \pi_{1,{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}}. \]

However, $R^1 \pi _{1,{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=1$ by Proposition 3.9. Hence, $R^1g_{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}=1$. It therefore suffices to prove that the presheaf on $\operatorname {Perf}_{K}$ given by

(14)\begin{equation} Y\mapsto \mathrm{eq}\big(H^1_{{\mathrm{\acute{e}t}}}(\widehat{\mathbb{Z}}\times \widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^{\mathrm{tt}})\mathrel{\mathop{\rightrightarrows}^{q_1}_{q_2}} H^1_{{\mathrm{\acute{e}t}}}(\widehat{\mathbb{Z}}^2\times \widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^{\mathrm{tt}})\big) \end{equation}

is trivial. For this, we use that by Lemma 3.11, we have for any $n\in \mathbb {N}$ an identification

\[ H^1_{{\mathrm{\acute{e}t}}}(\widehat{\mathbb{Z}}^n\times \widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^{\mathrm{tt}})=\operatorname{Map}_{{\operatorname{lc}}}(\widehat{\mathbb{Z}}^n,H^1_{{\mathrm{\acute{e}t}}}(\widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^{\mathrm{tt}})), \]

where $\operatorname {Map}_{{\operatorname {lc}}}$ denotes the set of locally constant maps. Translating the morphisms $q_1$, $q_2$ in (14) via this identification, we see that the presheaf (14) is precisely given by sending $Y$ to

\[ \operatorname{Hom}_{{\operatorname{lc}}}(\widehat{\mathbb{Z}},H^1_{{\mathrm{\acute{e}t}}}(\widetilde X\times Y,\mathbb{G}_m/\mathbb{G}_m^{\mathrm{tt}})). \]

However, the second argument is a $\mathbb {Q}$-vector space, so this group is trivial, as desired.

Lemma 3.18 For any spatial diamonds $X$ and $Y$ over $K$ and any profinite set $S$, write

\[ X\times Y\times S\xrightarrow{\pi_1} Y\times S\xrightarrow{\pi_2} Y \]

for the projections. Then for any abelian sheaf $F$ on $\mathrm {LSD}_{K,{\mathrm {\acute {e}t}}}$ and any $n\geq 0$, we have

\[ R^n(\pi_2\circ\pi_1)_{{\mathrm{\acute{e}t}}\ast}F=\pi_{2,{\mathrm{\acute{e}t}}\ast}R^n\pi_{1,{\mathrm{\acute{e}t}}\ast}F. \]

Proof. We claim that the functor $\pi _{2,{\mathrm {\acute {e}t}}\ast }$ from abelian sheaves on $(Y\times S)_{\mathrm {\acute {e}t}}$ to abelian sheaves on $Y_{\mathrm {\acute {e}t}}$ is right-exact. Indeed, let $F\to G$ be a surjection of sheaves on $(Y\times S)_{\mathrm {\acute {e}t}}$ and let $\alpha \in \pi _{2,{\mathrm {\acute {e}t}}\ast }G(Y)=G(Y\times S)$, then there exists an étale cover $T\to Y\times S$ such that the image of $\alpha$ in $G(T)$ can be lifted to $F(T)$. Write $S=\varprojlim S_i$ for some finite sets $S_i$, then $Y\times S=\varprojlim Y\times S_i$ in the category of diamonds. It follows using [Sch18, Proposition 11.23] that the étale cover $T\to Y\times S$ can be refined by one of the form $(Y'\times U_j\to Y\times S)_{j\in J}$ where $Y'\to Y$ is an étale cover of $Y$ and $\sqcup _{j\in J} U_j=S$ is a disjoint open cover of $S$. Hence, $\alpha$ also lifts to

\[ \textstyle\prod_{j\in J}F(Y'\times U_j)=F(Y'\times S)=\pi_{2,{\mathrm{\acute{e}t}}\ast}F(Y'). \]

This shows that $\pi _{2,{\mathrm {\acute {e}t}}\ast }F\to \pi _{2,{\mathrm {\acute {e}t}}\ast }G$ is still surjective. It follows from this right-exactness that $R\pi _{2,{\mathrm {\acute {e}t}}\ast }=\pi _{2,{\mathrm {\acute {e}t}}\ast }$. The lemma now follows from the Grothendieck spectral sequence.

To prove Theorem 3.6, we now apply the left-exact functor $\underline {\mathrm {Hom}}({\widehat {\mathbb {Z}}},-)$ to (12) and find

\[ \underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}})=\underline{\mathrm{Hom}}({\widehat{\mathbb{Z}}},\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}) \]

by Proposition 3.17, hence

\[ (R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}})^\mathrm{tt}=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}. \]

Since $\mathbb {G}_m^{\mathrm {tt}}$ is strongly topologically torsion by Proposition 2.14, Lemma 2.13 guarantees that the $v$-sheaf $R^1\pi _{{\mathrm {\acute {e}t}}\ast }\mathbb {G}_m^{\mathrm {tt}}$ is topologically torsion, thus the left-hand side equals

\[ (R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}})^\mathrm{tt}=R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}}. \]

This finishes the proof of part (i) of Theorem 3.6.

For the second part, we need to incorporate the character variety into the picture.

3.6 Relation to the character variety

Let $Y$ be an affinoid perfectoid space over $K$. The Cartan–Leray short exact sequence for the $\pi _1(X)$-torsor $\widetilde X\times Y\to X\times Y$ and the sheaf $\mathbb {G}_m$ yields an exact sequence

(15)\begin{equation} 0\to H^1_{{\operatorname{cts}}}(\pi_1(X),\mathbb{G}_m(\widetilde X\times Y))\to \operatorname{Pic}_v(X\times Y)\to \operatorname{Pic}_v(\widetilde X\times Y). \end{equation}

By Proposition 3.9, $\mathbb {G}_m(\widetilde X\times Y)=\mathbb {G}_m(Y)$, so the first term equals $\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X),\mathbb {G}_m(Y))$. Using the character variety from Lemma 3.3, we thus obtain a left-exact sequence on $\operatorname {Perf}_{K,v}$

\[ 0\to\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)\to \mathbf{Pic}_{X,v}\to \mathbf{Pic}_{\widetilde X,v}. \]

We can describe the composition of the first map with $\mathrm {HTlog}$ more explicitly: recall that $\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)=\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}^\mathrm {tt}_m)$, so we can compose characters with $\log :\mathbb {G}_m^\mathrm {tt}\to \mathbb {G}_a$.

Lemma 3.19 The following square is commutative and has a surjective diagonal.

Proof. By functoriality of the Cartan–Leray sequence (left square) and the definition of $\mathrm {HTlog}$ in [Heu21a, Proposition 2.15] (right square), the following diagram commutes.

This shows commutativity. That the left map is surjective follows from Lemma 3.3 and surjectivity of $\log :\mathbb {G}_m^\mathrm {tt}\to \mathbb {G}_a$. The map $\mathrm {HT}$ is surjective by [Heu21a, Proposition 2.6].

We can now put everything together: the diagram from Lemma 3.19 combines with (15) and the sequences from Theorems 3.5 and 3.6(i) to a commutative diagram

with left-exact rows. By Corollary 3.12, the morphism in the rightmost column is injective. By Lemma 3.19, the bottom dashed diagonal map is surjective. It follows from a diagram chase that $\mathbf {Pic}_{X,v}\to \mathbf {Pic}_{\widetilde X,v}$ admits a factorisation through the top dashed arrow: for example, it suffices to observe that by the snake lemma, the cokernels of the two horizontal maps in the top left square are isomorphic. Applying $\operatorname {Hom}({\widehat {\mathbb {Z}}},-)$, we deduce from Proposition 3.17 that this map becomes trivial, and we can thus argue as in the first part to deduce from the middle exact sequence that

\[ \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)= \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)^\mathrm{tt}=\mathbf{Pic}_{X,v}^\mathrm{tt}, \]

where the first equality follows from Lemma 3.3. This finishes the proof of Theorem 3.6(ii).

4. The morphism of Deninger and Werner

We now use Theorem 3.6 to give a reinterpretation, a generalisation, and a geometrisation of a construction of Deninger and Werner in the context of the $p$-adic Simpson correspondence.

Let $X$ be a connected smooth projective curve over $\overline {\mathbb {Q}}_p$. We fix a base-point $x\in X(\overline {\mathbb {Q}}_p)$. In [DW05b], Deninger and Werner construct a functor from a certain category of vector bundles on $X_{\mathbb {C}_p}$ to $\mathbb {C}_p$-linear representations of the étale fundamental group $\pi _1(X):=\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$ of $X$, thus defining a $p$-adic Simpson functor in the case of vanishing Higgs field, or in other words a partial analogue of Narasimhan–Seshadri theory. In [DW05a], they go on to study this functor in the case of line bundles under the additional assumption that $X$ has good reduction: in this case, their functor induces an injective continuous homomorphism

\[ \alpha:\mathbf{Pic}^{0}_X(\mathbb{C}_p)\to \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1(X),\mathbb{C}_p^\times)=\operatorname{Hom}_{{\operatorname{cts}}}(TA^\vee,\mathbb{C}_p^\times), \]

where $A=\mathbf {Pic}^{0}_X(\mathbb {C}_p)$ is the Jacobian of $X$ and $TA^\vee$ is the adelic Tate module of its dual, i.e. of the Albanese. Deninger and Werner give an explicit description of $\alpha$ in terms of the Weil pairing of $A$, and extend their construction to any connected smooth proper algebraic variety $X$ over $\overline {\mathbb {Q}}_p$ satisfying a certain good reduction assumption (see [DW05b, § 1.5]), obtaining more generally a morphism $\alpha$ defined on the $\mathbb {C}_p$-points of the open and closed subgroup $\mathbf {Pic}^{\tau }_X$ of the Picard variety whose image in the Néron–Severi group is torsion.

In the case that $X$ is a curve over $\overline {\mathbb {Q}}_p$ with good reduction, Song [Son22] has recently shown that the morphism $\alpha$ can be ‘geometrised’, i.e. interpreted as the $\mathbb {C}_p$-points of a morphism of rigid group varieties.

4.1 Geometrisation of Deninger and Werner's morphism

We now generalise and geometrise the results of Deninger and Werner and Song to any smooth proper rigid space $X$ of arbitrary dimension over any complete algebraically closed field $K$ over $\mathbb {Q}_p$. For this we use a completely different method based on Theorems 3.5 and 3.6. Namely, we have the following result, which includes a topologically torsion version of Theorem 3.5.

Theorem 4.1 Let $X$ be a connected smooth proper rigid space over $K$. Then we have the following.

1. (i) The topologically torsion Picard functor

   \[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}=R^1\pi_{{\mathrm{\acute{e}t}}\ast}\mathbb{G}_m^{\mathrm{tt}} \]
   is represented by a disjoint union of rigid analytic divisible groups.

2. (ii) There is a natural short exact sequence of rigid group varieties

   (16)\begin{equation} 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\to \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)\xrightarrow{\mathrm{HTlog}} \mathcal{A}\to 0, \end{equation}
   where $\mathcal {A}:=H^0(X,\Omega ^1_X(-1))\otimes \mathbb {G}_a$. It is functorial in $X\to \operatorname {Spa}(K)$ and canonically isomorphic to the topologically torsion part of the sequence (11) in Theorem 3.5.

3. (iii) The exact sequence obtained from (16) by passing to Lie algebras, i.e. tangent spaces at the identity, is canonically identified with the Hodge–Tate sequence

   \[ 0\to H^1_{\mathrm{an}}(X,\mathcal{O})\to H^1_{{\mathrm{\acute{e}t}}}(X,\mathbb{Q}_p)\otimes_{\mathbb{Q}_p} K\xrightarrow{\mathrm{HT}} H^0(X,\Omega^1(-1))\to 0. \]

4. (iv) The first map of (16) induces a natural non-degenerate pairing of adic groups

   \[ \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \underline{\pi_1(X)}\to \mathbb{G}_m. \]

5. (v) If $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\tau }$ is an abeloid variety, then the pairing in part (iv) is the unique analytic continuation of the Weil pairing.

The first morphism in (16) generalises the map $\alpha$ of Deninger and Werner and Song. Indeed, if $\mathbf {Pic}^{\tau }_{X,{\mathrm {\acute {e}t}}}$ is abeloid and $K=\mathbb {C}_p$, then by Proposition 2.23, we have $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}(\mathbb {C}_p)=\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}(\mathbb {C}_p)$.

However, this is no longer true over more general fields, where we need to use the topologically torsion subsheaf rather than all of $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\tau$ to define $\alpha$. The last part is our analogue of the statement in [DW05a, § 4] that $\alpha$ is an extension of the Weil pairing in the case of curves.

Remark 4.2 We note that in contrast to [Son22, Theorem 1.0.1], the domain of our morphism is not $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ but the open subspace $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\subseteq \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$. For curves over $\mathbb {C}_p$, both spaces have the same $\mathbb {C}_p$-points, but the latter has more points when considered as an adic space. In particular, the assumptions of [Son22, Theorems 1.0.1 and 1.0.3] are never satisfied. Indeed, note that any morphism from the proper space $\mathbf {Pic}^0_{X,{\mathrm {\acute {e}t}}}$ to $\mathbb {G}_m$ is trivial. That said, for curves, one can use Song's construction to explicitly define a map on $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$.

Remark 4.3 As pointed out in Remark 1.5, in the setting of curves, the analogue of the short exact sequence of Theorem 4.1 in the complex analytic setting of the Corlette–Simpson correspondence is only real-analytic. This difference to the $p$-adic case can in part be attributed to the fact that the pro-étale fundamental group appearing in Theorem 4.1 is profinite and thus ignores the second factor in the decomposition $\mathbb {C}_p^\times =\mathcal {O}_{\mathbb {C}_p}^\times \times \mathbb {Q}$.

Proof of Theorem 4.1 We first construct the exact sequence (16) in $v$-sheaves: as such, it arises from (11) by applying the functor $-^\mathrm {tt}$ from § 2.2. To see that this preserves exactness, we use that by [Heu21a, Theorem 2.7.3], the sequence (11) is split over the open subgroup

\[ \mathcal{A}^+\subseteq \mathcal{A}:=H^0(X,\Omega^1)(-1)\otimes_K \mathbb{G}_a \]

defined by the image of $\underline {\mathrm {Hom}}(\pi _1(X),p\mathbb {G}_a^+)$ under the morphism $\mathrm {HT}:\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_a)\to \mathcal {A}$. More explicitly, let $\mathbf {Pic}_{X,v}^+$ be the pullback under $\mathrm {HTlog}$ of $\mathcal {A}^+$, then the induced sequence

\[ 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\to \mathbf{Pic}_{X,v}^+\to \mathcal{A}^+\to 0 \]

is split and, in particular, exactness is preserved by the additive functor $-^{\mathrm {tt}}$. This shows left-exactness. Right-exactness follows from Lemma 3.19.

We deduce that $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$ is the kernel of a morphism of rigid groups. Hence, it is itself representable by a rigid group. Since the other terms in (16) are disjoint unions of analytic divisible groups, so is $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$. We have thus shown parts (i) and (ii).

In order to deduce part (iii), we note that adding kernels to Lemma 3.19 induces the following morphism of short exact sequences.

Since the middle arrow is an isomorphism in a neighbourhood of the identity (because $\log$ is), this induces an isomorphism between the associated sequences on tangent spaces.

The pairing in part (iv) is associated to the map $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ by the adjunction of $\otimes$ and $\underline {\mathrm {Hom}}$. It remains to prove part (v). Via the theory of the rigid Albanese variety developed in [HL20, § 4], and using the functoriality of Theorem 3.5, we can reduce to the case that $X$ is itself an abeloid variety. We postpone the explicit description of the pairing in the abeloid case to the next subsection.

First, we give two corollaries. For this we first note the following very general fact.

Remark 4.4 Given any short exact sequence of rigid groups $0\to A\to B\xrightarrow {q} C\to 0$ (say, in the étale topology), we can forget the group structure on $B$ and $C$ and regard the map $q:B\to C$ as an $A$-torsor in a natural way. (Slightly more precisely, it is a torsor in $C_{\mathrm {\acute {e}t}}$ under the group object in $C_{\mathrm {\acute {e}t}}$ represented by $A\times C\to C$, but we still call this an $A$-torsor.) Indeed, over any étale cover $D\to C$ where $q$ admits a splitting $s:D\to B$ over $C$, the natural map $A\times D\to B\times _CD$ is an isomorphism with inverse $(b,d)\mapsto (b-s(d),d)$.

With Remark 4.4 in mind, we can deduce the following from combining Theorems 3.5 and 4.1.

Corollary 4.5

1. (i) The map $\mathrm {HTlog}:\mathbf {Pic}_{X,v}\to \mathcal {A}$ is an étale $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$-torsor.

2. (ii) The map $\mathrm {HTlog}:\underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)\to \mathcal {A}$ is an étale $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$-torsor.

3. (iii) The torsor in part (i) is the pushout of the torsor in part (ii) along $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$.

Corollary 4.6 The sequences (11) and (16) are never split unless $H^0(X,\Omega _X^1)=0$. Indeed, any morphism $\mathcal {A}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ is constant.

Proof. Any splitting of (16) would be a morphism of rigid spaces $s:\mathcal {A}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$. While its source is a product of copies of $\mathbb {G}_a$, each connected component of the target is contained in an affinoid subspace of $\mathbb {G}_m^d$ for some $d\in \mathbb {N}$. Hence, $s$ is constant.

The statement for (11) follows as we obtain (16) from (11) by applying the functor $-^\mathrm {tt}$.

4.2 The Weil pairing from a pro-étale perspective

We now prove Theorem 4.1(v), namely that the pairing from part (iv) can be described as a unique analytic continuation of the Weil pairing if $X$ is abeloid. This is a pleasant application of Theorem 3.6 in its own right.

Remark 4.7 We note that it has long been known that such analytic Weil pairings exists: for abelian varieties of good reduction this is constructed in [Tat67, § 4]. Another related construction is by Fontaine [Fon03, Proposition 1.1] who gives for any abelian variety $A$ over a finite extension $L$ of $\mathbb {Q}_p$ a natural continuous Galois-equivariant homomorphism that reinterpreted in our notation (via Propositions 2.23 and 2.14) is of the form

\[ A\langle p^\infty\rangle(\overline L)\to T_pA(-1)\otimes (1+\mathfrak m_{\mathbb{C}_p})=\underline{\mathrm{Hom}}(T_pA^\vee,\mathbb{G}_m). \]

By comparing Fontaine's construction to ours, it is clear that (the topologically $p$-torsion part of) the analytic Weil pairing from Theorem 4.1 is a geometrisation of Fontaine's map.

Let $A$ be an abeloid variety over $K$. The Weil pairing of $A$ is the perfect pairing

\[ \mathbf{e}_N:A[N]\times A^\vee[N]\to \mu_{N} \]

defined as follows: let $\mathcal {P}$ be the Poincaré bundle on $A\times A^\vee$, then by bilinearity its restriction to $A\times A^\vee [N]$ has trivial $N$th tensor power. It follows that $\mathcal {P}$ admits a canonical reduction of structure group to a $\mu _N$-torsor $\mathcal {P}_N$ on $A\times A^\vee$ that becomes trivial after pullback along $[N]:A\to A$. Consequently, we have a natural commutative diagram of bi-extensions

(17)

and the Weil pairing is defined as the induced arrow on the left.

We can now extend this construction using the universal cover $\widetilde A$ of $A$ from § 3.3. In the abeloid case, this is given by the space $\widetilde A=\textstyle \varprojlim _{[N],N\in \mathbb {N}}A$ and thus sits in an exact sequence

\[ 0\to TA\to \widetilde A\to A\to 0, \]

where $TA=\pi ^{\mathrm {\acute {e}t}}_1(A,0)=\varprojlim _{N\in \mathbb {N}} A[N]$ is the Tate module of $A$. We now restrict to the open subspace $A\times A^{\vee \mathrm {tt}}\subseteq A\times A^\vee$. By Theorem 3.6(i), this is the locus where $\mathcal {P}$ admits a reduction of structure group to a $\mathbb {G}_m^{\mathrm {tt}}$-torsor $\widehat {\mathcal {P}}$, which inherits from $\mathcal {P}$ the structure of a bi-extension

\[ 1\to \mathbb{G}_m^\mathrm{tt}\to \widehat{\mathcal{P}}\to A\times A^{\vee\mathrm{tt}}\to 0. \]

Concretely, this means that it becomes an exact sequence of abelian sheaves on $\mathrm {LSD}_{A}$ and $\mathrm {LSD}_{A^{\vee \mathrm {tt}}}$, respectively, when restricted to test objects relatively over either factor.

By Theorem 3.6(i), this bi-extension becomes trivial upon pullback to $\widetilde A$. Using the short exact sequence of $\widetilde A$, we thus obtain a pushout diagram of adic groups relatively over $A^{\vee \mathrm {tt}}$

where the middle arrow exists because $\mathcal {P}$ becomes split on $\widetilde A\times A^{\vee \mathrm {tt}}$, and is unique because any two morphisms differ by a map from $\widetilde A$ to $\mathbb {G}_m^\mathrm {tt}$, which has to be trivial by Proposition 3.9.

On the left, we thus obtain the desired bilinear pairing $\mathbf {e}:TA\times A^{\vee \mathrm {tt}}\to \mathbb {G}^\mathrm {tt}_m$. It is clear from the construction via pullback to $\widetilde A$ that this is precisely the pairing from Theorem 4.1. On the other hand, it is also clear from comparing to the pullback of (17) to $\widetilde A$ that this gives an analytic continuation of the adelic Weil pairing

\[ (\mathbf{e}_N)_{N\in\mathbb{N}}:TA\times \textstyle\varinjlim_{N\in\mathbb{N}}A^\vee[N]\to \mu. \]

It remains to see that this property determines $\mathbf {e}$ uniquely: for this we use that by Proposition 2.14, for each $x\in TA$ the morphism $\mathbf {e}(x,-)$ is uniquely determined by its value on prime-to-$p$ torsion and a morphism on the analytic $p$-divisible group $A\langle p^\infty \rangle \to \mathbb {G}_m\langle p^\infty \rangle$. By fully faithfulness of Fargues’ functor from $p$-divisible groups to analytic $p$-divisible groups [Far19, Théorème 6.1], this is uniquely determined on $p$-torsion points, as desired.

Remark 4.8 As an application of Theorem 4.1, we point out that the geometric Simpson correspondence can, in turn, be used to study classical rigid analytic Picard functors.

It is expected that for any smooth proper rigid space $X$, the Picard functor $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is represented by a rigid group, and many instances of this are known, see [Heu21a, § 1]. In all known cases, one additionally has the structural result that the identity component $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^0$ is a semi-abeloid variety, i.e. an extension of an abeloid by a rigid torus, see especially [HL00]. However, it currently seems an open question if one should expect such a description in general.

From this perspective, Theorem 4.1 gives the new result that a topologically torsion variant of the Picard functor is always representable. In particular, if $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ is representable by a rigid group, this describes its open topologically torsion subgroup. From this we can deduce structural results on $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{\mathrm {tt}}$ which provide evidence that $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^0$ might always be representable by a semi-abeloid variety. Namely, Theorem 4.1 imposes concrete structural restrictions on what rigid groups can appear as Picard varieties, such as existence of an analytic Weil pairing on topological torsion, which are consistent with $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^{0}$ being semi-abeloid.

As a basic example, we recover [HL00, Lemma 3.1], which says $\operatorname {Hom}(\mathbb {G}_a,\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}})=0$. Indeed, as $\mathbb {G}_a=\mathbb {G}_a^\mathrm {tt}$, any such map factors through $\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}\hookrightarrow \operatorname {Hom}(\pi _1(X),\mathbb {G}_m)$, but $\operatorname {Hom}(\mathbb {G}_a,\mathbb {G}_m)=0$. Similarly, if $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ was an open unit ball with additive structure, this would contradict it being the kernel of a map from $\operatorname {Hom}(\pi _1(X),\mathbb {G}_m)$ to an affine group.

5. Comparison of analytic moduli spaces

In this final section, we use our main theorems to show that the $p$-adic Simpson correspondence in rank one admits a geometric description in terms of a comparison of moduli spaces. This also proves Theorem 1.1 and explains the necessary choices in a geometric way.

As before, let $X$ be a connected smooth proper rigid space $X$ over an algebraically closed complete extension $K$ of $\mathbb {Q}_p$ and choose a base-point $x\in X(K)$ to define $\pi _1(X):=\pi _1^{{\mathrm {\acute {e}t}}}(X,x)$. For simplicity, let us assume in this section that the classical rigid analytic Picard functor is representable (see Remark 4.8). As an application of Theorems 3.6 and 4.1, we can now define rigid analytic moduli spaces on both sides of the $p$-adic Simpson correspondence, in very close analogy to Simpson's complex analytic moduli spaces of rank one [Sim93, § 2].

Definition 5.1

1. (i) The coarse moduli space of $v$-line bundles on $X$ is

   \[ \mathbf{Bun}_{v,1}:=\mathbf{Pic}_{X,v}. \]

2. (ii) Write $\mathcal {A}:=H^0(X,\Omega ^1(-1))\otimes \mathbb {G}_a$, this is the Hitchin base of rank one. Then

   \[ \mathbf{Higgs}_1:=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}\times \mathcal{A} \]
   is the coarse moduli space of Higgs line bundles on $X$.

3. (iii) We define the Betti moduli space to be the character variety of Lemma 3.3,

   \[ \mathbf{M}_{\mathrm{B}}:=\underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_m)=\mathbf{Pic}_{X,v}^{\mathrm{tt}}\subseteq \mathbf{Pic}_v, \]
   which is the moduli space of characters of $\pi _1(X)$. Via Theorem 3.6(ii), we can equivalently see this as the coarse moduli space of topologically torsion $v$-line bundles.

4. (iv) We define the Dolbeault moduli space to be the coarse moduli space

   \[ \mathbf{M}_{\mathrm{Dol}}:=\mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^{\mathrm{tt}}\times \mathcal{A} \subseteq \mathbf{Higgs}_1 \]
   of topologically torsion Higgs line bundles on $X$.

While a priori defined as $v$-sheaves on $\operatorname {Perf}_K$, Theorems 3.5, 4.1 and Lemma 3.3 combine to show that all of the above moduli functors are represented by smooth rigid spaces. This allows us to investigate a new perspective on the $p$-adic Simpson correspondence, namely whether it admits a description in terms of moduli spaces.

This turns out to be the case: in this section, we note three slightly different ways in which we can compare $\mathbf {Bun}_{v,1}$ to $\mathbf {Higgs}_1$, respectively $\mathbf {M}_{\mathrm {B}}$ to $\mathbf {M}_{\mathrm {Dol}}$. The basic idea for this comparison is that $\mathrm {HTlog}$ on the Betti side, and the projection to $\mathcal {A}$ on the Dolbeault side, define a diagram

in which by Corollary 4.5, the second column consists of $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$-torsors, and the first column consists of $\mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$-torsors. While the torsors on the bottom line are split, the torsors on the top line are typically not split according to Corollary 4.6. The first, rather primitive way in which the two sides can be compared is now the following ‘tautological comparison’, based on the observation that any extension becomes tautologically split after pullback to itself.

Corollary 5.2 There is a canonical and functorial isomorphism of rigid groups

\[ \mathbf{Bun}_{v,1}\times_{\mathcal{A}}\mathbf{Bun}_{v,1}{\tilde{\to}} \mathbf{Higgs}_1\times_{\mathcal{A}}\mathbf{Bun}_{v,1}, \]

given by $(L_1,L_2)\mapsto ((L_1\otimes L_2^{-1},\mathrm {HTlog}(L_1)),L_2)$. It restricts to an isomorphism of rigid groups

\[ \mathbf{M}_{\mathrm{B}} \times_{\mathcal{A}} \mathbf{M}_{\mathrm{B}} {\tilde{\to}} \mathbf{M}_{\mathrm{Dol}} \times_{\mathcal{A}} \mathbf{M}_{\mathrm{Dol}}. \]

Our second comparison isomorphism is geometrically more refined but no longer completely canonical: it relies on the observation that the exact sequence (16) in Theorem 4.1 admits a reduction of structure groups to the $p$-torsion subsheaf $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\subseteq \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$.

Definition 5.3 Let $\mathbb {X}$ be any flat $B_{\mathrm {dR}}^+/\xi ^2$-lift of $X$, which by Remark 1.4 induces a splitting $s_{\mathbb {X}}$ of the Hodge–Tate sequence (2). Then we define the étale sheaf $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ as the pullback

where $\widehat {\mathbb {G}}_m:=\mathbb {G}_m\langle p^\infty \rangle$ is the open disc of radius $1$ around $1$, and the bottom row is obtained by applying $\underline {\mathrm {Hom}}(\pi _1(X),-)$ to the logarithm sequence $0\to \mu _{p^\infty }\to \widehat {\mathbb {G}}_m\xrightarrow {\log } \mathbb {G}_a\to 0$.

The sheaf $\mathbb {L}_{\mathbb {X}}$ induces the following ‘étale comparison isomorphism’.

Theorem 5.4 There is a canonical isomorphism

\[ \mathbf{Bun}_{v,1}\times_{\mathcal{A}}\mathbb{L}_{\mathbb{X}}{\tilde{\to}} \mathbf{Higgs}_{1}\times_{\mathcal{A}}\mathbb{L}_{\mathbb{X}}. \]

It restrict to an isomorphism

\[ \mathbf{M}_{\mathrm{B}}\times_{\mathcal{A}}\mathbb{L}_{\mathbb{X}}{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}\times_{\mathcal{A}}\mathbb{L}_{\mathbb{X}}. \]

Proof. The defining sequence of $\mathbb {L}_{\mathbb {X}}$ is a reduction of structure group of the short exact sequence from Theorem 4.1: this follows from combining Definition 5.3 with

and the fact that $\mathrm {HT}\circ s_{\mathbb {X}}={\operatorname {id}}$. Since $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ is a $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$ torsor, there is a canonical isomorphism $\mathbb {L}_{\mathbb {X}}\times _{\mathcal {A}}\mathbb {L}_{\mathbb {X}}{\tilde{\to}} {\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]} \times \mathbb {L}_{\mathbb {X}}$, like in Corollary 5.2. Forming the pushout of the $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]$-torsor in the first factor along $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$ gives the second isomorphism. Pushing further along $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}$ gives the first by Corollary 4.5.

Finally, there is an étale version which is completely canonical, and which can be described as a universal version of Theorem 5.4 over the moduli space of all Hodge–Tate splittings.

Definition 5.5 Let $\mathcal {S}$ be the rigid affine space associated to the finite $K$-vector space

\[ \operatorname{Hom}_K(H^0(X,\Omega^1_X(-1)),\operatorname{Hom}_{{\operatorname{cts}}}(\pi_1(X),K)). \]

Set $\mathcal {A}_{\mathcal {S}}:=\mathcal {A}\times \mathcal {S}$. Then there is a tautological morphism

\[ s:\mathcal{A}_{\mathcal{S}}\to \underline{\mathrm{Hom}}(\pi_1(X),\mathbb{G}_a). \]

We use it to define a universal étale sheaf $\mathbb {L}\to \mathcal {A}_{\mathcal {S}}$ via the following commutative diagram.

Then for any lift $\mathbb {X}$ of $X$ corresponding to a point $x\in \mathcal {S}(K)$, the fibre of $\mathbb {L}$ over $\mathcal {A}\times x$ is $\mathbb {L}_{\mathbb {X}}$.

We let $\mathcal {P}$ be the pushout of $\mathbb {L}$ along $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}^\mathrm {tt}$. This is an extension

\[ 0\to \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}^\mathrm{tt}\to \mathcal{P}\to \mathcal{A}_{\mathcal{S}}\to 0. \]

Note that this is completely canonical and does not depend on either lifts or exponentials.

We now have the following ‘universal comparison isomorphism’: in a way reminiscent of the Deligne–Hitchin twistor space in complex geometry [Sim97, § 4], this exhibits $\mathbf {M}_{\mathrm {Dol}}$ as a ‘degeneration’ of $\mathbf {M}_{\mathrm {B}}$ in the sense that there is an analytic morphism over a base $\mathcal {S}$ whose fibres are generically isomorphic to $\mathbf {M}_{\mathrm {B}}$, but whose fibre over a special point is equal to $\mathbf {M}_{\mathrm {Dol}}$. (This is not to say that the universal comparison is directly related to $\lambda$-connections over $X$, whose closest known analogue are the $q$-connections of Morrow and Tsuji [MT21, § 2].)

Proposition 5.6

1. (i) For any $B_{\mathrm {dR}}^+/\xi ^2$-lift $\mathbb {X}$ of $X$, there is for the fibre $\mathcal {P}_x$ of $\mathcal {P}$ over the associated point $x\in \mathcal {S}(K)$ a canonical isomorphism

   \[ \mathcal{P}_x{\tilde{\to}} \mathbf{M}_{\mathrm{B}}. \]

2. (ii) For any morphism $x:H^1_{{\mathrm {\acute {e}t}}}(X,\Omega ^1)\to H^1_{{\mathrm {\acute {e}t}}}(X,\mathbb {Q}_p)\otimes K=\operatorname {Hom}_{{\operatorname {cts}}}(\pi _1(X),K)$ factoring through the Hodge–Tate filtration, we instead have a canonical isomorphism

   \[ \mathcal{P}_x{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}. \]

3. (iii) There is a canonical and functorial isomorphism of rigid spaces

   \[ c: \mathcal{P}\times_{\mathcal{A}_{\mathcal{S}}}\mathbb{L}{\tilde{\to}} \mathbf{M}_{\mathrm{Dol}}\times_{\mathcal{A}}\mathbb{L} \]
   such that for any $B_{\mathrm {dR}}^+/\xi ^2$-lift $\mathbb {X}$ of $X$, the fibre of $c$ over the associated point $x\in \mathcal {S}(K)$ is canonically identified via part (i) with the isomorphism from Theorem 5.4.

The analogous statements hold for $\mathbf {Bun}_1$, $\mathbf {Higgs}_{1}$ instead of $\mathbf {M}_{\mathrm {B}}$, $\mathbf {M}_{\mathrm {Dol}}$, respectively.

Proof. We have a commutative diagram

inducing a natural map $\mathcal {P}\to \underline {\mathrm {Hom}}(\pi _1(X),\mathbb {G}_m)$ by the universal property of the pushout.

Part (i) follows from comparing the definition of $\mathbb {L}$ to that of Definition 5.3, since in this case the morphism on the right becomes the identity.

To show part (ii), observe that in this case $\mathrm {HT}\circ s$ specialises to $0$. Thus, there is a canonical morphism $\mathbb {L}_x\to \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$ which induces a canonical splitting of $\mathcal{P}_x$. This is the same datum as an isomorphism $\mathcal {P}_x{\tilde{\to}} \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}\times \mathcal {A}=\mathbf {M}_{\mathrm {Dol}}$.

Finally, part (iii) follows from the tautological splitting

\[ \mathbb{L}\times_{\mathcal{A}_{\mathcal{S}}}\mathbb{L}{\tilde{\to}} \mathbf{Pic}_{X,{\mathrm{\acute{e}t}}}[p^\infty]\times_{\mathcal{A}_S}\mathbb{L} \]

after pushout along $\mathbf {Pic}_{X,{\mathrm {\acute {e}t}}}[p^\infty ]\to \mathbf {Pic}^\mathrm {tt}_{X,{\mathrm {\acute {e}t}}}$. The last part of part (iii) about compatibility with Theorem 5.4 over $x\in \mathcal {S}(K)$ is clear from comparing the proofs.

It remains to note that this explains the choices in Theorem 1.1 in a geometric fashion.

Proof of Theorem 1.1 It is clear from the definition that any choice of exponential induces a continuous splitting $s$ of $\mathbb {L}_{\mathbb {X}}\to \mathcal {A}$ on $K$-points, which induces the desired homeomorphism

\[ \operatorname{Hom}_{{\operatorname{cts}}}(\pi_1(X),K^\times)=\mathbf{M}_{\mathrm{B}}(K){\tilde{\to}}\mathbf{M}_{\mathrm{Dol}}(K)=\operatorname{Pic}^\mathrm{tt}_X(K)\times H^0(X,\Omega^1)(-1) \]

by taking $K$-points in Theorem 5.4 and considering the fibre over $s:\mathcal {A}(K)\to \mathbb {L}_{\mathbb {X}}(K)$.

Remark 5.7 As an aside, Theorem 5.4 means that the term ‘geometric $p$-adic Simpson correspondence’ in the title may be interpreted quite literally: it provides a diagram

which is indeed an ‘étale correspondence’ in the sense of algebraic geometry.

Remark 5.8 The results of this section give an indication for what kind of geometric results one can expect also in higher rank. More precisely, we believe that the statements of Theorem 5.4, Proposition 5.6 and Remark 5.7 stand a chance to generalise: this suggests that the moduli space of $v$-vector bundles is an étale twist of the moduli space of Higgs bundles over the Hitchin base, and that the usual choices necessary for the formulation of the $p$-adic Simpson correspondence can be interpreted as leading to a trivialisation of this twist.

We show in [Heu22c] that indeed, one can construct analytic moduli spaces of $v$-vector bundles and Higgs bundles in terms of small $v$-stacks, and that both admit natural maps to the Hitchin base. This provides further evidence that the results of this article provide the first instance of a general moduli-theoretic approach to the $p$-adic Simpson correspondence.