Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T04:18:26.820Z Has data issue: false hasContentIssue false
  • English
  • Français

The genus-one global mirror theorem for the quintic 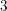$3$-fold

Part of: Symplectic geometry, contact geometry Projective and enumerative geometry

Published online by Cambridge University Press:  30 April 2019

Shuai Guo  and
Dustin Ross
Shuai Guo
Affiliation:
School of Mathematical Sciences, Peking University, No 5, Yiheyuan Road, Beijing 100871, China email [email protected]
Dustin Ross
Affiliation:
Department of Mathematics, San Francisco State University, Thornton Hall 941, 1600 Holloway Avenue, San Francisco, CA 94132, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the genus-one restriction of the all-genus Landau–Ginzburg/Calabi–Yau conjecture of Chiodo and Ruan, stated in terms of the geometric quantization of an explicit symplectomorphism determined by genus-zero invariants. This gives the first evidence supporting the higher-genus Landau–Ginzburg/Calabi–Yau correspondence for the quintic 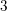$3$-fold, and exhibits the first instance of the ‘genus zero controls higher genus’ principle, in the sense of Givental’s quantization formalism, for non-semisimple cohomological field theories.

Keywords

mirror symmetryGromov–Witten theoryFan–Jarvis–Ruan–Witten theory

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 53D45: Gromov-Witten invariants, quantum cohomology, Frobenius manifolds 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 5 , May 2019 , pp. 995 - 1024
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bershadsky, M., Cecotti, S., Ooguri, H. and Vafa, C., Kodaira–Spencer theory of gravity and exact results for quantum string amplitudes , Comm. Math. Phys. 165 (1994), 311–427.10.1007/BF02099774Google Scholar
Brini, A., Cavalieri, R. and Ross, D., Crepant resolutions and open strings, Preprint (2013),arXiv:1309.4438.Google Scholar
Bertram, A., Another way to enumerate rational curves with torus actions , Invent. Math. 142 (2000), 487–512.10.1007/s002220000094Google Scholar
Candelas, P., de la Ossa, X. C., Green, P. S. and Parkes, L., A pair of Calabi–Yau manifolds as an exactly soluble superconformal theory , Nuclear Phys. B 359 (1991), 21–74.10.1016/0550-3213(91)90292-6Google Scholar
Ciocan-Fontanine, I. and Kim, B., Wall-crossing in genus zero quasimap theory and mirror maps , Algebr. Geom. 1 (2014), 400–448.10.14231/AG-2014-019Google Scholar
Ciocan-Fontanine, I. and Kim, B., Quasmap wall-crossing and mirror symmetry, Preprint (2016), arXiv:1611.05023.Google Scholar
Coates, T. and Iritani, H., A Fock sheaf for Givental quantization , Kyoto J. Math. 58 (2018), 695–864.10.1215/21562261-2017-0036Google Scholar
Coates, T. H., Riemann–Roch theorems in Gromov–Witten theory, PhD thesis, University of California, Berkeley (ProQuest LLC, Ann Arbor, MI, 2003).Google Scholar
Clader, E., Priddis, N. and Shoemaker, M., Geometric quantization with applications to Gromov–Witten theory, Preprint (2013), arXiv:1309.1150.Google Scholar
Chiodo, A. and Ruan, Y., Landau–Ginzburg/Calabi–Yau correspondence for quintic three-folds via symplectic transformations , Invent. Math. 182 (2010), 117–165.10.1007/s00222-010-0260-0Google Scholar
Coates, T. and Ruan, Y., Quantum cohomology and crepant resolutions: a conjecture , Ann. Inst. Fourier (Grenoble) 63 (2013), 431–478.10.5802/aif.2766Google Scholar
Fan, H., Jarvis, T. and Ruan, Y., The Witten equation, mirror symmetry, and quantum singularity theory , Ann. of Math. (2) 178 (2013), 1–106.10.4007/annals.2013.178.1.1Google Scholar
Givental, A., A mirror theorem for toric complete intersections , Progr. Math. 160 (1998), 141–176.Google Scholar
Givental, A., Gromov–Witten invariants and quantization of quadratic Hamiltonians , Mosc. Math. J. 1 (2001), 551–568.10.17323/1609-4514-2001-1-4-551-568Google Scholar
Givental, A., Semisimple Frobenius structures at higher genus , Int. Math. Res. Not. IMRN 2001 (2001), 1265–1286.10.1155/S1073792801000605Google Scholar
Givental, A. B., Symplectic geometry of Frobenius structures , in Frobenius manifolds, Aspects of Mathematics, vol. E36 (Vieweg, Wiesbaden, 2004), 91–112.10.1007/978-3-322-80236-1_4Google Scholar
Guo, S. and Ross, D., Genus-one mirror symmetry in the Landau–Ginzburg model , Algebr. Geom. 6 (2019), 260–301.Google Scholar
Greene, B., Vafa, C. and Warner, N., Calabi-Yau manifolds and renormalization group flows , Nuclear Phys. B 324 (1989), 371–390.10.1016/0550-3213(89)90471-9Google Scholar
Huang, M.-X., Klemm, A. and Quackenbush, S., Topological string theory on compact Calabi–Yau: Modularity and boundary conditions , in Homological mirror symmetry: new developments and perspectives, Lecture Notes in Physics, vol. 757, eds Schlesinger, K.-G., Kreuzer, M. and Kapustin, A. (Springer, Berlin, 2008), 45–102.Google Scholar
He, W., Li, S., Shen, T. and Webb, R., Landau–Ginzburg mirror symmetry conjecture, Preprint (2015), arXiv:1503.01757.Google Scholar
Iritani, H., Milanov, T., Ruan, Y. and Shen, Y., Gromov–Witten theory of quotient of Fermat Calabi–Yau varieties, Preprint (2016), arXiv:1605.08885.Google Scholar
Kim, B. and Lho, H., Mirror theorem for elliptic quasimap invariants , Geom. Topol. 22 (2018), 1459–1481.10.2140/gt.2018.22.1459Google Scholar
Lian, B. H., Liu, K. and Yau, S.-T., Mirror principle. I , Asian J. Math. 1 (1997), 729–763.10.4310/AJM.1997.v1.n4.a5Google Scholar
Lee, Y.-P. and Pandharipande, R., Frobenius manifolds, Gromov–Witten theory and Virasoro constraints, https://people.math.ethz.ch/∼rahul/ (2004).Google Scholar
Martinec, E., Criticality, catastrophes and compactifications , in Physics and mathematics of strings, eds Brink, L., Friedan, D. and Polyakov, A. M. (World Scientific, Singapore, 1989), 389–433.Google Scholar
Teleman, C., The structure of 2D semi-simple field theories , Invent. Math. 188 (2012), 525–588.10.1007/s00222-011-0352-5Google Scholar
Vafa, C. and Warner, N., Catastrophes and the classification of conformal theories , Phys. Lett. B 218 (1989), 51–58.10.1016/0370-2693(89)90473-5Google Scholar
Zinger, A., The reduced genus 1 Gromov–Witten invariants of Calabi–Yau hypersurfaces , J. Amer. Math. Soc. 22 (2009), 691–737.10.1090/S0894-0347-08-00625-5Google Scholar
Zong, Z., Equivariant Gromov–Witten theory of GKM orbifolds, PhD thesis, Columbia University (ProQuest LLC, Ann Arbor, MI, 2015).Google Scholar
Zagier, D. and Zinger, A., Some properties of hypergeometric series associated with mirror symmetry , in Modular forms and string duality, Fields Institute Communications, vol. 54 (American Mathematical Society, Providence, RI, 2008), 163–177.Google Scholar