Article contents
Generating functions on covering groups
Published online by Cambridge University Press: 20 February 2018
Abstract
In this paper we prove a conjecture relating the Whittaker function of a certain generating function with the Whittaker function of the theta representation 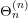 $\unicode[STIX]{x1D6E9}_{n}^{(n)}$. This enables us to establish that a certain global integral is factorizable and hence deduce the meromorphic continuation of the standard partial
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$. This enables us to establish that a certain global integral is factorizable and hence deduce the meromorphic continuation of the standard partial 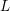 $L$ function
$L$ function 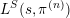 $L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$. In fact we prove that this partial
$L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$. In fact we prove that this partial 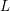 $L$ function has at most a simple pole at
$L$ function has at most a simple pole at 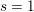 $s=1$. Here,
$s=1$. Here, 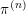 $\unicode[STIX]{x1D70B}^{(n)}$ is a genuine irreducible cuspidal representation of the group
$\unicode[STIX]{x1D70B}^{(n)}$ is a genuine irreducible cuspidal representation of the group 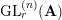 $\text{GL}_{r}^{(n)}(\mathbf{A})$.
$\text{GL}_{r}^{(n)}(\mathbf{A})$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2018
References
- 4
- Cited by


