Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-21T14:43:29.388Z Has data issue: false hasContentIssue false
  • English
  • Français

Floer cohomology of 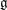$\mathfrak{g}$-equivariant Lagrangian branes

Part of: Lie algebras and Lie superalgebras Symplectic geometry, contact geometry

Published online by Cambridge University Press:  17 December 2015

Yankı Lekili  and
James Pascaleff
Yankı Lekili
Affiliation:
King’s College London, Department of Mathematics, Strand, London WC2R 2LS, UK email [email protected]
James Pascaleff
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, 1409 W. Green St., Urbana, IL 61801, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Building on Seidel and Solomon’s fundamental work [Symplectic cohomology and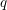$q$-intersection numbers, Geom. Funct. Anal. 22 (2012), 443–477], we define the notion of a 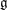$\mathfrak{g}$-equivariant Lagrangian brane in an exact symplectic manifold 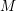$M$, where 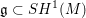$\mathfrak{g}\subset SH^{1}(M)$ is a sub-Lie algebra of the symplectic cohomology of 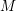$M$. When 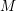$M$ is a (symplectic) mirror to an (algebraic) homogeneous space 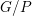$G/P$, homological mirror symmetry predicts that there is an embedding of 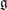$\mathfrak{g}$ in 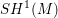$SH^{1}(M)$. This allows us to study a mirror theory to classical constructions of Borel, Weil and Bott. We give explicit computations recovering all finite-dimensional irreducible representations of 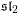$\mathfrak{sl}_{2}$ as representations on the Floer cohomology of an 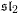$\mathfrak{sl}_{2}$-equivariant Lagrangian brane and discuss generalizations to arbitrary finite-dimensional semisimple Lie algebras.

Keywords

equivariant Lagrangian branessymplectic cohomologyhomological mirror symmetrysemisimple Lie algebras

MSC classification

Primary: 53D40: Floer homology and cohomology, symplectic aspects 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category
Secondary: 17B99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 5 , May 2016 , pp. 1071 - 1110
Copyright
© The Authors 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbondandolo, A. and Schwarz, M., On the Floer homology of cotangent bundles, Comm. Pure Appl. Math. 59 (2006), 254–316; MR 2190223 (2006m:53137).CrossRefGoogle Scholar
Abbondandolo, A. and Schwarz, M., Floer homology of cotangent bundles and the loop product, Geom. Topol. 14 (2010), 1569–1722; MR 2679580 (2011k:53126).Google Scholar
Abouzaid, M., A geometric criterion for generating the Fukaya category, Publ. Math. Inst. Hautes Études Sci. 112 (2010), 191–240; MR 2737980 (2012h:53192).Google Scholar
Abouzaid, M., On the wrapped Fukaya category and based loops, J. Symplectic Geom. 10 (2012), 27–79; MR 2904032.Google Scholar
Abouzaid, M., Symplectic cohomology and Viterbo’s theorem, in Free loop spaces in geometry and topology, IRMA Lectures in Mathematics and Theoretical Physics, vol. 24 (European Mathematical Society, Zürich, 2015), 271–487.Google Scholar
Abouzaid, M. and Seidel, P., An open string analogue of Viterbo functoriality, Geom. Topol. 14 (2010), 627–718; MR 2602848 (2011g:53190).Google Scholar
Auroux, D., Mirror symmetry and T-duality in the complement of an anticanonical divisor, J. Gökova Geom. Topol. GGT 1 (2007), 51–91; MR 2386535 (2009f:53141).Google Scholar
Auroux, D., A beginner’s introduction to Fukaya categories, in Contact and symplectic topology, Bolyai Society Mathematical Studies, vol. 26 (János Bolyai Mathematical Society, Budapest, 2014), 85–136.Google Scholar
Bott, R., Homogeneous vector bundles, Ann. of Math. (2) 66 (1957), 203–248; MR 0089473 (19,681d).CrossRefGoogle Scholar
Chaput, P. E., Manivel, L. and Perrin, N., Quantum cohomology of minuscule homogeneous spaces III. Semi-simplicity and consequences, Canad. J. Math. 62 (2010), 1246–1263; MR 2760657 (2012d:14096).Google Scholar
Eguchi, T., Hori, K. and Xiong, C.-S., Gravitational quantum cohomology, Internat. J. Modern Phys. A 12 (1997), 1743–1782; MR 1439892 (99a:32027).CrossRefGoogle Scholar
Fuks, D. B., Cohomology of infinite-dimensional Lie algebras, Contemporary Soviet Mathematics (Consultants Bureau, New York, 1986), translated from the Russian by A. B. Sosinskiĭ;MR 874337 (88b:17001).Google Scholar
Gepner, D., Fusion rings and geometry, Comm. Math. Phys. 141 (1991), 381–411; MR 1133272 (92j:81271).Google Scholar
Getzler, E., Batalin–Vilkovisky algebras and two-dimensional topological field theories, Comm. Math. Phys. 159 (1994), 265–285; MR 1256989 (95h:81099).CrossRefGoogle Scholar
Givental, A., Stationary phase integrals, quantum Toda lattices, flag manifolds and the mirror conjecture, in Topics in singularity theory, American Mathematical Society Translation Series 2, vol. 180 (American Mathematical Society, Providence, RI, 1997), 103–115; MR 1767115 (2001d:14063).Google Scholar
Goncharov, A. B. and Shen, L., Geometry of canonical bases and mirror symmetry, Invent. Math. 202 (2015), 487–633.CrossRefGoogle Scholar
Kac, V. G. and Raina, A. K., Bombay lectures on highest weight representations of infinite-dimensional Lie algebras, Advanced Series in Mathematical Physics, vol. 2 (World Scientific, Teaneck, NJ, 1987); MR 1021978 (90k:17013).Google Scholar
Kajiura, H. and Stasheff, J., Homotopy algebras inspired by classical open–closed string field theory, Comm. Math. Phys. 263 (2006), 553–581; MR 2211816 (2007g:18004).Google Scholar
Kaplansky, I. and Santharoubane, L. J., Harish-Chandra modules over the Virasoro algebra, in Infinite-dimensional groups with applications (Berkeley, CA, 1984), Mathematical Sciences Research Institute Publications, vol. 4 (Springer, New York, 1985), 217–231; MR 823321 (87d:17013).Google Scholar
Kashiwara, M., On crystal bases of the Q-analogue of universal enveloping algebras, Duke Math. J. 63 (1991), 465–516; MR 1115118 (93b:17045).Google Scholar
Kimura, T., Stasheff, J. and Voronov, A. A., On operad structures of moduli spaces and string theory, Comm. Math. Phys. 171 (1995), 1–25; MR 1341693 (96k:14019).Google Scholar
Knutson, A., Lam, T. and Speyer, D. E., Projections of Richardson varieties, J. Reine Angew. Math. 687 (2014), 133–157.Google Scholar
Kontsevich, M., Homological algebra of mirror symmetry, in Proceedings of the International Congress of Mathematicians, vols. 1, 2 (Zürich, 1994) (Birkhäuser, Basel, 1995), 120–139; MR 1403918 (97f:32040).Google Scholar
Kontsevich, M., Lectures at ENS, Paris, spring 1998, notes taken by J. Bellaiche, J.-F. Dat, I. Marin, G. Racinet and H. Randriambololona, unpublished.Google Scholar
Kostant, B., Flag manifold quantum cohomology, the Toda lattice, and the representation with highest weight 𝜌, Selecta Math. (N.S.) 2 (1996), 43–91; MR 1403352 (97e:17029).Google Scholar
Lusztig, G., Canonical bases arising from quantized enveloping algebras, J. Amer. Math. Soc. 3 (1990), 447–498; MR 1035415 (90m:17023).Google Scholar
Lusztig, G., Quivers, perverse sheaves, and quantized enveloping algebras, J. Amer. Math. Soc. 4 (1991), 365–421; MR 1088333 (91m:17018).CrossRefGoogle Scholar
Mathieu, O., Classification of Harish-Chandra modules over the Virasoro Lie algebra, Invent. Math. 107 (1992), 225–234; MR 1144422 (93d:17034).Google Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166 (2007), 95–143; MR 2342692 (2008m:22027).CrossRefGoogle Scholar
Rietsch, K., A mirror symmetric construction of qH T∗(G/P)(q), Adv. Math. 217 (2008), 2401–2442; MR 2397456 (2009f:14106).CrossRefGoogle Scholar
Ritter, A. F., Topological quantum field theory structure on symplectic cohomology, J. Topol. 6 (2013), 391–489; MR 3065181.Google Scholar
Ritter, A. F. and Smith, I., The monotone wrapped Fukaya category and the open–closed string map, Preprint (2015), arXiv:1201.5880v5.Google Scholar
Salamon, D. A. and Weber, J., Floer homology and the heat flow, Geom. Funct. Anal. 16 (2006), 1050–1138; MR 2276534 (2007k:53154).Google Scholar
Seidel, P., Fukaya categories and deformations, in Proceedings of the International Congress of Mathematicians, vol. II (Beijing, 2002) (Higher Education Press, Beijing, 2002), 351–360; MR 1957046 (2004a:53110).Google Scholar
Seidel, P., A biased view of symplectic cohomology, in Current developments in mathematics, Vol. 2006 (International Press, Somerville, MA, 2008), 211–253; MR 2459307 (2010k:53153).Google Scholar
Seidel, P., Fukaya categories and Picard–Lefschetz theory, Zürich Lectures in Advanced Mathematics (European Mathematical Society, Zürich, 2008); MR 2441780 (2009f:53143).Google Scholar
Seidel, P., Disjoinable Lagrangian spheres and dilations, Invent. Math. 197 (2014), 299–359.Google Scholar
Seidel, P., Lectures on categorical dynamics and symplectic topology, available athttp://math.mit.edu/∼seidel/.Google Scholar
Seidel, P. and Solomon, J. P., Symplectic cohomology and q-intersection numbers, Geom. Funct. Anal. 22 (2012), 443–477; MR 2929070.CrossRefGoogle Scholar
Siebert, B. and Tian, G., On quantum cohomology rings of Fano manifolds and a formula of Vafa and Intriligator, Asian J. Math. 1 (1997), 679–695; MR 1621570 (99d:14060).Google Scholar
Viterbo, C., Functors and computations in Floer cohomology II, Preprint (2003).Google Scholar
Weibel, C. A., An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38 (Cambridge University Press, Cambridge, 1994); MR 1269324 (95f:18001).Google Scholar