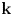Finite orbits for large groups of automorphisms of projective surfaces

Abstract

We study finite orbits of non-elementary groups of automorphisms of compact projective surfaces. We prove that if the surface and the group are defined over a number field $\mathbf {k}$ and the group contains parabolic elements, then the set of finite orbits is not Zariski dense, except in certain very rigid situations, known as Kummer examples. Related results are also established when $\mathbf {k} = \mathbf {C}$. An application is given to the description of ‘canonical vector heights’ associated to such automorphism groups.

1. Introduction

1.1 Setting

Let $X$ be a complex projective surface. Denote by $\mathsf {Aut}(X)$ its group of automorphisms. The action of this group on the Néron–Severi group ${\mathrm {NS}}(X;\mathbf {Z})$ (respectively, on the cohomology group $H^2(X;\mathbf {Z})$) gives a linear representation $f\mapsto f^*$ from $\mathsf {Aut}(X)$ to ${\sf {GL}}({\mathrm {NS}}(X;\mathbf {Z}))$ (respectively, ${\sf {GL}}(H^2(X;\mathbf {Z}))$). By definition, a subgroup $\Gamma$ of $\mathsf {Aut}(X)$ is non-elementary if its image $\Gamma ^*\subset {\sf {GL}}({\mathrm {NS}}(X;\mathbf {Z}))$ (respectively, $\subset {\sf {GL}}(H^2(X;\mathbf {Z}))$) contains a free group of rank $\geq 2$; equivalently, $\Gamma ^*$ does not contain any abelian subgroup of finite index (see [CD23c, CD23a] for details and examples).

Our purpose is to study the existence and abundance of finite (or ‘periodic’) orbits under such non-elementary group actions. Several possible scenarios can be imagined:

1. (a) a large (that is, dense or Zariski dense) set of finite orbits;

2. (b) finitely many finite orbits;

3. (c) no finite orbit at all.

For a cyclic group generated by a single automorphism, the situation is well understood: in many cases the set of periodic points is large (see [Can14] for an introduction to this topic and [Xie15] for the case of birational transformations). On the other hand, for non-elementary groups, we expect the existence of a dense set of periodic points to be a rare phenomenon; this expectation will be confirmed by our results.

The only examples we know for situation (a) are given by abelian surfaces and their siblings, Kummer surfaces. Here, by Kummer surface we mean a smooth surface $X$ which is a (not necessarily minimal) desingularization of the quotient $A/G$ of an abelian surface $A=\mathbf {C}^2/\Lambda$ by a finite group $G\subset \mathsf {Aut}(A)$. If $G$ is generated by the involution $(x,y)\mapsto (-x,-y)$ of $A$, we find the classical Kummer surfaces and their blow-ups (see [BHPV04]). Given a subgroup $\Gamma \subset \mathsf {Aut}(X)$, we say that the pair $(X,\Gamma )$ is a Kummer group if $X$ is a Kummer surface and $\Gamma$ comes from a subgroup of $\mathsf {Aut}(A)$ which normalizes $G$; precise definitions are given in § 5.7. If $\Gamma$ is a group of automorphisms of an abelian surface $A$ fixing the origin $0\in A$, then all torsion points are $\Gamma$-periodic. This implies that most Kummer groups have a dense set of finite orbits (see Proposition 4.5).

1.2 Main results

We first illustrate property (c) in the family of Wehler surfaces, that is for smooth surfaces $X\subset \mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1$ defined by a polynomial equation of degree $(2,2,2)$. Such an $X$ is a K3 surface. Generically, the three projections $X\to \mathbb {P}^1\times \mathbb {P}^1$ are $2$-to-$1$ ramified covers and $\mathsf {Aut}(X)$ is generated by the corresponding involutions. These examples occupy a central position in the dynamical study of surface automorphisms, both from the ergodic and arithmetic points of view (see, e.g., [Sil91, Kaw06, McM02]).

Theorem 1 For a very general Wehler surface $X$, every orbit under $\mathsf {Aut}(X)$ is Zariski dense. In particular there is no finite orbit under the action of $\mathsf {Aut}(X)$.

Unfortunately, the proof of this theorem has an obvious limitation: it does not single out any explicit example defined over $\overline {\mathbf {Q}}$ satisfying property (c).

Our main theorem concerns property (b). To state it, recall that there are three types of automorphisms, characterized by the behavior of the linear endomorphism $f^*$ (see [Can14]). If $f^*$ has finite order, then $f$ is elliptic. It is parabolic if $f^*$ has infinite order, but none of its eigenvalues has modulus ${>}1$; it is loxodromic if some eigenvalue $\lambda (f)$ of $f^*$ has modulus $\vert \lambda (f)\vert >1$ (in that case $\lambda (f)$ is unique and $\lambda (f)\in (1,+\infty )$). A non-elementary group of automorphisms contains a non-abelian free group all of whose non-trivial elements are loxodromic, and a group containing both loxodromic and parabolic elements is automatically non-elementary.

Theorem 2 Let $X$ be a smooth projective surface, defined over some number field ${\mathbf {k}}$. Let $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$, also defined over ${\mathbf {k}}$, containing both parabolic and loxodromic automorphisms. If the set of finite orbits of $\Gamma$ is Zariski dense in $X$, then $(X,\Gamma )$ is a Kummer group.

In the setting of the theorem, and more generally when $\Gamma$ is any group of automorphisms of a complex projective surface $X$ containing a loxodromic element, there is a maximal $\Gamma$-invariant curve $D_\Gamma$; more precisely, either $\Gamma$ does not preserve any curve, or there exists a unique, maximal, $\Gamma$-invariant, Zariski-closed subset of pure dimension $1$. This curve $D_\Gamma$ can be contracted to yield a (singular) complex analytic surface $X_0$ and a $\Gamma$-equivariant birational morphism

(1.1)\begin{equation} \pi_0\colon X\to X_0. \end{equation}

Moreover, when $\Gamma$ contains a parabolic automorphism, $X_0$ is projective (see Proposition 3.9). Another important result towards Theorem B states that any non-elementary subgroup $\Gamma \subset \mathsf {Aut}(X)$ contains a loxodromic element whose maximal invariant curve is equal to $D_\Gamma$ (see Theorem D in § 3). With this notation, Theorem B says that property (b) holds on $X_0$ if $(X,\Gamma )$ is defined over a number field and is not a Kummer group.

Let us stress that even if $X$ and $\Gamma$ are defined over ${\mathbf {k}}$, Theorem B deals with orbits of $\Gamma$ in $X(\mathbf {C})$. This is different from the results of [Sil91, Kaw08], in which a finiteness theorem is obtained for periodic orbits of loxodromic automorphisms in $X({\mathbf {k}}')$, where ${\mathbf {k}}'$ is some fixed number field containing ${\mathbf {k}}$ (it ultimately relies on Northcott's finiteness theorem).

Under the assumptions of Theorem B, we obtain the following corollaries (see Corollaries 6.1, and 6.2 and Proposition 4.5 for details).

• – If $\Gamma$ does not preserve any algebraic curve and $X$ is not an abelian surface, then $\Gamma$ admits at most finitely many finite orbits.

• – If $C$ is an irreducible curve containing infinitely many $\Gamma$-periodic points, then either $C$ is $\Gamma$-periodic or $(X, \Gamma )$ is a Kummer group and $C$ comes from a translate of an abelian subvariety. If $C$ has genus ${\geq }2$, it contains at most finitely many $\Gamma$-periodic points.

• – If $\Gamma$ has a Zariski-dense set of finite orbits, then its finite orbits are dense in $X(\mathbf {C})$ for the Euclidean topology; furthermore, if $f_1$ and $f_2$ are two loxodromic automorphisms in $\Gamma$, their periodic points coincide, except for at most finitely many of them which are located on $\Gamma$-invariant curves.

As we shall see in Remark 6.6, the last statement provides a partial answer to a question of Kawaguchi.

1.3 Proof strategy and extension to complex coefficients

Let us say a few words about the proof of Theorem B (a more detailed outline is given in § 5.1). Given two ‘typical’ loxodromic elements $f,g$ in $\Gamma$, intuition suggests that $\mathrm {Per}(f)\cap \mathrm {Per}(g)$ cannot be Zariski dense unless some ‘special’ phenomenon happens. This situation has been referred to as an unlikely intersection problem in the algebraic dynamics literature (see, e.g., [Zan12, § 3.4]). Previous work on this topic suggests to handle this problem using methods from arithmetic geometry (see, e.g., [BD11, DF17]). In this respect a key idea would be to use arithmetic equidistribution (see [Yua08, BB10]) to derive an equality $\mu _f=\mu _g$ between the measures of maximal entropy of $f$ and $g$. Unfortunately we do not know how to infer rigidity results directly from this equality, so the proof of Theorem B is not based on this sole argument. To reach a conclusion, we make use of the dynamics of the whole group $\Gamma$, in particular of the classification of $\Gamma$-invariant measures (see [Can01b, CD23b]), together with the classification of loxodromic automorphisms $f$ whose measure of maximal entropy $\mu _f$ is absolutely continuous with respect to the Lebesgue measure (see [CD20, FT21]). The existence of parabolic elements in $\Gamma$ is required at three important stages, including the arithmetic step; in particular, we are not able to prove Theorem B without assuming that $\Gamma$ contains parabolic elements (see § 6.3 for a more precise discussion).

Even if arithmetic methods lie at the core of the proof of Theorem B, it is natural to expect that the assumption that $X$ and $\Gamma$ be defined over a number field is superfluous. We are indeed able to get rid of it when $\Gamma$ has no invariant curve.

Theorem 3 Let $X$ be a compact Kähler surface which is not a torus. Let $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$ which contains a parabolic element and does not preserve any algebraic curve. Then $\Gamma$ admits only finitely many periodic points.

The proof of Theorem C is based on specialization arguments, inspired notably by the approach of [DF17] (see § 7). It applies, for instance, to the action of $\Gamma =\mathsf {Aut}(X)$ on any unnodal Enriques surface $X$, and to the foldings of euclidean pentagons with generic side lengths (see [CD23a] for details on these examples).

1.4 Canonical vector heights

Theorem B will be applied to answer a question of Baragar on the existence of certain canonical heights (see [Bar04, BvL07, Kaw13]).

Let $X$ be a projective surface, defined over a number field ${\mathbf {k}}$. Denote by ${\mathrm {Pic}}(X)$ the Picard group of $X_{\overline {\mathbf {Q}}}$. The Weil height machine provides, for every line bundle $L$ on $X$, a height function $h_L\colon X({\overline {\mathbf {Q}}})\to \mathbf {R}$, defined up to a bounded error $O(1)$. This construction is additive, $h_{aL+bL'}=ah_L+bh_{L'}+O(1)$ for all pairs $(L,L')\in {\mathrm {Pic}}(X )^2$ and all coefficients $(a,b)\in \mathbf {Z}^2$. When $L={\mathcal {O}}_X(1)$ for some embedding $X\subset \mathbb {P}^N_{\mathbf {k}}$, then $h_L$ coincides with the usual logarithmic Weil height.

If $f$ is a regular endomorphism of $X$ defined over ${\mathbf {k}}$ and $L$ is an ample line bundle such that $f^*L=L^{\otimes d}$ for some integer $d>1$, then $h_L\circ f = dh_L+O(1)$. Tate's renormalization trick

(1.2)\begin{equation} \hat{h}_L(x):=\lim_{n\to +\infty} \frac{1}{d^n} h_L(f^n(x)) \end{equation}

provides a canonical height for $f$ and $L$, that is, a function $\hat {h}_L\colon X({\overline {\mathbf {Q}}})\to \mathbf {R}_+$ such that $\hat {h}_L=h_L+O(1)$ and $\hat {h}_L\circ f= d\hat {h}_L$ exactly, with no error term. This construction was extended to loxodromic automorphisms of surfaces by Silverman, Call, and Kawaguchi (see [Sil91, CS93, Kaw08]): in this case one obtains a pair of canonical heights $\hat h_f^\pm$ satisfying $\hat h_f^\pm \circ f^{\pm 1} = \lambda (f)^\pm \hat h_f^\pm$. (Here $\hat h_f^+$ and $\hat h_f^-$ are Weil heights associated to $\mathbf {R}$-divisors.)

If $\Gamma$ is an infinite subgroup of $\mathsf {Aut}(X)$, also defined over ${\mathbf {k}}$, it is natural to ask whether a $\Gamma$-equivariant family of heights can be constructed. Specifically, one looks for a family of representatives $\hat {h}_L$ of the Weil height functions, i.e. $\hat {h}_L=h_L+O(1)$ for every $L$ in ${\mathrm {Pic}}(X;\mathbf {R}):={\mathrm {Pic}}(X)\otimes _\mathbf {Z}\mathbf {R}$, depending linearly on $L$, and satisfying the exact relation

(1.3)\begin{equation} \hat{h}_L(f(x))=\hat{h}_{f^*L}(x)\quad (\forall x\in X(\overline{\mathbf{Q}})) \end{equation}

for every pair $(f,L)\in \Gamma \times {\mathrm {Pic}}(X;\mathbf {R})$ (see § 8 for details). A prototypical example is given by the Néron–Tate height, when $\Gamma$ is the group of automorphisms of an abelian surface preserving the origin. Such objects were named canonical vector heights ¹ by Baragar in [Bar03]. He proved their existence when $X$ is a K3 surface with Picard number $2$, in which case $\mathsf {Aut}(X)$ is virtually cyclic. He also gave evidence for their non-existence on certain Wehler surfaces (see [BvL07]). In [Kaw13] Kawaguchi obtained a complete proof of this non-existence for an explicit family of Wehler surfaces; his argument relies on the study of $\Gamma$-periodic orbits. Extending Kawaguchi's methods and using Theorem B, we completely solve this existence problem for groups with parabolic elements: let $X$ be a smooth projective surface and $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(X)$ containing parabolic elements, both defined over a number field ${\mathbf {k}}$; if $(X,\Gamma )$ possesses a canonical vector height, then $X$ is an abelian surface and $\Gamma$ has a finite orbit (see Theorem E in § 8). The last assertion implies that, after conjugation by a translation, a finite index subgroup of $\Gamma$ preserves the neutral element of the abelian surface $X$, in particular the Néron–Tate height provides a canonical vector height; we explain how all possible canonical vector heights are derived from the Néron–Tate height (see § 8.4).

1.5 Stationary measures

Another application, which was our primary source of motivation for this paper, concerns the classification of invariant and stationary measures. For simplicity, we suppose in this section, as in Theorem C, that $X$ is not abelian, $\Gamma$ contains both loxodromic and parabolic elements, and $\Gamma$ does not preserve any algebraic curve.

With the classification and finiteness theorems for invariant Zariski-diffuse measures obtained in [CD23b], Theorem C implies that the set of $\Gamma$-invariant probability measures is a finite dimensional simplex, whose extremal points are given by:

• – uniform counting measures on the finite orbits of $\Gamma$;

• – measures $\mu$ for which there is a $\Gamma$-invariant totally real (possibly singular) surface $\Sigma$ such that $\operatorname {Supp}(\mu ) = \Sigma$ and $\mu$ is absolutely continuous with respect to any area form on $\Sigma$;

• – measures $\mu$ such that $\operatorname {Supp}(\mu ) = X$ and $\mu$ is absolutely continuous with respect to any volume form on $X$.

Note that some or all of these categories may be empty.

Now assume furthermore that $X$ is a K3 or Enriques surface, that $X$ and $\Gamma$ are defined over $\mathbf {R}$, and consider the restriction of the action of $\Gamma$ on the real part $X(\mathbf {R})$ of $X$, which we assume to be non-empty. Fix a probability measure $\nu$ on $\Gamma$, whose support is a finite set generating $\Gamma$. Then, applying the results of [CD23c], this yields a classification and finiteness theorem for $\nu$-stationary measures on the real locus: the only $\nu$-stationary measures on $X(\mathbf {R})$ are convex combinations of the natural area forms of the components of $X(\mathbf {R})$, together with finitely many finite orbits.

1.6 Related recent results

Let us discuss a few related works which appeared after this work (and [CD23c]) were released.

Theorem A plays an important role in our more recent work [CD22], as it leads to global hyperbolicity properties of the dynamics on an open and dense set of Wehler surfaces, for the euclidean topology.

In [FT23], Filip and Tosatti use a similar blend of dynamics, analysis, and diophantine geometry to construct canonical currents and heights on some K3 surfaces $X$; as for generic Wehler surfaces, they assume that $\mathsf {Aut}(X)$ induces a lattice in the group of isometries of ${\mathrm {NS}}(X;\mathbf {Z})$ and that the genus $1$ fibrations on $X$ have no reducible fiber.

A recent paper of Corvaja, Tsimerman, and Zannier [PT23] studies ‘finite orbits’ of the group generated by a pair $(g,h)$ of parabolic automorphisms, with completely different methods. Their results are stronger than ours in some respects, since they conclude that there are only finitely many points $x$ for which $\{g^n h^m(x); n, m\in \mathbf {Z}\}$ is finite; thus, only a small part of the $\langle g,h \rangle$-orbit is assumed to be finite. But their assumptions are stronger (for instance, they exclude isotrivial fibrations); in particular, their technique does not lead to a complete classification of the situations where finite orbits are Zariski dense, as in Theorem B. A hope would be to combine our results with [PT23] to classify all pairs $(g,h)$ of parabolic automorphisms with a Zariski-dense set of common periodic points.

Finite $\mathsf {Aut}(X)$-orbits on Wehler surfaces (over arbitrary fields) are studied by Fuchs, Litman, Silverman, and Tran in [FLST23]. They study the structure of orbits over prime fields, and then construct complex examples with finite orbits of size as large as $288$.

1.7 Organization of the paper

We prove Theorem A in § 2, which is independent of the rest of the paper. Section 3 studies invariant curves for loxodromic automorphisms and non-elementary groups; we obtain an effective bound for the degree of a curve invariant under a loxodromic automorphism (see Proposition 3.7) and prove Theorem D. In § 4 we briefly discuss the case of tori and review the Kummer construction. The core of the paper is § 5, in which we develop the arithmetic method outlined above and establish Theorem B. Section 6 is devoted to consequences of Theorem B, and related comments. We prove Theorem C in § 7. Finally, canonical vector heights are discussed in § 8, where we solve Baragar's problem. Some open problems and possible extensions of our results are discussed in §§ 6.3 and 7.4.

2. Very general Wehler surfaces

Consider the family of Wehler surfaces described in § 3 of [CD23c] and [Bar04, Can01a, Kaw13, McM02]. In this section we prove Theorem A. For convenience, let us recall the statement of the theorem.

Theorem 2.1 If $X\subset \mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1$ is a very general Wehler surface, then $\mathsf {Aut}(X)$ does not preserve any non-empty, proper, and Zariski-closed subset of $X$.

Here, very general means that this property holds in the complement of a set of countably many hypersurfaces in the space of surfaces of degree $(2,2,2)$ in $\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1$. The proof follows from an elementary but tedious parameter counting argument. As shown in § 2.5, such a statement fails if $\mathsf {Aut}(X)$ is replaced by a thin non-elementary subgroup.

2.1 Notation and preliminaries

We use the notation of [CD23c, § 3]: $M=\mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1$, with affine coordinates $(x,y,z)$ (denoted $(x_1,x_2,x_3)$ in [CD23c]), $\pi _1$, $\pi _2$, and $\pi _3$ are the projections on the first, second, and third factors, and $\pi _{ij}$ is the projection $(\pi _i,\pi _j)$ onto $\mathbb {P}^1\times \mathbb {P}^1$. Then $L_i=\pi _i^*({\mathcal {O}}(1))$, $L=L_1^2\otimes L_2^2\otimes L_3^2$, and $X\subset M$ is a member of the linear system $\vert L \vert$. In the affine coordinates $(x,y,z)$, $X$ is defined by a polynomial equation of degree $(2,2,2)$, which we write

(2.1)\begin{equation} P(x,y,z) = A_{222} x^2y^2z^2+ A_{221} x^2y^2z + \cdots + A_{100}x + A_{010}y + A_{001}z + A_{000}. \end{equation}

Thus, $H^0(M,L)$ is of dimension $27$ and since the equation $\{ P=0 \}$ is defined up to multiplication by a complex scalar, the family of Wehler surfaces $X$ is $26$-dimensional. Modulo the action of $G = {\sf {PGL}}(2, \mathbf {C})^3$ they form an irreducible family of dimension $17$.

It was shown in [CD23c, § 3] that there exists a Zariski-open set $W_0\subset \vert L\vert$ of surfaces $X\in \vert L\vert$ such that:

1. (i) $X$ is a smooth K3 surface;

2. (ii) each of the three projections $(\pi _{ij})_X\colon X\to \mathbb {P}^1\times \mathbb {P}^1$ is a finite map, that is, $X$ does not contain any fiber of $\pi _{ij}\colon M\to \mathbb {P}^1\times \mathbb {P}^1$.

From now on, we suppose that $X$ belongs to $W_0$. Let $i$, $j$, and $k$ be three indices with $\{i,j,k\}=\{1,2,3\}$. Denote by $\sigma _i\colon X\to X$ the involution of $X$ that permutes the points in the fibers of the $2$-to-$1$ branched covering $(\pi _{jk})_X\colon X\to \mathbb {P}^1\times \mathbb {P}^1$. By [CD23c, § 3], the $\sigma _i$ generate a non-elementary subgroup of $\mathsf {Aut}(X)$. This subgroup is isomorphic to $\mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}$, it preserves the subspace of ${\mathrm {NS}}(X;\mathbf {Z})$ generated by the Chern classes of the $L_i$, and its action on this subspace is given by explicit matrices. Then $f_{ij}=\sigma _i\circ \sigma _j$ is a parabolic automorphism of $X$, preserving the genus $1$ fibration $\pi _k:X\to {\mathbb {P}^1}$. Moreover, if $X$ is very general the $L_i$ generate ${\mathrm {NS}}(X;\mathbf {Z})$.

2.2 Invariant curves

Proposition 2.2 If $X\in W_0$, $\mathsf {Aut}(X)$ does not preserve any algebraic curve.

This follows from the previous paragraph and the following more precise result.

Lemma 2.3 Let $X$ be a smooth Wehler surface. Assume that the three involutions $\sigma _i$ induce a faithful action of the group $\mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/ 2\mathbf {Z} \star \mathbf {Z}/2\mathbf {Z}$. Then the group generated by the $\sigma _i$ does not preserve any curve.

Proof. Assume that $C$ is an invariant curve. Since no curve can be contained simultaneously in fibers of $\pi _1$, $\pi _2$, and $\pi _3$, without loss of generality, we may suppose that $\pi _1\colon C\to \mathbb {P}^1(\mathbf {C})$ is dominant. Then the automorphism $f_{23}=\sigma _2\circ \sigma _3$ has finite order: indeed, on a general fiber $F$ of $\pi _1$, it acts as a translation that preserves the non-empty finite set $F\cap C$. This contradicts the fact that $f_{23}$ is parabolic and finishes the proof.

Thus, to prove Theorem 2.1, we are left to prove the non-existence of periodic orbits, which is the purpose of the following paragraphs.

2.3 Elliptic curves

Here we study $(2,2)$ curves in dimension 2. We keep notation as in § 2.1. Let us consider the line bundles $L_i=\pi _i^*({\mathcal {O}}(1))$ on $\mathbb {P}^1\times \mathbb {P}^1$ and set $L=L_1^2\otimes L_2^2$. Fix (affine) coordinates $(x,y)$ on $\mathbb {P}^1\times \mathbb {P}^1$, with $x$ and $y$ in $\mathbf {C} \cup \{\infty \}$. A curve $C\subset \mathbb {P}^1\times \mathbb {P}^1$ in the linear system $\vert L\vert$ is given by an equation of degree $(2,2)$ in $(x,y)$. Assume that $C$ contains the points $(0,0)$, $(\infty, 0)$, and $(0,\infty )$ and that it is smooth at the origin, with a tangent line given by $x+y=0$. Then its equation reduces to the form

(2.2)\begin{equation} \alpha x^2y^2 + \beta x^2y+ \gamma xy^2+\delta xy + \varepsilon (x+y)=0 \end{equation}

for some complex numbers $\alpha$, $\beta$, $\gamma$, $\delta$, and $\varepsilon$, with $\varepsilon \neq 0$. Denote this curve by $C_{(\alpha,\beta,\gamma,\delta,\varepsilon )}$. For a general choice of these parameters, $C$ is a smooth curve of genus $1$. We will need the following more precise result.

Lemma 2.4 Fix $(\beta, \gamma, \delta, \varepsilon )$ with $\varepsilon \neq 0$. Then for general $\alpha$, $C_{(\alpha,\beta,\gamma,\delta,\varepsilon )}$ is smooth.

Proof. An explicit calculation shows that the points of $C$ on $\{ \infty \}\times \mathbb {P}^1$ and $\mathbb {P}^1\times \{ \infty \}$ are smooth unless $\alpha = \beta =\gamma = 0$. Thus, for $\alpha \neq 0$, $C$ has no singular point at infinity. Now, viewing (2.2) as a quadratic equation in $x$ depending on the variable $y$, we can consider its discriminant $\Delta _x = \Delta _x(y)$; it is a polynomial of degree 4 in $y$ that detects fibers $\mathbf {C}\times \{ y \}$ intersecting $C$ at a single point (for those values $y$ for which $C\cap \mathbf {C}\times \{ y \}$ is contained in $\mathbf {C}^2$, that is, the polynomial in $x$ is of degree 2). It is easy to check that if $(x,y)$ is a singular point of $C$, then $y$ must be a multiple root of $\Delta _x$. Hence, if $y\mapsto \Delta _x(y)$ only has simple roots, $C$ is smooth in $\mathbf {C}^2$. Thus, it is enough to check that if $(\beta, \gamma, \delta, \varepsilon )$ is an arbitrary 4-tuple such that $\varepsilon \neq 0$, $\Delta _x$ has only simple roots for general $\alpha$. But $\Delta _x(y) = ay^4 +by^3+cy^2+{{\rm d}y}+e$, where only $b$ depends on $\alpha$, with $b(\alpha ) = 2\gamma \delta - 4\alpha \varepsilon$, and $e=\varepsilon ^2\neq 0$. Now the discriminant of $\Delta _x$, as a degree $4$ polynomial in $y$, is a polynomial expression in $(a,b,c,d,e)$, and as a polynomial in $b$ it has a unique leading term $27b^4e^2$. Thus, $(\beta, \gamma, \delta, \varepsilon )$ being fixed, with $\varepsilon \neq 0$, this discriminant depends non-trivially on $\alpha$; for a general $\alpha$, this discriminant is not zero, thus $\Delta _x$ has four distinct roots, so that $C$ is smooth, as was to be proved.

There are two involutions $\sigma _1$ and $\sigma _2$ on $C$, respectively, permuting the points in the fibers of the projections $(\pi _2)_{\vert C}\colon C\to \mathbb {P}^1$ and $(\pi _1)_{\vert C}\colon C\to \mathbb {P}^1$; that is, $\sigma _i$ changes the $i$th coordinate, while keeping the others unchanged. The composition $f=\sigma _1\circ \sigma _2$ is a translation on $C$ mapping $(0,\infty )$ to $(\infty, 0)$; in particular, $f$ is not the identity.

Lemma 2.5 Fix $(\beta, \gamma, \delta, \varepsilon )$ with $\varepsilon \neq 0$ and assume that the curve $C_{(0,\beta,\gamma,\delta,\varepsilon )}$ is smooth. Then the dynamics of the translation $f$ on $C_{(\alpha,\beta,\gamma,\delta,\varepsilon )}$ varies non-trivially with $\alpha$: it is periodic for a countable dense set of $\alpha$'s, and non-periodic for the other parameters.

Proof. For $\alpha$ in the complement of a finite set, $C_\alpha :=C_{(\alpha,\beta,\gamma,\delta,\varepsilon )}$ is a smooth curve of genus $1$, and $f$ acts as a translation on $C_\alpha$. Let us analyze the orbit of $(0, \infty )$. Denote by $u, v\in \mathbf {C}\cup \{\infty \}$ the complex numbers such that $\sigma _2(\infty,0)=(\infty,v)$ and $(u,v)=\sigma _1(\infty,v)=f^2(0,\infty )$. The translation $f$ is periodic of period $2$ if and only if $(u,v)=(0,\infty )$, if and only if $(\infty,\infty )$ is a point of $C_\alpha$, if and only if $\alpha =0$. Hence, $f$ is periodic of period $2$ on $C_0$ but after perturbation it is not of period $2$ anymore. For small $\alpha$ we can write $C=\mathbf {C}/\Lambda _\alpha$ for some lattice $\Lambda _\alpha =\mathbf {Z}+\mathbf {Z}\tau (C_\alpha )$ and $f(z)=z+t(C_\alpha )$, with $t(C_\alpha )$ and $\tau (C_\alpha )$ depending holomorphically on the parameters $\alpha$. If we further decompose $t(C_\alpha )=a(C_\alpha )+b(C_\alpha )\tau (C_\alpha )$, where $a$ and $b$ are two real analytic functions with values in $\mathbf {R}$, then both $a$ and $b$ must be non-constant. Indeed if one of them were constant, then the other would be a non-constant real holomorphic function, which is impossible (see [Can01b, Proposition 2.2] for a similar argument). The result follows.

2.4 Proof of Theorem 2.1

2.4.1 From finite orbits to fixed points

Let us form the universal family ${\mathcal {X}}\subset W_0\times M$, where $W_0\subset \vert L\vert$ is the open set defined in § 2.1: the fiber of the projection ${\mathcal {X}}\to W_0$ above $X\in W_0$ is precisely the surface $X\subset M$. The group $\mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}$ acts by automorphisms on ${\mathcal {X}}$, preserving each fiber of ${\mathcal {X}}\to W_0$: the generators of the first, second, and third $\mathbf {Z}/2\mathbf {Z}$ factors give rise to involutions ${\widetilde {\sigma }}_1$, ${\widetilde {\sigma }}_2$, and ${\widetilde {\sigma }}_3$ which, when restricted to a fiber $X$, correspond to the automorphisms $\sigma _i\in \mathsf {Aut}(X)$. These involutions ${\widetilde {\sigma }}_i$ extend to birational involutions of the Zariski closure ${\overline {\mathcal {X}}}\subset \vert L \vert \times M$.

Remark 2.6 If $X\in \vert L\vert$ is smooth and contains a fiber $V=\{(x_0,y_0)\}\times \mathbb {P}^1\subset X$ of $\pi _{12}$, the curve $V$ is contained in the indeterminacy locus of ${\tilde {\sigma }}_3$ (one may consult [CO15] for further results: see Theorem 3.3 and the proof of its third and fourth assertions).

Consider the group $\mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}$ acting on ${\mathcal {X}}$. Its restriction to the fiber $X$ gives a subgroup $\Gamma$ of $\mathsf {Aut}(X)$. Let $d$ be a positive integer. There are only finitely many homomorphisms from $\mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}$ to groups of order $\leq d!$, and the intersection of the kernels of these homomorphisms is a normal subgroup of finite index. Denote by $\Gamma _d$ the corresponding subgroup of $\mathsf {Aut}(X)$. If $\Gamma$ has an orbit of cardinality $\leq d$ on some surface $X$, then this orbit is fixed pointwise by $\Gamma _{d}$. Let us introduce the subvariety

(2.3)\begin{equation} {\mathcal{Z}}_d = \{ (X,x);\ x\in X\ {\text{and }} \forall f \in \Gamma_{d},\ f(x)=x \}\subset {\mathcal{X}}. \end{equation}

Since ${\mathcal {X}}\to W_0$ is proper, from this discussion we obtain the following.

Lemma 2.7 The following properties are equivalent:

1. (1) for a very general surface $X\in \vert L\vert$, every orbit of $\Gamma$ in $X$ is infinite;

2. (2) for every $d\geq 1$, the projection ${\mathcal {Z}}_d \to W_0$ is not surjective;

2.4.2 Preparation

According to Lemma 2.7, to prove Theorem 2.1 it suffices to show that the projection of ${\mathcal {Z}}_d\subset {\mathcal {X}}$ onto $W_0$ is a proper subset for every $d\geq 1$. Thus, let us assume that there is an integer $d$ for which ${\mathcal {Z}}_d$ surjects onto $W_0$ and seek for a contradiction. Pick a small open subset $U\subset W_0$ for the Euclidean topology, over which one can choose a holomorphic section $s\colon X\mapsto s_X$ of ${\mathcal {X}}\to W_0$ such that $s_X$ is fixed by $\Gamma _{d}$; equivalently, the image of $s$ is contained in ${\mathcal {Z}}_d$.

The group $G= {\sf {PGL}}_2(\mathbf {C})\times {\sf {PGL}}_2(\mathbf {C})\times {\sf {PGL}}_2(\mathbf {C})$ acts on $M$ and on $\vert L \vert$, preserving $W_0$. Recall that modulo the action of this group, the space of Wehler surfaces is irreducible and of dimension $17$.

2.4.3 Case 1

Let us first assume that we can find $U$ such that $s_X$ is not fixed by ${\tilde {\sigma }}_1$, ${\tilde {\sigma }}_2$, nor ${\tilde {\sigma }}_3$. As in Lemma 2.4 this implies that for each pair of indices $i\neq j$, the fiber $C$ of $(\pi _i)_X\colon X\to \mathbb {P}^1$ through $s_X$ is smooth near $s_X$ and $s_X\in C$ is not a ramification point of the projection $(\pi _j)_{\vert C} \colon C\to \mathbb {P}^1$. As in § 2.1, fix coordinates $(x,y,z)$ on $M=(\mathbb {P}^1)^3$ with $x$, $y$, and $z$ in $\mathbf {C}\cup \{\infty \}$. Modulo the action of $G$, we may assume that for every $X$ in $U$:

1. (a) the point $s_X$ is the point $(0,0,0)$ in $(\mathbb {P}^1)^3$;

2. (b) $X$ contains $(\infty, 0, 0)$, $(0,\infty, 0)$, and $(0,0,\infty )$;

3. (c) the tangent plane to $X$ at the origin is given by the equation $x+y+z=0$;

4. (d) the coefficients of $x^2y^2z^2$ and $x$, $y$ and $z$ in the equation of $X$ are all equal to the same complex number.

Note that assumption (a) can be achieved by a single translation, assumption (b) can be obtained by transformations of the form $(x,y, z) \mapsto ({x}/({x-\alpha }), {y}/({y-\beta }), {z}/({z - \gamma }))$, assumption (c) is achieved by the action of diagonal maps (note that by our assumption, the tangent plane to $X$ at the origin $s_X=(0,0,0)$ cannot be one of the coordinate planes), and then we obtain assumption (d) by the action of homotheties. After such a conjugation, the equation of $X$ is of the form

(2.4)\begin{align} & A x^2y^2z^2 + B x^2 y^2 z+ B' x^2 y z^2+ B'' x y^2z^2 + C x^2y z + C' x y^2 z+ C'' xyz^2 \nonumber\\ &\quad + Dx^2y^2+D'x^2z^2+D''y^2z^2+ E xyz \nonumber\\ &\quad + F x^2 y + F' x^2 z + F'' x y^2 + F''' y^2 z + F^{iv} x z^2 + F^{v} yz^2 \nonumber\\ &\quad + G xy + G' xz + G'' yz+ A(x+y+z)=0. \end{align}

Since this equation is defined up to multiplication by an element of $\mathbf {C}^*$, we are left with 19 parameters. The automorphism $f_{12}=\sigma _1\circ \sigma _2$ preserves the genus $1$ fibration $(\pi _3)_{\vert X}\colon X\to \mathbb {P}^1$. The fiber of $(\pi _3)_{\vert X}$ through $(0,0,0)$ is a curve $C\subset \mathbb {P}^1\times \mathbb {P}^1$ given by the equation

(2.5)\begin{equation} Dx^2 y^2+ F x^2 y + F'' x y^2 + G xy + A(x+y)=0. \end{equation}

Two cases need to be considered, depending on the smoothness of this curve.

• – If this curve is singular, by Lemma 2.4 the coefficients in (2.5) satisfy a non-trivial relation of the form $P_3(D, F, F'', G, A) = 0$.

• – If it is smooth, consider an iterate $f_{12}^m$ of $f_{12}$ in $\Gamma _d$, with $1\leq m\leq d!$; then $f_{12}^m$ is a translation of the genus $1$ curve $C$ that fixes $s_X$, so that it fixes $C$ pointwise. From Lemma 2.5, the coefficients in (2.5) satisfy a relation of the form $Q_3(D, F, F'', G, A) = 0$.

In both cases we get a relation of the form $R_3(D, F, F'', G, A) = 0$ (with $R_3 = P_3$ or $Q_3$) that depends non-trivially on the first factor. Similarly, looking at the dynamics of $f_{23}=\sigma _2\circ \sigma _3$ and $f_{31}=\sigma _3\circ \sigma _1$, we obtain two further relations of the form $R_1(D'', F'', F^v, G'', A) = 0$ and $R_2(D', F',F^{iv}, G', A) = 0$.

We claim that the subset defined by these 3 constraints is of codimension 3: indeed, if we look at the subvariety cut out by the equations $R_i = 0$, $i=1, 2, 3$ and slice it by a 3-plane corresponding to the coordinates $D$, $D'$, and $D''$, then by Lemmas 2.4 and 2.5 and the independence of variables, this slice is reduced to a point. This shows that the image of the section $X\mapsto s_X$ has dimension ${\leq }16$, which contradicts the fact that $W_0/G$ is of pure dimension $17$. Thus, our hypothesis on ${\mathcal {Z}}_d$ cannot be true and Case 1 does not hold.

2.4.4 Case 2

If Case 1 does not hold, every point $(X,(x,y,z))$ of ${\mathcal {Z}}_d$ has the property: $(x,y,z)\in X$ is a ramification point for at least one of the three projections $(\pi _i)_{\vert X}$. Equivalently, every point of the finite orbit $F=\Gamma _d(s_X)\subset X$ is fixed by at least one of the three involutions $\sigma _i$. This case is simpler, since a direct count of parameters will lead to a contradiction.

$\bullet$ If a point of $F$ were a ramification point of each $(\pi _i)_{\vert X}$, this point would be a singularity of $X$, and $X$ would not be in $W_0$. Thus, each point of $F$ is a ramification point for at least one and at most $2$ of the projections.

$\bullet$ Now, assume that every point of $F$ is a ramification point for exactly $2$ of the projections. Choose a local section $s_X$ of ${\mathcal {Z}}_d$ above a small open set $U\subset W_0$ (for the Euclidean topology), as in § 2.4.3. Permuting the coordinates and using a translation in $G$, we assume that $s_X=(0,0,0)$ and $s_X$ is fixed by $\sigma _2$ and $\sigma _3$. After this normalization, with notation as in (2.1), we have $A_{010}= A_{001} = A_{000}=0$. Let $s_X'=\sigma _1(s_X)$; this point is not equal to $s_X$ because otherwise $X$ would be singular at $s_X$. Thus, we may use a transformation of the form $x\mapsto {x}/({x-\alpha })$ in $G$ to assume that $s_X'=(\infty, 0,0)$ (i.e. $A_{200} = 0$). Now by our assumption, this second point must be fixed by $\sigma _2$ and $\sigma _3$, which imposes two more constraints ($A_{201} = A_{210} =0$). Now, consider the curve $C_1\subset X$ defined by the equation $x=0$. Using elements of $G$ acting on $y$ and $z$ by $y\mapsto {y}/({y-\beta })$ and $z\mapsto {z}/({z-\gamma })$, we may assume that $(0,\infty,\infty )$ is on $C_1$ and is a ramification point for $(\pi _2)_{\vert C_1}$. With such a choice, the coefficients of $y^2z^2$ and $y^2z$ vanish. At this stage we did not use the diagonal action of $(\mathbf {C}^*)^3$, which stabilizes $(0,0,0)$, $(\infty, 0,0)$, and $(0, \infty, \infty )$. With this we can impose for instance the same non-zero coefficients for the terms $xy$, $yz$, and $zx$, so we end up with $17$ coefficients, hence at most $16$ free parameters. Again this contradicts the fact that $\dim (W_0)=17$.

$\bullet$ Now, assume that one of the points of the finite orbit $F$ is fixed by $\sigma _3$ but not by $\sigma _1$ and $\sigma _2$. The analysis is similar to that of the previous case. We may choose this point to be $s_X$, and using the group $G$, we can arrange that $s_X=(0,0,0)$, $\sigma _1(s_X)=(\infty, 0,0)$, and $\sigma _2(s_X)=(0,\infty,0)$; with the notation from (2.1), this means $A_{000} = A_{200} = A_{020} = 0$. In addition $A_{001} = 0$ because $(0,0,0)$ is fixed by $\sigma _3$. By our hypothesis, $(\infty, 0,0)$ is fixed by $\sigma _2$ or $\sigma _3$ (or both). This implies that at least one of $A_{210}$ or $A_{201}$ vanishes. Likewise $A_{120}A_{021} = 0$. Now consider the curve $C_2\subset X$ given by $y=0$. Given the constraints already listed, the equation of $C_2$ can be written as

(2.6)\begin{equation} \alpha x^2z^2 + \beta x^2 z+\gamma xz^2+ \delta xz + \varepsilon z^2 + \iota x = 0. \end{equation}

There are $4$ ramification points for $(\pi _1)_{\vert C_2}$, counting with multiplicities, and none of them satisfies $z=0$. Thus, using $z\mapsto {z}/({z-\gamma })$ and $x\to \lambda x$ we may put one of them at $(1,0,\infty )$. This imposes $\alpha + \gamma + \varepsilon =0$ and $\beta + \delta =0$.

Finally, we may still use the subgroup $\{\mathrm {Id}\}\times \mathbf {C}^*\times \mathbf {C}^*\subset G$, which fixes the four points $(0,0,0)$, $(\infty, 0, 0)$, $(0, \infty, 0)$, and $(1, 0,\infty )$, to assume that the non-zero coefficients in front of $yz$, $xz$, and $z^2$ are equal. In conclusion, under our assumption we have found at least $10$ independent linear constraints on the coefficients of the Wehler surface so again at most $16$ free parameters remain.

Thus, in all cases we get a contradiction, and the proof of Theorem 2.1 is complete.

2.5 Examples

2.5.1

Consider the subgroup $H$ of $\mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}$ generated by $f_{23}^m$ and $f_{31}^m$, for some large positive integer $m$ (as above, $f_{23}=\sigma _2\circ \sigma _3$, $f_{31}=\sigma _3\circ \sigma _1$). The automorphism $f_{23}$ preserves the fibers of the projection $(\pi _1)_{\vert X}$ and its periodic points form a dense set of fibers (see [Can01b, CD23b] or § 3.1.1 here). The intersection number between a fiber of $(\pi _1)_{\vert X}$ and a fiber of $(\pi _2)_{\vert X}$ is equal to $2$. Thus, if $m$ is big enough, $f_{23}^m$ and $f_{31}^m$ share a common fixed point (in fact, $\simeq c m^4$ common fixed points, for some $c>0$ as $m$ goes to $+\infty$). If $X\in W_0$, $\langle f_{23}^m, f_{31}^m\rangle$ is non-elementary because the class $c_1\in {\mathrm {NS}}(X;\mathbf {Z})$ of the invariant fibration of $f_{23}$ is not fixed by $f_{31}$, and vice versa (see also Lemma 3.13). Taking a surface $X\in W_0$ that is defined over $\mathbf {Q}$, we get, in particular, the following.

Proposition 2.8 For every integer $N\geq 0$, there is a smooth Wehler surface $X$ defined over $\mathbf {Q}$ and a non-elementary subgroup $\Gamma$ of $\mathsf {Aut}(X_\mathbf {Q})$ with at least $N$ fixed points.

Remark 2.9 If $X\in W_0$ and $m\geq 1$, the group $\langle f_{23}^m, f_{31}^m\rangle$ has infinite index in $\mathsf {Aut}(X)$. Indeed, the index of $\langle (\sigma _2\circ \sigma _3)^m, (\sigma _3\circ \sigma _1)^m\rangle$ in $\mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}\star \mathbf {Z}/2\mathbf {Z}$ is infinite.

2.5.2

Let us construct smooth Wehler surfaces for which the subgroup $\Gamma$ of $\mathsf {Aut}(X)$ generated by the three involutions $\sigma _i$ has a finite orbit. Using affine coordinates $(x,y,z)$ for $(\mathbb {P}^1)^3$, set $V=\{(\varepsilon _1, \varepsilon _2,\varepsilon _3);\ \varepsilon _i \in \{ 0, \infty \}\ \forall i=1,2,3\}$. Observe that if $V$ is contained in a Wehler surface $X$, then $V$ is an orbit of $\Gamma$ of size $8$. Now, writing the equation of $X$ as in (2.1), $V\subset X$ if and only if $A_{ijk}=0$ for all triples $(i, j, k)\in \{0,2\}^3$. The corresponding linear system has no base points, except from the points of $V$. If $(A_{100}, A_{010},A_{001})\neq (0,0,0)$, the surface is smooth at the base point $(0,0,0)$. The smoothness at the other 7 points of $V$ is determined by similar constraints on the coefficients $A_{ijk}$: for instance, the smoothness at the point $(\infty, 0,0)$ is equivalent to $(A_{210}, A_{201}, A_{100})\neq (0,0,0)$. Thus, the theorem of Bertini shows that a general member of the family of Wehler surfaces containing $V$ is smooth, and the result follows.

3. Non-elementary groups and invariant curves

The main purpose of this section is to establish the following.

Theorem 4 Let $X$ be a compact Kähler surface and let $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$ containing a loxodromic element. Then there exists a loxodromic element $f$ in $\Gamma$ such that every $f$-periodic curve is $\Gamma$-periodic.

Along the way, some results of independent interest will be obtained: Proposition 3.7, which will be used in § 7, gives an effective bound for the degree of a periodic curve under a loxodromic automorphism; Proposition 3.9 provides a singular model of $(X, \Gamma )$ without $\Gamma$-periodic curves, and discusses ampleness properties of some line bundles. This model will be crucial for the study of the dynamical heights in § 5.

3.1 Preliminaries

Let $X$ be a compact Kähler surface. By the Hodge index theorem, the intersection form $\langle \cdot \vert \cdot \rangle$ is non-degenerate and of signature $(1, h^{1,1}(X)-1)$ on $H^{1,1}(X;\mathbf {R})$; its isotropic cone is the set of vectors $u\in H^{1,1}(X;\mathbf {R})$ with $\langle u\vert u \rangle =0$. Fix a Kähler form $\kappa _0$ on $X$, with $\int _X \kappa _0\wedge \kappa _0=1$, denote its class by $[\kappa _0]$, and define the positive cone in $H^{1,1}(X;\mathbf {R})$ to be the set

(3.1)\begin{equation} {\mathrm{Pos}}(X)=\{u\in H^{1,1}(X;\mathbf{R});\ \langle u\vert u\rangle >0\ {\text{and}}\ \langle [\kappa_0] \vert u\rangle >0\}. \end{equation}

Equivalently, ${\mathrm {Pos}}(X)$ is the connected component of $\{ u\in H^{1,1}(X;\mathbf {R});\ \langle u\vert u\rangle >0\}$ containing Kähler forms; in particular, its definition does not depend on $\kappa _0$. This cone ${\mathrm {Pos}}(X)$ contains one of the two connected components, denoted $\mathbb {H}_X$, of the hyperboloid $\{ u\in H^{1,1}(X;\mathbf {R});\ \langle u\vert u\rangle =1 \}$; we can identify $\mathbb {H}_X\!$ with its projection $\mathbb {P}(\mathbb {H}_X)$ in the projective space $\mathbb {P}(H^{1,1}(X;\mathbf {R}))$, and in doing so we get $\mathbb {H}_X\simeq \mathbb {P}(\mathbb {H}_X)= \mathbb {P}({\mathrm {Pos}}(X))$. Via this identification, the Hilbert metric on $\mathbb {H}_X$ coincides with the hyperbolic metric induced by the intersection form (see [CD23c, § 2]), and the boundary $\partial \mathbb {H}_X$ is identified to the projection of the isotropic cone in $\mathbb {P}(H^{1,1}(X;\mathbf {R}))$.

Forgetting about torsion, $H^2(X;\mathbf {Z})\cap H^{1,1}(X;\mathbf {R})$ can be identified with the Néron–Severi group ${\mathrm {NS}}(X;\mathbf {Z})$; thus, we shall consider ${\mathrm {NS}}(X;\mathbf {R})$ as a subspace of $H^{1,1}(X;\mathbf {R})$.

An automorphism of $X$ has a type (elliptic, parabolic, or loxodromic) according to the type of its induced action on $\mathbb {H}_X$. Given a subgroup $\Gamma \leq \mathsf {Aut}(X)$, we denote by $\Gamma _{\mathrm {par}}$ (respectively, $\Gamma _{\mathrm {lox}}$) the set of parabolic (respectively, loxodromic) automorphisms in $\Gamma$.

3.1.1 Parabolic automorphisms

If $g$ is parabolic, it permutes the fibers of a genus-$1$ fibration $\pi _g\colon X\to B_g$, and induces an automorphism $\overline {g}$ of the curve $B_g$. The induced automorphism $\overline {g}$ has finite order, except maybe when $X$ is a torus $\mathbf {C}^2/\Lambda$ (see [CF03, Proposition 3.6]).

If $\overline {g}$ is the identity, then $g$ preserves each fiber of $\pi _g$, acting as a translation on each smooth fiber. If $U_0$ is a disk in $B_g$ that does not contain any critical value of $\pi _g$, the universal cover of $\pi _g^{-1}(U_0)$ is holomorphically equivalent to $U_0\times \mathbf {C}$, with its fundamental group $\mathbf {Z}^2$ acting by $(x,y)\in U_0\times \mathbf {C}\mapsto (x,y+a+b\tau (x))$ for every $(a,b) \in \mathbf {Z}^2$, where $\tau \colon U_0\to \mathbf {C}$ is a holomorphic function taking its values in the upper half plane. In these coordinates $g$ lifts to a diffeomorphism $\tilde {g}(x,y)=(x,y+t(x))$ for some holomorphic function $t\colon U_0\to \mathbf {C}$. The $m$th iterate $g^m$ fixes pointwise a fiber $\{x\}\times \mathbf {C}/(\mathbf {Z}\oplus \mathbf {Z}\tau (x))$ if and only if $mt(x)\in \mathbf {Z}\oplus \mathbf {Z} \tau (x)$. The union of such fibers, for all $m\geq 1$, form a dense subset of $X$. This comes from the fact that ‘$t$ varies independently from $\tau$’, a property which implies also that the differential of $g^m$ at a fixed point is, except for finitely many fibers, a $2\times 2$ upper triangular matrix with ones on the diagonal and a non-trivial lower left coefficient. We refer to [Can01b, Can14, CD23b], and to the proof of Theorem 5.15 for a slightly different viewpoint on this property, using real-analytic coordinates.

The induced action $g^*$ on $H^{1,1}(X;\mathbf {R})$ admits a simple description: if $F$ is any fiber of $\pi _g$, its class $[F]\in H^{1,1}(X;\mathbf {R})$ is fixed by $g^*$, the ray $\mathbf {R}_+[F]$ is contained in the isotropic cone, and $ ({1}/{n^2})(g^n)^*w$ converges towards a positive multiple of $[F]$ for every $w\in {\mathrm {Pos}}(X)$. In particular, the class $[F]$ is nef. Regarding the induced action on $\mathbb {H}_X$, $\mathbb {P}([F])$ is the unique fixed point of the parabolic map $g^*$ on $\mathbb {H}_X\cup \partial \mathbb {H}_X$ (see [Can01b, Can14, CD23b]).

Recall that a linear endomorphism of a vector space is unipotent if all its eigenvalues $\alpha \in \mathbf {C}$ are equal to $1$; it is virtually unipotent if some of is positive iterates is unipotent. Since the topological entropy of $g$ vanishes, Lemma 2.6 of [CP21] gives the following.²

Lemma 3.1 Let $X$ be a complex projective surface. If $g\in \mathsf {Aut}(X)$ is parabolic, then $g^*$ is virtually unipotent, both on ${\mathrm {NS}}(X;\mathbf {R})$ and on $H^2(X;\mathbf {R})$.

3.1.2 Loxodromic automorphisms

The dynamics of a loxodromic automorphism $f$ is much richer (see [Can14]). The isolated periodic points of $f$ of period $m$ equidistribute towards a probability measure $\mu _f$ as $m$ goes to $+\infty$, the topological entropy of $f$ is positive, and $\mu _f$ is the unique ergodic, $f$-invariant probability measure of maximal entropy.

We denote by $\lambda (f)$ the spectral radius of the induced automorphism $f^*$ on $H^{1,1}(X)$, which is larger than 1. Then $\lambda (f)$ and $1/\lambda (f)$ are eigenvalues of $f^*$ with multiplicity $1$, with respective nef eigenvectors $\theta _f^+$ and $\theta _f^-$ which are isotropic and generate an $f^*$-invariant plane $\Pi _f\subset H^{1,1}(X;\mathbf {R})$ (see Figure 1). Their projectivizations are the two fixed points on $\partial \mathbb {H}_X$ of the induced loxodromic isometry of $\mathbb {H}_X$. The remaining eigenvalues have modulus $1$. We normalize the eigenvectors $\theta ^{\pm }_f$ by imposing

(3.2)\begin{equation} \langle \theta_f^+\vert [\kappa_0] \rangle= \langle \theta_f^-\vert [\kappa_0] \rangle= 1, \end{equation}

where $\kappa _0$ is the Kähler form introduced at the beginning of § 3.1 (recall that $\langle [\kappa _0]\vert [\kappa _0]\rangle =1$). We set $m_f=\frac {1}{2} ({\theta _f^++\theta _f^-})$. With such a choice, $\langle {m_f\vert m_f}\rangle = \frac {1}{2} \langle \theta _f^+\vert \theta _f^-\rangle >0$.

Remark 3.2 Denote by ${\mathrm {Ang}}_{\kappa _0}(\theta ^+_f, \theta ^-_f)$ the visual angle between the boundary points $\mathbb {P}(\theta ^+_f)$ and $\mathbb {P}(\theta ^-_f)$, as seen from $[\kappa _0]$ (or $\mathbb {P}([\kappa _0])$). Then

(3.3)\begin{equation} \langle{m_f\vert m_f}\rangle =\big(\sin\big(\tfrac{1}{2}{\mathrm{Ang}}_{\kappa_0} (\theta^+_f, \theta^-_f)\big)\big)^2=\tfrac{1}{2} (1-\cos({\mathrm{Ang}}_{\kappa_0}(\theta^+_f, \theta^-_f))), \end{equation}

so, in particular, $0 < \langle m_f\vert m_f\rangle \leq 1$, and the right-hand inequality is an equality if and only if $m_f= [\kappa _0]$.³ In $\mathbb {H}_X$, the geodesic joining $\mathbb {P}(\theta ^-_f)$ and $\mathbb {P}(\theta ^+_f)$ is the curve $\mathsf {Ax}(f)$ parametrized by $s\theta ^+_f+t\theta ^-_f$ with $s\in \mathbf {R}_+^*$ and $st=\langle \theta ^+_f\vert \theta ^-_f\rangle ^{-1}$. The projection of $[\kappa _0]$ on $\mathsf {Ax}(f)$ is $ ({\sqrt {2}}/{\langle \theta ^+_f\vert \theta ^-_f\rangle ^{1/2}})m_f$ and, by [BC16, Lemma 6.3], we have

(3.4)\begin{equation} \cosh(\operatorname{d}_{\mathbb{H}}([\kappa_0], \mathsf{Ax}(f)))=\frac{\sqrt{2}}{\langle \theta^+_f\vert \theta^-_f\rangle^{1/2}}. \end{equation}

Figure 1. Left: a picture of ${\mathrm {NS}}(X;\mathbf {R})$ in case $\rho (X)=3$. The highlighted plane is $\Pi _f$, it intersects the isotropic cone along the lines $\mathbf {R}\theta _f^+$ and $\mathbf {R}\theta _f^-$; the line outside the cone is $\Pi _f^\perp$, the central point is $[\kappa _0]$. If $f$ preserves a curve $E$, its class lies on $\Pi _f^\perp$. Right: a projective view of the same picture, where the two tangent lines are the projectivizations of the planes $(\theta _f^+)^\perp$ and $(\theta _f^-)^\perp$.

3.1.3 Non-elementary subgroups of $\mathsf {Aut}(X)$

See [CD23c, § 2.3] for more details about the results of this paragraph. By definition, a subgroup $\Gamma \subset \mathsf {Aut}(X)$ is non-elementary if it acts on $\mathbb {H}_X$ as a non-elementary group of isometries or, equivalently, if it contains a non-abelian free group, all of whose elements $f\neq {\rm id}$ are loxodromic. Such a group $\Gamma \subset \mathsf {Aut}(X)$ preserves a unique subspace $\Pi _\Gamma \subset H^{1,1}(X;\mathbf {R})$ on which: (i) $\Gamma$ acts strongly irreducibly and (ii) the intersection form induces a Minkowski form. Moreover, $\Pi _\Gamma =\Pi _{\Gamma _0}$ for any finite index subgroup of $\Gamma$.

Each of the following conditions implies that $\Gamma$ is non-elementary:

• – $\Gamma$ contains a pair of loxodromic elements $(f,g)$ with $\{ \theta _f^+, \theta _f^- \}\cap \{ \theta _g^+, \theta _g^- \} = \emptyset$;

• – $\Gamma$ contains two parabolic elements associated to different fibrations; equivalently, $\Gamma$ contains a parabolic and a loxodromic element.

If $\mathsf {Aut}(X)$ contains a non-elementary group $\Gamma$, then $X$ is automatically projective and $\Pi _\Gamma$ is contained in the Néron–Severi group ${\mathrm {NS}}(X;\mathbf {R})$ (see [CD23a]). If, in addition, $\Gamma$ contains a parabolic element, then $\Pi _\Gamma$ is defined over $\mathbf {Q}$ with respect to the lattice ${\mathrm {NS}}(X;\mathbf {Z})$ (see [CD23c, Lemma 2.9]).

The limit set $\operatorname {Lim}(\Gamma )\subset \partial \mathbb {H}_X$ is the closure of the set of fixed points of loxodromic elements in $\mathbb {P}(\Pi _\Gamma )$, or equivalently the smallest closed invariant subset in $\partial \mathbb {H}_X$. The following lemma is well known (see [Kap01, Lemma 3.24]).

Lemma 3.3 If $\Gamma$ is non-elementary, $\{ (\mathbb {P}(\theta ^+_f), \mathbb {P}(\theta ^-_f));\ f\in \Gamma _{\mathrm {lox}} \}$ is dense in $\operatorname {Lim}(\Gamma )^2$.

3.2 Periodic curves of loxodromic automorphisms

Fix a loxodromic automorphism $f\colon X\to X$. Our purpose in this paragraph is to bound the degree of the periodic curves of $f$.

Lemma 3.4 Let $e$ be an element of $H^{1,1}(X;\mathbf {R})$ such that $e$ is orthogonal to $m_f$ and $\langle [\kappa _0]\vert e\rangle = 1$. Then $\langle e \vert e \rangle < 0$ and

\[ -\langle e \vert e \rangle \geq \frac{\langle{m_f\vert m_f}\rangle}{1- \langle{m_f\vert m_f}\rangle}=\bigg(\tan\bigg(\frac{1}{2}{\mathrm{Ang}}_{\kappa_0} (\theta^+_f,\theta^-_f)\bigg)\bigg)^2. \]

Note that under the assumption of the lemma $m_f$ cannot be equal to $[\kappa _0]$, so $0 < \langle {m_f\vert m_f}\rangle <1$ by Remark 3.2.

Proof. Write $m_f=[\kappa _0]+v$ and $e=[\kappa _0]+w$ where $v$ and $w$ are in the orthogonal complement $[\kappa _0]^\perp$. Then, $\langle e \vert m_f\rangle =0$, so $\langle v\vert w\rangle =-1$, and the Cauchy–Schwarz inequality gives $1 \leq (-\langle v\vert v\rangle )(-\langle w\vert w\rangle )$ because the intersection form is negative definite on $[\kappa _0]^\perp$. This inequality is equivalent to $1\leq (1-\langle m_f\vert m_f\rangle )(1-\langle e\vert e\rangle )$ and the result follows.

If $C\subset X$ is a curve, define its degree (with respect to $\kappa _0$) to be

(3.5)\begin{equation} \deg (C) = \int_C \kappa_0 =\langle [C] \vert [\kappa_0] \rangle, \end{equation}

and similarly define the degree of an automorphism $g\in \mathsf {Aut}(X)$ by

(3.6)\begin{equation} \deg (g) = \int_X \kappa_0\wedge g^*\kappa_0 =\langle [\kappa_0]\vert g^*[\kappa_0]\rangle. \end{equation}

In the following lemma, $K_X$ denotes the canonical bundle of $X$.

Lemma 3.5 Let $c_X\geq 0$ be a constant such that $\langle K_X\vert \cdot \rangle \leq c_X \langle [ \kappa _0]\vert \cdot \rangle$ on the effective cone. If $f\in \mathsf {Aut}(X)$ is loxodromic and $E$ is a reduced, connected, and $f$-periodic curve, then

\[ \langle{\theta_f^+\vert \theta_f^-}\rangle \deg(E)\leq 2(1+ c_X). \]

If $E$ is not connected, then $E$ has at most $\rho (X)-2$ connected components, thus

\[ \langle{\theta_f^+\vert \theta_f^-}\rangle \deg(E)\leq 2(\rho(X)-2)(1+c_X)\leq 2(b_2(X)-2)(1+c_X), \]

where $\rho (X)$ is the Picard number of $X$ and $b_2(X)$ is its second Betti number.

If $E$ is $f$-invariant, then $[E]$ is orthogonal to $\Pi _f$ for the intersection form, so the Hodge index theorem implies that $[E]^2<0$. Thus, if $E$ is irreducible, it is determined by its class $[E]$, and Lemma 3.5 shows that $f$ has only finitely many irreducible periodic curves; this finiteness result strengthens [Kaw08, Proposition B] (see also [Can01a] and [Can14, Proposition 4.1]). We denote by $D_f$ the union of these irreducible $f$-periodic curves.

Example 3.6 We can take $c_X=0$ when $X$ is a K3, Enriques, or abelian surface.

Proof of Lemma 3.5 Assume first that $E$ is connected. Set $e= {[E]}/{\deg (E)}$ so that ${\langle e\vert [\kappa _0] \rangle = 1}$. Since $E$ is reduced and connected, its arithmetic genus $\langle K_X+ E\vert E\rangle +2$ is non-negative (see [BHPV04, § II.11]), so

(3.7)\begin{equation} -\langle{E\vert E}\rangle \leq 2+ \langle K_X \vert E\rangle \leq 2+ c_X\deg(E). \end{equation}

On the other hand, Lemma 3.4 implies

(3.8)\begin{equation} - \langle{E\vert E} \rangle = -\deg(E) ^2\langle{e\vert e} \rangle \geq \frac{\langle m_f\vert m_f\rangle}{1-\langle m_f\vert m_f\rangle}\deg(E)^2. \end{equation}

Putting these two inequalities together we get

(3.9)\begin{equation} \deg(E)^2 \leq\frac{1- \langle m_f\vert m_f\rangle}{\langle m_f\vert m_f\rangle} ( 2+ c_X \deg(E)). \end{equation}

Solving for the corresponding quadratic equation in $\deg (E)$, and applying the inequality $t(1-t)\leq 1/4$ with $t= \langle m_f\vert m_f\rangle$ finally gives

(3.10)\begin{equation} \langle m_f\vert m_f\rangle \deg(E) \leq (1-\langle m_f\vert m_f\rangle)c_X + 1/ \sqrt{2} \leq c_X+1. \end{equation}

For the second assertion, write $E$ as a union of disjoint connected components $E_i$. The classes $[E_i]$ are pairwise orthogonal, and are contained in $(\theta ^+_f)^\perp \cap (\theta ^-_f)^\perp$, a subspace of codimension $2$ in the Néron–Severi group of $X$. This implies that there are at most $\rho (X)-2$ connected components.

Proposition 3.7 Let $X$ be a compact Kähler surface with a reference Kähler form $\kappa _0$ such that $\int \kappa _0^2=1$. If $f\in \mathsf {Aut}(X)$ is loxodromic and $E$ is an $f$-invariant curve, then

\[ \deg(E)\leq 2^{54}(\rho(X)-2)(1+c_X) \deg(f)^{56}, \]

where the degrees are relative to $\kappa _0$ and $c_X$ is as in Lemma 3.5.

Proof. As in Remark 3.2, denote by $\operatorname {d}_{\mathbb {H}}$ the hyperbolic distance on $\mathbb {H}_X$ and let $\mathsf {Ax}(f)$ be the axis of the loxodromic isometry $f^*$. Lemma 4.8 in [BC16] implies that⁴

\[ \operatorname{d}_{\mathbb{H}}([\kappa_0], \mathsf{Ax}(f))\leq 28 \operatorname{d}_{\mathbb{H}} ([\kappa_0], f^*[\kappa_0]) = 28 \cosh^{-1}(\deg(f)). \]

Then, using the formula (3.4) for the distance $\operatorname {d}_{\mathbb {H}}([\kappa _0], \mathsf {Ax}(f))$ together with the elementary inequality $\cosh (kx)\leq 2^{k-1} \cosh (x)^k$, we obtain

(3.11)\begin{equation} \frac2{\langle \theta_f^+\vert \theta_f^-\rangle} = \cosh (\operatorname{d}_{\mathbb{H}}([\kappa_0], \mathsf{Ax}(f)))^2\leq 2^{54} (\deg(f))^{56}. \end{equation}

The result now follows from Lemma 3.5.

3.3 $\Gamma$-periodic curves, singular models, and ampleness

Denote by $\Pi _\Gamma ^\perp$ the orthogonal complement of $\Pi _\Gamma$ with respect to the intersection form.

Lemma 3.8 Let $\Gamma \subset \mathsf {Aut}(X)$ be a non-elementary subgroup.

1. (i) A curve $C\subset X$ is $\Gamma$-periodic if and only if $[C]\in \Pi _\Gamma ^\perp$.

2. (ii) If $\Gamma$ contains a parabolic element, and $C$ is irreducible, then $C$ is $\Gamma$-periodic if and only if $C$ is contained in a fiber of $\pi _g$ for every $g\in \Gamma _{\mathrm {par}}$.

Proof. For assertion (i), we note that since the intersection form is negative definite on $\Pi _\Gamma ^\perp$, $\Gamma$ acts on this space as a group of Euclidean isometries. Thus, if $c\in \Pi _\Gamma ^\perp$ is an integral class, then $\Gamma ^*(c)$ is a finite set. Since $\Pi _\Gamma$ is generated by nef classes, $[C]$ belongs to $\Pi _\Gamma ^\perp$ if and only if each of its irreducible components does, so it is enough to prove the result for an irreducible curve. Now an irreducible curve $C$ with negative self-intersection is uniquely determined by its class $[C]$; so if $[C]$ is contained in $\Pi _\Gamma ^\perp$, we conclude that $C$ is $\Gamma$-periodic. Conversely, if $C$ is $\Gamma$-periodic, a finite index subgroup $\Gamma '\subset \Gamma$ preserves $C$. If $f\in \Gamma '_{\mathrm {lox}}$, then $\langle \theta ^+_f \,\vert \, [C]\rangle =0$ because $f$ preserves the intersection form. But ${\mathrm {Vect}}( \theta ^+_f , f\in \Gamma '_{\mathrm {lox}})$ is a $\Gamma '$-invariant subspace of $\Pi _\Gamma$, hence by strong irreducibility it coincides with $\Pi _\Gamma$ (see § 3.1.3). Thus, $[C]\in \Pi _\Gamma ^\perp$, and in particular $[C]^2 <0$.

Let us prove the second assertion. If $[C]\in \Pi _\Gamma ^\perp$ and $g\in \Gamma _{\mathrm {par}}$, $[C]$ intersects trivially the class $[F]$ of the general fiber of $\pi _g$; this implies that $C$ is contained in a fiber of $\pi _g$, and is an irreducible component of a singular fiber since $[C]^2<0$. Now, denote by $S$ the set of irreducible curves which are contained in some fiber of $\pi _g$ for all $g\in \Gamma _{\mathrm {par}}$; it remains to prove that each $C\in S$ is $\Gamma$-periodic. Since $\Gamma$ is non-elementary, $\Gamma _{\mathrm {par}}$ contains two elements $g_1$ and $g_2$ with distinct fixed points on the boundary of $\mathbb {H}_X$; these fixed points are given by the classes $[F_1]$ and $[F_2]$ of any smooth fiber of $\pi _{g_1}$ and $\pi _{g_2}$, respectively; hence, $\pi _{g_1}$ and $\pi _{g_2}$ cannot share any smooth fiber. This shows that elements of $S$ are contained in singular fibers of $\pi _{g_1}$ and, in particular, $S$ is finite. Moreover, $S$ is $\Gamma$-invariant, because $\Gamma _{\mathrm {par}}$ is invariant under conjugacy, thus every $C\in S$ is a $\Gamma$-periodic curve.

Proposition 3.9 Let $\Gamma \subset \mathsf {Aut}(X)$ be a non-elementary subgroup containing parabolic automorphisms. There is a birational morphism $\pi _0\colon X\to X_0$ onto a normal projective surface $X_0$ and a homomorphism $\tau \colon \Gamma \to \mathsf {Aut}(X_0)$ such that:

1. (1) $\pi _0$ contracts all $\Gamma$-periodic curves and only them;

2. (2) $\pi _0$ is $\tau$-equivariant, that is, $\pi _0\circ f= \tau (f)\circ \pi _0$ for every $f\in \Gamma$;

3. (3) there is an ample line bundle $A$ on $X_0$ such that $\pi _0^*A$ is a big and nef line bundle, whose class belongs to $\Pi _\Gamma$.

This proposition shows that examples as in [CD20, § 11] do not appear for non-elementary groups containing parabolic automorphisms. Before starting the proof, recall that a line bundle $M$ on $X$ is semi-ample if and only if $mM$ is globally generated (or equivalently base-point free) for some $m>0$ (see [Laz04, § 2.1.B]); here we use the additive notation $mM$ for the line bundle $M^{\otimes m}$. If $M$ is semi-ample and $m\geq 1$ is sufficiently divisible, the line bundle $mM$ determines a morphism

(3.12)\begin{equation} \Phi_{mM}\colon X\to X_{mM} \subset \mathbb{P}(H^0(X,mM)^{\vee}), \end{equation}

onto a projective (possibly singular) normal variety $X_{mM}$. According to Theorem 2.1.27 in [Laz04], there is an algebraic fibre space $\Phi \colon X\to Y$ such that:

1. (1) $Y$ is a normal projective variety (see Example 2.1.15 in [Laz04]);

2. (2) $X_{mM}=Y$ and $\Phi _{mM}=\Phi$ for sufficiently divisible integers $m\geq 1$;

3. (3) there is an ample line bundle $A$ on $Y$ such that $\Phi ^*A=\ell M$ (for some $\ell \geq 1$).

Example 3.10 To each $g\in \mathsf {Aut}(X)_{\mathrm {par}}$ corresponds a semi-ample line bundle $L_g$ such that (i) the members of $\vert L_g\vert$ are given by the fibers of $\pi _g$ and (ii) $\pi _g\colon X\to B_g$ coincides with the fibration $\Phi \colon X\to Y$ determined by $L_g$. The ray $\mathbf {R}_+[L_g]\subset H^{1,1}(X;\mathbf {R})$ determines the unique fixed point of $g^*$ in $\partial \mathbb {H}_X$, and $L_g$ is nef (see § 3.1).

Proof of Proposition 3.9 By Lemma 3.8, we can fix a finite number of parabolic elements $g_i\in \Gamma$, with $1\leq i\leq k$ for some $k\geq 2$, such that the set of irreducible and $\Gamma$-periodic curves $C\subset X$ is exactly the set of irreducible curves which are contained in fibers of $\pi _{g_i}$ for $i= 1, \ldots, k$. The line bundle $M=\sum _i L_{g_i}$ is semi-ample, because the $L_{g_i}$ are; it is big because $M^2 >0$; and its class belongs to $\Pi _\Gamma$ because the classes $[L_{g_i}]$ belong to the limit set of $\Gamma$ (see [CD23c, § 2.3.6]). Since $M$ is big, the fibration $\Phi = \Phi _{mM}\colon X\to Y$ defined, as above, by some sufficiently divisible multiple of $M$, is a birational morphism (a generically finite fibration is a birational morphism since its fibers are, by definition, connected). By construction $\Phi$ contracts exactly the periodic curves of $\Gamma$. Thus, setting $\pi _0=\Phi$ and $X_0=Y$, we obtain a birational morphism that contracts all periodic curves, and only them. Since $\Gamma$ permutes these curves, it induces a group of automorphisms on $X_0$. Moreover, we know that there is an ample line bundle $A$ on $X_0$ such that $\pi _0^*A=\ell M$ for some $\ell \geq 1$; this proves the third assertion.

Remark 3.11 In the proof of Proposition 3.9, one may add extra parabolic automorphisms $g_j\in \Gamma _{\mathrm {par}}$, say with $k+1\leq j\leq \ell$, and replace $M$ by $\sum _{i=1}^\ell m_i L_i$ for any choice of integers $m_i>0$, while getting the same conclusion. After multiplication by $\mathbf {Q}_+^*$, the classes constructed in this way form a dense subset of the convex cone

(3.13)\begin{equation} \bigg\{\sum_{i=1}^\ell \alpha_i c_1(L_{g_i}); \ell \geq 1,\ g_i\in \Gamma_{\mathrm{par}},\ {\text{and}}\ \alpha_i \in \mathbf{R}_+^*\ {\text{for all}}\ i\bigg\}. \end{equation}

This cone is $\Gamma$-invariant, its closure is the smallest convex cone whose projectivization contains the limit set $\operatorname {Lim}(\Gamma )$, and it spans $\Pi _\Gamma$ because $\Pi _\Gamma$ is the smallest vector space containing $\operatorname {Lim}(\Gamma )$. Thus, the classes of the form $\alpha c_1(\pi _0^*A)$, where $A$ runs over the set of ample line bundles on $X_0$ and $\alpha$ runs over $\mathbf {Q}_+^*$, is a dense subset of this cone.

3.4 Proof of Theorem D

Let us first deal with the case where $\Gamma$ is elementary. By [Can14, Theorem 3.2] there is a loxodromic element $f\in \Gamma$ such that $(f^*)^\mathbf {Z}$ has finite index in $\Gamma ^*$. If $\mathsf {Aut}(X)^0$ is non-trivial, then $X$ is a torus and then $f$ has no invariant curve (see [Can14, Remark 3.3] and [CF03]). Otherwise, the kernel of the homomorphism $\Gamma \to \Gamma ^*$ is finite, $f^\mathbf {Z}$ has finite index in $\Gamma$, and therefore a curve is $\Gamma$-periodic if and only if it is $f$-periodic, so we are done when $\Gamma$ is elementary.

When $\Gamma$ is non-elementary, Theorem D is covered by the following more precise statement (recall that $X$ is automatically projective in this case [CD23a]).

Proposition 3.12 Let $X$ be a complex projective surface and $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(X)$. Then there exists a loxodromic element $f$ in $\Gamma$ such that every $f$-periodic curve is $\Gamma$-periodic.

If, in addition, $\Gamma$ contains a parabolic element $g$, then $f$ can be chosen of the form $f=h^N \circ g^N$ for some $h$ which is conjugate to $g$ in $\Gamma$ and $N$ is any sufficiently large integer. If, moreover, $N$ is sufficiently divisible, then $(g^N)^*$ is unipotent.

Proof. Consider a subset $S\subset \Gamma _{\mathrm {lox}}$ such that $\{ (\mathbb {P}(\theta ^+_f), \mathbb {P}(\theta ^-_f));\ f\in S \}$ is dense in $\operatorname {Lim}(\Gamma )^2$, as in Lemma 3.3. Let us exhibit an $f\in S$ such that every $f$-periodic curve is $\Gamma$-periodic. By contradiction, we assume that every $f\in S$ admits at least one irreducible periodic curve $C(f)$ which is not $\Gamma$-periodic, and we set $c(f)=[C(f)]$. By Lemma 3.8, $c(f)$ does not belong to $\Pi _\Gamma ^\perp$, thus $u\mapsto \langle c(f)\vert u\rangle$ is a non-trivial linear form on $\Pi _\Gamma$. Since the class of any periodic curve is orthogonal to $\Pi _f$, $\langle c(f)\vert \theta ^+_f\rangle = \langle c(f)\vert \theta ^-_f \rangle = 0$.

Let $U$ and $U'$ be open subsets of $\partial \mathbb {H}_X$ intersecting $\operatorname {Lim}(\Gamma )$ non-trivially, and such that $\overline U\cap \overline U' = \emptyset$; let $x$ be an element of $U\cap \operatorname {Lim}(\Gamma )$. Define

(3.14)\begin{equation} A(U,U')=\{ f\in \mathsf{Aut}(X);\ f\ {\text{is loxodromic}},\ \mathbb{P}(\theta^+_f)\in U \ {\text{and}}\ \mathbb{P}(\theta^-_f)\in U'\}, \end{equation}

and

(3.15)\begin{equation} D(U,U')=\{ c(f);\ f \in A(U,U')\cap S\}. \end{equation}

By Lemma 3.5, $D(U,U')$ is a finite set. From our assumption on $S$, there is a sequence $(f_n)$ of elements in $A(U,U')\cap S$ such that $x=\lim _n(\mathbb {P}(\theta ^+_{f_n}))$. Extracting a subsequence if necessary we may assume that $c(f_n)$ is constant, equal to some $c_\infty \in D(U,U')$, and we infer that $x$ is contained in $c_\infty ^\perp$. As a consequence, the limit set $\operatorname {Lim}(\Gamma )\subset \mathbb {P}(\Pi _\Gamma )$ is locally contained in the finite union of hyperplanes $\mathbb {P}(c^\perp \cap \Pi _\Gamma )$, for $c\in D(U,U')$. By compactness, $\operatorname {Lim}(\Gamma )$ is contained in a finite union of hyperplanes, which contradicts the strong irreducibility of the action of $\Gamma$ on $\Pi _\Gamma$.

Now, to prove the first assertion of the proposition, we simply put $S = \Gamma _{\mathrm {lox}}$; by Lemma 3.3, it satisfies the desired density property.

For the second assertion, we remark that the set of fixed points $(u,u')$ of all pairs $(h,h')$, where $h$ and $h'$ run independently over the conjugacy class of $g$, is dense in $\operatorname {Lim}(\Gamma )^2$. If we apply Lemma 3.13 we see that the set of all loxodromic elements $f=h^N\circ (h')^N$ with $h$ and $h'$ conjugate to $g$ satisfies the desired density property. The property ‘any irreducible $f$-periodic curve is also $\Gamma$-periodic’ being invariant under conjugacy, we can choose $f=h^N\circ g^N$ for some conjugate $h$ of $g$ and any large enough $N$.

The last assertion follows from Lemma 3.1.

Lemma 3.13 Let $h$ and $h'$ be two parabolic elements of $\mathsf {Aut}(X)$ with distinct fixed points $u$ and $u'$ in $\partial \mathbb {H}_X$. Let $U$ and $U'$ be small, disjoint neighborhoods of $u$ and $u'$, respectively, in $\mathbb {P}(\Pi _\Gamma )$. Then if $N\in \mathbf {Z}$ is large enough, $f_N:=h^N\circ (h')^N$ is a loxodromic automorphism such that $\mathbb {P}(\theta ^+_{f_N})\in U$ and $\mathbb {P}(\theta ^-_{f_N})\in U'$.

Proof. Let us denote by $\mathbb {P}(h^*)$ the linear projective transformation induced by $h^*$ on $\mathbb {P}({\mathrm {NS}}(X;\mathbf {R}))$. Since $U$ does not contain $u'$, $\mathbb {P} (h'^*)^N(U)\subset U'$ if $\vert N\vert$ is large enough; similarly $\mathbb {P} (h^*)^N(U')\subset U$. So for $f_N=h^N\circ (h')^N$, $\mathbb {P} (f_N^*)$ maps $U'$ strictly inside itself and likewise $\mathbb {P} ((f_N^{-1})^*)$ maps $U$ strictly inside itself. This implies that $f_N$ is loxodromic, with its $\alpha$-limit and $\omega$-limit points in $U'$ and $U$, respectively.

4. Complex tori and Kummer examples

This section gathers some facts on automorphism groups of complex tori. We also introduce and study the notion of a Kummer group. Part of this material is well known, we provide the details for completeness.

4.1 Finite orbits on tori

Consider a compact complex torus $A=\mathbf {C}^k/\Lambda$. Each automorphism $f$ of $A$ is an affine transformation $f(z)=L_f(z)+t_f$, where $z\mapsto z+t_f$ is the translation part and $L_f$ is a linear automorphism, induced by a linear transformation of $\mathbf {C}^k$ that preserves $\Lambda$. Let $\Gamma$ be a subgroup of $\mathsf {Aut}(A)$.

Warning. By definition, compact tori and abelian varieties come equipped with their group structure, in particular with their neutral element, or ‘origin’. On the other hand, an automorphism $f$ with a non-trivial translation part $t_f$ does not preserve this group structure. If $x\in A$ is fixed by $\Gamma$, conjugating $\Gamma$ by the translation $z\mapsto z+x$ we may assume that $\Gamma$ fixes the origin of $A$ and acts by linear isomorphisms. Alternatively, we can transport the group structure by this translation and put the origin at $x$: this changes the group structure but not the underlying complex manifold. We shall frequently do this operation without always specifying the change in the group structure of $A$.

Suppose the orbit $\Gamma (x)\subset A$ is finite, of cardinality $m$, and consider the stabilizer $\Gamma _0\subset \Gamma$ of $x$; its index divides $m !$. Conjugating $\Gamma$ by $z\mapsto z+x$, as explained above, all elements $f\in \Gamma _0$ are linear. In that case, every torsion point has a finite $\Gamma _0$-orbit, hence also a finite $\Gamma$-orbit; in particular, finite orbits of $\Gamma$ form a dense subset of $A$ for the Euclidean topology. The next proposition summarizes this discussion.

Proposition 4.1 Let $A$ be a compact complex torus, and let $\Gamma$ be a subgroup of $\mathsf {Aut}(A)$. If  $\Gamma$ has a finite orbit, then its finite orbits form a dense subset of $A$. More precisely, if a periodic point of $\Gamma$ is chosen as the origin of $A$ for its group law, then all torsion points of $A$ are periodic points of $\Gamma$.

Remark 4.2 If in Proposition 4.1 we moreover assume that $\dim _\mathbf {C} A=2$ and $\Gamma$ contains a loxodromic element fixing the origin, then conversely all periodic points of $\Gamma$ are torsion points. This follows from Lemma 4.3.

4.2 Dimension 2

Let $A=\mathbf {C}^2/\Lambda$ be a compact complex torus of dimension $2$, and let $f(z)=L_f(z)+t_f$ be a loxodromic element of $\mathsf {Aut}(A)$. The loxodromy means exactly that the eigenvalues $\alpha$ and $\beta$ of $L_f$ satisfy $\vert \alpha \vert <1<\vert \beta \vert$. Pick a basis of $\Lambda$, and use it to identify $\Lambda$ with $\mathbf {Z}^4$ and $\mathbf {C}^2$ with $\mathbf {R}^4$, as real vector spaces. Then, $L_f$ corresponds to an element $M_f\in {\sf {GL}}_4(\mathbf {Z})$.

Lemma 4.3 Let $f$ be a loxodromic automorphism of a compact complex torus $A$ of dimension $2$. Then:

1. (1) $f$ has a fixed point, and after translation $z\mapsto z+x$ by such a fixed point, its periodic points are exactly the torsion points of $A$;

2. (2) there is no $f$-invariant curve: the orbit $f^\mathbf {Z}(C)$ of any curve is dense in $A$.

Proof. With the above notation, the fixed points of $f$ are determined by the equation $(L_f-{\rm id})(z)\in \Lambda -t_f$ or, equivalently, $(M_f-{\rm id})(z)\in \mathbf {Z}^4-t_f$. The complex eigenvalues of $L_f$ being $\neq 1$, there is at least one fixed point. Thus, after conjugation by a translation, we may assume that $t_f=0$. Then, the periodic points of $f$ correspond to the points $x\in \mathbf {R}^4$ such that $M_f^n (x)-x \in \mathbf {Z}^4$; any solution to such an equation being rational, it corresponds to a torsion point in $A$. This proves property (1). For property (2), we may now assume that $t_f=0$. There are two linear forms $\xi _f^+$, $\xi _f^-\colon \mathbf {C}^2\to \mathbf {C}$ such that $\xi _f^+\circ L_f=\alpha \xi _f^+$ and $\xi _f^-\circ L_f=\beta \xi _f^-$. They determine two linear foliations on $A$: the stable and unstable foliations of $f$. Both have dense leaves. If $y$ is a torsion point, $y$ is $f$-periodic, and its stable manifold, being dense, intersects $C$. Thus, the sequence $(f^n(C))$ accumulates at every torsion point, so it is dense in $A$, and $C$ is not invariant.

4.3 Kummer structures

4.3.1 Kummer groups

Let $X$ be a compact Kähler surface, and let $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$. By definition $(X, \Gamma )$ is a Kummer group if there is a (compact) torus $A$, a finite subgroup $G$ of $\mathsf {Aut}(A)$, a subgroup $\Gamma _A$ of $\mathsf {Aut}(A)$ containing $G$, and a bimeromorphic morphism $q_X\colon X\to A/G$ such that the following hold.

1. (a) $\Gamma _A$ normalizes $G$. Thus, if $q_A\colon A\to A/G$ is the quotient map, there is a homomorphism $h\in \Gamma _A \mapsto \overline {h} \in \mathsf {Aut}(A/G)$ such that $q_A\circ h=\overline {h}\circ q_A$ for every $h\in \Gamma _A$; we shall denote by $\overline \Gamma _A$ the image of this homomorphism.

2. (b) The bimeromorphic map $q_X\!\!$ is $\Gamma$-equivariant: there is a homomorphism $\Gamma \ni f \mapsto \overline f \in \mathsf {Aut}(A/G)$, whose image is denoted by $\overline \Gamma$, such that $q_X\circ f=\overline f \circ q_X$ for every $f\in \Gamma$.

3. (c) The subgroups $\overline \Gamma$ and ${\overline {\Gamma }}_A$ of $\mathsf {Aut}(A/G)$ coincide.

To each $f\in \Gamma$ corresponds an element $f_A\in \Gamma _A$, unique up to composition with elements of $G$; the type of $f$ as an automorphism of $\mathsf {Aut}(X)$ coincides with the type of $f_A$ as an automorphism of $A$, and $\lambda (f)=\lambda (f_A)$. When $X$ is projective, $A$ is an abelian surface and $q$ is a birational morphism. According to the usual terminology, we also say that $f\in \mathsf {Aut}(X)$ is a Kummer example when $(X, f^\mathbf {Z})$ is a Kummer group.

Remark 4.4 Consider a section $\Omega _A$ of the canonical bundle $K_A$ such that $\int _A\Omega _A\wedge {\overline {\Omega _A}}=1$; it is unique up to multiplication by a complex number of modulus one. In particular, the volume form ${\sf {vol}}_A=\Omega _A\wedge {\overline {\Omega _A}}$ is invariant under $\mathsf {Aut}(A)$. The quotient of ${\sf {vol}}_A$ by the action of $G$ determines a probability measure on $A/G$, and then on $X$. This probability measure coincides with the measure of maximal entropy $\mu _f$ for every $f\in \Gamma _{\mathrm {lox}}$.

From the definition of a Kummer group, Proposition 4.1 and Remark 4.2 we obtain the following.

Proposition 4.5 Let $(X, \Gamma )$ be a Kummer group with at least one finite orbit. Then, its finite orbits are dense in $X$ for the euclidean topology, and there is a dense, $\Gamma$-invariant, Zariski-open subset in which all periodic points of loxodromic elements of $\Gamma$ coincide.

4.3.2 Classification of Kummer examples

Let us consider, first, the case of an infinite cyclic group generated by a loxodromic Kummer example $f$. From the classification given in [CF03, CF05], we may assume that the finite group $G$ is a cyclic group fixing the origin of $A$; in other words, $G$ is induced by a cyclic subgroup of ${\sf {GL}}_2(\mathbf {C})$ preserving the lattice $\Lambda$ such that $A=\mathbf {C}^2/\Lambda$. There are only seven possibilities:

1. (1) $G=\{ {\rm id}\}$ and $X$ is a blow-up of a torus $A$;

2. (2) $G=\{{\rm id}, -{\rm id}\}$ and $A/G$ is a Kummer surface, in the classical sense; in particular, $X$ is a blow-up of a K3 surface;

3. (3) $A$ is the torus $(\mathbf {C}/\mathbf {Z}[{\mathsf {i}}])^2$ and $G$ is the group of order $4$ generated by ${\mathsf {i}} {\rm id}$; in this case $X$ is a rational surface;

4. (4) $A$ is the torus $(\mathbf {C}/\mathbf {Z}[\exp (2{\mathsf {i}} \pi /3)])^2$ and $G$ is the group of order $3$ generated by $\exp (2{\mathsf {i}} \pi /3) {\rm id}$; in this case $X$ is a rational surface;

5. (5) $A$ is the torus $(\mathbf {C}/\mathbf {Z}[\exp (2{\mathsf {i}} \pi /3)])^2$ and $G$ is the group of order $6$ generated by $\exp ({\mathsf {i}} \pi /3) {\rm id}$; in this case $X$ is a rational surface;

6. (6) let $\zeta _5$ be a primitive fifth root of unity; the cyclotomic field $\mathbf {Q}[\zeta _5]$ has two distinct non-conjugate embeddings in $\mathbf {C}$, $\sigma _1$ and $\sigma _2$, determined by $\sigma _1(\zeta _5)=\zeta _5$ and $\sigma _2(\zeta _5)=\zeta _5^2$; the ring of integers coincides with $\mathbf {Z}[\zeta _5]$ and its image by $\sigma =(\sigma _1,\sigma _2)$ is a lattice $\Lambda _5\subset \mathbf {C}\oplus \mathbf {C}$; the abelian surface $A$ is the quotient $\mathbf {C}^2/\Lambda _5$; the group $G$ is generated by the diagonal linear map $(x,y)\mapsto (\zeta _5 x, \zeta _5^2 y)$ and has order $5$; here, $X$ is rational too;

7. (7) as in the previous example, $A=\mathbf {C}^2/\Lambda _5$, but now $G$ has order $10$ and is generated by $(x,y)\mapsto (-\zeta _5 x, \zeta _5 y)$, and again $X$ is rational.

These constraints on $(A,G)$ apply to non-elementary Kummer groups; in particular, we shall always assume that $G$ is cyclic and fixes the neutral element of $A$. In cases (1)–(5) of the above list, the abelian surface is $\mathbf {C}^2/(\Lambda _0\times \Lambda _0)$ for some lattice $\Lambda _0$ in $\mathbf {C}$. The natural action of ${\sf {GL}}(2, \mathbf {Z})$ on $\mathbf {C}^2$ preserves $\Lambda _0\times \Lambda _0$, and induces a non-elementary subgroup of $\mathsf {Aut}(A)$, which commutes to $G$; hence, it determines also a non-elementary subgroup of $\mathsf {Aut}(A/G)$. On the other hand, cases (6) and (7) do not appear.

Lemma 4.6 If $(X, \Gamma )$ is a non-elementary Kummer group, then $G$ is generated by a homothety and the quotient $A/G$ is not of type (6) or (7) in the classification above.

Proof. The group $\Gamma _A$ permutes the fixed points of $G$. Thus, the stabilizer $\Gamma _A^\circ ={\mathrm {Stab}}_{\Gamma _A}(0)$ of the neutral element is a finite index, non-elementary subgroup of $\Gamma _A$. Pick any loxodromic element $f$ in $\Gamma _A^\circ$; it acts by conjugacy on $G$, which is finite, so there is a positive iterate such that $f^n\circ g=g\circ f^n$ for all $g\in G$. Near the origin, $f^n$ and $g$ are two commuting linear transformations, $f^n$ has two eigenvalues, of modulus $<1$ and $>1$, respectively, and $g$ must preserve the corresponding stable and unstable directions of $f$. Since $\Gamma _A^\circ$ is non-elementary, these tangent directions form an infinite set as $f$ varies in the set of loxodromic elements of $\Gamma _A^\circ$, so $g$ is a homothety, and we are done.

4.3.3 Invariant curves

We keep the notation from the previous paragraphs and consider a non-elementary Kummer group $(X, \Gamma )$. The singularities of $A/G$ are cyclic quotient singularities and $X$ dominates a minimal resolution of $A/G$.

Let us examine case (2), when $G=\{ {\rm id}, -{\rm id}\}$. Then $G$ has $16$ fixed points, and to resolve the $16$ singularities of $A/G$ one can proceed as follows. First, one blows up the fixed points, creating $16$ rational curves. Then one lifts the action of $G$ to the blow-up $\hat {A}$. If $E$ is one of the exceptional divisors, then $G$ fixes $E$ pointwise and acts as $w\mapsto -w$ transversally, so locally the quotient map can be written $(w,z)\mapsto (w^2,z)$, with $E=\{ w=0\}$ giving rise to a smooth rational curve of self-intersection $-2$ on $\hat {A}/G$. This construction provides the minimal resolution $X_{\mathrm {min}}=\hat {A}/G$ of $A/G$, the singularities being replaced by disjoint $(-2)$-curves. Cases (3), (4), and (5) can be handled with a similar process because if $x\in A$ is stabilized by a subgroup $H$ of $G$, then $H$ is locally given around $x$ as a cyclic group of homotheties; so, in the minimal resolution of $A/G$ the singularities are replaced by disjoint rational curves $E_i$ of negative self-intersection $E_i^2\in \{-2, \ldots, -6\}$. Cases (6) and (7) are more delicate; however, by Lemma 4.6, we do not need to deal with them.

Lemma 4.7 Let $(X, \Gamma )$ be a non-elementary Kummer group on a smooth projective surface. Then:

1. (1) $X$ is an abelian surface if and only if $\Gamma$ admits no invariant curve;

2. (2) any connected $\Gamma$-periodic curve $D$ is a smooth rational curve, and the induced dynamics of $\mathrm {Stab}_D(\Gamma )$ on $D$ has no periodic orbit.

Moreover, $D_f=D_\Gamma$ for every $f\in \Gamma _{\mathrm {lox}}$.

Proof. The minimal resolution $X_{\rm min}$ of $A/G$ is unique, up to isomorphism (see [BHPV04, § III.6], Theorems (6.1) and (6.2), and their proofs). Thus, $X$ dominates $X_{\rm min}$ and every $f\in \Gamma$ preserves the exceptional divisor of the morphism $X\to X_{\rm min}$ and induces an automorphism $f_{\rm min}$ of $X_{\rm min}$. In particular, $\Gamma$ admits an invariant curve, unless $G=\{ \mathrm {id} \}$ and $X=X_{\rm min} = A$. Conversely, in that case $\Gamma$ has no invariant curve, by Lemma 4.3. This proves the first assertion.

Let us prove the second assertion for the induced group $\Gamma _{\rm min}\subset \mathsf {Aut}(X_{\mathrm {min}})$. Let $E$ be a connected periodic curve for $\Gamma _{\rm min}$. If $f_{\rm min}\in \Gamma _{\rm min}$ is loxodromic, it comes from an Anosov map $f_A\colon A\to A$, as in Lemma 4.3, and $f_A$ does not have any periodic curve. Since $E$ is $f_{\rm min}$-periodic, it is contained in the exceptional divisor of the resolution $X_{\rm min}\to A/G$; as explained before the lemma, this divisor is a disjoint union of rational curves, so $E$ is one of these rational curves $E_x = q_{X_{\mathrm {min}}}^{-1}(q_A(x))$, where $x\in A$ has a non-trivial stabilizer $G_x\subset G$. In particular $x$ is fixed by a finite index subgroup $\Gamma _{A,x}$ of $\Gamma _A$. Now since $\Gamma$ is non-elementary, $\Gamma _A$ and $\Gamma _{A,x}$ are non-elementary as well, and since the action of $\Gamma _{A,x}$ on $A$ is by affine transformations, its action on the exceptional divisor $E_x$ is that of a non-elementary subgroup of ${\sf {PGL}}_2(\mathbf {C})=\mathsf {Aut}(E_x)$. In particular, $\Gamma _{A,x}$ does not admit any finite orbit in $E_x$.

The birational morphism $\pi : X\to X_{\mathrm {min}}$ is equivariant with respect to $\Gamma$ and its image $\Gamma _{\mathrm {min}}$ in $\mathsf {Aut}(X_{\mathrm {min}})$. Thus, $\pi ^{-1}$ blows up periodic orbits of $\Gamma _{\mathrm {min}}$. The last few lines show that, when such a periodic point $y\in X_{\mathrm {min}}$ is blown up, first $y$ does not lie on the exceptional locus of $X_{\mathrm {min}}\to A/G$ and, second, the exceptional divisor $E_y$ does not contain any finite orbit. Thus, $X$ is obtained by simple blow-ups centered on a finite set of distinct periodic points of $\Gamma _{\rm min}$, every connected component of the exceptional locus of $q_X$ is a smooth rational curve, and there is no $\Gamma$-periodic point in these curves.

5. Unlikely intersections for non-elementary groups

This section is devoted to the proof of Theorem B.

5.1 Strategy of the proof

If $\Gamma$ has a Zariski-dense set $F$ of finite orbits, a standard argument shows that there is a sequence $(x_n)\in F^\mathbf {N}$ which is generic (given any fixed proper subvariety $Y\subset X$, $x_n\notin Y$ for $n$ large enough). Let $m_{x_n}$ be the probability measure equidistributed over the Galois orbit of $x_n$. We want to use arithmetic equidistribution to show that the sequence of measures $(m_{x_n})$ converges when $n\to \infty$. For this, we need a height function $h_L$ (associated to some line bundle $L$ on $X$ with appropriate positivity properties) that vanishes on $F$. In §§ 5.2–5.4 we construct such height functions: they are associated to the choice of certain finitely supported probability measures $\nu$ on $\Gamma$. Indeed, to such a measure we associate the linear endomorphism $P_\nu ^*=\sum \nu (f) f^*$ of the Néron–Severi group ${\mathrm {NS}}(X;\mathbf {R})$, and we construct a big and nef line bundle $L$, that depends on $\nu$, such that $P_\nu ^*[L]=\alpha (\nu )[L]$ for some $\alpha (\nu )>1$; then, $h_{L}$ will be a Weil height that satisfies the invariance $\sum \nu (f)h_L\circ f = \alpha (\nu ) h_L$. The arithmetic equidistribution theorem of Yuan shows that the measures $m_{x_n}$ converge to a measure $\mu _\nu =S\wedge S$, where $S$ is a dynamically defined closed positive current with cohomology class equal to $[L]$. On the other hand, the measures $m_{x_n}$, hence their limit $\mu :=\mu _\nu$, do not depend on $\nu$. As we vary the choice of $\nu$, the construction has enough flexibility to show that for every $f\in \Gamma _{\mathrm {lox}}$, $\mu _\nu$ can be made arbitrary close to the maximal entropy measure $\mu _f$. It follows that $\mu _f=\mu$ is independent of $f$ and is $\Gamma$-invariant. In § 5.5, the dynamics of parabolic elements of $\Gamma$ is used to deduce that $\operatorname {Supp}(\mu ) = X$. Then the classification of $\Gamma$-invariant measures from [Can01b, CD23b] implies that $\mu$ has a smooth density, and the main result of [CD20] shows that every $f\in \Gamma _{\mathrm {lox}}$ is a Kummer example (Theorem 5.17 in § 5.6). At this point the Kummer structure may a priori depend on $f$, as in Example 5.1 below. This issue is solved in § 5.7 by adding an argument based on Theorem D which finally shows that $(X, \Gamma )$ is a Kummer group.

Example 5.1 Let $X$ be a Kummer surface possessing both a Kummer automorphism $f$ and a non-Kummer one $h$, as in [KK01]. Then, $f$ and $h\circ f \circ h^{-1}$ are two Kummer automorphisms which are not associated with the same Kummer structure; the pair $(X, \langle f, h\circ f \circ h^{-1}\rangle )$ is not a Kummer group.

5.2 Kawaguchi's currents

5.2.1 Action on $H^{1,1}$

Let $X$ be a compact Kähler surface and let $\nu$ be a probability measure on $\mathsf {Aut}(X)$ satisfying the (exponential) moment assumption

(5.1)\begin{equation} \int ({\Vert f \Vert}_{C^1} + {\Vert f^{-1} \Vert}_{C^1})^2\, d\nu(f) <+\infty. \end{equation}

By [CD23c, Lemma 5.1], this implies

(5.2)\begin{equation} \int {\Vert f^* \Vert} \,d\nu(f) <+\infty, \end{equation}

where $f^*$ is the endomorphism of $H^{2}(X;\mathbf {R})$ determined by $f$ and ${\Vert \cdot \Vert }$ is any operator norm. (For the proof of Theorem 5.17, we will only consider finitely supported measures so the moment conditions will be trivially satisfied.) Let $\Gamma _\nu$ be the subgroup of $\mathsf {Aut}(X)$ generated by the support of $\nu$. We let $P_\nu$ be the linear endomorphism of $H^{2}(X;\mathbf {C})$ defined for every $u\in H^{2}(X;\mathbf {C})$ by

(5.3)\begin{equation} P_\nu(u)=\int f^*(u)\,d\nu(f). \end{equation}

The following lemma is a strong version of the Perron–Frobenius theorem. Recall that the Kähler form $\kappa _0$ was fixed in § 3.

Lemma 5.2 Assume that $\Gamma _{\nu }$ is non-elementary. Then, $P_\nu$ has a unique eigenvector $w_\nu \in H^{1,1}(X;\mathbf {R})$ such that $w_\nu ^2=1$ and $\langle w_\nu \vert [\kappa _0]\rangle >0$. This eigenvector is big and nef. The eigenvalue $\alpha (\nu )$ such that

\[ P_\nu(w_\nu)= \alpha(\nu) w_\nu \]

is larger than $1$ and coincides with the spectral radius of $P_\nu$; the multiplicity of $\alpha (\nu )$ is equal to $1$, and all other eigenvalues $\beta \in \mathbf {C}$ of $P_\nu$ satisfy $\vert \beta \vert < \alpha (\nu )$.

Proof. Recall the definition of the open convex cone $\mathrm {Pos}(X)\subset H^{1,1}(X;\mathbf {R})$ from § 3.1. Since every $f\in \mathsf {Aut}(X)$ preserves $\mathrm {Pos}(X)$, $P_\nu$ preserves $\mathrm {Pos}(X)$ too, by convexity; moreover, if $u\in \partial \mathrm {Pos}(X)\setminus \{0\}$ and $u':=P_\nu (u)\in \partial \mathrm {Pos}(X)$, then $f^*(u)\in \mathbf {R}_+u'$ for all $f$ in $\operatorname {Supp}(\nu )$. Thus, we can apply the results of Vandergraft [Van68]. In his terminology, the faces of $\overline {\mathrm {Pos}}(X)$ are the isotropic rays in $\partial \mathrm {Pos}(X)$, so $P_\nu$ is irreducible, because if a face $\mathbf {R}_+ u$ were fixed by $P_\nu$ it would be fixed by every $f$ in $\operatorname {Supp}(\nu )$, and $\Gamma _\nu$ would be elementary. Thus, Theorems 4.2 and 4.3 of [Van68] imply that the spectral radius $\alpha (\nu )$ of $P_\nu$ is a simple eigenvalue of $P_\nu$ and the corresponding eigenline $\mathbf {R} w_\nu$ intersects $\mathrm {Pos}(X)$; choosing $w_\nu \in \mathbb {H}_X$, $w_\nu$ is uniquely determined.

If $w, w'\in \mathbb {H}_X$, then $\langle w \vert w'\rangle \geq 1$ with equality if and only if $w=w'$. Computing the self-intersection of $P_\nu (w_\nu )$, we deduce that $\alpha (\nu )\geq 1$. In addition, $\alpha (\nu )=1$ if and only if $f^*(w_\nu )=w_\nu$ for every $f$ in $\operatorname {Supp}(\nu )$, which would imply that $\Gamma _\nu$ is elementary; hence, $\alpha (\nu )>1$. The Kähler cone satisfies also $P_\nu ({\mathrm {Kah}}(X))\subset {\mathrm {Kah}}(X)$. Hence, $w_\nu$ is nef (it is in the closure of ${\mathrm {Kah}}(X)$). It is big because it is nef and has positive self-intersection (see, e.g., [Laz04, Theorem 2.2.16]).

Let us show that $\alpha (\nu )$ is greater in magnitude than any other eigenvalue of $P_\nu$; for this, we can of course replace $P_\nu$ by $P_\nu ^N$, for some $N\geq 1$ to be chosen below. According to [Van68, Theorem 4.4] it is sufficient to show that $P_\nu ^N(\overline { \mathrm {Pos}(X)})\subset {\mathrm {Pos}(X)}$. As said above, if this fails there exists $u, u'\in \partial \mathrm {Pos}(X)\setminus \{0\}$ such that $f^*u\in \mathbf {R} u'$ for every $f\in \operatorname {Supp}(\nu ^{\otimes N})$. On the other hand, for $N$ large, there exist three loxodromic elements $f_1, f_2, f_3\in \operatorname {Supp}(\nu ^{\otimes N})$ with disjoint fixed points (apply [BQ16, Theorem 6.36] and [CD23c, Proposition 2.8]). Replacing $N$ by $NN'$ and $f_i$ by $f_i^{N'}$ if necessary, we can further assume that there are six disjoint open sets $B_i^\pm$, $i=1,2,3$, in $\partial \mathbb {H}_X = \mathbb {P}( \partial \mathrm {Pos}(X)) \subset \mathbb {P}(H^{1,1}(X, \mathbf {R}))$ such that $\mathbb {P}(f_i)(\partial \mathbb {H}_X \setminus B_i^-)\subset B_i^+$ for every $i$. Now, suppose $u, u'\in \partial \mathrm {Pos}(X)\setminus \{0\}$ satisfy $f_i^*u\in \mathbf {R} u'$ for $i=1,2,3$. If $\mathbb {P}(u)$ is in none of the $B_i^-$, then $\mathbb {P}(u')$ must be in the intersection of the $B_i^+$, a contradiction. Otherwise, $\mathbb {P}(u)$ is in exactly one of the $B_i^-$, say $B_1^-$, and $\mathbb {P}(u')$ should be in $B_2^+\cap B_3^+$, a contradiction. Thus, we are done.

Example 5.3 (see [Can14, § 2] and [CD20, § 2.2])

Let $f$ be a loxodromic automorphism, and take $\nu$ to be the probability measure $p\delta _f+q\delta _{f^{-1}}$ with $p, q \geq 0$ and $p+q=1$. Note that $\Gamma _\nu =f^{\mathbf {Z}}$ does not satisfy the assumption of Lemma 5.2. Then $P_{\nu }=p f^*+q(f^{-1})^*$ preserves the $f^*$-invariant plane $\Pi _f\subset H^{1,1}(X;\mathbf {R})$. If $p> q$, the spectral radius of $P_{\nu }$ is equal to $p\lambda (f) + q/\lambda (f)$, and the corresponding eigenspace is the isotropic line of $\Pi _f$ corresponding to the eigenvalue $\lambda (f)$ of $f$; if $p< q$, the spectral radius is equal to $p/\lambda (f) + q\lambda (f)$ and the eigenspace is the other isotropic line in $\Pi _f$. If $p=q=1/2$, then $(P_\nu )_{\vert \Pi _f}$ is the scalar multiplication by

(5.4)\begin{equation} \alpha(f)=\tfrac{1}{2}(\lambda(f)+1/\lambda(f)), \end{equation}

$\alpha (f)>1$, and all vectors $u\in \Pi _f$ satisfy $P_\nu (u)=\alpha (f) u$. This example shows that the previous lemma fails for $\nu$, whatever the values of $p$ and $q$ are: the dominant eigenvector is at the boundary of the hyperbolic space, or is not unique.

5.2.2 Stationary currents

Let us borrow some notation from [CD23c, § 6.1]: we fix Kähler forms $\kappa _i$, whose cohomology classes provide a basis $([\kappa _i])$ of $H^{1,1}(X;\mathbf {R})$. Then, if $a$ is any element of $H^{1,1}(X;\mathbf {R})$, there is a unique $(1,1)$-form $\Theta (a)=\sum _i a_i \kappa _i$ in $\operatorname {Vect}(\kappa _i,\ 1\leq i\leq h^{1,1}(X))$ whose class $[\Theta (a)]$ is equal to $a$. If $S$ is any closed positive current of bidegree $(1,1)$, then $S=\Theta ([S])+dd^cu_S$ for some upper semi-continuous function $u_S\colon X\to \mathbf {R}$: this function is locally the difference of a plurisubharmonic (psh) function and a smooth function, and it is unique up to an additive constant.

The following proposition is essentially due to Kawaguchi, who proved it in [Kaw06] under slightly more restrictive assumptions.

Proposition 5.4 Let $X$ be a compact Kähler surface, and let ${\sf {vol}}$ be a smooth volume form on $X$. Let $\nu$ be a probability measure on $\mathsf {Aut}(X)$ satisfying the moment condition (5.1). Assume that we are in one of the following two situations:

1. (i) $\Gamma _\nu$ is non-elementary; in this case, set $w=w_\nu$, and $\alpha = \alpha (\nu )$, as in Lemma 5.2;

2. (ii) $\nu =\frac {1}{2}(\delta _f+\delta _{f^{-1}})$ for some loxodromic automorphism and $w$ is a fixed point of $ ({1}/{\alpha (f)})P_\nu$ in $\mathbb {H}_X$, as in Example 5.3; in this case, set $\alpha =\alpha (f)$.

Then, there is a unique closed positive current $S$ such that

(5.5)\begin{equation} \int f^*(S)\,d\nu(f)=\alpha S \quad{\text{and}} \quad [S]=w. \end{equation}

This current has continuous potentials: $S=\Theta (w)+dd^c(u)$ for a unique continuous function $u$ such that $\int _X u \, {\sf {vol}}=0$. In particular, the product $S\wedge S$ is a well-defined probability measure on $X$.

Proof of Proposition 5.4 in case (i) Let $\beta$ be a smooth form with $[\beta ]=w$. For simplicity, we denote by the same letter $P_\nu$ the operator $\int f^* ( \cdot ) \,d\nu (f)$ acting on the cohomology, on differential forms, or on currents. Write $(\alpha ^{-1}P_\nu )\beta =\beta +dd^c(h)$ for some smooth function $h$. Then,

(5.6)\begin{equation} \bigg(\frac{1}{\alpha}P_\nu\bigg)^n \beta=\beta + dd^c \bigg(\sum_{j=0}^{n-1} \frac{1}{\alpha^j}(P_\nu)^j(h)\bigg), \end{equation}

where $(P_\nu )^j(h)(x)=\int h\circ f(x) \,d\nu ^{\star j}(f)$ and $\nu ^{\star j}$ denotes the $j$th convolution power of $\nu$. Using the fact that ${\Vert (P_\nu )^j(h) \Vert }_\infty \leq {\Vert h \Vert }_\infty$ for all $j\geq 1$. We deduce that the series on the right-hand side of (5.6) converges geometrically:

(5.7)\begin{equation} \sum_{j=k}^{\ell} {\left\Vert \frac{1}{\alpha^j}(P_\nu)^j(h) \right\Vert}_\infty \leq \frac{\alpha-\alpha^{k-\ell}}{\alpha-1}\frac{{\Vert h \Vert}_\infty}{\alpha^k}\leq \frac{\alpha}{\alpha-1}\frac{{\Vert h \Vert}_\infty}{\alpha^k}. \end{equation}

Thus, if we set $h_\infty =\sum _{j\geq 0} ({1}/{\alpha ^j})(P_\nu ^*)^j(h)$ and $S=\beta + dd^c(h_\infty )$ we see that $S$ is a closed current which satisfies $P_\nu (S)=\alpha S$.

Let us show that $S$ is positive. By Lemma 5.2, there is a $P_\nu$-invariant hyperplane $W\subset H^{1,1}(X;\mathbf {R})$ such that the spectral radius of $P_{\nu \vert W}$ is $<\alpha (\nu )$. Since $w$ is nef, there is a smooth and closed form $\beta '$ such that $[\beta ']\in W$ and $\kappa :=\beta +\beta '$ is Kähler. Choose $\dim (W)$ smooth, closed $(1,1)$-forms $\gamma _i$ such that $\gamma _1=\beta '$ and the classes $[\gamma _i]$ form a basis of $W$. Then,

(5.8)\begin{equation} \frac{1}{\alpha}P_\nu \gamma_i=\sum_j Q_{i,j} \gamma_j + dd^c(u_i), \end{equation}

where $Q:=(Q_{i,j})$ is the matrix of $ ({1}/{\alpha })P_{\nu \vert W}$ in the basis $([\gamma _i])$ and the $u_i$ are smooth functions. Fix some $\eta <1$ larger than the spectral radius of $Q$. Iterating (5.8), one sees that $( ({1}/{\alpha })P_\nu )^n\gamma _i$ is the sum of a closed form bounded by $C_1\eta ^n$, plus the $dd^c$ of a function which is bounded by $C_2\sum _{j=0}^n \eta ^{n-j}\alpha ^{-j}$. Thus, for each $i$, $( ({1}/{\alpha })P)^n\gamma _i$ converges to zero in the space of currents. In particular, $( ({1}/{\alpha })P)^n\beta '$ converges to $0$, and $( ({1}/{\alpha })P)^n\kappa$ converges towards $S$, so $S$ is positive.

Let us prove that $S$ is unique. Let $T$ be a closed positive current such that $P_\nu (T)=\alpha T$ and $[T]= [S]$. Since $T-S$ is cohomologous to zero and is a difference of closed positive currents, according to [CD23c, Lemma 6.1], we can write $T-S=dd^cv$ where $v=u_1-u_2$, and each $u_i$ is an $(A\kappa _0)$-psh function ($A$ depends only of the mass of $S$ and $T$). Changing $u_i$ into $u_i-\int _Xu_i{\sf {vol}}$ we may assume that $\int _Xu_i {\sf {vol}}=0$ for $i=1,2$. From the invariance of $T-S$ under $ ({1}/{\alpha }) P_\nu$ we obtain that

(5.9)\begin{equation} \frac{1}{\alpha}P_\nu(v)=v+c \end{equation}

for some constant $c\in \mathbf {R}$; thus, $\alpha ^{-n}P_\nu ^n(v)=v+c_n$ where $c_n$ converges geometrically towards some $c_\infty \in \mathbf {R}$. From [CD23c, Lemma 6.5], there is a constant $C>1$ such that

(5.10)\begin{equation} \int_X \frac{1}{\alpha^n}\vert P_\nu^n(v)\vert {\sf{vol}}\leq \frac{C}{\alpha^n}\int_X \log(C{\Vert {\operatorname{Jac}}(f^{-1}) \Vert}_\infty)\,d\nu^{\star n}(f) \end{equation}

for all $n\geq 1$. Thanks to the moment condition (5.2) and the subadditivity property

\[ \log({\Vert {\operatorname{Jac}}((f\circ g)^{-1}) \Vert}_\infty)\leq \log({\Vert {\operatorname{Jac}}(f^{-1}) \Vert}_\infty)+ \log({\Vert {\operatorname{Jac}}(g^{-1}) \Vert}_\infty), \]

we see that

\begin{align*} \int_X \log({\Vert {\operatorname{Jac}}(f^{-1}) \Vert}_\infty)\,d\nu^{\star n}(f) &= \int_X \log({\Vert {\operatorname{Jac}}(f_n^{-1}\circ \cdots \circ f_1^{-1}) \Vert}_\infty)\,d\nu (f_1)\cdots d\nu (f_n)\\ &\leq \sum_{j=1}^n \int_X \log({\Vert {\operatorname{Jac}}(f_j^{-1} ) \Vert}_\infty) \, d\nu (f_1)\cdots d\nu (f_n) \\ &= O(n), \end{align*}

so the right-hand side of the inequality (5.10) tends to $0$ as $n$ goes to $+\infty$. Hence, $\alpha ^{-n}P_\nu ^n(v)$ converges towards $0$ in $L^1(X;{\sf {vol}})$. Since $\alpha ^{-n}P_\nu ^n(v)=v+c_n$ also converges towards $v+c_\infty$, we deduce that $v$ is a constant, namely $v=-c_\infty$, and finally $T=S$, as was to be proved.

Proof of Proposition 5.4 in case (ii) Here, we use the notation of Example 5.3. There are two closed positive currents $T^+_f$ and $T^-_f$, with continuous potentials, such that $f^*(T^\pm _f)=\lambda (f)^{\pm 1} T^\pm _f$; they are unique up to a positive scalar factor and their classes generate the isotropic lines $\mathbf {R} \theta ^\pm _f$ (see [Can14, § 5]). By convention, we choose them so that $\langle [T^+_f]\vert [T^-_f]\rangle =1$ or, equivalently, $T^+\wedge T^-$ is a probability measure; to determine them uniquely we further require $\langle [T^+_f]\vert [\kappa _0]\rangle =\langle [T^-_f]\vert [\kappa _0]\rangle$. Beware that this normalization is different from that of $\theta _f^\pm$ so a priori $[ T^\pm _f]\neq \theta _f^\pm$.

Let $w\in \mathbb {H}_X$ be of the form $w=a[T^+_f]+b[T^-_f]$, with $a$, $b>0$, and set $S=aT^+_f+bT^-_f$. Then $S$ satisfies the invariance property $ ({1}/{\alpha })P_\nu S=S$, and its uniqueness as a fixed current of $P_\nu$ in the class $w$ is obtained as in case (i).

Remark 5.5 Note that, in case (ii), the measure $S \wedge S$ is equal to $T^+_f\wedge T^-_f$ which is the measure of maximal entropy $\mu _f$ (see § 3.1 and [Can14, §§ 5.2, 8.2]).

5.2.3 Continuity properties of stationary currents

We keep the same setting as above and consider a sequence of probability measures $(\nu _n)$ with supports contained in a fixed finite set $\{ f_1, \ldots, f_m\}$:

(5.11)\begin{equation} \nu_n=\sum_i \nu_n(f_i) \delta_{f_i}, \end{equation}

with coefficients in the simplex of dimension $m-1$ determined by the constraints $\nu _n(f_i)\geq 0$ and $\sum _i \nu _n(f_i) = 1$. Assume that $(\nu _n)$ converges towards $\nu _\infty =\sum _i \nu _\infty (f_i)\delta _{f_i}$, and that each $\Gamma _{\nu _n}$ is non-elementary. For $n\in \mathbf {N}$, we denote by $w_{\nu _n}\in \mathbb {H}_X$ the eigenvector of $P_{\nu _n}$ given by Lemma 5.2, and by $S_{n}$ the current given by Proposition 5.4; we write $S_{n}=\Theta (w_{\nu _n})+dd^c u_{n}$, as in Proposition 5.4. For the measure $\nu _\infty$, we make one of the following two assumptions:

1. (a) either $\Gamma _{\nu _\infty }$ is non-elementary;

2. (b) or $\nu _\infty =\frac {1}{2} (\delta _f+\delta _{f^{-1}})$ for some loxodromic automorphism $f$, and $w_{\nu _n}$ converges to $w_{\nu _\infty }:= ({1}/{\sqrt {2}}) ([T^+_f]+[T^-_f])$, with notation as in case (ii) of Proposition 5.4.

In both cases, Proposition 5.4 provides a unique closed positive current $S_{\infty }$ such that $[S_{\infty }]=w_{\nu _\infty }$ and $P_{\nu _\infty }S_{\infty }=\alpha (\nu _\infty ) S_{\infty }$; it coincides with $ ({1}/{\sqrt 2}) (T^+_f+T^-_f)$ in case (b).

In case (a), by the uniqueness assertion of Lemma 5.2, the classes $w_{\nu _n}$ converge towards $w_{\nu _\infty }$; in case (b) this convergence holds by assumption. Note that the corresponding constants $\alpha (\nu _n)$ converge as well.

Lemma 5.6 Let $X$ be a smooth compact Kähler surface. Under the above assumptions,

1. (1) the sequence of closed positive currents $(S_{n})$ converges towards $S_{\infty }$;

2. (2) the canonical (continuous) potentials $u_{n}$ converge uniformly to that of $S_{\infty }$;

3. (3) the sequence of measures $\mu _n:=S_{n}\wedge S_{n}$ converges towards $S_{\infty }\wedge S_{\infty }$.

In case (b), $S_{\infty }\wedge S_{\infty }$ is the unique measure of maximal entropy $\mu _f$ of $f$.

Proof. The first assertion follows from the uniqueness of the current $S$ obtained in Proposition 5.4, and the compactness of the space of currents of mass $1$. The speed of convergence obtained in (5.7) shows that the sequence of potentials $u_{n}$ is equicontinuous, and by the uniqueness of the normalized potentials, it follows that $(u_{n})$ converges uniformly to $u_{\infty }$. Then the convergence of the sequence of measures $(\mu _n)$ follows from the continuity properties of wedge products of currents (see [Dem12, III.3.6]). Finally, the characterization of $S_{\infty }\wedge S_{\infty }$ in case (b) follows from Remark 5.5.

5.2.4 Singular setting

In this section, we present a variation of Proposition 5.4 in which $X$ is projective but singular; on the other hand, the class $w$ is supposed to be ample. Two main issues have to be considered when $X$ has singularities, the first is the existence of local potentials for positive closed currents, and the second is to control ${\operatorname {Jac}}(f)$. The notions we need are described in [BM14], [Dem85], and [GR65]: we present them for a (reduced and pure-dimensional) compact complex analytic surface $Y$. Let $Y^{\mathrm {reg}}$ and $Y^{\mathrm {sing}}$ denote its regular and singular parts. There is a finite cover of $Y$ by open sets $Y_\alpha \subset Y$ such that each $Y_\alpha$ is isomorphic, via an embedding $j_\alpha$, to an analytic subset of the unit ball in $\mathbf {C}^N$ (for some $N$). By definition, a $(p,q)$-form of class ${\mathcal {C}}^k$ on $Y_\alpha$ is a $(p,q)$-form on $Y_\alpha ^{\mathrm {reg}}$ which is the pull-back by $j_\alpha$ of a $(p,q)$-form of class ${\mathcal {C}}^k$ on the unit ball; a form is positive if it is induced by a positive form. By [BM14], Proposition 2.4.4, there are smooth functions $\varphi _\alpha \geq 0$ with compact support $\subset Y_\alpha$ such that $\sum _\alpha \varphi _\alpha = 1$ on $Y$. Let $\omega$ be the standard hermitian $(1,1)$-form of $\mathbf {C}^N$ and set $\kappa _\alpha := j_\alpha ^* \omega$. Then $\kappa := \sum _\alpha \varphi _\alpha \kappa _\alpha$ is a smooth positive $(1,1)$-form on $Y$. As a volume form, we shall use ${\sf {vol}} :=\kappa \wedge \kappa$. From [GR65, § 5.A, Theorems 14 and 16] and the compactness of $Y$, we get:

1. (1) the notion of $(p,q)$-form of class ${\mathcal {C}}^k$ does not depend on the local embedding $j_\alpha$;

2. (2) if $\kappa '$ is a positive hermitian form on $Y$, then $a^{-1}\kappa \leq \kappa '\leq a \kappa$ for some $a>0$;

3. (3) if $f\in \mathsf {Aut}(Y)$, the jacobian determinant ${\operatorname {Jac}}(f)$ of $f$ with respect to ${\sf {vol}}$ is a smooth, bounded function on $Y^{\mathrm {reg}}$; in particular, $\log \vert {\operatorname {Jac}}(f)\vert \in L^1(Y, {\sf {vol}})$.

A $(1,1)$-current on $Y_\alpha$ is an element of the dual of the space of smooth $(1,1)$-forms (see [Dem85]). A current $T$ on $Y_\alpha$ induces a current $(j_\alpha )_*T$ on $\mathbf {C}^N$ by the formula $\langle (j_\alpha )_* T \vert \phi \rangle := \langle T \vert (j_\alpha )^* \phi \rangle$; it is positive if $(j_\alpha )_*T$ is positive for every $\alpha$. A function $u\colon Y_\alpha \to [-\infty, +\infty [$ is psh if it is the restriction to $Y_\alpha$ of a psh function on the unit ball of $\mathbf {C}^N$ (see [FN80, Theorem 5.3.1] or [Dem85]). If, furthermore, $u$ is continuous, then $u$ is the restriction of a continuous and psh function $\tilde u$ on the unit ball (see [Ric68, Satz 2.4]). If $u$ is psh, the current $dd^c u$ is defined on $Y_\alpha$ by

(5.12)\begin{equation} \langle dd^c u, \varphi \rangle := \int_{j_\alpha(Y)} \tilde u \,dd^c \tilde \varphi \end{equation}

for every form $\varphi$ on $Y_\alpha$ induced by a $(1,1)$-test form $\tilde \varphi$ on $\mathbf {C}^N$; the integral is computed on the smooth part and is therefore equal to $\int _{Y_\alpha ^{\mathrm {reg}}} udd^c\varphi$ (see [Dem85]). A function defined on an open subset $U\subset Y$ is psh if it is psh on each $U\cap Y_\alpha$. A closed positive $(1,1)$-current $T$ on $Y$ has local (continuous) potentials if every point $x$ has a neighborhood $U$ on which $T = dd^c u$ for some (continuous) psh function on $U$; note that the existence of a local potential is a non-trivial property when $x\in Y^{\mathrm {sing}}$. If $T$ has a continuous potential $u$ in $U$, its wedge product with any closed $(1,1)$-current $S$ on $U$ is defined by

(5.13)\begin{equation} S \wedge T (\varphi) = \langle (j_{\alpha})_*S \vert \tilde u \, dd^c \tilde \varphi \rangle \end{equation}

for every smooth real-valued function $\varphi$ on $U\cap Y_\alpha$ (and any smooth extension $\tilde \varphi$ of $\varphi$ to the unit ball). This is a positive measure on $U$, see [Dem12, Chapter III.3].

Example 5.7 Let $Y$ be a (singular) complex projective surface, and $w\in {\mathrm {NS}}(Y;\mathbf {Q})$ be an ample class on $Y$. Then, there is an embedding $\iota \colon Y\to \mathbb {P}^N(\mathbf {C})$ such that the restriction of the Fubini–Study metric $\omega _{FS}$ to $\iota (Y)$ is a Kähler form representing a positive multiple of $w$. This form has smooth local potentials, because so does $\omega _{FS}$, and there is a constant $a>1$ such that $a^{-1} \kappa \leq \iota ^*\omega _{FS}\leq a \kappa$.

Proposition 5.8 Let $X$ be a (singular) complex projective surface, and let ${\sf {vol}}$ be a smooth volume form on $X$. Let $\nu$ be a probability measure on $\mathsf {Aut}(X)$ satisfying the moment condition (5.1). Assume that we are in one of the situations (i) or (ii) of Proposition 5.4, and that some real positive multiple of $w$ is an integral ample class. Then, there is a closed positive current $S$ such that:

1. (a) $P_\nu S=\alpha S$ and $[S]=w$;

2. (b) this current has continuous potentials, $S=\Theta (w)+dd^c(u)$ for a unique continuous function $u$ such that $\int _X u \, {\sf {vol}}=0$;

3. (c) if $\omega$ is a Kähler form representing the class $w$, then $( \alpha ^{-1} P_\nu )^n(\omega )$ converges towards $S$ as $n$ goes to $+\infty$.

In particular, the product $S\wedge S$ is a well-defined probability measure on $X$. Furthermore, if $T$ is another closed positive current, $P_\nu T=\alpha T$, and $T=S+dd^c(v)$ for some function $v$, then $T=S$.

The proof of properties (a), (b), and (c) is the same as that of Proposition 5.4, but here we start with $\beta =s ^{-1}\iota ^*\omega _{FS}$ instead of an arbitrary smooth form, where $\iota ^*\omega _{FS}$ is as in Example 5.7 and $s\in \mathbf {R}_+^*$ is chosen so that $sw$ belongs to ${\mathrm {NS}}(X;\mathbf {Z})$ and is very ample.

Remark 5.9 Inspecting the proof reveals that our construction coincides with Kawaguchi's construction in [Kaw06, Theorem 3.2.1]. In other words, the current $S$ coincides with the current $T$ of [Kaw06, Theorem 3.2.1], except that Kawaguchi assumed $X$ to be smooth to avoid working with Kähler forms on singular surfaces.

The only point that remains to be explained is the validity of the volume argument in the uniqueness assertion of the proposition. First, as observed above, the Jacobian of an automorphism is uniformly bounded. Second, we have to extend [CD23c, Lemma 6.5] to the singular case. The key step of this lemma is the fact that for a quasi-psh function $u$, there is a constant $c>0$ such that ${\sf {vol}} \{\vert u\vert \geq t\}\leq c\exp (-t/c)$ (see [Kis00]). To extend this result to the singular case it is enough to deal with a local psh function $u$ on a singular surface $Y_\alpha$ in the unit ball of $\mathbf {C}^N$. Consider a linear projection $\pi \colon Y_\alpha \to \mathbf {C}^2$ onto a $2$-dimensional plane which is a finite ramified cover. Then, one can define $\pi _*(u)$ outside the ramification locus $R_\pi$ of $\pi$, by $\pi _*(u)(x) = \sum _{y\in Y_\alpha, \pi (y)=x}u(y)$. This function is psh, and it is bounded, because $u$ is locally bounded; so, it extends through $R_\pi$ as a psh function. In particular, $\pi _*(u)$ satisfies ${\sf {vol}}_{\mathbf {C}^2} \{\vert \pi _*(u)\vert \geq t\}\leq c_\pi \exp (-t/c_\pi )$ for some $c_\pi >0$. Choosing finitely many such projections $\pi _j$ to ensure that $\sum _j \pi _j^*{\sf {vol}}_{\mathbf {C}^2}$ is a volume form on $Y_\alpha$, we obtain ${\sf {vol}} \{\vert u\vert \geq t\}\leq c\exp (-t/c)$ for some $c>0$, as desired.

5.3 Rational invariant classes

We now construct sequences of probability measures for which the fixed classes $w_{\nu _n}$ have good positivity and integrality properties; the last assertion makes use of the contraction $\pi _0\colon X\to X_0$ constructed in Proposition 3.9.

Proposition 5.10 Let $X$ be a smooth complex projective surface and $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(X)$ such that $\Pi _\Gamma$ is defined over $\mathbf {Q}$. Let $f$ be a loxodromic element of $\Gamma$. There is a sequence $(\nu _n)$ of probability measures on $\mathsf {Aut}(X)$ such that:

1. (1) the support $\operatorname {Supp}(\nu _n)$ is a finite subset $F$ of $\Gamma$ that does not depend on $n$ and generates a non-elementary subgroup of $\Gamma$ containing $f$;

2. (2) $\nu _n(g)$ is a positive rational number for all $g\in F$;

3. (3) the unique eigenvector $w_{\nu _n}$ of $P_{\nu _n}$ in $\mathbb {H}_X$ is an element of $\mathbf {R}_+{\mathrm {NS}}(X;\mathbf {Z})$;

4. (4) the corresponding eigenvalue $\alpha (\nu _n)$ belongs to $\mathbf {Q}_+\cap ]1,+\infty [$;

5. (5) $\nu _n$ converges to the measure $\frac {1}{2}(\delta _{f}+ \delta _{f^{-1}})$ and $w_{\nu _n}$ converges to $ (1/{\sqrt 2})({[T^+_f]+ [T^-_f]})$.

If $\Gamma$ contains a parabolic element $g$, one can furthermore assume that $g$ belongs to $F$ and that $w_{\nu _n}\in \mathbf {R}_+\pi _0^*[A_n]$ for some ample line bundle $A_n$ on $X_0$.

Proof. For the proof we use the conventions of § 3.1.2, in particular the classes $\theta _f^\pm$, which can be defined by $\theta ^\pm _f= \langle T^\pm _f\vert [\kappa _0] \rangle ^{-1} [T^\pm _f]$.

Step 1. Since the representation of $\Gamma$ on $\Pi _\Gamma$ is irreducible, it is also irreducible over $\mathbf {C}$. Indeed, if $W$ is a proper, $\Gamma$-invariant, complex subspace of $\Pi _\Gamma \otimes _\mathbf {R}\mathbf {C}$, then $W$ does not contain any non-zero real vector $u\in H^{1,1}(X;\mathbf {R})$; in particular, it does not contain any isotropic eigenvector of any loxodromic element of $\Gamma$. This implies that $W$ is contained in the orthogonal complement $(\theta _h^+)^\perp$ for all $h\in \Gamma _{\mathrm {lox}}$. But in $\Pi _\Gamma$ the intersection $\bigcap _{h\in \Gamma _{\mathrm {lox}}} (\theta _h^+)^\perp$ is defined over $\mathbf {R}$ and is $\Gamma$-invariant, so it is trivial.

Thus, according to Burnside's theorem (see [HR80]), $\Gamma$ contains a basis of the real vector space ${\sf {End}}(\Pi _\Gamma )$. More precisely, one can find a basis $(f_1^*, f_2^*, \ldots, f_N^*)$ with $N=(\dim \Pi _\Gamma )^2$ such that $f_i\in \Gamma$ for all $i$, $f_1=f$ and $f_2=f^{-1}$ (indeed, $f$ and $f^{-1}$ are linearly independent endomorphisms). In particular, the set of linear combinations $\sum _i \alpha _i f_i^*$ with $\alpha _i\geq 0$ contains a non-empty, open, and convex cone of ${\sf {End}}(\Pi _\Gamma )$.

If $\Gamma$ contains a parabolic element $g$ we can require that $g$ belongs to the basis, because $f^*$, $g^*$, and $(f^{-1})^*$ are linearly independent: indeed, $g^*$ preserves a unique isotropic line, while any linear combination of $f^*$ and $(f^{-1})^*$ preserves at least two isotropic lines.

Step 2. Set $F= \{ f_1, f_2, \ldots, f_N\}$ and $\Delta _N=\{(\nu _i)\in \mathbf {R}_+^N;\ \sum _i \nu _i=1\}$. Let $\Delta _N^\circ$ be the interior of this simplex. Points in $\Delta _N^\circ$ correspond to probability measures $\nu =\sum _i \nu _i \delta _{f_i}$ whose support is equal to $F$. When $\nu \in \Delta _N^\circ$, $\Gamma _\nu$ is non-elementary; so, by Lemma 5.2, $P_\nu$ has a unique fixed point $w_\nu$ in $\mathbb {H}_X$. As a consequence, the map $\nu \in \Delta ^\circ \mapsto w_\nu$ is continuous. If $U$ is an open subset of $\Delta ^\circ _N$, and $\nu _0$ is in $U$, then the image of $U$ by $\nu \mapsto P_\nu$ is an open subset $U'$ of the hyperplane

(5.14)\begin{equation} \bigg\{P\in {\sf{End}}(\Pi_\Gamma);\; P=\sum \alpha_i f_i,\; \sum \alpha_i=1 \bigg\}\subset {\sf{End}}(\Pi_\Gamma). \end{equation}

Now, take a vector $w'$ in $\mathbb {H}_X\cap \Pi _\Gamma$ near $w_{\nu _0}$. Since $P_{\nu _0}(\mathbb {P}(w'))$ is near $\mathbb {P}(w')$, there is a $B\in {\sf {GL}}(\Pi _\Gamma )$ close to ${\rm id}$ such that $P_{\nu _0}(\mathbb {P}(w'))=B^{-1}(\mathbb {P}(w'))$. Thus, $B\circ P_{\nu _0}$ is close to $P_{\nu _0}$ and fixes $\mathbb {P}(w')$. A positive multiple of $B\circ P_{\nu _0}$ belongs to $U'$, hence is of the form $P_{\nu '}$ for some $\nu '\in U$. Then, $w'$ is the leading eigenvector of $P_{\nu '}$ and $w'$ is in the image of $\nu \mapsto w_\nu$. This shows that $\nu \mapsto w_\nu$ contains an open set around $w_{\nu _0}$.

Step 3. Now, consider a sequence $(\nu _n)$ of elements of $\Delta _N^\circ$ converging to $a \delta _f+(1-a)\delta _{f^{-1}}$, with $0< a<1$. Normalize the fixed point $w_{\nu _n}$ by setting $\overline w_n:=\langle w_{\nu _n}\vert [\kappa _0]\rangle ^{-1} w_{\nu _n}$, so that $\langle \overline w_{n} \vert [\kappa _0]\rangle =1$ and $\overline w_n$ stays in a compact subset of $H^{1,1}(X;\mathbf {R})$. If $\overline w_{n_j}$ converges to $\overline w$ along a subsequence $(n_j)$ the limit is a nef eigenvector of the operator $af^*+(1-a)(f^{-1})^*$ associated to an eigenvalue $\geq 1$. Thus, if $a$ is small the limit must be equal to $\theta ^-_f$ and the sequence $(\overline w_n)$ converges towards this eigenvector (see Example 5.3). Conversely, if $1-a$ is small, then the limit is $\theta ^+_f$. The subset

(5.15)\begin{equation} \Delta_N^\circ(\varepsilon)=\{(\nu_i)\in \Delta_N^\circ;\ \nu_i\leq \varepsilon,\ \forall i\geq 3\} \end{equation}

is connected. Thus, the closure of its image by the continuous map $\nu \mapsto \langle w_{\nu }\vert [\kappa _0]\rangle ^{-1} w_\nu$ is a compact and connected subset of $\Pi _\Gamma$, and the intersection of these compact sets is also connected. This set is contained in the segment $[\theta _f^-, \theta _f^+]$ because it is contained in ${\overline {{\mathrm {Pos}}(X)}}$ and in the union of eigenvectors of $a f^* + (1-a)(f^{-1})^*$, for $a\in [0,1]$. Since it contains the endpoints of this segment, it actually coincides with it. From this we deduce that there exists a sequence of probability measures $\nu _n\in \Delta _N^\circ$ such that $\langle w_{\nu _n}\vert [\kappa _0]\rangle ^{-1} w_{\nu _n}$ converges to the class $\frac 12(\theta ^+_f+\theta ^-_f)$, hence:

• – $w_{\nu _n}$ converges to the class $ (1/{\sqrt 2})([T^+_f]+[T^-_f])$.

Then Example 5.3, the proof of case (ii) of Proposition 5.4, and Lemma 5.6 show that:

• – $P_{\nu _n}$ converges towards $\frac {1}{2}(f^*+(f^{-1})^*)$;

• – $\alpha (\nu _n)$ converges towards $\alpha (f)=\frac {1}{2}(\lambda (f)+1/\lambda (f))$.

Step 4. At this stage the coefficients $\nu _n(f_i)$ and the eigenvalues $\alpha (\nu _n)$ are positive real numbers. Let $U_n$ be a small open neighborhood of $\nu _n=(\nu _n(f_i))$ in $\Delta _N^\circ$. By Step 2, the image of $\nu '\in U_n\mapsto w_{\nu '}$ contains a neighborhood of $w_{\nu _n}$ in $\Pi _\Gamma \subset {\mathrm {NS}}(X;\mathbf {R})$. Thus, after a small perturbation of $\nu _n$ we may assume that $w_{\nu _n}\in \mathbf {R}_+{\mathrm {NS}}(X;\mathbf {Z})$. According to Proposition 3.9 and Remark 3.11, when $\Gamma$ contains parabolic elements, we may further choose $w_{\nu _n}$ to be proportional to the pullback $[\pi _0^*A_n]$ of an ample class.

The equation satisfied by $w_{\nu _n}$ is $\alpha (\nu _n) w_{\nu _n} = \sum _i \nu _n(f_i) f_i^*(w_{\nu _n})$. Write $w_{\nu _n}=\eta _n {\tilde {w}}_n$ for some ${\tilde {w}}_n$ in ${\mathrm {NS}}(X;\mathbf {Q})$ and $\eta _n$ in $\mathbf {R}_+$; the equation becomes

(5.16)\begin{equation} {\alpha(\nu_n)} {\tilde{w}}_n = \sum_{i=1}^N {\nu_n(f_i)}f_i^*({\tilde{w}}_n). \end{equation}

This is a linear relation of the form $\beta _0 {\tilde {w}}_n = \sum _i \beta _i f_i^*({\tilde {w}}_n)$, where ${\tilde {w}}_n$ and the $f_i^*({\tilde {w}}_n)$ belong to ${\mathrm {NS}}(X;\mathbf {Q})$ and the $\beta _i$ are positive real numbers (with $\beta _0>1$). Thus, given any $\varepsilon >0$, there is a relation of the form ${\tilde {\beta _0}}{\tilde {w}}_n = \sum _i \tilde \beta _i f_i^*({\tilde {w}}_n)$ where the coefficients $\tilde \beta _i$ are rational numbers which are $\varepsilon$-close to the original $\beta _i$. This proves that we can perturb $\nu _n$ one more time to insure that the $\nu _n(f_i)$ and $\alpha (\nu _n)$ are positive rational numbers.

5.4 Arithmetic equidistribution

Here, $X$ is a normal projective surface (possibly singular) and both $X$ and the subgroup $\Gamma$ of $\mathsf {Aut}(X)$ are defined over some number field ${\mathbf {k}}\subset {\overline {\mathbf {Q}}}$. For $y$ in $X({\overline {\mathbf {Q}}})$, let $m_y$ denote the uniform probability measure supported on the Galois orbit of $y$,

(5.17)\begin{equation} m_y=\frac{1}{\deg(y)} \sum_{y'\in \operatorname{Gal}({\overline{\mathbf{Q}}} : {\mathbf{k}})(y)}\delta_{y'}; \end{equation}

here, $\deg (y)$ is the degree of the closed point defined by $y$ or, equivalently, the cardinality of the orbit of $y$ under the action of the Galois group $\operatorname {Gal}({\overline {\mathbf {Q}}} : {\mathbf {k}})$, and the sum ranges over all points $y'$ in this orbit. A sequence $(x_j)$ of points of $X({\overline {\mathbf {Q}}})$ is generic if the only Zariski-closed subset of $X$ containing infinitely many of the $x_j$ is $X$. Equivalently, $(x_j)$ converges to the generic point of $X$ for the Zariski topology.

Theorem 5.11 Let $X$ be a normal projective surface defined over a number field ${\mathbf {k}}$. Let $\nu$ be a probability measure on $\mathsf {Aut}(X_{\mathbf {k}})$ with finite support $F$ and rational weights $\nu (f)\in \mathbf {Q}_+$, for $f$ in $F$, and such that $\Gamma _\nu$ is non-elementary. Assume that:

1. (i) the class $w_\nu$ such that $P_\nu ^*w_\nu =\alpha (\nu ) w_\nu$ is ample and contained in ${\mathrm {NS}}(X;\mathbf {Q})$;

2. (ii) $(x_j)\in X({\overline {\mathbf {Q}}})^\mathbf {N}$ is a generic sequence such that each $x_j$ is a periodic point of $\Gamma _\nu$.

Then, the sequence of probability measures $(m_{x_j})$ converges towards the measure $S_\nu \wedge S_\nu$, and this measure is $\Gamma _\nu$-invariant.

Here $w_\nu$ is given by Lemma 5.2 and $S_\nu$ is the current associated to $w_\nu$ by Proposition 5.8. It is important that $w_\nu$ be a rational class, that is $w_\nu \in {\mathrm {NS}}(X;\mathbf {Q})$ instead of just ${\mathrm {NS}}(X;\mathbf {R})$, since we rely on results of Kawaguchi, Yuan, and Zhang that require this assumption. It is also crucial that $X$ is not supposed to be smooth because this result will be applied to the model $X_0$ constructed in § 3.3.

Remark 5.12 By [Kaw08, Lee12], Theorem 5.11 also holds when $\Gamma _\nu$ is elementary (with essentially the same proof).

Example 5.13 Under the assumption of Theorem 5.11, assume furthermore that $X$ is an abelian surface. Since $\Gamma _\nu$ has a periodic point $x_1$, the stabilizer $\Gamma _{x_1}={\mathrm {Stab}}_{\Gamma _\nu }(x_1)$ has finite index in $\Gamma _\nu$; conjugating by a translation we can take $x_1$ as the neutral element for the group law of $X\simeq \mathbf {C}^2/\Lambda$. Then, the periodic points of $\Gamma _{x_1}$ (and of $\Gamma _\nu$) are exactly the torsion points of $X$ (see § 4.1). By the equidistribution theorem of Szpiro, Ullmo, and Zhang, the measures $m_{x_j}$ converge towards the Haar measure of $X$ (see [SUZ97]). In addition, $\Gamma _{x_1}$ is induced by a subgroup $\tilde \Gamma _{x_1}$ of ${\sf {GL}}_2(\mathbf {C})$ preserving the lattice $\Lambda$, and $\Gamma _\nu$ is a group of affine transformations with linear part given by $\tilde \Gamma _{x_1}$ and translation part given by the finite subset $\Gamma _\nu (0)\subset X$. Every cohomology class $u$ in $H^{1,1}(X;\mathbf {R})$ has a distinguished representative, given by the unique translation invariant $(1,1)$-form $\omega _u$ on $X$ such that $[\omega _u]=u$. Since $\Gamma _\nu$ acts by affine automorphisms, the operator $ ({1}/{\alpha })P_\nu$ preserves $\omega _{w_\nu }$, and $S_\nu =\omega _{w_\nu }$. Thus, for abelian surfaces, Theorem 5.11 corresponds to the theorem of Szpiro, Ullmo, and Zhang together with the fact that $\omega _{w_\nu }\wedge \omega _{w_\nu }$ is equal to the volume form inducing the Haar measure on $X$.

Proof of Theorem 5.11 For notational ease, set $\Gamma =\Gamma _\nu$, $w=w_\nu$, $\alpha =\alpha (\nu )$. Let $\pi \colon Y\to X$ be a minimal resolution; by [BHPV04, § III.6, Theorems (6.1) and (6.2)], it is unique up to isomorphism and $\Gamma$ lifts to a subgroup $\Gamma _Y$ of $\mathsf {Aut}(Y)$. We shall also consider $\nu$ as a measure on $\Gamma _Y$. The pull-back $\pi ^*\colon {\mathrm {Pic}}(X)\to {\mathrm {Pic}}(Y)$ is an isometric embedding for the intersection form; moreover, $\pi ^*{\mathrm {NS}}(X;\mathbf {R})$ is $\Gamma _Y$-invariant and contains classes with positive self-intersection. Thus, $\Gamma _Y$ and $\Gamma$ are both non-elementary. Moreover, $P_\nu (\pi ^*w)=\alpha \pi ^*w$ in ${\mathrm {NS}}(Y;\mathbf {R})$, so $\pi ^*w$ coincides with the unique eigenclass provided by Lemma 5.2 in ${\mathrm {NS}}(Y;\mathbf {R})$.

Case 1. Assume that ${\mathrm {Pic}}^0(X)$ is non-trivial; equivalently, ${\mathrm {Pic}}^0(Y)$ is non-trivial. Since $\Gamma _Y$ contains a loxodromic element, we deduce from [Can14, Theorem 10.1] that $Y$ is a blow-up of an abelian surface (for ${\mathrm {Pic}}^0(Y)$ is trivial when $Y$ is birationally equivalent to a rational, K3, or Enriques surfaces). But then $X$ is smooth and is a blow-up of an abelian surface. If $X$ itself is not an abelian surface, the exceptional divisor $E$ of the blow-up is $\Gamma$-invariant. From this invariance we get $\alpha \langle w\vert [E] \rangle = \langle P_\nu w \vert [E] \rangle = \langle w \vert [E] \rangle$, but since $w$ is ample and $\alpha >1$, this is a contradiction. Therefore, $X$ is abelian, and Theorem 5.11 follows from the discussion in Example 5.13.

Case 2. Assume now that ${\mathrm {Pic}}^0(X)=0$. The proof is based on standard ideas from arithmetic equidistribution theory. For the reader's convenience we provide background and details (see also [Lee12] for the applicability of arithmetic equidistribution in this context). Changing $w$ into a multiple, we assume $w\in {\mathrm {NS}}(X;\mathbf {Z})$. Multiplying the equation $\sum _f \nu (f) f^*(w)=\alpha w$ by the least common multiple $b$ of the denominators, we obtain the linear relation

(5.18)\begin{equation} \sum_{f\in F} n(f) f^*(w)=dw; \end{equation}

in which $d=b\alpha$ and the coefficients $n(f)=b\nu (f)$ are positive integers such that

(5.19)\begin{equation} \sum_{f\in F} n(f) = b < d = b \alpha \end{equation}

because $\alpha >1$. Denote by $D$ a divisor with class $w$, and by $L$ the line bundle ${\mathcal {O}}_X(D)$. Since ${\mathrm {Pic}}^0(X)$ is trivial, the Equality (5.18) implies

(5.20)\begin{equation} \bigotimes_{f\in F} (f^*L)^{\otimes n(f)} = L^{\otimes d} \end{equation}

up to an isomorphism of line bundles that we do not specify. From this identity, Kawaguchi constructs in [Kaw06, § 1] a function $\hat {h}_L\colon X({\overline {\mathbf {Q}}})\to \mathbf {R}_+$ which satisfies the relation $\sum _f n(f) {\hat {h}}_L\circ f = d{\hat {h}}_L$ and differs from the naive Weil height function associated to $L$ only by a bounded error. It will be referred to as the canonical stationary height associated to $\nu$ and $L$. This height function can be decomposed as a sum of continuous local height functions, see [Kaw06, § 4]. Arakelov theory also provides a canonical adelic metric on $(X,L)$; for each place $v$ of ${\mathbf {k}}$, there is a metric $\vert \cdot \vert _v$ on the line bundle $(X_{{\mathbf {k}}_v}, L_{{\mathbf {k}}_v})$, where ${\mathbf {k}}_v$ is an algebraic closure of the $v$-adic completion of ${\mathbf {k}}$, such that

(5.21)\begin{equation} \prod_{f\in F} \vert s(f(x)) \vert_v^{n(f)}= \vert s(x)\vert_v^d \end{equation}

for every local section $s$ of $L$ defined over ${\mathbf {k}}$. In our setting, an embedding ${\mathbf {k}}\subset \mathbf {C}$ is fixed; it corresponds to one of the places of ${\mathbf {k}}$. The adelic metric corresponding to that place gives a continuous metric on $L$. By construction, the curvature current of the metric is precisely the current $S$, here denoted by $S_\nu$, constructed in Proposition 5.8 (see Remark 5.9).

Lemma 5.14 A point $x\in X({\overline {\mathbf {Q}}})$ satisfies ${\hat {h}}_L(x)=0$ if and only if its $\Gamma _\nu$-orbit is finite.

Proof (see [Kaw06, Proposition 1.3.1.]) Let ${\mathbf {k}}'$ be any number field containing ${\mathbf {k}}$. The set $\{ x\in X({\mathbf {k}}');\ {\hat {h}}_L(x)=0\}$ is $\Gamma _\nu$-invariant and by Northcott's theorem it is finite, so every element of that set has a finite orbit. Let us prove the other implication. Iterating the relation $\sum _f n(f) {\hat {h}}_L\circ f = d{\hat {h}}_L$ and evaluating it on a periodic point $x$ yields $\alpha ^n {\hat {h}}_L(x)=\sum _{g\in \Gamma }\nu ^{\star n}(g){\hat {h}}_L(g(x))$ where $\nu ^{\star n}$ is the $n$th convolution of $\nu$. The right-hand side is bounded because ${\hat {h}}_L(g(x))$ takes only finitely many values, and on the left-hand side the term $\alpha ^n$ goes to $+\infty$; thus, ${\hat {h}}_L(x)=0$, as asserted.

Let ${\mathbf {A}}_{{\mathbf {k}}}$ denote the ring of adèles of the number field ${\mathbf {k}}$. The sections of $L$ defined over ${\mathbf {k}}$ determine a lattice $H^0(X,L)$ in $H^0(X,L)\otimes {\mathbf {A}}_{\mathbf {k}}$, and the quotient $(H^0(X,L)\otimes {\mathbf {A}}_{\mathbf {k}})/H^0(X,L)$ is therefore compact. Denote by $\overline {L}$ the line bundle $L$ endowed with its canonical adelic metric. For each place $v$, denote by $B_v\subset H^0(X,L)\otimes {\mathbf {k}}_v$ the unit ball with respect to the $v$-adic component $\vert \cdot \vert _v$ of the adelic metric of ${\overline {L}}$. Let $\lambda _L$ be a Haar measure on $H^0(X,L)\otimes {\mathbf {A}}_{\mathbf {k}}$. The quantity

(5.22)\begin{equation} \chi(X,{\overline{L}})=\log \frac{\lambda_L(\prod_{v\in M_{\mathbf{k}}} B_v)}{\lambda_L(H^0(X,L)\otimes {\mathbf{A}}_{\mathbf{k}}/H^0(X,L))} \end{equation}

does not depend on the choice of Haar measure. Taking tensor products, we get a sequence of adelic metrized line bundles $({\overline {L}}^{\otimes n})_{n\geq 1}$, and by definition the arithmetic volume of $\overline L$ is

(5.23)\begin{equation} {\widehat{{\sf{vol}}}}_\chi(X, {\overline{L}})=\limsup_{n\to +\infty} \frac{\chi(X, {\overline{L}}^{\otimes n})}{n^3/6}. \end{equation}

This is to be compared with the usual volume ${\sf {vol}}(X, L)$ of $L$, which by definition is the limsup of $ ({2}/{n^2})h^0(X,L^{\otimes n})$, as $n$ tends to $+\infty$. A fundamental inequality of Zhang asserts that if $(x_j)$ is a generic sequence in $X({\overline {\mathbf {Q}}})$,

(5.24)\begin{equation} \liminf_j \; {\hat{h}}_L(x_j)\geq \frac{{\widehat{{\sf{vol}}}}_\chi(X, {\overline{L}})}{3 {\sf{vol}}(X, L)}. \end{equation}

This follows from an adelic version of the Minkowski theorem on the existence of integer points in lattices (see, e.g., [CT09, Lemma 5.1] or [Zha95, Theorem 1.10]).

As for the usual volume, the arithmetic volume can be interpreted in terms of arithmetic intersection. Indeed, to $\overline {L}$ is associated an arithmetic degree $\widehat {\deg }(c_1(\overline {L})^3)$, and it is shown in [Zha95] that ${\widehat {{\sf {vol}}}}_\chi (X, {\overline {L}})=\widehat {\deg }(c_1(\overline {L})^3)\geq 0$ (see also [Kaw06, Theorem 2.3.1]). Thus, the existence of a generic sequence of periodic points $(x_j)$ shows that ${\widehat {{\sf {vol}}}}_\chi (X,{\overline {L}})=0$ and ${\hat {h}}_L(x_j)={\widehat {{\sf {vol}}}}_\chi (X,\overline {L})$ for all $j$.

We are now in a position to apply Yuan's equidistribution theorem (see [Yua08, BB10]): the sequence of measures $(m_{x_j})$ converges towards the probability measure $S_\nu \wedge S_\nu$ as $j$ goes to $\infty$. If $f$ is any element of $\Gamma _\nu$, the points $f(x_j)$ also form a generic sequence of $\Gamma$-periodic points. Since the actions of $\Gamma$ and $\operatorname {Gal}(\overline {\mathbf {Q}}:{\mathbf {k}})$ commute, we infer that $f_*(m_{x_j})=m_{f(x_j)}$, so taking the limit as $j\to \infty$ yields $f_*(S_\nu \wedge S_\nu )=S_\nu \wedge S_\nu$, and finally $S_\nu \wedge S_\nu$ is $\Gamma _\nu$-invariant.

5.5 Density of active saddle periodic points

Let $f$ be a loxodromic automorphism of $X$. We say that a periodic point of $f$ is active if it is contained in the support of the measure of maximal entropy $\mu _f$. From [Duj06, Can14] we know that a saddle periodic point that is not contained in any $f$-periodic curve is active (see [Can14, Theorem 8.2]).

Theorem 5.15 Let $X$ be a compact Kähler surface and let $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(X)$ that contains a parabolic automorphism. Then, given any non-empty open subset $\mathcal {V}\subset X$ (for the Euclidean topology), there exists a point $x\in \mathcal {V}$ and a loxodromic element $f\in \Gamma$ such that $x$ is an active saddle periodic point of $f$. In particular, the union of the supports of the measures $\mu _f$, for $f\in \Gamma _{\mathrm {lox}}$, is dense in $X$.

Before proceeding to the proof, let us point out the following lemma, which readily follows from Lemma 3.5, together with the fact that an irreducible curve with negative self-intersection is determined by its class in ${\mathrm {NS}}(X; \mathbf {Z})\subset {\mathrm {NS}}(X; \mathbf {R})$.

Lemma 5.16 Let $U$ and $U'$ be two disjoint open subsets of $\mathbb {P}({\mathrm {NS}}(X;\mathbf {R}))$ containing nef classes. Set

\[ A(U,U')=\{ f\in \mathsf{Aut}(X);\ f\ {\text{is loxodromic}},\ \mathbb{P}([T^+_f])\in U \ {\text{and}}\ \mathbb{P}([T^-_f])\in U'\} . \]

Then, the union of all periodic curves of all elements of $A(U,U')$ is a finite set of curves.

Proof of Theorem 5.15 Pick $g$ in $\Gamma _{\mathrm {par}}$. Since $\Gamma$ is non-elementary we can conjugate $g$ by an element of $\Gamma _{\mathrm {lox}}$ to produce a pair $g, h \in \Gamma _{\mathrm {par}}$ with distinct fixed points in $\partial \mathbb {H}_X$.

Step 1. Assume that $X$ is a blow-up of an abelian surface $A$, and pick $f$ in $\Gamma _{\mathrm {lox}}$. By Lemma 4.3, its periodic points are dense, and all of them are active because $\mu _f$ is the pull-back to $X$ of the Haar measure on $A$. Thus, any open subset of $X$ contains active saddle periodic points.

From now on, assume that $X$ is not a blow-up of an abelian surface.

Step 2. From § 3.1, $g$ preserves a unique fibration $\pi _g\colon X\to B_g$ and the automorphism induced by $g$ on $B_g$ is periodic. Replacing $g$ by some iterate, we assume that $\pi _g\circ g=\pi _g$. Let $\mathcal {U}\subset B_g$ be a small disk containing no critical value of $\pi _g$. There is a real analytic diffeomorphism $\Phi \colon \pi _g^{-1}(\mathcal {U})\to \mathcal {U}\times \mathbf {R}^2/\mathbf {Z}^2$ and a real analytic map $\varphi \colon \mathcal {U}\to \mathbf {R}^2$ such that $\pi _\mathcal {U}\circ \Phi =\pi _g$ and $g_\Phi :=\Phi \circ g \circ \Phi ^{-1}$ satisfies

(5.25)\begin{equation} g_\Phi(b,z)=(b,z+\varphi(b)) \end{equation}

for all points $(b,z)\in \mathcal {U}\times \mathbf {R}^2/\mathbf {Z}^2$. According to [Can01b, CD23b], $\varphi$ is generically of maximal rank: there is a finite set $Z\subset \mathcal {U}$ such that $(D\varphi )_b\colon T_b\mathcal {U}\to \mathbf {R}^2$ has rank $2$ for every $b\in \mathcal {U}\setminus Z$; hence, $\{b\in \mathcal {U};\ \varphi (b)\in \mathbf {Q}^2/\mathbf {Z}^2\}$ is dense in $\mathcal {U}$. If $\varphi (b)=(a_0/N,b_0/N)$ for some integers $a_0$, $b_0$, and $N$, then every point $q=(b,z)$ in the fiber is fixed by $g_\Phi ^N$ and

(5.26)\begin{equation} (Dg_\Phi^N)_x = \bigg(\begin{array}{@{}cc@{}} {\rm id}_2 & 0 \\ N(D\varphi)_b & {\rm id}_2 \end{array}\bigg). \end{equation}

Thus, in any holomorphic coordinate system $(x,y)$ in which $\pi _g$ expresses as $\pi _g(x,y)=x$, the differential of $g^N$ at the fixed point $\Phi ^{-1}(q)$ is of the form $\big (\begin{smallmatrix}1 & 0 \\ a & 1 \end{smallmatrix}\big )$ with $a\neq 0$.

Step 3. The invariant fibrations $\pi _g$ and $\pi _h$ are transversal in the complement of a proper Zariski-closed set ${\mathrm {Tang}}(\pi _g,\pi _h)$. According to Lemmas 5.16 and 3.13, we can find an integer $N>0$, and a divisor $F\subset X$ such that all elements $g^{\ell N}\circ h^{\ell N}$ with $\ell \geq 1$ are loxodromic and do not have any periodic curve outside $F$.

Step 4. Let $D$ be the union of the singular and multiple fibers of $\pi _g$ and of $\pi _h$, of ${\mathrm {Tang}}(\pi _g,\pi _h)$, and of the divisor $F$; $D$ is a divisor of $X$. Let $\mathcal {V}$ be an open subset of $X$. Then $\mathcal {V}$ contains a small ball $\mathcal {V}'$ such that:

• – $\mathcal {V}'$ does not intersect $D$;

• – $\pi _g(\mathcal {V}')$ and $\pi _h(\mathcal {V}')$ are topological disks $\mathcal {U}_g$ and $\mathcal {U}_h$ in $B_g$ and $B_h$, respectively;

• – there are local coordinates $(x,y)$ in $\mathcal {V}'$ (respectively, $x$ in $\mathcal {U}_g$ and $y$ in $\mathcal {U}_h$) such that $(\pi _{g})_{\vert \mathcal {V}'}(x,y)=x$ and $(\pi _{h})_{\vert \mathcal {V}'}(x,y)=y$.

Step 2 provides a point $(x_0,y_0)\in \mathcal {V}'$ and an integer $N>0$ such that $g^N$ fixes the fiber of $\pi _g$ through $(x_0,y_0)$ pointwise, $h^N$ fixes the fiber of $\pi _h$ through $(x_0,y_0)$ pointwise, and

(5.27)\begin{equation} (Dg^N)_{(x_0,y_0)} =\bigg(\begin{array}{@{}cc@{}} 1 & 0 \\ a & 1 \end{array}\bigg),\quad \text{and}\quad (Dh^N)_{(x_0,y_0)}=\bigg(\begin{array}{@{}cc@{}} 1 & b \\ 0 & 1 \end{array}\bigg) \end{equation}

for some non-zero complex numbers $a$ and $b$. If $\ell \in \mathbf {Z}$ is sufficiently large, $f_{\ell N}=(Dg^{\ell N})_{(x,y)}\circ (Dh^{\ell N})_{(x,y)}$ is a loxodromic automorphism, $(x_0,y_0)$ is a fixed point of $f_{\ell N}$ which is not contained in a periodic curve of $f_{\ell N}$ (because $(x_0,y_0)$ is not in $F$), which is shown to be a saddle by an explicit computation. Thus, as explained before the proof, $(x_0,y_0)$ is active, and we are done.

5.6 Measure rigidity and Kummer examples

Theorem 5.17 Let $X$ be a smooth complex projective surface and let $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$. Assume that:

1. (i) $X$ and $\Gamma$ are defined over a number field ${\mathbf {k}}\subset \overline {\mathbf {Q}}$;

2. (ii) $\Gamma$ is non-elementary and contains a parabolic automorphism.

If $\Gamma$ has a Zariski-dense set of finite orbits, then every loxodromic automorphism in $\Gamma$ is a Kummer example.

Proof. Step 1: from the Zariski-dense set of finite orbits we can extract a generic sequence of $\Gamma$-periodic points $(x_j)\in X(\overline {\mathbf {Q}})^\mathbf {N}$. Since $\Gamma$ is non-elementary, it contains a loxodromic element $f$. The isolated periodic points of $f$ are defined over ${\overline {\mathbf {Q}}}$, because $X$ and $f$ are defined over ${\overline {\mathbf {Q}}}$, and the non-isolated periodic points of $f$ form a finite number of $f$-periodic curves (see § 3.2). Thus, we can find a Zariski-dense set of $\Gamma$-periodic points $x'_i$ in $X({\overline {\mathbf {Q}}})$. If $Z\subset X$ is an irreducible curve that contains infinitely many of the $x_i'$, then $Z$ is defined over ${\overline {\mathbf {Q}}}$ too. There are only countably many curves defined over ${\overline {\mathbf {Q}}}$. Thus, by a diagonal argument, we find an infinite sequence of periodic points $x_j\in X({\overline {\mathbf {Q}}})$ such that $(x_j)$ is generic.

In what follows, $(x_j)$ denotes such a generic sequence of periodic points. Consider the contraction $\pi _0\colon X\to X_0$ of the union $D_\Gamma$ of all $\Gamma$-periodic curves (see Proposition 3.9); the group $\Gamma$ also acts on the normal projective surface $X_0$. Note that the projection $(\pi _0(x_j))\in X_0(\overline {\mathbf {Q}})^\mathbf {N}$ is also generic.

Step 2: there exists a $\Gamma$-invariant measure $\mu$ such that $\mu _f = \mu$ for all loxodromic $f$. Fix an arbitrary element $f$ in $\Gamma _{\mathrm {lox}}$. By [CD23c, Lemma 2.9], $\Pi _\Gamma$ is defined over $\mathbf {Q}$ so applying Proposition 5.10 we obtain a sequence of probability measures $(\nu _n)$. Denote by $S_{\nu _n}$ and $S_{\nu _n,0}$ the currents, on $X$ and $X_0$, respectively, given by Propositions 5.4 and 5.8; by construction $\pi _0^*S_{\nu _n,0}=S_{\nu _n}$, where the pull-back is obtained by locally pulling back the continuous potentials.

Fix an integer $n\geq 1$. Theorem 5.11 shows that the sequence of probability measures $m_{\pi _0(x_j)}$ converges towards $S_{\nu _n,0}\wedge S_{\nu _n,0}$ as $j$ goes to $+\infty$. Therefore, $S_{\nu _n,0}\wedge S_{\nu _n,0}$ coincides with the $\Gamma$-invariant probability measure $\mu _0:=\lim _{j} m_{\pi _0(x_j)}$ and does not depend on $n$. Since $S_{\nu _n, 0}$ has continuous potentials, this measure gives no mass to proper analytic subsets of $X_0$. Let $\mu$ be the probability measure which is equal to $\pi _0^*(\mu _0)$ on $X\setminus D_\Gamma$ and gives no mass to $D_\Gamma$. Since $S_{\nu _n}$ has continuous potentials, $\mu =S_{\nu _n}\wedge S_{\nu _n}$. In $X$, the sequence $(m_{x_j})$ converges to $\mu$. Indeed, if a subsequence of $(m_{x_j})$ converges towards some measure $\lambda$. Then $(\pi _0)_*\lambda =\mu _0$, and since $\mu _0$ does not charge $X_0^{\mathrm {sing}}$, we infer that $\lambda$ is equal to $\pi _0^*(\mu _0)$ on $X\setminus D_\Gamma$ and does not charge $D_\Gamma$, so $\lambda = \mu$. Thus, by compactness of the set of probability measures, $m_{x_j}$ converges towards $\mu$.

Now, we let $n\to \infty$. By Proposition 5.10(5), Proposition 5.4, and Lemma 5.6, ${S_{\nu _n}\wedge S_{\nu _n}= \mu}$ converges towards $\mu _f$ as $n$ goes to $+\infty$. Thus $\mu =\mu _f$ for all loxodromic elements $f$ in $\Gamma$. In particular, $\mu$ is $f$-ergodic, hence $\Gamma$-ergodic.

Step 3: conclusion. As already explained, $\mu$ gives no mass to proper algebraic subsets of $X$. Furthermore, Theorem 5.15 implies that the support of $\mu$ is equal to $X$. Thus, Theorem A of [CD23b] shows that $\mu$ is absolutely continuous with a smooth density. Since $\mu =\mu _f$, the Main Theorem of [CD20] implies that $(X,f)$ is a Kummer example, as was to be shown.

5.7 From Kummer examples to Kummer groups

Proposition 5.18 Let $X$ be a compact Kähler surface, and $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(X)$. Let $f\in \Gamma$ be a loxodromic element whose maximal invariant curve $D_f$ coincides with $D_\Gamma$. If $f$ is a Kummer example, then $(X, \Gamma )$ is a Kummer group.

Proof. Consider the birational morphism $\pi _0\colon X\to X_0$ contracting $D_f$ (see [Can14, § 4.1] or [CD20, Proposition 6.1]. By assumption, $f$ is a Kummer example, which entails that $X_0$ is a quotient $A/G$, with $A=\mathbf {C}^2/\Lambda$ a compact torus and $G$ a finite subgroup of $\mathsf {Aut}(A)$ generated by a diagonal map $g_0\in {\sf {GL}}_2(\mathbf {C})$ of order $2$, $3$, $4$, $5$, $6$, or $10$ (see § 4.3.2).

The group $\Gamma$ induces a group of automorphisms of $X_0$. View $X_0$ as an orbifold: its fundamental group is $\Lambda \rtimes G$ and its universal cover $\widetilde {X_0}$ is $\mathbf {C}^2$. Concretely, this means that $X_0$ is the quotient of $\mathbf {C}^2$ by the group of affine transformations with linear part in $G$ and translation part in $\Lambda$. The canonical hermitian metric on $\mathbf {C}^2$ is invariant under the affine action of $\Lambda \rtimes G$. If $\tilde {h}\colon \mathbf {C}^2\to \mathbf {C}^2$ is a lift of some $h\in \Gamma$ to $\widetilde {X_0}$,⁵ the norm of $D{\tilde {h}}_{(x,y)}$ with respect to this hermitian metric is constant along the orbits of $\Lambda \rtimes G$, hence it is bounded since the action is co-compact. This implies that the holomorphic map $(x,y)\in \mathbf {C}^2\mapsto D{\tilde {h}}_{(x,y)}$ is constant. Thus, if we denote by $\widetilde {\Gamma }$ the group of all possible lifts of all elements of $\Gamma$ to $\mathbf {C}^2=\widetilde {X_0}$, then $\widetilde {\Gamma }$ is a group of affine transformations that contains $\Lambda \rtimes G$ as a normal subgroup and satisfies $\tilde {\Gamma }/(\Lambda \rtimes G) = \Gamma$. The action by conjugation of $\tilde {\Gamma }$ on $\Lambda \rtimes G$ preserves the subgroup $\Lambda$ of translations. Therefore, $\Lambda$ is also normal in $\widetilde {\Gamma }$: this shows that $\widetilde {\Gamma }$ induces a group of automorphisms $\Gamma _A=\widetilde {\Gamma }/\Lambda$ of $A=\mathbf {C}^2/\Lambda$ that covers $X_0$, and the proof is complete.

Conclusion of the proof of Theorem B By Proposition 3.12, there exists $f\in \Gamma _{\rm lox}$ such that $D_f = D_\Gamma$. Theorem 5.17 implies that $f$ is a Kummer example, so Proposition 5.18 concludes the proof.

6. Around Theorem B: consequences and comments

6.1 Corollaries

The following corollary of Theorem B applies, for instance, to general Wehler examples defined over $\overline {\mathbf {Q}}$.

Corollary 6.1 Let $X$ be a smooth projective surface and let $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$. Assume that:

1. (i) $X$ and $\Gamma$ are defined over a number field;

2. (ii) $X$ is not an abelian surface;

3. (iii) $\Gamma$ contains a parabolic automorphism, and has no invariant curve.

Then $\Gamma$ admits only finitely many finite orbits.

Proof. Suppose $\Gamma$ has infinitely many finite orbits; since $\Gamma$ does not preserve any curve, these orbits form a Zariski dense subset. Let $g$ be a parabolic automorphism of $\Gamma$. If the fibration $\pi _g$ were $\Gamma$-invariant, then $\Gamma$ would preserve the curve $\bigcup _{y\in \Gamma (x)} \pi _g^{-1}(\pi _g(y))$ for every $\Gamma$-periodic point $x$. Thus, there is an element $h$ in $\Gamma$ that does not preserve $\pi _g$, and $h^{-1} \circ g\circ h\in \Gamma$ is a parabolic map associated to a different fibration. Hence, $\Gamma$ is non-elementary (see § 3.1.3) and Theorem B shows that $\Gamma$ is a Kummer group. But, since $X$ is not abelian, a Kummer subgroup of $\mathsf {Aut}(X)$ admits an invariant curve (see Lemma 4.7): this contradiction concludes the proof.

The next result is in the spirit of the ‘dynamical Manin–Mumford problem’.

Corollary 6.2 Let $X$ be a smooth projective surface and $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$, both defined over a number field. Suppose that $\Gamma$ is non-elementary and contains parabolic elements. Let $C\subset X$ be an irreducible curve containing infinitely many periodic points of $\Gamma$. Then:

1. (1) either $C$ is $\Gamma$-periodic and is fixed pointwise by a finite index subgroup of $\Gamma$;

2. (2) or $(X, \Gamma )$ is a Kummer group and $C$ comes from a translate of an abelian subvariety (of dimension $1$).

In both cases the genus of $C$ is $0$ or $1$. Thus, a curve of genus ${\geq }2$ contains at most finitely many periodic points of $\Gamma$.

To be specific, with the notation of § 4.3, the second assertion means the following: there is a translate $E+t$ of a $1$-dimensional abelian subvariety $E\subset A$ such that $q_X(C)=q_A(E+t)$. Moreover, if we choose the origin of $A$ at a periodic point of $\Gamma _A$, we can choose $t$ to be a torsion point of $A$. We keep this notation in the proof.

Proof. Let ${\mathrm {Per}}(C)$ be the set of periodic points of $\Gamma$ in $C$; it is Zariski dense in $C$, for $C$ is irreducible. The Zariski closure of $\Gamma ({\mathrm {Per}}(C))$ is either a $\Gamma$-invariant curve or $X$.

In the first case $C$ is contained in $D_\Gamma$, a finite index subgroup $\Gamma '\subset \Gamma$ preserves $C$, and the restriction $\Gamma ' \arrowvert _{C}$ has infinitely many periodic points in $C$. In this case $C$ has (arithmetic) genus 0 or 1 by [DJS07, Theorem 1.1]. A group of automorphisms of a curve with at least three periodic orbits is finite, because it admits a finite index subgroup fixing $3$ points; thus, a finite index subgroup of $\Gamma$ fixes $C$ pointwise.

In the second case, Theorem B shows that $(X, \Gamma )$ is a Kummer group. Since $C$ cannot be periodic, its image $q_X(C)\subset A/G$ is a non-trivial curve whose lift to $A$ contains a Zariski-dense subset of $\Gamma _A$-periodic points. Choose one of these periodic points as the origin of $A$. By Proposition 4.1 and Remark 4.2, the $\Gamma _A$-periodic points are exactly the torsion points of $A$, and conclusion (2) follows from Raynaud's theorem (formerly known as the Manin–Mumford conjecture) [Ray83].

6.2 Finitely generated groups

It turns out that $\Gamma$ is often defined over a number field when $X$ is.

Proposition 6.3 Let $X$ be a projective surface defined over a number field ${\mathbf {k}}$. Assume that $\mathsf {Aut}(X)$ contains a loxodromic element, and that $X$ is not an abelian surface. Then any finitely generated subgroup of $\mathsf {Aut}(X)$ is defined over a finite extension of ${\mathbf {k}}$.

Corollary 6.4 If $X$ is a K3 or Enriques surface defined over a number field ${\mathbf {k}}$, $\mathsf {Aut}(X)$ is finitely generated in this case (see [Ste85]) and is defined over a finite extension of ${\mathbf {k}}$.

Proof of the Proposition It is enough to show that any automorphism $f\in \mathsf {Aut}(X)$ is defined over a finite extension of ${\mathbf {k}}$. Under our assumption, $\mathsf {Aut}(X)^*\subset {\sf {GL}}(H^*(X, \mathbf {Z}))$ is infinite, $\mathsf {Aut}(X)^0$ is trivial, and the homomorphism $f\in \mathsf {Aut}(X)\mapsto f^*\in {\sf {GL}}(H^*(X, \mathbf {Z}))$ has finite kernel (see [Can14, Theorem 10.1]); more precisely, if $H$ is any ample divisor, the stabilizer of $[H]$ is a finite subgroup $\mathsf {Aut}(X;[H])$ of $\mathsf {Aut}(X)$.

Fix a finite extension ${\mathbf {k}}'$ of ${\mathbf {k}}$ and a basis of ${\mathrm {NS}}(X;\mathbf {Z})$ given by classes of divisors $D_i$ which are defined over ${\mathbf {k}}'$. Fix an ample divisor $H$ defined over ${\mathbf {k}}'$. By assumption $X$ and the $D_i$ are defined by polynomial equations over ${\mathbf {k}}'$, in some $\mathbb {P}^N$. Now, consider an automorphism $f$ of $X$, defined by polynomial formulas with coefficients in some extension $\mathbf {K}$ of ${\mathbf {k}}'$. Any field automorphism $\varphi \in \operatorname {Gal}(\mathbf {K}:{\mathbf {k}}')$ conjugates $f$ to an automorphism $f^\varphi$ of $X$: this defines a map $\varphi \in \operatorname {Gal}(\mathbf {K}:{\mathbf {k}}')\mapsto f^\varphi \in \mathsf {Aut}(X)$. On the other hand, $\langle (f^\varphi )^* [D_i]\vert [D_j]\rangle = \langle f^* [D_i]\vert [D_j]\rangle$ for any pair $(i,j)$ because the divisors $D_i$ are defined over ${\mathbf {k}}'$; thus, $(f^\varphi )^*=f^*$ on ${\mathrm {NS}}(X;\mathbf {Z})$, and $f^\varphi \circ f^{-1}$ belongs to the finite group $\mathsf {Aut}(X;[H])$, so the set $\{ f^\varphi ;\ \varphi \in \operatorname {Gal}(\mathbf {K}:{\mathbf {k}}) \}$ is finite, and we are done.

6.3 Open problems

In the case of the affine plane ${\mathbb {A}}^2$, it follows from [DF17] that any non-elementary subgroup of $\mathsf {Aut}( {\mathbb {A}}^2_{\mathbf {k}})$, for any number field ${\mathbf {k}}$, has at most finitely many finite orbits (see [DF17] for the definition of ‘non-elementary’ in this case). This motivates the following question.

Question 6.5 Is Theorem B true without assuming the existence of a parabolic element in $\Gamma$?

To understand the difficulties behind Question 6.5, let us comment on three arguments that required the hypothesis $\Gamma _{\mathrm {par}}\neq \emptyset$. First, it was used to show that $\Pi _\Gamma \subset {\mathrm {NS}}(X;\mathbf {R})$ is defined over $\mathbf {Q}$ and to construct the projective surface $X_0$ (which is then used in the construction of the canonical stationary height). The point is that, in general, the contraction of the divisor $D_\Gamma$ is a well-defined complex analytic surface, but it is not projective (see [CD20, § 11]). We expect that this issue could be circumvented by applying more advanced techniques from Arakelov geometry. Second, Theorem 5.15 also relies on the existence of parabolic elements; the point was to show that all active periodic points of all loxodromic elements of $\Gamma$ cannot be simultaneously contained in some real surface. For instance, it is unclear to us whether there can exist a real projective surface $X_\mathbf {R}$, with a non-elementary subgroup $\Gamma \subset \mathsf {Aut}(X_\mathbf {R})$, such that all periodic points of all elements $f\in \Gamma \setminus \{{\rm id}\}$ are contained in the real part $X(\mathbf {R})$ of $X$. Third, parabolic automorphisms are crucially used in the classification of $\Gamma$-invariant probability measures given in [Can01b, CD23b]. We expect that the techniques from [BH17, CD23c] will soon lead to a complete classification of $\Gamma$-invariant probability measures, for any non-elementary group $\Gamma \subset \mathsf {Aut}(X)$. Such a classification would then open the way to an extension of Theorem B to all non-elementary groups (defined over a number field).

Remark 6.6 In [Kaw13, Question 3.3], Kawaguchi formulates two interesting questions which are closely related to our main results as well as to Question 6.5.

(1) First, he asks whether two loxodromic automorphisms $f$ and $g$ of a complex projective surface $X$ with a Zariski-dense set of common periodic points automatically have the same periodic orbits. As it is formulated, the answer is no, because of Kummer groups: if we start with two loxodromic automorphisms of an abelian surface $A$ fixing the origin and generating a non-elementary subgroup, then one can blow-up the origin, and the automorphisms lift to automorphisms with the same periodic orbits (coming from torsion points of $A$), except for their fixed points on the exceptional divisors, which do differ (see Lemma 4.7, assertion (2)). Thus, his question needs to be modified by asking whether $f$ and $g$ have the same periodic points, except for finitely many of them.

(2) The second part of [Kaw13, Question 3.3] asks whether two loxodromic automorphisms of a Wehler surface having a Zariski-dense set of common periodic points automatically generate an elementary group. There are (singular) Kummer examples in the Wehler family (see [Can10, § 8.2]), and they provide counter-examples to this question. Taking these comments into consideration, Kawaguchi's second question can now be reformulated as: if two loxodromic automorphisms $f$ and $g$ of a complex projective surface $X$ have a Zariski-dense set of common periodic points, then is it true that either $f^m=g^n$ for some $m,n\geq 1$, or $f$ and $g$ generate a Kummer group? This seems harder than Question 6.5, because common periodic points do not directly provide common periodic orbits. A natural companion to the last question is: when do two loxodromic automorphisms have the same measure of maximal entropy?

One may also ask for effective bounds on the cardinality of a maximal finite $\Gamma$-invariant subset of $X(\mathbf {C})$ in terms of the data (compare [DKY22]). Proposition 2.8 says that such a bound should at least depend on the degrees of the generators of $\Gamma$.

Lastly, a natural question is whether the number field assumption in Theorem B is necessary at all: this is what the next section is about.

7. From number fields to $\mathbf {C}$

In this section we show how a specialization argument makes it possible to extend Corollary 6.1 beyond the number field case. A full generalization of Theorem B to complex coefficients would require further ideas (see § 7.4 for a short discussion). For concreteness we first treat the case of Wehler surfaces and then explain the extra ingredients required to address the general case.

7.1 Wehler surfaces

We resume the notation from § 2. The complete linear system $\vert L \vert$ parameterizing Wehler surfaces is a projective space of dimension $26$, which yields a moduli space of dimension $17$ modulo the action of $\mathsf {Aut}(\mathbb {P}^1)^3$. There is a dense, Zariski-open subset $W_0\subset \vert L \vert$ such that if $X\in W_0$, then $X$ is a smooth Wehler surface and for every $1\leq j\neq k\leq 3$, $\pi _{j,k}:X\to \mathbb {P}^1\times \mathbb {P}^1$ is a finite morphism. Let $\Gamma _X$ be the group generated by the three involutions $\sigma _i$.

Theorem 7.1 If $X$ is a smooth Wehler surface for which the projections $\pi _{j,k}\colon X\to \mathbb {P}^1\times \mathbb {P}^1$ are finite maps, then $\Gamma _X$ admits only finitely many finite orbits.

For the proof we follow the approach of [DF17, § 5 and Theorem D] closely.

Proof. Let $G = (\mathbf {Z}/2\mathbf {Z})\star (\mathbf {Z}/2\mathbf {Z})\star (\mathbf {Z}/2\mathbf {Z})$ with generators $a_1, a_2, a_3$ and let $\chi : G\to \mathsf {Aut}(X)$ be the unique homomorphism such that $\chi (a_i) = \sigma _i$. By definition, $\Gamma _X = \chi (G)$. Let $c_i$ denote the class of the curve $X\cap \{ z_i = \mathrm {C}^\mathrm {st} \}$. The subspace $\mathbf {Z} c_1\oplus \mathbf {Z} c_2 \oplus \mathbf {Z} c_3$ of ${\mathrm {NS}}(X, \mathbf {Z})$ is invariant by $\chi (G)^*\subset {\sf {GL}}({\mathrm {NS}}(X, \mathbf {Z}))$ and this representation does not depend on $X\in W_0$: the matrices of the involutions $\sigma _i^*=\chi (a_i)^*$ in the basis $(c_1,c_2,c_3)$ have constant integer coefficients (see, e.g., [CD23c, § 3]). Thus, we can define $G_{\mathrm {lox}}$ (respectively, $G_{\mathrm {par}}$) to be the set of elements $h\in G$ such that for any $X\in W_0$, $\chi (h)$ acts as a loxodromic (respectively, parabolic) map on ${\mathrm {NS}}(X, \mathbf {Z})$. Here, we implicitly use the fact that the type of $h\in \mathsf {Aut}(X)$ is the same as the type of $h^*$ in restriction to any $h^*$-invariant subspace of $H^{1,1}(X;\mathbf {R})$ on which the intersection form is not negative definite. In particular, the type of $h$ coincides with the type of $h^*$ as an isometry of ${\mathrm {Vect}}(c_1,c_2,c_3)$.

Fix a system of affine coordinates $(x,y,z)$ and write the equations of Wehler surfaces as in (2.1); this gives a system of homogeneous coordinates on $\vert L \vert$, and $\vert L \vert$ can be considered as a projective space defined over $\mathbf {Q}$. Then, endow $\vert L \vert \simeq \mathbb {P}^{26}(\mathbf {C})$ with the $\overline {\mathbf {Q}}$-Zariski topology. Fix $X\in W_0$, let $b\in \mathbb {P}^{26}$ (for ‘base point’) denote the parameter corresponding to $X$, and $S$ be the closure of $\{ b \}$ for this topology: this is a subvariety of $\mathbb {P}^{26}$ defined over $\overline {\mathbf {Q}}$ in which $b$ is, by construction, a generic point. We put $S_0=S\cap W_0$, and we restrict the universal family $\mathcal {X} \to \mathbb {P}^{26}$ of Wehler surfaces to a family $\mathcal {X}_{S_0} \to S_0$, with a fiber-preserving action of the group $G$. The fiber over $s$ is denoted by $\mathcal {X}_s$ and the natural homomorphism $G\to \mathsf {Aut}(\mathcal {X}_s)$ by $\chi _s$; thus, $X$ coincides with $\mathcal {X}_{b}$.

Lemma 7.2 For every $s\in S_0(\mathbf {C})$:

1. (1) $\mathcal {X}_s$ is a smooth $K3$ surface which does not contain any fiber of $\pi _{i,j}$, $i\neq j\in \{1,2,3\}$;

2. (2) $h\in G$ belongs to $G_{\mathrm {lox}}$ (respectively, $G_{\mathrm {par}}$) if and only if $\chi _s(h)$ is a loxodromic (respectively, parabolic) element of $\mathsf {Aut}(\mathcal {X}_s)$;

3. (3) $\chi _s(G)$ is a non-elementary subgroup of $\mathsf {Aut}(\mathcal {X}_s)$ without invariant curve.

Proof of Lemma 7.2 The first assertion follows from the results of § 2.1 and the inclusion $S_0\subset W_0$. Likewise $\chi _s(G)$ has no invariant curve by § 2.2. The second assertion follows from our preliminary remarks on the definition of $G_{\mathrm {lox}}$ and $G_{\mathrm {par}}$, and it also implies that $\chi _s(G)$ is non-elementary.

Assume now by contradiction that $\Gamma _X$ admits infinitely many finite orbits. Then the following holds.

Lemma 7.3 For every $s\in S_0(\mathbf {C})$, $\chi _s(G)$ has infinitely many finite orbits.

This lemma concludes the proof of the theorem. Indeed pick $s\in S_0(\overline {\mathbf {Q}})$. By Lemma 7.2, $\chi _s(G)$ is non-elementary, contains parabolic elements; and the Zariski closure of the set of finite orbits of $\chi _s(G)$ coincides with $\mathcal {X}_s$, as otherwise it would be an invariant curve. Then, by Theorem B, $(\mathcal {X}_s, \chi _s(G))$ must be a Kummer group. But $\mathcal {X}_s$ is a K3 surface and a Kummer group on a non-abelian surface admits an invariant curve, so that we get a contradiction with Lemma 7.2.(3).

Proof of Lemma 7.3 We first describe the set of finite $\Gamma _X$-orbits as a countable union of subvarieties by arguing as in § 2.4.1. Let $G_d$ be the intersection of the kernels of all homomorphisms from $G$ to groups of order $\leq d!$; it is a finite index subgroup of $G$. For any action of $G$, if the orbit of a point $x$ has cardinality $\leq d$, then $x$ is fixed by $G_d$. Conversely, if $x$ is fixed by $G_d$, then its $G$-orbit is finite. Define a subvariety $Z_d$ of $X$ by

(7.1)\begin{equation} Z_d = \{ x\in X;\ \forall g\in G_d,\ \chi(g )(x) = x \}. \end{equation}

Finally, put $Z = \bigcup _{d\geq 1} Z_d$. Then the $\Gamma _X$-orbit of $x\in X$ is finite if and only if $x\in Z$. We can now define a subvariety $\mathcal {Z}_d$ of $\mathcal {X}_{S_0}$ which is the fibered analogue of $Z_d$, namely

(7.2)\begin{equation} \mathcal{Z}_d = \{ (s,x);\ x\in \mathcal{X}_s, \ \forall g\in G_d, \ \chi_s(g )(x) = x \}, \end{equation}

and put $\mathcal {Z} = \bigcup \mathcal {Z}_d$. We let $\mathcal {Z}_s$ (respectively, $\mathcal {Z}_{d,s}$) be the intersection of $\mathcal {Z}$ (respectively, $\mathcal {Z}_{d}$) with $\mathcal {X}_s$.

Set $f = a_3a_2a_1 \in G$. An explicit computation shows that $f\in G_{\mathrm {lox}}$ and the eigenvalues of $\chi _s(f)^*$ on ${\mathrm {Vect}}(c_1,c_2,c_3)$ are $-1$, $\lambda (f)=9+4\sqrt {5}$, and $1/\lambda (f)$. The eigenline corresponding to $-1$ is $\mathbf {R}\cdot (c_1-3c_2+c_3)$, its orthogonal complement in ${\mathrm {Vect}}(c_1,c_2,c_3)$ is the plane $\Pi _{\chi _s(f)}$, and this plane contains the class $c_1+2c_2+c_3$. This class is ample, because it is a convex combination, with positive coefficients, of the Chern classes $c_i$ of the line bundles $\pi _i^*({\mathcal {O}}_{\mathbb {P}^1}(1))$, $i=1,2,3$. Since any invariant curve must be orthogonal to $\Pi _{\chi _s(f)}$, we deduce that $\chi _s(f)$ has no invariant curve (for all $s\in S_0$).

Now assume by contradiction that there is a parameter $t\in S_0(\mathbf {C})$ such that $\mathcal {Z}_t$ is finite. Let $P_n$ be the set of fixed points of $\chi (f^n)$, so that $P = \bigcup _n P_n$ is the set of all periodic points of $\chi (f)$; likewise, let $\mathcal {P}_n$ and $\mathcal {P}$ be their respective fibered versions. Note that $\mathcal {Z}\subset \mathcal {P}$. For fixed $n$, let $\mathcal {Y}_n$ be the (reduced) subvariety of $\mathcal {X}_{S_0}$ whose underlying set is $\mathcal {Z}\cap \mathcal {P}_n$. More precisely, the sequence of subvarieties $\mathcal {Y}_n^m:= \bigcup _{d=1}^m \mathcal {Z}_d\cap \mathcal {P}_n$ is non-decreasing with $m$, so it stabilizes, and we define $\mathcal {Y}_n =\mathcal {Y}_n^m$ for $m$ sufficiently large; its fibers will be denoted by $\mathcal {Y}_{n,s}$ ($\mathcal {Y}_{n,s}$ is the intersection of $\mathcal {Y}_n$ with $\mathcal {X}_s$, it may be non-reduced). For the generic point $b$ the cardinality of $\mathcal {Y}_{n,b}$ tends to infinity with $n$.

From this point, the argument is identical to that of Lemma 5.3 and Theorem D in [DF17].⁶ For $x\in \mathcal {Y}_{n, s}$, its multiplicity $\operatorname {mult}(x, \mathcal {Y}_{n,s})$ as a point in $\mathcal {Y}_{n, s}$ is equal to its multiplicity as a fixed point of $\chi _s(f)^n$. Nakayama's lemma implies that the function

\[ s\mapsto \sum_{x\in \mathcal{Y}_{n,s }} \operatorname{mult}(x, \mathcal{Y}_{n,s}) \]

is upper semicontinuous for the Zariski topology, hence

(7.3)\begin{equation} \sum_{x\in\mathcal{Y}_{n, t}} \operatorname{mult}(x,\mathcal{Y}_{n,t}) \geq \sum_{x\in \mathcal{Y}_{n,b }} \operatorname{mult}(x,\mathcal{Y}_{n, b }) \underset{n\to\infty}{\longrightarrow} +\infty. \end{equation}

On the other hand, $\mathcal {Z}_t$ is a finite set, so there exists $n_0$ such that for all $n\geq 1$, $\mathcal {Y}_{n, t}\subset \mathcal {P}_{n_0,t}$, and the theorem of Shub and Sullivan [SS74] asserts that for every $x\in \mathcal {P}_{n_0,t}$, the multiplicity of $x$ as a fixed point of $\chi _t(f)^n$ is bounded as $n\to \infty$. This contradicts (7.3) and concludes the proof.

7.2 Groups without invariant curve

Let us recall Theorem C.

Theorem 7.4 Let $X$ be a compact Kähler surface and let $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$. Assume that (i) $X$ is not an abelian surface, and (ii) $\Gamma$ contains a parabolic element and has no invariant curve. Then $\Gamma$ admits only finitely many finite orbits.

Proof. The idea is the same as for Theorem 7.1, however new technicalities arise. As in Corollary 6.1, $\Gamma$ is automatically non-elementary, so $X$ is projective. Arguing by contradiction, we suppose that $\Gamma$ admits infinitely many finite orbits. Applying Theorem D from § 3, we fix $f\in \Gamma _{\mathrm {lox}}$ without invariant curve. We also fix a parabolic element $g\in \Gamma$.

Step 1: geometry of $X$. Since $\Gamma$ is non-elementary, $X$ is a blow-up of an abelian surface, a K3 surface, an Enriques surface, or the projective plane (see [Can14, Theorem 10.1]). In the first three cases, there is a unique minimal model $\varphi \colon X\to \overline {X}$, and the exceptional divisor of $\varphi$ is $\mathsf {Aut}(X)$-invariant; since $\Gamma$ has no invariant curve, $X$ is already equal to its minimal model $\overline {X}$, and since $X$ is not abelian, $X$ is a K3 or an Enriques surface.

Step 2: reduction to a finitely generated subgroup. The group generated by $f$ and $g$ satisfies assumption (ii) and since it is contained in $\Gamma$ it also admits infinitely many finite orbits. From now on, we replace $\Gamma$ by $\langle f, g\rangle$ and assume $\Gamma$ to be finitely generated.

Step 3: specialization formalism. Embed $X$ into a projective space $\mathbb {P}^N_\mathbf {C}$. Fix a finite set of reduced and effective, irreducible divisors $E_j$ in $X$ whose classes form a basis of ${\mathrm {NS}}(X;\mathbf {Z})$, let $H\subset X$ be a hyperplane section, and let $\Omega$ be a non-trivial rational section of $K_X^{\otimes 2}$, where $K_X$ is the canonical bundle. If $X$ is a K3 or an Enriques surface, we assume that $\Omega$ is regular, hence does not vanish. Let $R\subset \mathbf {C}$ be the $\overline {\mathbf {Q}}$-subalgebra generated by the coefficients of a system of homogeneous equations for $X$, the $E_j$, and $H$, and by the coefficients of the formulas defining $\Omega$ and a finite symmetric set of generators of $\Gamma$. (We shall actually further enlarge $R$ in § 7.3.2.)

Let $K=\mathrm {Frac}(R)$. It is isomorphic to the function field of some (irreducible) algebraic variety $V$, defined over $\overline {\mathbf {Q}}$. There is a dense, Zariski-open subset $S$ of $V$, which may be assumed to be an affine subset, such that all elements of $R$ correspond to regular functions on $S$. Note that in what follows, by Zariski topology we mean the $\overline {\mathbf {Q}}$-Zariski topology; nevertheless, since we will use transcendental arguments, $S(\mathbf {C})$ will also be considered as a complex analytic space endowed with its Euclidean topology.

By specialization, i.e. evaluation of the elements of $R$ at $s\in S$, we can view $X\subset \mathbb {P}^N$, $\Gamma$, the $E_j$, $H$, and $\Omega$ as families over $S$; that is, there is a scheme $\mathcal {X}$ of finite type over $\overline {\mathbf {Q}}$ and a proper morphism $\pi : \mathcal {X}\to S$ endowed with a group of fiber-preserving automorphisms $\widetilde \Gamma$, together with a (complex) base point $b\in S$ so that the fiber $\mathcal {X}_b$ may be identified with $X$ and, furthermore, $\widetilde {\Gamma }_b = \Gamma$, ${\mathcal {E}}_{j,b}=E_j$, ${\mathcal {H}}_b=H$, $\widetilde \Omega _b = \Omega$, etc. The point $b\in S$ may be thought of as the generic point of $S$ (i.e. its closure for the Zariski topology is $S$) so, in particular, $b$ is a regular point of $S$ and $S$ is smooth in a complex neighborhood of $b$. If $X$ is a K3 or an Enriques surface, changing $S$ into some Zariski-dense affine open subset, we may assume that $\widetilde {\Omega }_s$ does not vanish on any $\mathcal {X}_s$.

Step 4: types of automorphisms and invariant curves.

Lemma 7.5 There is a Zariski-open subset $S_1\subset S$ such that:

1. (1) above $S_1(\mathbf {C})$, the projection $\mathcal {X}(\mathbf {C})\to S(\mathbf {C})$ is a submersion; for $s\in S_1(\mathbf {C})$, $\mathcal {X}_s$ is smooth and it is not an abelian surface;

2. (2) for $s\in S_1(\mathbf {C})$, $f_s$ is loxodromic and there exists a Euclidean neighborhood $B$ of $b$ such that for $s\in B$, $f_s$ admits no invariant curve;

3. (3) for $s\in S_1(\mathbf {C})$, $g_s$ is parabolic.

Proof of part (1) The surface $\mathcal {X}_b$ is smooth and, by construction, there is a Zariski-dense open subset $S_1$ of $S$ containing $b$ above which $\mathcal {X}\to S$ is a submersion; in particular, for $s\in S_1$, $\mathcal {X}_s$ is smooth (we will further reduce $S_1$ finitely many times in the proof, keeping the same notation). For the second conclusion, observe that $S$ is connected (for the euclidean topology), hence so is $S_1$; therefore, by Ehresmann's lemma the fibers above $S_1$ are diffeomorphic to $X$. On the other hand, a surface which is diffeomorphic to a complex torus and possesses a non-elementary group of automorphisms is automatically an abelian surface. Since $X$ is not abelian, we conclude that the same is true for any fiber $\mathcal {X}_s$, $s\in S_1$.

Proof of part (2) The loxodromic nature of $f_s$ follows from the lower semi-continuity, in Zariski topology, of the dynamical degree for birational transformations of surfaces (see [Xie15, Theorem 4.3]). Indeed, the set $\{s \in S_1; \lambda (f_s)\leq 1\}$ is Zariski closed but does not contain the generic point, so it is a proper subset, which can be removed from $S_1$.

Let us show that $f_s$ has no invariant curve for $s\in S_1$ close to $b$. Indeed, recall from Proposition 3.7 that there is a uniform bound on the degree of an invariant curve. Here we compute the degree of a curve on $\mathcal {X}_s$ (respectively, of $f_s$) with respect to the normalized ample class $\langle \mathcal {H}_s\vert \mathcal {H}_s\rangle ^{-1/2}[\mathcal {H}_s]$ induced by the hyperplane section $\mathcal {H}_s$. If $c_X$ is as in Proposition 3.7, the inequality $\frac {1}{2}[{\mathrm {Div}}(\widetilde \Omega _s)]\leq c_X \langle \mathcal {H}_s\vert \mathcal {H}_s\rangle ^{-1/2}[\mathcal {H}_s]$ is satisfied on a Zariski-open set. Then by Bishop's theorem, if $(s_i)$ is a sequence of points converging to $b$ such that $f_{s_i}$ preserves a curve $C_i$, we can extract a subsequence along which $(C_i)$ converges towards a curve $C$ in $\mathcal {X}_b$ (see [Chi89, § 16] for the relevant notions). This curve is $f_b$-invariant, which contradicts our assumption on $f$.

The proof of the third assertion of Lemma 7.5 is a little tedious and will be postponed to § 7.3.

Step 5: conclusion. We pick a point $t$ in $S_1(\overline {\mathbf {Q}})\cap B$, and argue exactly as in the case of Wehler surfaces. Indeed observe first that the assumptions of Corollary 6.1 are satisfied at the parameter $t$. Next, since all periodic points of $f_t$ of a given period are isolated, we can apply to $f_t$ the strategy of the proof of Theorem 7.1, based on Nakayama's lemma and the theorem of Shub and Sullivan; it implies that $\Gamma _t$ has infinitely many periodic orbits on $\mathcal {X}_t$, thereby reaching the desired contradiction.

7.3 Proof of Lemma 7.5(3)

By Step 1, $X$ is a K3 surface, an Enriques surface, or a blow-up of the projective plane. By semi-continuity of dynamical degrees and $\lambda (g)=1$, $g_s$ is parabolic or elliptic for every $s$ in $S_1$. Thus, we need to show that the set of parameters for which $g_s$ is elliptic is Zariski closed.

7.3.1 K3 and Enriques surfaces

Assume that $X$ is a K3 (respectively, an Enriques) surface. Above $S_1(\mathbf {C})$, every fiber $\mathcal {X}_s$ has the diffeomorphism type of $\mathcal {X}_b$, in particular it is simply connected, and $K_{\mathcal {X}_s}$ is trivial (respectively, its fundamental group is $\mathbf {Z}/2\mathbf {Z}$ and $K_{\mathcal {X}_S}^{\otimes 2}$ is trivial), so it is also a K3 (respectively, an Enriques) surface, for K3 (respectively, Enriques) are characterized by these properties (see [BHPV04, Chapter VI]). For such a surface, the group $\{h\in \mathsf {Aut}(\mathcal {X}_s);\ h^*={\rm id} {\text { on }} H^2(\mathcal {X}_s;\mathbf {Z})\}$ has at most $4$ elements (see [MN84]). The second Betti number is fixed, equal to $22$ (respectively, $10$), and if $h^*\in {\sf {GL}}(H^2(\mathcal {X}_s;\mathbf {Z}))$ has finite order, then its order divides some fixed integer $k$, because ${\sf {GL}}_{22}(\mathbf {Z})$ (respectively, ${\sf {GL}}_{10}(\mathbf {Z})$) contains a finite index, torsion free subgroup. Thus, $g_s$ is elliptic if and only if $g_s^{4k}={\rm id}$. This implies that the set of parameters $s$ for which $g_s$ is elliptic is Zariski closed and does not contain $b$, and we are done in this case.

7.3.2 Rational surfaces

Now, we assume that $X$ is rational. This case is slightly more delicate because there exists automorphisms of $\mathbb {P}^2$ of arbitrary large finite order.

Let $\pi _g\colon X\to B$ be the invariant fibration of $g$, with $B=\mathbb {P}^1$ since $X$ is rational. Replacing $g$ by some positive iterate, we assume that its action on the base $B$ is the identity. As explained in [CD12, CGL21], $\pi _g$ comes from a Halphen pencil; in particular, there is a pencil of curves in $\mathbb {P}^2$, defined by some rational function $\varphi \colon \mathbb {P}^2 --\rightarrow \mathbb {P}^1$, and a birational morphism $\eta \colon X\to \mathbb {P}^2$ that blows up the base points of this pencil (and possibly other points too), such that $\pi _g$ coincides with $\varphi \circ \eta$. The last blow-up necessary to resolve the indeterminacies of $\varphi$ provides an irreducible curve $E$ which is generically transverse to the fibration and has negative self-intersection. Let us add to our $\overline {\mathbf {Q}}$-algebra $R$ the coefficients of the formulas defining $\pi _g$, $\varphi$, $\eta$, $E$, etc. Reducing $S_1$ if necessary, we get a family of automorphisms $g_s$ preserving each fiber of a genus $1$ fibration $\pi _{g,s}\colon \mathcal {X}_s\to \mathbb {P}^1$, with an irreducible multisection $E_s$ of negative self-intersection. As for K3 and Enriques surfaces, the following lemma finishes the proof.

Lemma 7.6 There is an integer $\ell >0$ such that if $s\in S_1$ and $g_s$ is elliptic, then $g_s^\ell ={\rm id}$.

Proof. Set $m=\langle [E]\vert [F]\rangle$ where $F$ is any fiber of $\pi _g$. Above $S_1$ the surfaces $\mathcal {X}_s$ are pairwise diffeomorphic, so they have the same second Betti number and there is an integer $k>0$ such that $(h^*)^k={\rm id}$ for every elliptic automorphism of $\mathcal {X}_s$, for every $s\in S_1$. Now, if $g_s$ is elliptic, then $(g_s^k)^*[E_s]=[E_s]$ and this implies $g_s^k(E_s)=E_s$. Since $g_s$ preserves every fiber, and $E_s$ intersects every fiber in at most $m$ points, we deduce that $g_s^{k\cdot m!}$ fixes a point in each fiber. But an automorphism of a curve of genus $1$ which fixes a point has order at most $12$, so $g_s^{12k \cdot m!}={\rm id}_{\mathcal {X}_s}$, and we are done.

7.4 Discussion

It would be interesting to extend Theorem B in its general form beyond number fields, that is, without assuming that $D_\Gamma =\emptyset$. Fix $(f,g)\in \Gamma _{\mathrm {lox}}\times \Gamma _{\mathrm {par}}$, as above. The main difficulty appears in the following situation: $\Gamma$ fixes $D_\Gamma$ pointwise, and for every parameter $s\in S({\overline {\mathbf {Q}}})$, the alleged Zariski-dense set of finite orbits of $\Gamma$ specializes as a finite subset of $\mathcal {X}_s$ which intersects $(D_\Gamma )_s$. In that case, the theorem of Shub and Sullivan does not apply because it concerns isolated fixed points; so, a finer understanding of the Lefschetz fixed point formula is required. The tools introduced in [IU10] and in a chapter of Xie's thesis [Xie14] may lead to a solution of this problem.

8. Canonical vector heights

Let ${\mathbf {k}}$ be a number field and ${\overline {\mathbf {k}}}\simeq {\overline {\mathbf {Q}}}$ be an algebraic closure of ${\mathbf {k}}$. Let $X$ be a projective surface defined over ${\mathbf {k}}$ and $\Gamma$ be a subgroup of $\mathsf {Aut}(X_{\mathbf {k}})$. We consider the vector space

(8.1)\begin{equation} {\mathrm{Pic}}(X; \mathbf{R}) = {\mathrm{Pic}}(X_{\overline {\mathbf{k}}})\otimes_\mathbf{Z} \mathbf{R} \end{equation}

of $\mathbf {R}$-divisors of $X_{\overline {\mathbf {k}}}$ modulo linear equivalence; doing so, we annihilate the torsion part of ${\mathrm {Pic}}^0(X)$. Keep in mind that when $X$ is birational to an abelian variety, the vector space ${\mathrm {Pic}}^0(X; \mathbf {R}):= {\mathrm {Pic}}^0 (X )\otimes _\mathbf {Z} \mathbf {R}$ is infinite-dimensional. The Weil height machine extends to ${\mathrm {Pic}} (X; \mathbf {R})$ by $\mathbf {R}$-linearity (see [HS00, § B.3.2]). Recall from § 1.3 that a canonical vector height on $X(\overline {\mathbf {k}})$ for the group $\Gamma$ is, by definition, a function $h: {\mathrm {Pic}}(X; \mathbf {R}) \times X(\overline {\mathbf {k}}) \to \mathbf {R}_+$ such that:

1. (a) $h$ is linear with respect to the first factor $L\in {\mathrm {Pic}} (X; \mathbf {R})$;

2. (b) for every $L\in {\mathrm {Pic}} (X; \mathbf {R})$, $h(L, \cdot )$ is a Weil height associated to $L$;

3. (c) $h$ is $\Gamma$-equivariant; for every $f\in \Gamma$, $h(L, f(x)) = h(f^*L, x)$.

Note that if ${\mathrm {Pic}}(X_{\overline {{\mathbf {k}}}})$ is tensorized by $\mathbf {Q}$ instead of $\mathbf {R}$ and property (a) is stated over $\mathbf {Q}$ we get an equivalent notion. Given any $\Gamma$-invariant subspace $V\subset {\mathrm {Pic}} (X; \mathbf {R})$, one may also study the notion of restricted canonical vector height $h\colon V\times X(\overline {{\mathbf {k}}})\to \mathbf {R}$. This is most significant when $V$ contains classes with positive self-intersection, in which case it surjects onto $\Pi _\Gamma$ under the natural map $D\in {\mathrm {Pic}} (X; \mathbf {R}) \to [D]\in {\mathrm {NS}}(X; \mathbf {R})$ (see Lemma 8.3(1)). Note that we use brackets to distinguish a class in ${\mathrm {NS}}(X; \mathbf {R})$ from a class in ${\mathrm {Pic}}(X; \mathbf {R})$.

If $A_{{\mathbf {k}}}$ is an abelian variety and $\Gamma$ is a subgroup of $\mathsf {Aut}(A_{{\mathbf {k}}})$ fixing its neutral element, the Néron–Tate height on $A$ is a canonical vector height for $\Gamma$ (see [HS00, Theorem B.5.6]). The same holds if the neutral element is $\Gamma$-periodic, because in this case $\Gamma (0)$ is made of torsion points (see Remark 4.2). In this section, we describe automorphism groups of surfaces which are non-elementary, contain parabolic elements, and possess a (restricted) canonical vector height $h_{\mathrm {can}}$: Theorems E, E′, and E′′ show that $(X,\Gamma )$ is a Kummer group and $h_{\mathrm {can}}$ is derived from the Néron–Tate height.

8.1 Invariant classes and canonical vector heights

In the following lemmas, $h_{\mathrm {can}}$ is a restricted canonical vector height for $(X,\Gamma )$, defined on some $\Gamma$-invariant subspace $V_{\mathrm {can}}\subset {\mathrm {Pic}}(X;\mathbf {R})$. We say that a class $[E]$ in ${\mathrm {NS}}(X;\mathbf {R})$ is almost $\Gamma$-invariant if $f^*[E]=\pm [E]$ for all $f$ in $\Gamma$.

Lemma 8.1 Let $[E]\in {\mathrm {NS}}(X;\mathbf {R})$ be almost $\Gamma$-invariant. Let $\varphi \colon X({\overline {\mathbf {k}}})\to \mathbf {R}$ be a function. The function

\[ h_{[E],\varphi} (D,x) = h_{\mathrm{can}}(D,x)+ \langle [E] \vert D\rangle \varphi(x) \]

is a restricted canonical vector height on $V_{\mathrm {can}}\times X(\overline {{\mathbf {k}}})$ if and only if either $[E]$ is orthogonal to $V_{\mathrm {can}}$, or $\varphi \colon X({\overline {\mathbf {k}}})\to \mathbf {R}$ is bounded and satisfies $\varphi (x)[E]=\varphi (f(x))f^*[E]$ for all $f\in \Gamma$.

In this situation, we shall say that $h_{[E], \varphi }$ is derived from the height $h_{\mathrm {can}}$.

Proof. If $[E]$ is orthogonal to $V_{\mathrm {can}}$, then $h_{[E],\varphi }=h_{\mathrm {can}}$ on $V_{\mathrm {can}}\times X(\overline {{\mathbf {k}}})$ and there is nothing to prove. Otherwise, we can fix a class $D\in V_{\mathrm {can}}$ such that $\langle [E] \vert D\rangle \neq 0$. If $h_{[E],\varphi }$ is a canonical vector height, then $\varphi =\langle [E] \vert D\rangle ^{-1} (h_{[E],\varphi }-h_{\mathrm {can}})(D,\cdot )$ is bounded, because $h_{[E],\varphi }(D,\cdot )$ and $h(D,\cdot )$ are Weil heights associated to the same divisor. Furthermore, $\varphi$ satisfies $\varphi (x)[E]=\varphi (f(x))f^*[E]$ because $h_{[E],\varphi }$ and $h_{\mathrm {can}}$ are $\Gamma$-equivariant and $\langle [E]\vert f^*(D)\rangle = \langle f^*[E]\vert D\rangle$ for all $f\in \Gamma$. The reverse implication is straightforward.

Lemma 8.2 Assume that $\Gamma$ contains a loxodromic element. Let $C\subset X$ be an irreducible $\Gamma$-periodic curve. If the class of $C$ belongs to $V_{\mathrm {can}}$, or if $V_{\mathrm {can}}$ contains a $\Gamma$-periodic class $D$ such that ${\mathcal {O}}(D)_{\vert C}$ is ample, then the restriction homomorphism $\mathrm {Stab}_\Gamma (C)\ni f \mapsto f_{\vert C}$ has finite image.

Proof. If $C$ is $\Gamma$-periodic, then its self-intersection is negative, the restriction of ${\mathcal {O}}_X(-C)$ to $C$ has positive degree, and $({\mathcal {O}}_X(-C))_{\vert C}$ is therefore ample. Thus, it is enough to consider the case where $V_{\mathrm {can}}$ contains a periodic class $D$ such that ${\mathcal {O}}(D)_{\vert C}$ is ample.

After replacing $\Gamma$ by a finite index subgroup, we may assume $\Gamma (C)=C$. If $\sigma$ is an automorphism of $\mathbf {C}$ over ${\mathbf {k}}$, it maps $C$ to a $\Gamma$-invariant curve $C^\sigma$. Since $\Gamma$ contains a loxodromic element, there are only finitely many $\Gamma$-invariant irreducible curves (the components of $D_\Gamma$, see § 3.2). Thus, the orbit of $C$ under the group of automorphisms of $\mathbf {C}$ over ${\mathbf {k}}$ is finite, $C$ is defined over a number field, and $C({\overline {\mathbf {k}}})$ is dense in $C(\mathbf {C})$.

Set $\Gamma ' = \mathrm {Stab}_\Gamma (D)$, and pick $x_0\in C({\overline {\mathbf {k}}})$. Then $h_{\mathrm {can}}(D, y)= h_{\mathrm {can}}(D, x_0)$ for every $y$ in $\Gamma '(x_0)$; since $h_{\mathrm {can}}(D,\cdot )$ is a Weil height for $D$, and ${\mathcal {O}}(D)_{\vert C}$ is ample, Northcott's theorem implies that $\{ x\in C({\mathbf {k}}'); h_{\mathrm {can}}(D,x)=h_{\mathrm {can}}(D,x_0)\}$ is finite for every number field ${\mathbf {k}}'$; thus, $\Gamma '(x_0)$ is a finite set. Since $C({\overline {\mathbf {k}}})$ is infinite, we can argue as in the proof of Corollary 6.2 to deduce that $\Gamma '_{\vert C}$ is finite, as asserted.

Lemma 8.3 Assume ${\mathrm {Pic}}^0(X)=0$ and identify ${\mathrm {Pic}}(X; \mathbf {R})$ with ${\mathrm {NS}}(X; \mathbf {R})$.

1. (1) If $V_{\mathrm {can}}$ contains a class with positive self-intersection, then it contains $\Pi _\Gamma$.

2. (2) If $V_{\mathrm {can}}$ contains $\Pi _\Gamma$, and if $C$ is an irreducible rational $\Gamma$-periodic curve, then $h_{\mathrm {can}}(D,x)=0$ for every $D\in \Pi _\Gamma$ and $x\in C(\overline {{\mathbf {k}}})$.

Proof. If $V_{\mathrm {can}}$ contains a class in the positive cone it contains the limit set $\operatorname {Lim}(\Gamma )$, hence also $\Pi _\Gamma$ (see [CD23c, § 2.3]); this proves the first assertion. For the second, pick a probability measure $\nu$ on $\Gamma$ with finite support, and assume that $P_\nu ^*(D)=\alpha (\nu ) D$ for some $D$ in $\Pi _\Gamma$ and some $\alpha (\nu )>1$. Then, $\sum _f\nu (f) h_{\mathrm {can}}(D,f(x))=\alpha (\nu ) h_{\mathrm {can}}(D,x)$ by equivariance and linearity. On the other hand, ${\mathcal {O}}(D)_{\vert C}$ has degree $0$, because $\langle D\vert C\rangle =0$, and is therefore trivial because $C$ is rational. Thus, $h_{\mathrm {can}}(D,\cdot )$ is bounded on $C(\overline {{\mathbf {k}}})$. Since $\alpha (\nu )>1$, this implies that $h_{\mathrm {can}}(D, x)=0$ for every $x\in C(\overline {{\mathbf {k}}})$. To conclude, note that such eigenvectors $D$ generate $\Pi _\Gamma$ when we vary $\nu$ (see § 5.3).

8.2 From canonical vector heights to Kummer groups

Theorem 5 Let $X$ be a smooth projective surface and $\Gamma$ be a subgroup of $\mathsf {Aut}(X)$, both defined over a number field ${\mathbf {k}}$. Suppose that:

1. (i) $\Gamma$ is non-elementary and contains parabolic elements;

2. (ii) there exists a canonical vector height $h_{\mathrm {can}}$ for $(X(\overline {\mathbf {k}}), \Gamma )$ on a $\Gamma$-invariant subspace of ${\mathrm {Pic}}(X; \mathbf {R})$ which contains a divisor with positive self-intersection.

Then $(X,\Gamma )$ is a Kummer group. If, in addition, $h_{\mathrm {can}}$ is defined on ${\mathrm {Pic}} (X; \mathbf {R})\times X({\overline {{\mathbf {k}}}})$, then $X$ is an abelian surface.

The smoothness of $X$ is essential for the last conclusion to hold; for instance, if $(X_0,\Gamma )$ is a singular Kummer group with no $\Gamma$-invariant curve, we shall see that the Néron–Tate height induces a canonical vector height on ${\mathrm {Pic}} (X_0; \mathbf {R})\times X_0({\overline {{\mathbf {k}}}})$.

The remainder of this subsection is devoted to the proof of Theorem E. Let us already observe that once $(X,\Gamma )$ is known to be a Kummer group, the last conclusion follows from Lemmas 4.7 and 8.2. Thus, all we have to show is that $(X,\Gamma )$ is a Kummer group.

8.2.1 Reduction to ${\mathrm {Pic}}^0(X)=0$

Suppose ${\mathrm {Pic}}^0(X)\neq \{ 0 \}$. Then, $\Gamma$ being non-elementary, [Can14, Theorem 10.1] shows that $X$ is either an abelian surface or a blow-up of such a surface along a finite orbit of $\Gamma$, and by definition $(X, \Gamma )$ is a Kummer group.

Thus, from now on, we assume ${\mathrm {Pic}}^0(X)=\{ 0 \}$ and identify ${\mathrm {Pic}} (X; \mathbf {R})$ with ${\mathrm {NS}}(X; \mathbf {R})$.

8.2.2 A key lemma

Assumption (ii) provides a canonical vector height $h_{\mathrm {can}}$ for $(X, \Gamma )$ defined on $\Pi _\Gamma$ (see Lemma 8.3). Recall from [Sil91, Kaw08] that for every $f\in \Gamma _{\mathrm {lox}}$ there exist canonical heights $h_f^\pm$, respectively associated to the classes $\theta _f^\pm$, such that $h_f^+(f(x)) = \lambda (f) h_f^+(x)$ and $h_f^-(f^{-1}(x)) = \lambda (f) h_f^-(x)$. They satisfy:

• – $h_f^\pm \geq 0$ on $X(\overline {\mathbf {k}})$;

• – if $D_f$ denotes the maximal invariant curve of $f$, then, for $x\in X(\overline {\mathbf {k}})$, $h_f^+(x)+ h_f^-(x) = 0$ if and only if $x$ is a periodic point or $x\in D_f$ (see [Kaw08, § 5]).

Furthermore, any Weil height $h$ associated to $\theta _f^+$ such that $h (f(x)) = \lambda (f) h (x)$ coincides with $h_f^+$: indeed $k := h - h_f^+$ is bounded because $h$ and $h_f^+$ are Weil heights associated to the same class, so the relation $k (f(x)) = \lambda (f) k (x)$ forces it to be identically zero. Thus, the next lemma follows immediately from the defining properties (a), (b), and (c) (see [Kaw13, Proposition 3.4] or [Bar04, § 1]).

Lemma 8.4 If ${\mathrm {Pic}}^0(X)=\{0\}$ and if $h_{can}$ is a canonical vector height for $(X, \Gamma )$ defined on $\Pi _\Gamma$, then $h_{\mathrm {can}}(\theta _f^\pm, \cdot ) = h_f^\pm (\cdot )$ for every loxodromic $f\in \Gamma$.

Remark 8.5 If $x$ belongs to the maximal invariant curve $D_\Gamma$ and $c$ belongs to $\Pi _\Gamma$ then ${h_{\mathrm {can}}(c,x) = 0}$. Indeed for every $f\in \Gamma _{\mathrm {lox}}$, $D_\Gamma \subset D_f$ so $h_{\mathrm {can}}(\theta _f^\pm, x)=h^+_f(x)=0$, and since the classes $(\theta _f^\pm )_{f \in \Gamma _{\mathrm {lox}}}$ span $\Pi _\Gamma$, the result follows by linearity. This extends the second assertion of Lemma 8.3 to invariant curves which are not rational.

Now, recall that the classes $\theta _f^\pm$ are normalized by $\langle \theta _f^\pm \vert [\kappa _0]\rangle = 1$. Let us view $\mathbb {H}_X$ and $\mathbb {P}(\mathbb {H}_X)$ as subsets of $\{ u\in H^{1,1}(X;\mathbf {R});\ \langle u \vert u \rangle >0, \langle u \vert [\kappa _0]\rangle = 1 \}$. Setting

(8.2)\begin{equation} \widetilde \Pi_\Gamma = \Pi_\Gamma\cap \{ \langle \cdot \vert [\kappa_0]\rangle = 1 \}, \end{equation}

$\operatorname {Lim}(\Gamma )$ can now be viewed as a subset of $\widetilde \Pi _\Gamma$ which generates $\Pi _\Gamma$ as a vector space. The starting point of the proof of Theorem E is the following key lemma, inspired by the approach of Kawaguchi in [Kaw13].

Lemma 8.6 In addition to the assumptions of Theorem E, suppose that:

1. (iii) there exists $f\in \Gamma _{\mathrm {lox}}$ such that $[\theta _f^+, \theta _f^-]\cap \mathrm {Int}(\mathrm {Conv}(\operatorname {Lim}(\Gamma )))\neq \emptyset$, where $\mathrm {Conv}(\cdot )$ is the convex hull and $\mathrm {Int}(\cdot )$ stands for the interior relative to $\widetilde \Pi _\Gamma$.

Then $(X, \Gamma )$ is a Kummer group.

Proof. Set $d=\dim \widetilde \Pi _\Gamma$. Replacing ${\mathbf {k}}$ by a finite extension, we may assume that the birational morphism $\pi _0\colon X\to X_0$ constructed in Proposition 3.9 is defined over ${\mathbf {k}}$; this morphism contracts the maximal $\Gamma$-invariant curve $D_\Gamma$.

Let $\nu$ be a probability measure on $\Gamma$, whose support is finite and contains $f$ as well as elements of $\Gamma _{\mathrm {par}}$. Let $w_\nu$ be the eigenvector of the operator $P_\nu$ for the eigenvalue $\alpha (\nu )$ given by Lemma 5.2. As in Proposition 5.10, we may assume that $w_\nu$ is a rational class and is the pull-back of an ample class $[A_0]$ on $X_0$; by multiplying $w_\nu$ by a positive integer, we also assume that $w_\nu$ is an integral class.

Let $L$ be the line bundle given by the class $w_\nu$, and $\hat {h}_L$ be the associated canonical stationary height, as in the proof of Theorem 5.11. This is the unique Weil height such that $\sum _h\nu (h) \hat {h}_L\circ h = \alpha (\nu ) \hat {h}_L$. By the linearity of the canonical vector height and the uniqueness of $\hat {h}_L$, we get $\hat {h}_{L}(\cdot )=h_{\mathrm {can}}(w_\nu,\cdot )$.

Pick $w = a\theta _f^++b\theta _f^-$ in the interior of $\mathrm {Conv}(\operatorname {Lim}(\Gamma ))$, with $a$, $b$ in $\mathbf {R}_+$ and $a+b=1$. Then by linearity and Lemma 8.4, $h_{\mathrm {can}}(w, \cdot ) = ah_f^++bh_f^-$. Caratheodory's theorem provides a subset $\Lambda$ of $\operatorname {Lim}(\Gamma )$ such that $\vert \Lambda \vert = d+1$ and $w$ belongs to the interior of the simplex $\mathrm {Conv}(\Lambda )$. By the density of fixed points of loxodromic elements in $\operatorname {Lim}(\Gamma )$, we may assume that $\Lambda$ is made of classes $\theta ^+_{g}$ for $g$ in a finite subset $\Lambda _\Gamma$ of $\Gamma _{\mathrm {lox}}$. If $\varepsilon >0$ is small enough, $w-\varepsilon w_\nu$ stays in $\operatorname {Int}(\mathrm {Conv}(\Lambda ))$; so, there are positive coefficients $\beta _g$, for $g\in \Lambda _\Gamma$, such that $w-\varepsilon w_\nu = \sum _{g\in \Lambda _\Gamma } {\beta _g}\theta ^+_g$. By the linearity of $h_{\mathrm {can}}$, we infer that

(8.3)\begin{equation} a h_f^+(\cdot) + bh_f^- (\cdot) = \sum_{g\in \Lambda_\Gamma} {\beta_g} h_g^+(\cdot) +\varepsilon \hat{h}_{L}(\cdot). \end{equation}

Now, if $x\in X(\overline {\mathbf {k}})$ is $f$-periodic, then $h_f^+(x)=h_f^-(x)=0$, and since $\hat {h}_{L}$ and the $h_g^+(x)$ are non-negative, we deduce that $\hat {h}_L(x)=0$. The line bundle $L$ is the pull-back of an ample line bundle $A_0$ on $X_0$; thus, by Lemma 5.14, the $\Gamma _\nu$-orbit of $\pi _0(x)$ in $X_0$ is a finite set. Since $f$ has a Zariski-dense set of periodic points, Theorem B implies that $(X,\Gamma _\nu )$ is a Kummer group.

Since we can further choose $\Gamma _\nu$ to contain any a priori given finite subset of $\Gamma$, Propositions 3.12 and 5.18 show that $(X,\Gamma )$ is a Kummer group.

From this point, the proof of Theorem E is completed in two steps. We first deal with the case $\dim \Pi _\Gamma \leq 4$ by directly checking assumption (iii) of Lemma 8.6. This covers general Wehler surfaces (which is the setting of [Kaw13]) since $\dim \Pi _\Gamma =3$ in this case. The general case is treated in a second stage by a dimension reduction argument.

8.2.3 Conclusion when $\dim \Pi _\Gamma \leq 4$

Since $\Gamma$ is non-elementary, $\dim \Pi _\Gamma \geq 3$, so we need to consider the cases $\dim \Pi _\Gamma =3$ and $\dim \Pi _\Gamma =4$.

For $\dim \Pi _\Gamma =3$, i.e. $d=\dim (\widetilde {\Pi }_\Gamma )=2$, the intersection of $\widetilde {\Pi }_\Gamma$ with the positive cone is the Klein model of the hyperbolic disk $\mathbb {H}^2$. If assumption (iii) is not satisfied, then for every $f\in \Gamma _{\mathrm {lox}}$, $\operatorname {Lim}(\Gamma )$ is entirely contained on one side of the geodesic $[\theta _f^+, \theta _f^-]$. Fix $4$ points in $\operatorname {Lim}(\Gamma )\subset \partial \mathbb {H}^2\simeq {\mathbb {S}}^1$, labelled in circular order $(p_1, p_2, p_3, p_4)$. Lemma 3.3 provides elements $f$ and $g$ in $\Gamma _{\mathrm {lox}}$ such that $(\theta _f^+, \theta _g^+, \theta _f^-, \theta _g^-)$ is arbitrary close to $(p_1, p_2, p_3, p_4)$. Then $[\theta _f^+, \theta _f^-]$ intersects $[\theta _g^+, \theta _g^-]$ transversally in the disk $\mathbb {H}^2$, so $\operatorname {Lim}(\Gamma )$ intersects both sides of $[\theta _f^+, \theta _f^-]$, a contradiction.

Now assume $\dim \Pi _\Gamma =4$, i.e. $d=3$. Then $\mathrm {Conv}({\operatorname {Lim}(\Gamma )})$ is a convex body in dimension $3$. The conclusion relies on the following lemma (see below for a proof).

Lemma 8.7 Let $p_1, \ldots, p_5$ be five points in general position in $\mathbf {R}^3$. Then, there is a pair of indices $i\neq j$ such that the line segment between $p_i$ and $p_j$ intersects the interior of the convex hull of $p_1$, $\ldots$, $p_5$.

Indeed, fix such a $5$-tuple of points in $\operatorname {Lim}(\Gamma )$ and approximate the given pair $(p_i,p_j)$ by $(\theta ^+_f,\theta ^-_f)$, for some $f\in \Gamma _{\mathrm {lox}}$. Then, $[\theta _f^+, \theta _f^-]$ intersects the interior of $\mathrm {Conv}({\operatorname {Lim}(\Gamma )})$, and Lemma 8.6 finishes the proof of Theorem E (when $\dim (\Pi _\Gamma )\leq 4$).

Proof of Lemma 8.7 The general position assumption implies that there exists $\beta _i\neq 0$ such that $\sum _i\beta _ip_i=0$ and $\sum _i\beta _i=0$. After a permutation of the $p_i$ and possibly replacing the $\beta _i$ by their opposite, we may assume that

(8.4)\begin{equation} \beta_1 < 0 < \beta_2\leq \beta_3 \leq \beta_4 \leq \beta_5 \quad \text{or}\quad \beta_1 \leq \beta_2 < 0 < \beta_3 \leq \beta_4 \leq \beta_5. \end{equation}

In the first case, $p_1$ lies in the interior of the simplex spanned by $p_2, \ldots, p_5$. In the second case, the point

(8.5)\begin{equation} \frac{-\beta_1p_1-\beta_2p_2}{-\beta_1-\beta_2}= \frac{\beta_3p_3+\beta_4p_4+\beta_5p_5}{\beta_3+\beta_4+\beta_5} \end{equation}

lies in the interior of the convex hull of $p_1, \ldots, p_5$ and in the interior of the line segment between $p_1$ and $p_2$.

Remark 8.8 The theorem of Steinitz (see [Gru03, § 13.1]) is a far-reaching generalization of Lemma 8.7. There is no analogue of this lemma in higher dimension (see [Gru03, § 4.7]), hence the need for a different argument when $\dim \Pi _\Gamma \geq 5$.

8.2.4 Conclusion of the proof of Theorem E

Recall from Lemma 3.1 that $g^*$ is virtually unipotent for every $g\in \Gamma _{\mathrm {par}}$. Thus, if we pick a pair of parabolic elements $g_1$, $g_2$ in $\Gamma$ with distinct invariant fibrations, some positive iterates $g_1^N$ and $g_2^N$ satisfy the assumption of the following lemma.

Lemma 8.9 Let $g_1$ and $g_2$ be parabolic elements in $\mathsf {Aut}(X)$, with distinct invariant fibrations and such that $g_1^*$ and $g_2^*$ are unipotent. Then, $\Gamma _0 := \langle g_1, g_2\rangle$ is non-elementary and $\dim (\Pi _{\Gamma _0})\leq 4$.

Proof. Since $\pi _{g_1}\neq \pi _{g_2}$, $\Gamma _0$ is non-elementary (see § 3.1.3). The subspace $W:=\mathrm {Fix}(g_1^*)\cap \mathrm {Fix}(g_2^*)$ of ${\mathrm {NS}}(X;\mathbf {R})$ is fixed pointwise by $\Gamma _0$. Thus, $W^\perp$ is $\Gamma _0$-invariant, it contains $\Pi _{\Gamma _0}$ (see [CD23c, Proposition 2.8]), and all we need to show is that $\dim (W^\perp )\leq 4$. To see this, note that a unipotent Euclidean isometry is the identity, thus if $g\in {\sf {O}}^+(1,d)$ is parabolic and unipotent, the structure of parabolic isometries of $\mathbb {H}_d$ (see [FL12, § I.5]) implies that $\mathrm {Fix}(g^*)\subset \mathbf {R}^{d+1}$ is a subspace of codimension $2$, and we are done.

Lemma 8.9 and § 8.2.3 imply that $(X, \langle g_1, g_2\rangle )$ is a Kummer group for every pair of unipotent elements $g_1, g_2\in \Gamma _{\mathrm {par}}$ generating a non-elementary subgroup. By Proposition 3.12 we can choose $f\in \langle g_1, g_2 \rangle$ such that $D_f = D_\Gamma$, hence from Proposition 5.18 we conclude that $(X, \Gamma )$ is a Kummer group, and Theorem E is established.

8.3 Canonical vector heights on abelian surfaces

In this section, $A$ is an abelian surface, defined over some number field ${\mathbf {k}}$ and $\Gamma \subset \mathsf {Aut}(A_{\mathbf {k}})$ is non-elementary. Denote by $h_{\mathrm {NT}}\colon {\mathrm {Pic}}(A)\times A(\overline {{\mathbf {k}}})\to \mathbf {R}$ the Néron–Tate height on $A$; it vanishes identically on the torsion part of ${\mathrm {Pic}}(A)$, so we may also consider it as a function on ${\mathrm {Pic}}(A;\mathbf {R})\times A(\overline {{\mathbf {k}}})$. When $0\in A$ has a finite $\Gamma$-orbit, $h_{\mathrm {NT}}$ is a canonical vector height (see [HS00, Theorem B.5.6]).

Let $h_{\mathrm {can}}$ be a restricted canonical vector height for $(A_{\mathbf {k}},\Gamma )$, defined on some $\Gamma$-invariant subspace $V_{\mathrm {can}}$ of ${\mathrm {Pic}}(A;\mathbf {R})$. Our goal is to compare it with $h_{\mathrm {NT}}$.

By definition, a divisor $D$ on $A$ is symmetric if $[-1]^*D$ is linearly equivalent to $D$, where $[m]$ denotes multiplication by $m$; likewise it is antisymmetric if $[-1]^*D\simeq -D$ or equivalently if $D\in {\mathrm {Pic}}^0(A)$ (see [HS00, Proposition A.7.3.2]). If $f\in \mathsf {Aut}(A)$ fixes the origin, it commutes to $[-1]$, so that $f^*$ preserves symmetry and antisymmetry.

Remark 8.10 Any class $[D]\in {\mathrm {NS}}(A)$ can be lifted to a symmetric divisor class $D\in {\mathrm {Pic}}(A)$, which is unique up to a 2-torsion element in ${\mathrm {Pic}}^0(A)$. Thus, $D$ admits a unique symmetric lift in ${\mathrm {Pic}}(A;\mathbf {R})$. By using such a lift it makes sense to consider also $h_{\mathrm {NT}}(\cdot, \cdot )$ (respectively, $h_{\mathrm {can}}(\cdot, \cdot )$) as a function on ${\mathrm {NS}}(A;\mathbf {R})\times A(\overline {{\mathbf {k}}})$ (respectively, on the projection of $V_{\mathrm {can}}$ in ${\mathrm {NS}}(A;\mathbf {R})$). This observation will be used repeatedly in the following.

Remark 8.11 The Picard number of any complex abelian surface satisfies $\rho (A)\in \{ 1, 2, 3, 4 \}$. When $\mathsf {Aut}(A)$ contains a non-elementary group $\Gamma$, we obtain $3 \leq \dim \Pi _\Gamma \leq \rho (A) \leq 4$. Moreover, $\rho (A)=4$ if and only if $A$ is isogenous to $B\times B$, for some elliptic curve $B$ with complex multiplication (see [BL04, Ex. 10 p. 142]).

Proposition 8.12 If $V_{\mathrm {can}}$ contains ${\mathrm {Pic}}^0(A)\otimes _\mathbf {Z}\mathbf {R}$, then $\Gamma$ has a finite orbit in $A(\overline {{\mathbf {k}}})$.

Proof. In this proof it is enough to consider $h_{\mathrm {can}}$ as a function on ${\mathrm {Pic}}^0(A)\times X(\overline {{\mathbf {k}}})$, by composing with the natural homomorphism ${\mathrm {Pic}}^0(A)\to {\mathrm {Pic}}^0(A;\mathbf {R})$.

Step 1: if $D$ is an element of ${\mathrm {Pic}}^0 (A)$, then for every $f\in \Gamma _{\mathrm {lox}}$, every periodic point $x$ of $f$ satisfies $h_{\mathrm {can}}(D,x)=0$. Assume $f^q(x)=x$ for some $q\geq 1$. The endomorphism $f^q-{\rm id}$ is an isogeny of $A$ because $f$ is loxodromic (see § 4.2). Thus, its dual $(f^q)^*-{{\rm id}}$ is an isogeny of ${\mathrm {Pic}}^0(A)$ and we can find $E\in {\mathrm {Pic}}^0(A)$ such that $(f^q)^*E- E=D$. By equivariance $h_{\mathrm {can}}((f^q)^*E,x)=h_{\mathrm {can}}(E,x)$, and then by linearity $h_{\mathrm {can}}(D,x)=0$.

Step 2: let ${\mathbf {k}}'$ be a finite extension of ${\mathbf {k}}$ and let $P$ be a subset of $A({\mathbf {k}}')$. If, for every $D\in {\mathrm {Pic}}^0(A)$, the set $\{ h_{\mathrm {NT}}(D,x);\ x\in P \}\subset \mathbf {R}$ is bounded, then $P$ is finite. To see this, consider the abelian group $A({\mathbf {k}}')$; by the Mordell–Weil theorem, its rank is finite, so modulo torsion it is isomorphic to $\mathbf {Z}^r$ for some $r\geq 0$. Set $W_{{\mathbf {k}}'}=A({\mathbf {k}}')\otimes _\mathbf {Z}\mathbf {R}$, a real vector space of dimension $r$. Let $H$ be an ample symmetric divisor on $A_{\overline {{\mathbf {k}}}}$, then $h_{\mathrm {NT}}(H,\cdot )$ determines a positive-definite quadratic form on $V$; let $\langle \cdot \vert \cdot \rangle _H$ be the bilinear pairing associated to $h_{\mathrm {NT}}(H, \cdot )$. If $s$ is an element of $A(\overline {{\mathbf {k}}})$, and $t_s\in \mathsf {Aut}(A_{\overline {{\mathbf {k}}}})$ is the translation by $s$, then $D_s:=H-t_s^*H$ is an element of ${\mathrm {Pic}}^0(A)$ and $h_{\mathrm {NT}}(D_s, \cdot )$ induces an affine linear form $A({\mathbf {k}}')\to \mathbf {R}$; namely, $h_{\mathrm {NT}}(D_s, \cdot )=-2\langle s \vert \cdot \rangle _H$. Since $\langle \cdot \vert \cdot \rangle _H$ is positive definite on $W_{{\mathbf {k}}'}$ (see [HS00, Proposition B.5.3]), one can find $r$ elements $s_i\in A({\mathbf {k}}')$ such that the linear forms $\ell _i:=\langle s_i \vert \cdot \rangle _H$ constitute a basis of the dual of $W_{{\mathbf {k}}'}$. Our assumption says that each $\ell _i(P)$ is a relatively compact subset of $\mathbf {R}$; this implies that $P$ is contained in a compact, hence finite, subset of the lattice $A({\mathbf {k}}')\subset V$.

Step 3: $\Gamma$ has a finite orbit. Let $f$ be a loxodromic element of $\Gamma$, and $x$ be a fixed point of $f$. Its $\Gamma$-orbit is made of fixed points of conjugates of $f$. Note that $\Gamma (x)$ is contained in $A({\mathbf {k}}')$ for some finite extension of ${\mathbf {k}}$. By the first step, $h_{\mathrm {can}}$ vanishes on ${\mathrm {Pic}}^0(A)\times \Gamma (x)$. Since $h_{\mathrm {can}}$ and $h_{\mathrm {NT}}$ are Weil heights, $\vert h_{\mathrm {can}}(D,\cdot ) -h_{\mathrm {NT}}(D, \cdot ) \vert \leq B(D)$ for each divisor class $D\in {\mathrm {Pic}}^0(A)$, where $B(D)\geq 0$ depends on $D$. Thus, $\vert h_{\mathrm {NT}}(D, \Gamma ( x)) \vert \leq B(D)$ for every $D\in {\mathrm {Pic}}^0(A)$, and the second step implies that $\Gamma (x)$ is finite.

Proposition 8.13 Assume that the neutral element has a finite $\Gamma$-orbit. Then $h_{\mathrm {can}}$ coincides with the Néron–Tate height on:

• – the set of symmetric divisors whose numerical class belongs to $\Pi _\Gamma$;

• – the set of antisymmetric divisors;

whenever one of these sets is contained in $V_{\mathrm {can}}$.

In the following proofs, we denote by $\Pi _\Gamma ^{\mathrm {s}}$ the subspace ${\mathrm {Pic}}(A;\mathbf {R})$ made of symmetric elements $E\in {\mathrm {Pic}}(A;\mathbf {R})$ such that $[E]\in \Pi _\Gamma$.

Proof. Let $\Gamma _0\leq \Gamma$ be the finite index subgroup fixing the origin. Let us show that $h_{\mathrm {can}} = h_{\mathrm {NT}}$ on $\Pi _\Gamma ^{\mathrm {s}}\times A(\overline {{\mathbf {k}}})$. For this, we use Remark 8.10, identify $\Pi _\Gamma ^{\mathrm {s}}$ with $\Pi _\Gamma$, and consider $h_{\mathrm {can}}$ and $h_{\mathrm {NT}}$ as functions on $\Pi _\Gamma \times A(\overline {{\mathbf {k}}})$. Now, if $f\in \Gamma _{0,{\mathrm {lox}}}$, we get $h_{\mathrm {NT}}(\theta ^+_f,\cdot )=h_{\mathrm {can}}(\theta ^+_f,\cdot )$ because the difference is bounded on $A(\overline {{\mathbf {k}}})$, and is multiplied by $\lambda (f)>1$ under the action of $f$ (as in Lemma 8.4). Since the classes $\theta ^+_f$, for $f\in \Gamma _{\mathrm {lox}}$, generate $\Pi _\Gamma$, our claim is established.

Let us now deal with antisymmetric divisors. Identifying ${\mathrm {Pic}}^0(A_{\overline {\mathbf {k}}})$ with the dual abelian variety $A^\vee _{\overline {\mathbf {k}}}$ of $A$, we have to show that $h_{\mathrm {can}}$ coincides with $h_{\mathrm {NT}}$ on $A^\vee ({\mathbf {k}}')$ for every finite extension ${\mathbf {k}}'$ of ${\mathbf {k}}$. By the Mordell–Weil theorem $A^\vee ({\mathbf {k}}')$ is a finitely generated abelian group so

(8.6)\begin{equation} W^\vee_{{\mathbf{k}}'}:=A^\vee({\mathbf{k}}')\otimes_\mathbf{Z}\mathbf{R} \end{equation}

is a real vector space of dimension $r$, for some $r<+\infty$. Consider the function $\Phi :(D, x) \mapsto h_{\mathrm {can}}(D,x)-h_{\mathrm {NT}}(D,x)$. When $D$ is fixed, $\Phi (D, \cdot )$ is bounded: $\vert \Phi (D, x) \vert \leq B(D)$ for all $x\in A(\overline {\mathbf {k}})$. On the other hand, when $x$ is fixed, $\Phi _x(D) := \Phi (D, x)$ defines a linear form $\Phi _x\colon W^\vee _{{\mathbf {k}}'}\to \mathbf {R}$. Applying the previous boundedness property to $f(x)$, for $f$ ranging in $\Gamma _0$, and using the equivariance $\Phi (D, f(x)) = \Phi (f^*D, x)$ we obtain that for every $x\in A(\overline {\mathbf {k}})$, $\Phi _x$ is bounded on every $\Gamma _0^*$-orbit $\Gamma _0^*(D)\subset W^\vee _{{\mathbf {k}}'}$.

We claim that this forces $\Phi _x$ to vanish, which is the desired result. For this we analyze the dual action of $\Gamma _0$. Let $f$ be a loxodromic element of $\Gamma _0$, and $f^\vee _{{{\mathbf {k}}'}}$ be the induced linear map on $W^\vee _{{\mathbf {k}}'}=A^\vee ({\mathbf {k}}')\otimes _\mathbf {Z}\mathbf {R}$. Let $L_f$ be the linear lift of $f$ to $\mathbf {C}^2$, as in §§ 4.1 and 4.2.

Lemma 8.14 The endomorphism $f^\vee _{{{\mathbf {k}}'}}$ is semi-simple and its complex eigenvalues are complex conjugate to those of $L_f$; none of them has modulus $1$.

Let us take this for granted and conclude the proof. Since $f^\vee _{{{\mathbf {k}}'}}$ is semi-simple, $W^\vee _{{\mathbf {k}}'}$ is a direct sum of $f^\vee _{{{\mathbf {k}}'}}$-invariant irreducible factors $\bigoplus W^\vee _i$, each of dimension $1$ or $2$. For each $W^\vee _i$, denote by $\lambda _i$ the corresponding eigenvalue of $f^\vee _{{{\mathbf {k}}'}}$, and pick some $D_i\in W^\vee _i\setminus \{0\}$. If $W^\vee _i$ is a line, then $\lambda _i\in \mathbf {R}^*$ and $\vert \lambda _i \vert \neq 1$. Since $\Phi _x$ is bounded on $\{ (f^\vee _{{{\mathbf {k}}'}})^n(D_i);\ n\in \mathbf {Z} \}$, the line $W^\vee _i$ is contained in $\ker \Phi _x$. If $W^\vee _i$ is a plane, then $f^\vee _{{{\mathbf {k}}'}} \arrowvert _{W^\vee _i}$ is a similitude with $\vert \lambda _i \vert \neq 1$ and ${\mathrm {Arg}}(\lambda _i)\neq 0\mod (2\pi \mathbf {Z})$. If $\Phi _{x} \arrowvert _{W^\vee _i}\neq 0$, $\{ \vert \Phi _x \vert \leq B(D_i) \}\cap W^\vee _i$ is a strip, which furthermore contains the orbit $\{ (f^\vee _{{{\mathbf {k}}'}})^n(D_i), n\in \mathbf {Z} \}$. This is not compatible with the properties of $\lambda _i$, and this contradiction shows that $W^\vee _i \subset \ker \Phi _x$, so finally $\Phi _x = 0$, as claimed.

Proof of Lemma 8.14 The complex torus underlying $A^\vee _\mathbf {C}$ is isomorphic to a quotient of the space of $\mathbf {C}$-antilinear forms on $\mathbf {C}^2$. Thus, if $f\in \mathsf {Aut}(A)$ is induced by a linear map $L_f\in {\sf {GL}}_2(\mathbf {C})$, the automorphism of $A^\vee$ determined by $f^*$ is induced by the conjugate transpose $\overline L_f^t$ (see [BL04, § 2.4]). When $f$ is loxodromic, the eigenvalues of $L_f$ satisfy $\vert \alpha \vert <1<\vert \beta \vert$; we deduce that the automorphism of $\mathsf {Aut}(A^\vee _\mathbf {C})$ determined by $f^*$ is also loxodromic, with eigenvalues $\overline {\alpha }$ and $\overline {\beta }$, and the minimal polynomial of $\overline L_f^t$ is $(X-\overline {\alpha })(X-\overline {\beta })$. Let $P$ be the minimal, real, unitary polynomial such that $(X-\overline {\alpha })(X-\overline {\beta })$ divides $P$ (by construction $\deg (P)\in \{ 2, 3,4 \}$ and $P$ has no repeated factors). Since $P( \overline L_f^t) = 0$, we infer that $P(f^\vee _{{\mathbf {k}}'}) =0$ and the result follows.

Proposition 8.15 Let $A_{\mathbf {k}}$ be an abelian surface defined over a number field ${\mathbf {k}}$. Let $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(A_{\mathbf {k}})$, for which the neutral element $0\in A({\mathbf {k}})$ is periodic. Then one of the following situation occurs:

1. (1) ${\mathrm {NS}}(A, \mathbf {R}) = \Pi _\Gamma$ and the Néron–Tate height is the unique canonical vector height on ${\mathrm {Pic}}(A;\mathbf {R})$;

2. (2) ${\mathrm {NS}}(A, \mathbf {R}) = \Pi _\Gamma \overset {\perp }\oplus \mathbf {R} [E]$ for some $[E]\in {\mathrm {NS}}(A;\mathbf {R})\setminus \{0\}$, and the canonical vector heights on ${\mathrm {Pic}}(A;\mathbf {R})$ are exactly the functions of the form $h_{\mathrm {can}} (D, x) = h_{\mathrm {NT}} (D, x) + \langle [E] \vert D\rangle \varphi (x)$, where $\varphi \colon A({\overline {\mathbf {k}}})\to \mathbf {R}$ is any bounded function such that $\varphi (f(x)) f^*[E]=\varphi (x)[E]$ for all $f$ in $\Gamma$.

Proof. When ${\mathrm {NS}}(A, \mathbf {R}) = \Pi _\Gamma$, Proposition 8.13 and the decomposition of any divisor class as a sum $D=D^{\mathrm {s}}+D^{\mathrm {a}}$ with $D^{\mathrm {s}}$ symmetric and $D^{\mathrm {a}}$ antisymmetric imply that $h_{\mathrm {can}}=h_{\mathrm {NT}}$. Thus, by Remark 8.11 we may assume that $\rho (A)=4$ and $\dim (\Pi _\Gamma )=3$. Pick $[E]\in \Pi _\Gamma ^\perp \setminus \{ 0\}$. The line $\mathbf {R}[E]$ is $\Gamma$-invariant, and the intersection form is negative on $\mathbf {R}[E]$; as a consequence, there is a homomorphism $\alpha _{[E]}\colon \Gamma \to \{+1, -1\}$ such that $f^*[E]=\alpha (f)[E]$ for all $f\in \Gamma$. Then for fixed $x$,

(8.7)\begin{equation} \Delta_x(D)=h_{\mathrm{can}}(D,x)-h_{\mathrm{NT}}(D,x), \end{equation}

defines a linear form on ${\mathrm {Pic}}(A;\mathbf {R})$, which by Proposition 8.13 vanishes identically on $\Pi _\Gamma ^{\mathrm {s}}$. Thus, $\Delta (D,x)=\langle [E]\vert D\rangle \varphi (x)$ for some real valued function $\varphi$, and the conclusion follows from Lemma 8.1.

8.4 Synthesis

8.4.1 Canonical vector heights

Putting together Theorem E and Proposition 8.15 gives the following.

Theorem 6 Let $X$ be a smooth projective surface, defined over a number field ${\mathbf {k}}$. Let $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(X_{\mathbf {k}})$ that contains parabolic elements. Let $h_{\mathrm {can}}$ be a canonical vector height on ${\mathrm {Pic}}(X;\mathbf {R}) \times X({\overline {{\mathbf {k}}}})$ for the group $\Gamma$. Then, $X$ is an abelian surface and $h_{\mathrm {can}}$ is derived from a translate of the Néron–Tate height by a periodic point $y$ of $\Gamma$:

\[ h_{\mathrm{can}}(D,x)=h_{\mathrm{NT}}(D,x+y)+\langle [E]\vert D\rangle \, \varphi(x) \]

for some almost-invariant class $[E]\in {\mathrm {NS}}(X;\mathbf {R})$ and some bounded function $\varphi \colon X(\overline {{\mathbf {k}}})\to \mathbf {R}$ such that $\varphi (f(x)) f^*[E]=\varphi (x)[E]$ for $f\in \Gamma$.

Note that $h_{\mathrm {can}}$ is just a translate of $h_{\mathrm {NT}}$ when $E$ is numerically trivial.

8.4.2 Restricted canonical vector heights

Let us add the assumption

(8.8)\begin{equation} {\mathrm{Pic}}^0(X)=0, \end{equation}

to the hypotheses of Theorem E. Our goal is to describe all possibilities for $(V_{\mathrm {can}}, h_{\mathrm {can}})$.

Since ${\mathrm {Pic}}^0(X)=0$, $X$ is not a blow-up of an abelian surface and Theorem E implies that $(X,\Gamma )$ is a Kummer group of type (2), (3), (4), or (5) in the nomenclature of § 4.3.2. We make use of the notation of §§ 4.3.1 and 4.3.2. The origin $0\in A$ is a fixed point of the cyclic group $G$, and the orbit $\Gamma _A(0)$ is finite. Since $G$ is generated by a finite-order homothety $(x,y)\mapsto (\alpha x, \alpha y)$ on $A$, $G$ acts trivially on ${\mathrm {NS}}(A;\mathbf {R})$ and on symmetric divisors. Thus, ${\mathrm {NS}}(A/G;\mathbf {R})$ can be identified to ${\mathrm {NS}}(A;\mathbf {R})$ and to the subspace of ${\mathrm {Pic}}(A;\mathbf {R})$ generated by symmetric divisors; let

(8.9)\begin{equation} \iota\colon {\mathrm{NS}}(A;\mathbf{R}) \to {\mathrm{NS}}(X;\mathbf{R}) \end{equation}

denote the corresponding embedding, given by $\iota =q_X^*(q_A)_*$. On the space of symmetric divisors, the Néron–Tate height is $G$-invariant and $\Gamma$-equivariant, so it induces a canonical vector height $h_{\mathrm {NT}}^{A/G}(\cdot, \cdot )$ on $A/G$ for ${\overline {\Gamma }}_A$. Then, it induces a restricted canonical vector height on $\iota ({\mathrm {NS}}(A;\mathbf {R}))\times X(\overline {{\mathbf {k}}})$, namely

(8.10)\begin{equation} h_{\mathrm{NT}}^X: (D,x)\longmapsto h_{\mathrm{NT}}^{A/G} ((q_X)_*D, q_X(x)). \end{equation}

In what follows, we denote by $E_i$ the disjoint irreducible rational curves contracted by $q_X$ (see Lemma 4.7); their classes generate $\iota ({\mathrm {NS}}(A;\mathbf {R}))^\perp \subset {\mathrm {NS}}(X;\mathbf {R})$. The height $h_{\mathrm {NT}}^X$ vanishes on $\bigcup _i E_i(\overline {{\mathbf {k}}})$, because the $E_i$ are mapped to torsion points of $A$.

Lemma 8.16 We have $\Pi _\Gamma =\iota (\Pi _{\Gamma _A})\subset V_{\mathrm {can}} \subset \iota ({\mathrm {NS}}(A;\mathbf {R}))$.

Proof. The first equality comes from the equivariance of $q_X$ and $q_A$. The first inclusion follows from Lemma 8.3 and the assumption (ii) of Theorem E. It remains to prove the last inclusion. If $V_{\mathrm {can}}$ is not contained in $q_X^*({\mathrm {NS}}(A/G;\mathbf {R}))$, there is an index $i$, and a class $D$ in $\Pi _\Gamma ^\perp \cap V_{\mathrm {can}}$ such that $\langle D\vert E_i\rangle > 0$, i.e. $\mathcal {O}(D) \arrowvert _{E_i}$ is ample. The action of $\Gamma$ on $\Pi _\Gamma ^\perp$ factorizes through a finite group (see [CD23c, Lemma 2.9]), so $D$ is $\Gamma$-periodic and by Lemma 8.2, $\Gamma \arrowvert _{E_i}$ is finite; this contradicts Lemma 4.7, and the conclusion follows.

Let $D$ be an element of $\Pi _\Gamma$. By Lemma 8.3, $h_{\mathrm {can}}(D,x)=0$ for all $x\in \bigcup _i E_i(\overline {{\mathbf {k}}})$. Thus, $(D,x)\mapsto h_{\mathrm {can}}(\iota (D), q_X^{-1}(q_A(x)))$ is a well-defined restricted canonical vector height on $\Pi _{\Gamma _A}\times A(\overline {{\mathbf {k}}})$ (see Remark 8.10), which gives height $0$ to the fixed points of elements of $G\setminus \{{\rm id}\}$. By Proposition 8.13, this height coincides with the Néron–Tate height on $\Pi _{\Gamma _A}\times A(\overline {{\mathbf {k}}})$.

This yields a complete description of $h_{\mathrm {can}}$ when $V_{\mathrm {can}}=\Pi _\Gamma$.

By Lemma 8.16 and Remark 8.11, the remaining possibility is that $\dim (V_{\mathrm {can}})=4$ and $\dim (\Pi _\Gamma )=3$. Choose an almost $\Gamma _A$-invariant class $[E]$ in ${\mathrm {NS}}(A;\mathbf {R})$, as in Proposition 8.15, and a divisor $F$ in $X$ such that $[F]=\iota ([E])$. Each element $D\in V_{\mathrm {can}}$ decomposes as a sum

(8.11)\begin{equation} D= D' + \frac{\langle [F] \vert D\rangle}{\langle [F] \vert [F]\rangle} [F] \end{equation}

with $D'$ in $\Pi _\Gamma$. Then, for $x$ in $\bigcup _i E_i(\overline {\mathbf {k}})$, we get

(8.12)\begin{equation} h_{\mathrm{can}}(D,x)=\frac{\langle [F] \vert D\rangle}{\langle [F] \vert [F]\rangle} h_{\mathrm{can}}([F],x). \end{equation}

Define a function by setting $\psi (x)=\langle [F] \vert [F]\rangle ^{-1}h_{\mathrm {can}}([F],x)$ on $\bigcup _i E_i(\overline {{\mathbf {k}}})$ and $\psi (x) = 0$ otherwise. It satisfies the equivariance $\psi (f(x))f^*[F]=\psi (x)[F]$ because $h_{\mathrm {can}}$ is equivariant and $[F]$ is almost invariant, and it is bounded because ${\mathcal {O}}(F)_{\vert E_i}$ is trivial for each $E_i$. Now, if we set

(8.13)\begin{equation} h_{\mathrm{can}}'(D,x)=h_{\mathrm{can}}(D,x)- \langle [F] \vert D\rangle \,\psi(x) \end{equation}

we get a new restricted canonical vector height on $V_{\mathrm {can}}\times X(\overline {{\mathbf {k}}})$ that vanishes on $\bigcup _i E_i(\overline {{\mathbf {k}}})$. This height comes from a canonical vector height on $A/G$, and since as seen before ${\mathrm {NS}}(A/G; \mathbf {R})$ can be identified to ${\mathrm {NS}}(A; \mathbf {R})$, it yields a canonical vector height for $(A,\Gamma _A)$ restricted to the space of symmetric divisors. The second assertion of Proposition 8.15 entails that this last height is derived from the Néron–Tate height for some function $\varphi$; since $\Gamma _A$ contains $G$, and $G$ fixes $[E]$, $\varphi$ is $G$-invariant. Coming back to $X$, we get that $h_{\mathrm {can}}$ is derived from the Néron–Tate height too. In formulas,

(8.14)\begin{equation} h_{\mathrm{can}}(D,x)=h_{\mathrm{NT}}^X(D,x)+ \langle [F] \vert D\rangle \, \Phi(x), \end{equation}

where $\Phi \colon X({\overline {{\mathbf {k}}}})\to \mathbf {R}$ is a bounded function which satisfies $\Phi (f(x))f^*[F]=\Phi (x)[F]$ for $f\in \Gamma$. This function is equal to $\psi$ on $\bigcup _i E_i(\overline {{\mathbf {k}}})$ and to $\varphi \circ q_X$ on its complement.

To conclude, using the above notation, let us summarize these results in a (somewhat imprecise) statement.

Theorem 7 Let $X$ be a smooth projective surface, defined over a number field ${\mathbf {k}}$, and such that ${\mathrm {Pic}}^0(X_{\overline {{\mathbf {k}}}})=0$. Let $\Gamma$ be a non-elementary subgroup of $\mathsf {Aut}(X_{\mathbf {k}})$ containing parabolic elements. Let $h_{\mathrm {can}}$ be a restricted canonical vector height on $V_{\mathrm {can}} \times X({\overline {{\mathbf {k}}}})$ for the group $\Gamma$, where $V_{\mathrm {can}}\subset {\mathrm {Pic}} (X; \mathbf {R})$ is $\Gamma$-invariant and contains classes with positive self-intersection. Then $(X,\Gamma )$ is a Kummer group associated to an abelian surface $A$, $V_{\mathrm {can}}$ is contained in $\iota ({\mathrm {NS}}(A; \mathbf {R}))$ and:

• – either $V_{\mathrm {can}} = \Pi _\Gamma$ and $h_{\mathrm {can}}$ coincides with the Néron–Tate height $h_{\mathrm {NT}}^X$;

• – or $\Pi _\Gamma$ is a codimension-1 subspace of $V_{\mathrm {can}}$ and $h_{\mathrm {can}}$ is derived from $h_{\mathrm {NT}}^X$.