Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T19:40:55.808Z Has data issue: false hasContentIssue false
  • English
  • Français

A Feynman integral via higher normal functions

Part of: Surfaces and higher-dimensional varieties Families, fibrations Quantum field theory; related classical field theories $K$-theory in number theory

Published online by Cambridge University Press:  06 August 2015

Spencer Bloch ,
Matt Kerr  and
Pierre Vanhove
Spencer Bloch
Affiliation:
5765 S. Blackstone Ave., Chicago, IL 60637, USA email [email protected]
Matt Kerr
Affiliation:
Department of Mathematics, Campus Box 1146, Washington University in St. Louis, St. Louis, MO 63130, USA email [email protected]
Pierre Vanhove
Affiliation:
Institut des Hautes Études Scientifiques, Le Bois-Marie, 35 route de ChartresF-91440 Bures-sur-Yvette, France Institut de physique théorique, Université Paris Saclay, CEA, CNRS, F-91191 Gif-sur-Yvette, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the Feynman integral for the three-banana graph defined as the scalar two-point self-energy at three-loop order. The Feynman integral is evaluated for all identical internal masses in two space-time dimensions. Two calculations are given for the Feynman integral: one based on an interpretation of the integral as an inhomogeneous solution of a classical Picard–Fuchs differential equation, and the other using arithmetic algebraic geometry, motivic cohomology, and Eisenstein series. 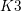Both methods use the rather special fact that the Feynman integral is a family of regulator periods associated to a family of $K3$ surfaces. We show that the integral is given by a sum of elliptic trilogarithms evaluated at sixth roots of unity. This elliptic trilogarithm value is related to the regulator of a class in the motivic cohomology of the 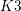$K3$ family. We prove a conjecture by David Broadhurst which states that at a special kinematical point the Feynman integral is given by a critical value of the Hasse–Weil 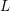$L$-function of the 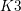$K3$ surface. This result is shown to be a particular case of Deligne’s conjectures relating values of 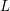$L$-functions inside the critical strip to periods.

Keywords

Feynman graphvariation of mixed Hodge structuresmotiveselliptic trilogarithmEisenstein serieshigher normal function

MSC classification

Primary: 81T18: Feynman diagrams
Secondary: 19F27: Étale cohomology, higher regulators, zeta and $L$-functions 14J28: $K3$ surfaces and Enriques surfaces 14D07: Variation of Hodge structures
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 12 , December 2015 , pp. 2329 - 2375
Copyright
© The Authors 2015 

References

Adams, L., Bogner, C. and Weinzierl, S., The two-loop sunrise graph with arbitrary masses, J. Math. Phys. 54 (2013), 052303.CrossRefGoogle Scholar
Adams, L., Bogner, C. and Weinzierl, S., The two-loop sunrise graph in two space-time dimensions with arbitrary masses in terms of elliptic dilogarithms, J. Math. Phys. 55 (2014), 102301.CrossRefGoogle Scholar
Bailey, D. H., Borwein, J. M., Broadhurst, D. and Glasser, M. L., Elliptic integral evaluations of Bessel moments, J. Phys. A 41 (2008), 205203.CrossRefGoogle Scholar
Batyrev, V., Variations of the mixed Hodge structure of affine hypersurfaces in algebraic tori, Duke Math. J. 69 (1993), 349–409.CrossRefGoogle Scholar
Batyrev, V., Dual polyhedra and mirror symmetry for Calabi–Yau hypersurfaces in toric varieties, J. Algebraic Geom. 3 (1994), 493–535.Google Scholar
Beilinson, A., Higher regulators of modular curves, in Applications of algebraic K-theory to algebraic geometry and number theory (Boulder, CO, 1983), Contemporary Mathematics, vol. 55 (American Mathematical Society, Providence, RI, 1986), 1–34.Google Scholar
Beilinson, A. and Levin, A., The elliptic polylogarithm, in Motives, Proceedings of Symposia in Applied Mathematics, vol. 55, eds Jannsen, U., Kleiman, S. and Serre, J.-P. (American Mathematical Society, Providence, RI, 1994), 123–190; Part 2.CrossRefGoogle Scholar
Bern, Z., Dixon, L. J. and Kosower, D. A., Progress in one loop QCD Computations, Annu. Rev. Nucl. Part. Sci. 46 (1996), 109–148.CrossRefGoogle Scholar
Bertin, M.-J., Mahler’s measure and L-series of K3 hypersurfaces, in Mirror symmetry V, AMS/IP Studies in Advanced Mathematics, vol. 38, eds Lewis, J., Yau, S.-T. and Yui, N. (2006), 3–18.Google Scholar
Blasius, D., On the critical values of Hecke L-series, Ann. of Math. (2) 124 (1986), 23–63.CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and the Beilinson conjectures, Contemp. Math. 58 (1986), 65–79.Google Scholar
Bloch, S., The moving lemma for higher Chow groups, J. Algebraic Geom. 3 (1993), 537–568.Google Scholar
Bloch, S., Esnault, H. and Kreimer, D., On motives associated to graph polynomials, Comm. Math. Phys. 267 (2006), 181–225.CrossRefGoogle Scholar
Bloch, S. and Vanhove, P., The elliptic dilogarithm for the sunset graph, J. Number Theory 148 (2015), 328–364.CrossRefGoogle Scholar
Borwein, J. M. and Salvy, B., A proof of a recursion for Bessel moments, Exp. Math. 17 (2008), 223–230.CrossRefGoogle Scholar
Britto, R., Loop amplitudes in gauge theories: modern analytic approaches, J. Phys. A 44 (2011), 454006.CrossRefGoogle Scholar
Broadhurst, D., Schwinger’s banana numbers and $L$-series, letter (2011).Google Scholar
Broadhurst, D., Multiple zeta values and modular forms in quantum field theory, in Computer algebra in quantum field theory eds Schneider, C. and Blümlein, J. (Springer, Wien, 2013), 33–72.CrossRefGoogle Scholar
Caron-Huot, S. and Henn, J. M., Iterative structure of finite loop integrals, J. High Energy Phys. 1406 (2014), 114–157.CrossRefGoogle Scholar
Deligne, P., Théorie de Hodge II, Publ. Math. Inst. Hautes Études Sci. 40 (1971), 5–57.CrossRefGoogle Scholar
Deligne, P., Valeurs de Fonctions L et Périodes d’Intégrales, Proc. Sympos. Pure Math. 33 (1979), 313–346; Part 2.CrossRefGoogle Scholar
Deninger, C. and Scholl, A., The Beilinson conjectures, in L-functions and arithmetic (Durham, 1989), London Mathematical Society Lecture Note Series, vol. 153 (Cambridge University Press, Cambridge, 1991), 173–209.CrossRefGoogle Scholar
Dolgachev, I., Mirror symmetry for lattice polarized K3 surfaces, J. Math. Sci. 81 (1996), 2599–2630.CrossRefGoogle Scholar
Doran, C. and Kerr, M., Algebraic K-theory of toric hypersurfaces, Commun. Number Theory Phys. 5 (2011), 397–600.CrossRefGoogle Scholar
Ellis, R. K., Kunszt, Z., Melnikov, K. and Zanderighi, G., One-loop calculations in quantum field theory: from Feynman diagrams to unitarity cuts, Phys. Rep. 518 (2012), 141–250.CrossRefGoogle Scholar
Elvang, H. and Huang, Y.-t., Scattering amplitudes, Preprint (2013), arXiv:1308.1697 [hep-th].Google Scholar
Esnault, H. and Viehweg, E., Deligne–Beilinson cohomology, in Beilinson’s conjectures on special values of L-functions, Perspectives in Mathematics, vol. 4 (Academic Press, Boston, MA, 1988), 43–91.CrossRefGoogle Scholar
Griffiths, P. A., On the periods of certain rational integrals. I, II, Ann. of Math. (2) 90 (1969), 460–495; 496–541.CrossRefGoogle Scholar
Griffiths, P. A., A theorem concerning the differential equations satisfied by normal functions associated to algebraic cycles, Amer. J. Math. 101 (1979), 94–131.CrossRefGoogle Scholar
Gunning, R., Lectures on modular forms, Annals of Mathematics Studies, vol. 48 (Princeton University Press, Princeton, NJ, 1962).CrossRefGoogle Scholar
Harder, G. and Schappacher, N., Special values of Hecke L-functions and abelian integrals, Lecture Notes in Mathematics, vol. 1111 (Springer, Berlin, 1985), 17–49.Google Scholar
Henn, J. M., Multiloop integrals in dimensional regularization made simple, Phys. Rev. Lett. 110 (2013), 25160125.CrossRefGoogle ScholarPubMed
Itzykson, C. and Zuber, J. B., Quantum field theory (McGraw-Hill, New York, USA, 1980), 705; International Series in Pure and Applied Physics.Google Scholar
Kerr, M., K 1ind of elliptically fibered K3 surfaces: a tale of two cycles, in Arithmetic and geometry of K3 surfaces and Calabi–Yau threefolds, Fields Institute Communications, vol. 67, eds Laza, R., Schütt, M. and Yui, N. (Springer, New York, 2013), 387–409.CrossRefGoogle Scholar
Kerr, M. and Lewis, J., The Abel–Jacobi map for higher Chow groups, II, Invent. Math. 170 (2007), 355–420.CrossRefGoogle Scholar
Kerr, M., Lewis, J. and Müller-Stach, S., The Abel–Jacobi map for higher Chow groups, Compos. Math. 142 (2006), 374–396.CrossRefGoogle Scholar
Laporta, S. and Remiddi, E., Analytic treatment of the two loop equal mass sunrise graph, Nucl. Phys. B 704 (2005), 349–386.CrossRefGoogle Scholar
Levin, A., Elliptic polylogarithms: an analytic theory, Compositio Math. 106 (1997), 267–282.CrossRefGoogle Scholar
Morrison, D., On K3 surfaces with large Picard number, Invent. Math. 75 (1984), 105–121.CrossRefGoogle Scholar
Morrison, D. and Walcher, J., D-branes and normal functions, Adv. Theor. Math. Phys. 13 (2009), 553–598.CrossRefGoogle Scholar
Müller-Stach, S., Weinzierl, S. and Zayadeh, R., A second-order differential equation for the two-loop sunrise graph with arbitrary masses, Commun. Number Theory Phys. 6 (2012), 203–222.CrossRefGoogle Scholar
Müller-Stach, S., Weinzierl, S. and Zayadeh, R., Picard–Fuchs equations for Feynman integrals, Comm. Math. Phys. 326 (2014), 237–249.CrossRefGoogle Scholar
Ouvry, S., Random Aharonov–Bohm vortices and some exactly solvable families of integrals, J. Stat. Mech. Theory Exp. 1 (2005), P09004.Google Scholar
Peters, C., Top, J. and van der Vlugt, M., The Hasse zeta function of a K3 surface related to the number of words of weight 5 in the Melas codes, J. Reine Angew. Math. 432 (1992), 151–176.Google Scholar
Poincaré, H., Sur les courbes tracées sur les surfaces algébriques, Ann. Sci. Éc. Norm. Supér. (4) 27 (1910), 55–108.CrossRefGoogle Scholar
Schmid, W., Variation of Hodge structure: the singularities of the period mapping, Invent. Math. 22 (1973), 211–319.CrossRefGoogle Scholar
Stein, W. A. et al. , Sage mathematics software (Version 6.2), The Sage Development Team, 2014, http://www.sagemath.org.Google Scholar
Shokurov, S., Holomorphic forms of highest degree on Kuga’s modular varieties, Mat. Sb. (N.S.) 101 (1976), 131–157, 160 (in Russian).Google Scholar
Vanhove, P., The physics and the mixed Hodge structure of Feynman integrals, Proc. Symp. Pure Math. 88 (2014), 161–194.CrossRefGoogle Scholar
Verrill, H., Root lattices and pencils of varieties, J. Math. Kyoto Univ. 36 (1996), 423–446.Google Scholar
Weil, A., Elliptic functions according to Eisenstein and Kronecker, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 88 (Springer, Berlin, Heidelberg, New York, 1976).CrossRefGoogle Scholar
Zagier, D., The Bloch–Wigner–Ramakrishnan polylogarithm function, Math. Ann. 286 (1990), 613–624.CrossRefGoogle Scholar