Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T23:13:08.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Extension theorems for differential forms and Bogomolov–Sommese vanishing on log canonical varieties

Part of: (Co)homology theory Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  11 December 2009

Daniel Greb ,
Stefan Kebekus  and
Sándor J. Kovács
Daniel Greb
Affiliation:
Albert-Ludwigs-Universität Freiburg, Mathematisches Institut, Eckerstrasse 1, 79104 Freiburg im Breisgau, Germany (email: [email protected])
Stefan Kebekus
Affiliation:
Albert-Ludwigs-Universität Freiburg, Mathematisches Institut, Eckerstrasse 1, 79104 Freiburg im Breisgau, Germany (email: [email protected])
Sándor J. Kovács
Affiliation:
University of Washington, Department of Mathematics, Box 354350, Seattle, WA 98195, USA (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

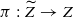Given a normal variety Z, a p-form σ defined on the smooth locus of Z and a resolution of singularities , we study the problem of extending the pull-back π*(σ) over the π-exceptional set 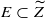. For log canonical pairs and for certain values of p, we show that an extension always exists, possibly with logarithmic poles along E. As a corollary, it is shown that sheaves of reflexive differentials enjoy good pull-back properties. A natural generalization of the well-known Bogomolov–Sommese vanishing theorem to log canonical threefold pairs follows.

Keywords

differential formslog canonicalvanishing theorems

MSC classification

Secondary: 14J17: Singularities 14F17: Vanishing theorems
Type
Research Article
Information
Compositio Mathematica , Volume 146 , Issue 1 , January 2010 , pp. 193 - 219
Copyright
Copyright © Foundation Compositio Mathematica 2009

References

[1]Beltrametti, M. C. and Sommese, A. J., The adjunction theory of complex projective varieties, De Gruyter Expositions in Mathematics, vol. 16 (Walter de Gruyter, Berlin, 1995).CrossRefGoogle Scholar
[2]Brieskorn, E., Rationale Singularitäten komplexer Flächen, Invent. Math. 4 (1967–1968), 336–358.CrossRefGoogle Scholar
[3]Deligne, P., Équations différentielles à points singuliers réguliers, Lecture Notes in Mathematics, vol. 163 (Springer, Berlin, 1970).CrossRefGoogle Scholar
[4]Esnault, H. and Viehweg, E., Lectures on vanishing theorems, DMV Seminar, vol. 20 (Birkhäuser, Basel, 1992).CrossRefGoogle Scholar
[5]Flenner, H., Extendability of differential forms on nonisolated singularities, Invent. Math. 94 (1988), 317–326.CrossRefGoogle Scholar
[6]Hartshorne, R., Local cohomology, A seminar given by A. Grothendieck, Harvard University, Fall, vol. 1961 (Springer, Berlin, 1967).CrossRefGoogle Scholar
[7]Hartshorne, R., Ample subvarieties of algebraic varieties, Notes written in collaboration with C. Musili. Lecture Notes in Mathematics, vol. 156 (Springer, Berlin, 1970).CrossRefGoogle Scholar
[8]Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, New York, 1977).CrossRefGoogle Scholar
[9]Hassett, B. and Kovács, S. J., Reflexive pull-backs and base extension, J. Algebraic Geom. 13 (2004), 233–247.CrossRefGoogle Scholar
[10]Iitaka, S., Algebraic geometry, Graduate Texts in Mathematics, vol. 76 (Springer, New York, 1982); An introduction to birational geometry of algebraic varieties, North-Holland Mathematical Library, vol. 24.Google Scholar
[11]Kaup, W., Infinitesimale Transformationsgruppen komplexer Räume, Math. Ann. 160 (1965), 72–92.CrossRefGoogle Scholar
[12]Kawamata, Y., Matsuda, K. and Matsuki, K., Introduction to the minimal model problem, Algebraic geometry, Sendai, 1985, Advanced Studies in Pure Mathematics, vol. 10 (North-Holland, Amsterdam, 1987), 283–360.CrossRefGoogle Scholar
[13]Kebekus, S. and Kovács, S. J., The structure of surfaces mapping to the moduli stack of canonically polarized varieties, Preprint (2007), arXiv:0707.2054.Google Scholar
[14]Kebekus, S. and Kovács, S. J., Families of canonically polarized varieties over surfaces, Invent. Math. 172 (2008), 657–682; DOI: 10.1007/s00222-008-0128-8.CrossRefGoogle Scholar
[15]Kebekus, S. and Kovács, S. J., The structure of surfaces and threefolds mapping to the moduli stack of canonically polarized varieties, Preprint (2008), arXiv:0812.2305.Google Scholar
[16]Kebekus, S. and Solá Conde, L., Existence of rational curves on algebraic varieties, minimal rational tangents, and applications, in Global aspects of complex geometry (Springer, Berlin, 2006), 359–416.CrossRefGoogle Scholar
[17]Keel, S. and McKernan, J., Rational curves on quasi-projective surfaces, Mem. Amer. Math. Soc. 140 (1999), viii+153.Google Scholar
[18]Kollár, J., Lectures on resolution of singularities, Annals of Mathematics Studies, vol. 166 (Princeton University Press, Princeton, NJ, 2007).Google Scholar
[19]Kollár, J. and Mori, S., Birational geometry of algebraic varieties, Cambridge Tracts in Mathematics, vol. 134 (Cambridge University Press, Cambridge, 1998), with the collaboration of C. H. Clemens and A. Corti, translated from the 1998 Japanese original.CrossRefGoogle Scholar
[20]Langer, A., The Bogomolov–Miyaoka–Yau inequality for log canonical surfaces, J. London Math. Soc. (2) 64 (2001), 327–343.CrossRefGoogle Scholar
[21]Langer, A., Logarithmic orbifold Euler numbers of surfaces with applications, Proc. London Math. Soc. (3) 86 (2003), 358–396.CrossRefGoogle Scholar
[22]Mumford, D., The topology of normal singularities of an algebraic surface and a criterion for simplicity, Publ. Math. Inst. Hautes Études Sci. 9 (1961), 5–22.CrossRefGoogle Scholar
[23]Namikawa, Y., Extension of 2-forms and symplectic varieties, J. Reine Angew. Math. 539 (2001), 123–147.Google Scholar
[24]Okonek, C., Schneider, M. and Spindler, H., Vector bundles on complex projective spaces, Progress in Mathematics, vol. 3 (Birkhäuser, Boston, MA, 1980).Google Scholar
[25]Reid, M., Young person’s guide to canonical singularities, in Algebraic geometry, Bowdoin, 1985 (Brunswick, Maine, 1985), Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 345–414.Google Scholar
[26]Steenbrink, J. H. M., Vanishing theorems on singular spaces, Astérisque 130 (1985), 330–341.Google Scholar
[27]van Straten, D. and Steenbrink, J., Extendability of holomorphic differential forms near isolated hypersurface singularities, Abh. Math. Sem. Univ. Hamburg 55 (1985), 97–110.CrossRefGoogle Scholar
[28]Wahl, J. M., A characterization of quasihomogeneous Gorenstein surface singularities, Compositio Math. 55 (1985), 269–288.Google Scholar