Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T05:09:18.803Z Has data issue: false hasContentIssue false
  • English
  • Français

The essential dimension of congruence covers

Part of: Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  27 October 2021

Benson Farb ,
Mark Kisin  and
Jesse Wolfson
Benson Farb
Affiliation:
Department of Mathematics, University of Chicago, 5734 S. University Avenue, Chicago, IL60637, [email protected]
Mark Kisin
Affiliation:
Department of Mathematics, Harvard University, Science Center Room 325, 1 Oxford Street, Cambridge, MA02138, [email protected]
Jesse Wolfson
Affiliation:
Department of Mathematics, University of California–Irvine, Rowland Hall 340H, Irvine, CA92697, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the algebraic function 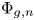$\Phi _{g,n}$ that assigns to a general 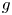$g$-dimensional abelian variety an 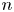$n$-torsion point. A question first posed by Klein asks: What is the minimal 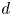$d$ such that, after a rational change of variables, the function 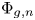$\Phi _{g,n}$ can be written as an algebraic function of 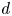$d$ variables? Using techniques from the deformation theory of 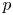$p$-divisible groups and finite flat group schemes, we answer this question by computing the essential dimension and 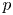$p$-dimension of congruence covers of the moduli space of principally polarized abelian varieties. We apply this result to compute the essential 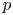$p$-dimension of congruence covers of the moduli space of genus 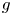$g$ curves, as well as its hyperelliptic locus, and of certain locally symmetric varieties. These results include cases where the locally symmetric variety 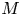$M$ is proper. As far as we know, these are the first examples of nontrivial lower bounds on the essential dimension of an unramified, nonabelian covering of a proper algebraic variety.

Keywords

Shimura varietiesessential dimensionfinite flat group schemes

MSC classification

Primary: 14G35: Modular and Shimura varieties
Secondary: 11G18: Arithmetic aspects of modular and Shimura varieties
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 11 , November 2021 , pp. 2407 - 2432
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The authors are partially supported by NSF grants DMS-1811772 (BF), DMS-1601054 (MK) and DMS-1811846 (JW).

References

Brosnan, P. and Fakhruddin, N., Fixed points, local monodromy, and incompressibility of congruence covers, Preprint (2020), arXiv:2007.01752.Google Scholar
Borovoi, M., Abelianization of the first Galois cohomology of reductive groups, Int. Math. Res. Not. (IMRN) 8 (1996), 401–407.10.1155/S1073792896000268CrossRefGoogle Scholar
Buhler, J. and Reichstein, Z., On the essential dimension of a finite group, Compos. Math. 106 (1997), 159–179.CrossRefGoogle Scholar
Colliot-Thélène, J. L., Exposant et indice d'algèbres simples centrales non ramifiées. (With an appendix by Ofer Gabber.), Enseign. Math. 48 (2002), 127–146.Google Scholar
Deligne, P., Travaux de Shimura, Séminaire Bourbaki, 23ème année (1970/71), Exp. No. 389, Lecture Notes in Mathematics, vol. 244 (Springer, Berlin, 1971), 123–165.10.1007/BFb0058700CrossRefGoogle Scholar
Deligne, P., Variétés de Shimura: interprétation modulaire, et techniques de construction de modèles canoniques, in Automorphic forms, representations and $L$-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 2 (American Mathematical Society, Providence, RI, 1979), 247–289.Google Scholar
Deligne, P. and Mumford, D., The irreducibility of the space of curves of given genus, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 75–109.CrossRefGoogle Scholar
Dickson, L. E., Representations of the general symmetric group as linear groups in finite and infinite fields, Trans. Amer. Math. Soc. 9 (1908), 121–148.10.1090/S0002-9947-1908-1500805-8CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique: I–IV, Publ. Math. Inst. Hautes Études Sci. 4, 8, 11, 17, 20, 24, 32 (1960–1967).Google Scholar
Faber, C. and van der Geer, G., Complete subvarieties of moduli spaces and the Prym map, J. Reine Angew. Math. 573 (2004), 117–137.Google Scholar
Farb, B. and Dennis, R. K., Noncommutative algebra, Graduate Texts in Mathematics, vol. 144 (Springer, New York, 1993).CrossRefGoogle Scholar
Glass, D. and Pries, R., Hyperelliptic curves with prescribed $p$-torsion, Manuscripta Math. 117 (2005), 299–317.10.1007/s00229-005-0559-0CrossRefGoogle Scholar
Harder, G. and Borel, A., Existence of discrete cocompact subgroups of reductive groups over local fields, J. Reine Angew. Math. 298 (1978), 53–64.Google Scholar
Hilbert, D., Uber die Gleichung neunten Grades, Math. Ann. 97 (1927), 43–250.10.1007/BF01447867CrossRefGoogle Scholar
Jordan, C., Traité des substitutions (Gauthier-Villars, Paris, 1870).Google Scholar
Katz, N., Serre-Tate local moduli, in Algebraic surfaces (Orsay, 1976–78) (Springer, Berlin, 1981).Google Scholar
Kim, W. and Pera, K. M., 2-adic integral canonical models, Forum Math. Sigma 4 (2016), e28.10.1017/fms.2016.23CrossRefGoogle Scholar
Kisin, M., Integral models for Shimura varieties of abelian type, J. Amer. Math. Soc. 23 (2010), 967–1012.10.1090/S0894-0347-10-00667-3CrossRefGoogle Scholar
Klein, F., Vorlesungen über das Ikosaeder und die Auflösung der Gleichungen vom fünften Grade (Lectures on the Icosahedron and the Solution of the Equation of the Fifth Degree) (Teubner, Leipzig, 1884).Google Scholar
Klein, F., Sur la resolution, par les fonctions hyperelliptiques de l'equation du vingt-septieme degre, de laquelle depend la determination des vingt-sept droites d'une surface cubique, J. Math. Pures Appl. 4 (1888), 169–176.Google Scholar
Klein, F., Zur Theorie der Abel'schen Functionen, Math. Ann. 36 (1890), 1–83.CrossRefGoogle Scholar
Knight, H., The essential $p$-dimension of quasi-simple finite groups of Lie type, Preprint (2021), arXiv:2109.02698.Google Scholar
Kottwitz, R. E., Stable trace formula: elliptic singular terms, Math. Ann. 275 (1986), 365–399.10.1007/BF01458611CrossRefGoogle Scholar
Kronecker, L., Ueber die Gleichungen fünften g rades, J. Reine Angew. Math. 59 (1861), 306–310.Google Scholar
Landesman, A., The Torelli map restricted to the hyperelliptic locus, Preprint (2019), arXiv:1911.02084.Google Scholar
Matsusaka, T., On a theorem of Torelli, Amer. J. Math. 80 (1958), 784–800.CrossRefGoogle Scholar
McMullen, C., Braids and Hodge theory, Math. Ann. 355 (2013), 893–946.10.1007/s00208-012-0804-2CrossRefGoogle Scholar
Meyer, A. and Reichstein, Z., The essential dimension of the normalizer of a maximal torus in the projective linear group, Algebra Number Theory 3 (2009), 467–487.10.2140/ant.2009.3.467CrossRefGoogle Scholar
Poonen, B., Varieties without extra automorphisms. II. Hyperelliptic curves, Math. Res. Lett. 7 (2000), 77–82.CrossRefGoogle Scholar
Oort, F. and Steenbrink, J., The local Torelli problem for algebraic curves, in Journées de Géometrie Algébrique d'Angers, Juillet 1979/Algebraic Geometry, Angers, 1979 (Sijthoff & Noordhoff, Alphen aan den Rijn, 1980), 157–204.Google Scholar
Raynaud, M. and Gruson, L., Critères de platitude et de projectivité. Techniques de ‘platification’ d'un module, Invent. Math. 13 (1971), 1–89.CrossRefGoogle Scholar
Reichstein, Z., Essential dimension, in Proceedings of the International Congress of Mathematicians (ICM2010) (Hindustan Book Agency, 2011).10.1142/9789814324359_0045CrossRefGoogle Scholar
Reichstein, Z. and Youssin, B., Essential dimensions of algebraic groups and a resolution theorem for $G$-varieties, Canad. J. Math. 52 (2000), 1018–1056; with an appendix by János Kollár and Endre Szabó.CrossRefGoogle Scholar
Grothendieck, A., Revêtements étales et groupe fondamental (SGA1), in Séminaire de géométrie algébrique, vol. 1960/61 (Institut des Hautes Études Scientifiques, Paris, 1963).Google Scholar
Grothendieck, A., Séminaire de Géométrie Algébrique du Bois-Marie, 1962 – Cohomologie locale des faisceaux cohérents et théorèmes de Lefschetz locaux et globaux (SGA 2), Advanced Studies in Pure Mathematics, vol. 2 (North-Holland/Masson & Cie, Amsterdam/Éditeur, Paris, 1968).Google Scholar
Demazure, M. and Grothendieck, A., Schémas en groupes (SGA3). Fasc. 7: Exposés 23 à 26, in Séminaire de géométrie algébrique de l'Institut des Hautes Études Scientifiques, vol. 1963/64 (Institut des Hautes Études Scientifiques, Paris, 1965/1966).Google Scholar
Tschebotaröw, N. G., Die Probleme der modernen Galoisschen Theorie, Comment. Math. Helv. 6 (1934), 235–283.10.1007/BF01297335CrossRefGoogle Scholar
Saltman, David J., Generic Galois extensions and problems in field theory, Adv. Math. 43 (1982), 250–283.10.1016/0001-8708(82)90036-6CrossRefGoogle Scholar
Wortmann, D., The $\mu$-ordinary locus for Shimura varieties of Hodge type, Preprint (2013), arXiv:1310.6444.Google Scholar