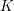Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
PECHENIK, OLIVER
and
YONG, ALEXANDER
2017.
EQUIVARIANT -THEORY OF GRASSMANNIANS.
Forum of Mathematics, Pi,
Vol. 5,
Issue. ,
Kaliszewski, Ryan
and
Morse, Jennifer
2019.
Colorful combinatorics and Macdonald polynomials.
European Journal of Combinatorics,
Vol. 81,
Issue. ,
p.
354.
Wheeler, Michael
and
Zinn-Justin, Paul
2019.
Littlewood–Richardson coefficients for Grothendieck polynomials from integrability.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 757,
p.
159.
Gillespie, Maria
2019.
Recent Trends in Algebraic Combinatorics.
Vol. 16,
Issue. ,
p.
115.
Pak, Igor
2024.
Open Problems in Algebraic Combinatorics.
Vol. 110,
Issue. ,
p.
191.
Fan, Neil J.Y.
Guo, Peter L.
and
Xiong, Rui
2025.
Bumpless pipe dreams meet puzzles.
Advances in Mathematics,
Vol. 463,
Issue. ,
p.
110113.