Published online by Cambridge University Press: 13 March 2017
A log symplectic manifold is a complex manifold equipped with a complex symplectic form that has simple poles on a hypersurface. The possible singularities of such a hypersurface are heavily constrained. We introduce the notion of an elliptic point of a log symplectic structure, which is a singular point at which a natural transversality condition involving the modular vector field is satisfied, and we prove a local normal form for such points that involves the simple elliptic surface singularities 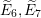 $\widetilde{E}_{6},\widetilde{E}_{7}$ and
$\widetilde{E}_{6},\widetilde{E}_{7}$ and 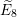 $\widetilde{E}_{8}$. Our main application is to the classification of Poisson brackets on Fano fourfolds. For example, we show that Feigin and Odesskii’s Poisson structures of type
$\widetilde{E}_{8}$. Our main application is to the classification of Poisson brackets on Fano fourfolds. For example, we show that Feigin and Odesskii’s Poisson structures of type 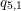 $q_{5,1}$ are the only log symplectic structures on projective four-space whose singular points are all elliptic.
$q_{5,1}$ are the only log symplectic structures on projective four-space whose singular points are all elliptic.