Duality for relative logarithmic de Rham–Witt sheaves and wildly ramified class field theory over finite fields

Abstract

In order to study 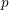$p$-adic étale cohomology of an open subvariety 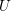$U$ of a smooth proper variety 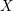$X$ over a perfect field of characteristic 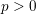$p>0$, we introduce new 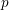$p$-primary torsion sheaves. It is a modification of the logarithmic de Rham–Witt sheaves of 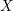$X$ depending on effective divisors 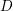$D$ supported in 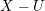$X-U$. Then we establish a perfect duality between cohomology groups of the logarithmic de Rham–Witt cohomology of 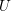$U$ and an inverse limit of those of the mentioned modified sheaves. Over a finite field, the duality can be used to study wildly ramified class field theory for the open subvariety 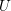$U$.

Introduction

Let $k$ be a perfect field of characteristic $p>0$ and let $X$ be a smooth proper variety of dimension $d$ over $k$ . The logarithmic de Rham–Witt sheaves $W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r}$ are defined as the subsheaves of the de Rham–Witt sheaves $W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}$ , which are étale locally generated by sections $d\log [x_{1}]_{m}\wedge \cdots \wedge d\log [x_{r}]_{m}$ with $x_{\unicode[STIX]{x1D708}}\in {\mathcal{O}}_{X}^{\times }$ for all $\unicode[STIX]{x1D708}$ [Ill79]. By the Gersten resolution [Ros96, Ker10, GS88] and the Bloch–Gabber–Kato theorem [BK86], the $d\log$ map induces an isomorphism of étale sheaves

(1) $$\begin{eqnarray}\displaystyle d\log [-]:{\mathcal{K}}_{r,X}^{M}/p^{m}\xrightarrow[{}]{\cong }W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r}\;;\;\{x_{1},\ldots ,x_{r}\}\mapsto d\log [x_{1}]_{m}\wedge \cdots \wedge d\log [x_{r}]_{m}, & & \displaystyle\end{eqnarray}$$

where ${\mathcal{K}}_{r,X}^{M}$ is the sheaf of Milnor $K$ -groups. It is conceived as a $p$ -adic analogue of the $\ell$ -adic sheaf $\unicode[STIX]{x1D707}_{\ell ^{m}}^{\otimes r}$ with $\ell \neq p$ . If $k$ is a finite field, there is a non-degenerate pairing of finite groups due to Milne [Mil86]:

$$\begin{eqnarray}H^{i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r})\times H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d-r})\rightarrow H^{d+1}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d})\xrightarrow[{}]{\text{Tr}}\mathbb{Z}/p^{m}\mathbb{Z}.\end{eqnarray}$$

It induces a natural isomorphism

$$\begin{eqnarray}H^{d}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d})\cong H^{1}(X,\mathbb{Z}/p^{m}\mathbb{Z})^{\vee }\cong \unicode[STIX]{x1D70B}_{1}^{ab}(X)/p^{m},\end{eqnarray}$$

where $A^{\vee }$ is the Pontryagin dual of a discrete abelian group and $\unicode[STIX]{x1D70B}_{1}^{ab}(X)$ is the maximal abelian quotient of Grothendieck’s étale fundamental group of $X$ . This gives a description of $\unicode[STIX]{x1D70B}_{1}^{ab}(X)/p^{m}$ in terms of étale cohomology with $p$ -adic coefficient. For $\ell$ -adic étale cohomology, we also have a non-degenerate pairing of finite groups for a smooth non-proper variety $U$ of dimension $d$ over a finite field $k$ [SGA4½, Sai89]

$$\begin{eqnarray}H^{i}(U,\mathbb{Z}/\ell ^{m}(j))\times H_{c}^{2d+1-i}(U,\mathbb{Z}/\ell ^{m}(d-j))\rightarrow H_{c}^{2d+1}(U,\mathbb{Z}/\ell ^{m}(d))\cong \mathbb{Z}/\ell ^{m}\mathbb{Z},\end{eqnarray}$$

which can be used to describe $\unicode[STIX]{x1D70B}_{1}^{ab}(U)/\ell ^{m}$ by $\ell$ -adic étale cohomology:

$$\begin{eqnarray}H_{c}^{2d}(U,\mathbb{Z}/\ell ^{m}(d))\cong H^{1}(U,\mathbb{Z}/\ell ^{m})^{\vee }\cong \unicode[STIX]{x1D70B}_{1}^{ab}(U)/\ell ^{m}.\end{eqnarray}$$

In the $p$ -adic setting there is no obvious analogue of étale cohomology with compact support for logarithmic de Rham–Witt sheaves.

In this paper, we propose a new approach. Let $X$ be a proper smooth variety over a perfect field $k$ as before, and let $j:U{\hookrightarrow}X$ be the complement of an effective divisor $D$ such that Supp( $D$ ) has simple normal crossings. We introduce new $p$ -primary torsion sheaves $W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ (see Definition 1.1.1), which we call relative logarithmic de Rham–Witt sheaves. It is defined as the subsheaf of the de Rham–Witt sheaf $W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}$ which is étale locally generated by sections $d\log [x_{1}]_{m}\wedge \ldots \wedge d\log [x_{r}]_{m}$ with $x_{1}\in \text{Ker}({\mathcal{O}}_{X}^{\times }\rightarrow {\mathcal{O}}_{D}^{\times })$ , and $x_{\unicode[STIX]{x1D708}}\in j_{\ast }{\mathcal{O}}_{U}^{\times }$ for all $\unicode[STIX]{x1D708}$ . As in the classical situation, we have the following theorem.

Theorem 1 (see Theorem 1.1.5).

The map $d\log$ induces an isomorphism

(2) $$\begin{eqnarray}\displaystyle d\log [-]:{\mathcal{K}}_{r,X|D}^{M}/(p^{m}{\mathcal{K}}_{r,X}^{M}\cap {\mathcal{K}}_{r,X|D}^{M}) & \xrightarrow[{}]{\cong } & \displaystyle W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\nonumber\\ \displaystyle \{x_{1},\ldots ,x_{r}\} & \mapsto & \displaystyle d\log [x_{1}]_{m}\wedge \cdots \wedge d\log [x_{r}]_{m}.\end{eqnarray}$$

Here ${\mathcal{K}}_{r,X|D}^{M}$ is the sheaf of relative Milnor $K$ -groups which has been studied by one of the authors (Saito) and Rülling in [RS18].

If $D_{1}\geqslant D_{2}$ , we have inclusions (see Proposition 1.1.4)

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{1},\log }^{r}\subseteq W_{m}\unicode[STIX]{x1D6FA}_{X|D_{2},\log }^{r}\subseteq W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r},\end{eqnarray}$$

and thus obtain a pro-system of $\mathbb{Z}/p^{m}\mathbb{Z}$ -sheaves “ $\mathop{\varprojlim }\nolimits_{D}$ ” $W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ , where $D$ runs over the set of all effective divisors with $\text{Supp}(D)\subset X-U$ .

In case $m=1$ these sheaves are related to sheaves of differential forms by the exact sequence (see Theorem 1.2.1)

(3) $$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\rightarrow \unicode[STIX]{x1D6FA}_{X|D}^{r}\xrightarrow[{}]{1-C^{-1}}\unicode[STIX]{x1D6FA}_{X|D}^{r}/d\unicode[STIX]{x1D6FA}_{X|D}^{r-1}\rightarrow 0,\end{eqnarray}$$

where $\unicode[STIX]{x1D6FA}_{X|D}^{r}=\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{X}(-D)$ and $C^{-1}$ is the inverse Cartier morphism. In order to extend the above exact sequence to the case $m>1$ , we need introduce the filtered relative de Rham–Witt complex $W_{m}\unicode[STIX]{x1D6FA}_{X|D}^{\bullet }$ for which we have $W_{1}\unicode[STIX]{x1D6FA}_{X|D}^{\bullet }=\unicode[STIX]{x1D6FA}_{X|D}^{\bullet }$ (see § 2.3 and Theorem 2.3.1). Its construction uses the de Rham–Witt complexes in log geometry [HK94], which can be seen as the higher analogue of $\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)$ .

Using the generalization of (3) to the case $m>1$ , we can define a pairing between $W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r}$ and the pro-system “ $\mathop{\varprojlim }\nolimits_{D}$ ” $W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}$ and obtain the following theorem.

Theorem 2 (see Theorem 4.1.4).

Let $X$ , $D$ and $U$ be as above and assume that $k$ is finite. Then the groups $H^{j}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r})$ are finite and there are natural perfect pairings of topological abelian groups

$$\begin{eqnarray}H^{i}(U,W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r})\times \underset{D}{\varprojlim }\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})\rightarrow H^{d+1}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d})\xrightarrow[{}]{\text{Tr}}\mathbb{Z}/p^{m}\mathbb{Z},\end{eqnarray}$$

where the first group is endowed with discrete topology, and the second is endowed with profinite topology.

From the case $i=1$ and $r=0$ of the above theorem, we get a natural isomorphism

$$\begin{eqnarray}\underset{D}{\varprojlim }\,H^{d}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d})\xrightarrow[{}]{\cong }H^{1}(U,\mathbb{Z}/p^{m}\mathbb{Z})^{\vee }\cong \unicode[STIX]{x1D70B}_{1}^{\text{ab}}(U)/p^{m},\end{eqnarray}$$

which gives rise to a series of quotients $\unicode[STIX]{x1D70B}_{1}^{\text{ab}}(X,D)/p^{m}$ of $\unicode[STIX]{x1D70B}_{1}^{\text{ab}}(U)/p^{m}$ using the inverse limit. It is thought of as classifying abelian étale covering of $U$ whose degree divides $p^{m}$ and ramification is bounded by the divisor $D$ .

One of the authors (Zhao) [Zha16] has proved a similar duality theorem for a projective semi-stable scheme over an equi-characteristic discrete valuation ring $k[[t]]$ with $k$ finite.

When the base field $k$ is prefect but not necessarily finite, we follow the method of Milne [Mil86] and work in the category $\mathscr{S}(p^{m})$ of $\mathbb{Z}/p^{m}\mathbb{Z}$ -sheaves on perfect étale site $(\mathit{Pf}/k)_{\acute{\text{e}}\text{t}}$ (see § 5.1). Let $D^{b}(\mathscr{S}(p^{m}))$ be the derived category of bounded complexes in $\mathscr{S}(p^{m})$ . We then get from $X,\;D$ objects of $D^{b}(\mathscr{S}(p^{m}))$ :

$$\begin{eqnarray}R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}\quad \text{and}\quad R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r},\end{eqnarray}$$

where $\unicode[STIX]{x1D70B}:X\rightarrow S=\text{Spec}(k)$ is the structure morphism and $j:U\rightarrow X$ is the open immersion. Then our duality theorem reads as follows.

Theorem 3 (see Theorem 5.2.1).

There is a natural isomorphism in $D^{b}(\mathscr{S}(p^{m}))$ :

$$\begin{eqnarray}R\,\underset{D}{\varprojlim }\,R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}\xrightarrow[{}]{\cong }R{\mathcal{H}}om_{D^{b}(\mathscr{S}(p^{m}))}(R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r},\mathbb{Z}/p^{m}\mathbb{Z})[-d],\end{eqnarray}$$

where $R\,\mathop{\varprojlim }\nolimits_{D}$ denotes the homotopy limit over effective Cartier divisors supported on $X-U$ .

The paper is organized as follows.

In § 1, we study the two important results on the relative logarithmic de Rham–Witt sheaves: the first one is a computation of the kernel of the restriction map $R^{m-1}:W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\rightarrow W_{1}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ ; the second is the exact sequence (3).

In order to define the desired pairing, we introduce filtered de Rham–Witt complexes in § 2, and study the behavior of Frobenius and Verschiebung morphisms on these complexes.

Using two-term complexes, we define the pairing in § 3 and prove its perfectness when the base field $k$ is finite in § 4. The last § 5 is on the duality over a general perfect field.

1 Relative logarithmic de Rham–Witt sheaves

Let $X$ be a smooth proper variety of dimension $d$ over a perfect field $k$ of characteristic $p>0$ , let $D$ be an effective divisor such that $\text{Supp}(D)$ is a simple normal crossing divisor on $X$ , and let $j:U:=X-D{\hookrightarrow}X$ be the complement of $D$ .

1.1 Basic properties

Definition 1.1.1. For $r\in \mathbb{N}$ let

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\subset j_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r}\end{eqnarray}$$

be the subsheaf generated étale locally by sections

$$\begin{eqnarray}d\log [x_{1}]_{m}\wedge \cdots \wedge d\log [x_{r}]_{m}\quad \text{with}~x_{1}\in \text{Ker}({\mathcal{O}}_{X}^{\times }\rightarrow {\mathcal{O}}_{D}^{\times }),x_{\unicode[STIX]{x1D708}}\in j_{\ast }{\mathcal{O}}_{U}^{\times }~\text{for all}~\unicode[STIX]{x1D708}.\end{eqnarray}$$

For $r\in \mathbb{N}$ let ${\mathcal{K}}_{r,X}^{M}$ be the $r$ th Milnor $K$ -sheaf on $X_{\acute{\text{e}}\text{t}}$ given by

$$\begin{eqnarray}V\mapsto \text{Ker}\biggl(\underset{\unicode[STIX]{x1D702}\in V^{(0)}}{\bigoplus }K_{r}^{M}(k(\unicode[STIX]{x1D702}))\xrightarrow[{}]{\oplus \unicode[STIX]{x2202}_{x}}\underset{x\in V^{(1)}}{\bigoplus }K_{r-1}^{M}(k(x))\biggr)\quad \text{for an }\acute{\text{e}}\text{tale}~V\rightarrow X,\end{eqnarray}$$

where $V^{(i)}$ is the set of points of codimension $i$ in $V$ , for $i=0,1$ , and $\unicode[STIX]{x2202}_{x}:K_{r}^{M}(k(\unicode[STIX]{x1D702}))\rightarrow K_{r}^{M}(k(x))$ is the tame symbol from [BT73, § 4]. By [Ker10, Proposition 10(8) and Theorem 13], ${\mathcal{K}}_{r,X}^{M}$ is étale locally generated by symbols $\{x_{1},\ldots ,x_{r}\}$ with $x_{i}\in {\mathcal{O}}_{X,x}^{\times }$ . We have a natural isomorphism of étale sheaves

(1.1.1) $$\begin{eqnarray}\displaystyle d\log [-]:{\mathcal{K}}_{r,X}^{M}/p^{m} & \xrightarrow[{}]{\cong } & \displaystyle W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r}\nonumber\\ \displaystyle \{x_{1},\ldots ,x_{r}\} & \mapsto & \displaystyle d\log [x_{1}]_{m}\wedge \cdots \wedge d\log [x_{r}]_{m}.\end{eqnarray}$$

This follows from the Gersten resolutions of $\unicode[STIX]{x1D716}_{\ast }{\mathcal{K}}_{r,X}^{M}$ and $\unicode[STIX]{x1D716}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r}$ from [Ros96] and [GS88] together with the Bloch–Gabber–Kato theorem [BK86], where $\unicode[STIX]{x1D716}:X_{\acute{\text{e}}\text{t}}\rightarrow X_{\text{Zar}}$ is the map of sites.

Definition 1.1.2 [RS18, Definition 2.4].

For $r\in \mathbb{N}$ , we define the relative Milnor $K$ -sheaf ${\mathcal{K}}_{r,X|D}^{M}$ to be image of the map

$$\begin{eqnarray}\text{Ker}({\mathcal{O}}_{X}^{\times }\rightarrow {\mathcal{O}}_{D}^{\times })\otimes _{\mathbb{ Z}}j_{\ast }{\mathcal{K}}_{r-1,U}^{M}\rightarrow j_{\ast }{\mathcal{K}}_{r,U}^{M};~x\otimes \{x_{1},\ldots ,x_{r-1}\}\mapsto \{x,x_{1},\ldots ,x_{r}\}.\end{eqnarray}$$

Using some symbol calculations, we get the following proposition.

Proposition 1.1.3 [RS18, Corollary 2.9].

Let $D_{1},D_{2}$ be two effective divisors on $X$ whose supports are simple normal crossing divisors. Assume $D_{1}\leqslant D_{2}$ . Then we have the inclusions of sheaves

$$\begin{eqnarray}{\mathcal{K}}_{r,X|D_{2}}^{M}\subset {\mathcal{K}}_{r,X|D_{1}}^{M}\subset {\mathcal{K}}_{r,X}^{M}.\end{eqnarray}$$

Corollary 1.1.4. Under the assumption of Proposition 1.1.3, we have inclusions

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{2},\log }^{r}\subset W_{m}\unicode[STIX]{x1D6FA}_{X|D_{1},\log }^{r}\subset W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r}.\end{eqnarray}$$

Proof. This follows from the fact that the sheaf $W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ is the image of ${\mathcal{K}}_{r,X|D}^{M}$ under the map $d\log [-]$ .◻

The isomorphism (1.1.1) also has the following relative version.

Theorem 1.1.5. The $d\log$ map induces an isomorphism of étale sheaves

(1.1.2) $$\begin{eqnarray}\displaystyle d\log [-]:{\mathcal{K}}_{r,X|D}^{M}/(p^{m}{\mathcal{K}}_{r,X}^{M}\cap {\mathcal{K}}_{r,X|D}^{M}) & \xrightarrow[{}]{\cong } & \displaystyle W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\nonumber\\ \displaystyle \{x_{1},\ldots ,x_{r}\} & \mapsto & \displaystyle d\log [x_{1}]_{m}\wedge \cdots \wedge d\log [x_{r}]_{m}.\end{eqnarray}$$

Proof. The assertion follows directly by the following commutative diagram.

In the rest of this section, we will prove two fundamental results for the relative logarithmic de Rham–Witt sheaves.

Theorem 1.1.6. Write $D=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}n_{\unicode[STIX]{x1D706}}D_{\unicode[STIX]{x1D706}}$ , where $D_{\unicode[STIX]{x1D706}}$ ( $\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}$ ) are irreducible components of $D$ . Then we have an exact sequence

$$\begin{eqnarray}0\rightarrow W_{m-1}\unicode[STIX]{x1D6FA}_{X|[D/p],\log }^{r}\xrightarrow[{}]{\text{}\underline{p}}W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\rightarrow W_{1}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\rightarrow 0,\end{eqnarray}$$

where $[D/p]=\sum _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}[n_{\unicode[STIX]{x1D706}}/p]D_{\unicode[STIX]{x1D706}}$ with $[n/p]=\min \{n^{\prime }\in \mathbb{Z}\mid pn^{\prime }\geqslant n\}.$

Proof. The claim follows from Theorem 1.1.7 below by the isomorphism (1.1.2). ◻

Let $R$ be the henselization of a local ring of a smooth scheme over a field $k$ of characteristic $p>0$ . Let $(T_{1},\ldots ,T_{d})\subset R$ be a part of a system of regular parameters and put $T=T_{1}\cdots T_{d}$ . We endow $\mathbb{N}^{d}$ with a semi-order by

$$\begin{eqnarray}(n_{1},\ldots ,n_{d})\leqslant (n_{1}^{\prime },\ldots ,n_{d}^{\prime })\quad \text{if}\;n_{i}\leqslant n_{i}^{\prime }~\text{for all}~i\end{eqnarray}$$

and put

$$\begin{eqnarray}\text{}\underline{1}=(1,\ldots ,1).\end{eqnarray}$$

Following [BK86, § 4], we define $U^{\text{}\underline{n}}K_{r}^{M}(R)\subset K_{r}^{M}(R)$ for $\text{}\underline{n}=(n_{1},\ldots ,n_{d})\in \mathbb{N}^{d}$ as the subgroup generated by symbols

$$\begin{eqnarray}\{x_{1},\ldots ,x_{r}\}\text{with }x_{1}\in 1+T_{1}^{n_{1}}\cdots T_{d}^{n_{d}}R,\;x_{i}\in R[1/T]^{\times }\quad (2\leqslant i\leqslant d).\end{eqnarray}$$

(Here having the injectivity of $K_{r}^{M}(R)\rightarrow K_{r}^{M}(K)$ with the quotient field $K$ of $R$ , the above symbols are considered in $K_{r}^{M}(K)$ .) For an integer $m>0$ , put

$$\begin{eqnarray}U^{\text{}\underline{n}}k_{r}^{M}(R)_{m}=\operatorname{Image}(U^{\text{}\underline{n}}K_{r}^{M}(R)\rightarrow K_{r}^{M}(R)/p^{m}).\end{eqnarray}$$

Theorem 1.1.7. We have the following exact sequence:

$$\begin{eqnarray}0\rightarrow U^{[\text{}\underline{n}/p]}k_{r}^{M}(R)_{m-1}\xrightarrow[{}]{p}U^{\text{}\underline{n}}k_{r}^{M}(R)_{m}\rightarrow U^{\text{}\underline{n}}k_{r}^{M}(R)_{1}\rightarrow 0,\end{eqnarray}$$

where $[\text{}\underline{n}/p]=\min \{\text{}\underline{\unicode[STIX]{x1D708}}\in \mathbb{N}^{d}|\;p\text{}\underline{\unicode[STIX]{x1D708}}\geqslant \text{}\underline{n}\}\in \mathbb{N}^{d}$ .

For the proof we compute

$$\begin{eqnarray}gr^{\text{}\underline{n},i}k_{r}^{M}(R)_{m}=U^{\text{}\underline{n}}k_{r}^{M}(R)_{m}/U^{\text{}\underline{n}+\unicode[STIX]{x1D6FF}_{i}}k_{r}^{M}(R)_{m}\quad \text{with}\;\unicode[STIX]{x1D6FF}_{i}=(0,\ldots ,\overset{\underset{\vee }{i}}{1},\ldots ,0).\end{eqnarray}$$

We need some preliminaries. For $\text{}\underline{n}\in \mathbb{N}^{d}$ and $1\leqslant i\leqslant d$ and an integer $q\geqslant 1$ put

$$\begin{eqnarray}\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q}=I^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}(\log T)\otimes _{R}R_{i}\quad \text{with}\;R_{i}=R/(T_{i}),\end{eqnarray}$$

where $I^{\text{}\underline{n}}=(T_{1}^{n_{1}}\cdots T_{d}^{n_{d}})\subset R$ and $\unicode[STIX]{x1D6FA}_{R}^{q}(\log T)$ is the sheaf of (absolute) differential $q$ -forms of $R$ with logarithmic poles along $T=0$ . It is easy to check the exterior derivative induces

$$\begin{eqnarray}d^{q}:\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q}\rightarrow \unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q+1}.\end{eqnarray}$$

Put

$$\begin{eqnarray}Z_{\text{}\underline{n},i}^{q}=\text{Ker}(\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q}\xrightarrow[{}]{d^{q}}\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q+1}),\quad B_{\text{}\underline{n},i}^{q}=\operatorname{Image}(\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q-1}\xrightarrow[{}]{d^{q-1}}\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q}).\end{eqnarray}$$

We can easily check the following.

Lemma 1.1.8 [RS18, Theorem 2.16].

Let the notation be as above. Then the inverse Cartier morphism

$$\begin{eqnarray}C^{-1}:\unicode[STIX]{x1D6FA}_{R}^{q}\rightarrow \unicode[STIX]{x1D6FA}_{R}^{q}/d\unicode[STIX]{x1D6FA}_{R}^{q-1}\end{eqnarray}$$

induces an isomorphism

$$\begin{eqnarray}C_{\text{}\underline{n},i}^{-1}:\unicode[STIX]{x1D714}_{[\text{}\underline{n}/p],i}^{q}\xrightarrow[{}]{\cong }Z_{\text{}\underline{n},i}^{q}/B_{\text{}\underline{n},i}^{q}.\end{eqnarray}$$

We define subgroups

$$\begin{eqnarray}B_{\text{}\underline{n},i}^{q}=B_{1|\text{}\underline{n},i}^{q}\subset B_{2|\text{}\underline{n},i}^{q}\subset \cdots \subset Z_{2|\text{}\underline{n},i}^{q}\subset Z_{1|\text{}\underline{n},i}^{q}=Z_{\text{}\underline{n},i}^{q}\subset \unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{q},\end{eqnarray}$$

by the inductive formulae

$$\begin{eqnarray}B_{s|[\text{}\underline{n}/p],i}^{q}\xrightarrow[{C_{\text{}\underline{n},i}^{-1}}]{\simeq }B_{s+1|\text{}\underline{n},i}^{q}/B_{\text{}\underline{n},i}^{q},\quad Z_{s|[\text{}\underline{n}/p],i}^{q}\xrightarrow[{C_{\text{}\underline{n},i}^{-1}}]{\simeq }Z_{s+1|\text{}\underline{n},i}^{q}/B_{\text{}\underline{n},i}^{q}.\end{eqnarray}$$

Proposition 1.1.9. Fix $\text{}\underline{n}=(n_{1},\ldots ,n_{d})\in \mathbb{N}^{d}$ and $1\leqslant i\leqslant d$ .

1. (1) There is a natural map

   $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\text{}\underline{n},i}:\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{r-1}\rightarrow gr^{\text{}\underline{n},i}k_{r}^{M}(R)_{m}\end{eqnarray}$$
   such that for $a\in R$ , $b_{2},\ldots ,b_{d}\in R[1/T]^{\times }$ ,
   $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\text{}\underline{n},i}\bigg(a(T_{1}^{n_{1}}\cdots T_{d}^{n_{d}})\displaystyle \frac{db_{2}}{b_{2}}\wedge \cdots \wedge \displaystyle \frac{db_{r}}{b_{r}}\bigg)=\{1+aT_{1}^{n_{1}}\cdots T_{d}^{n_{d}},b_{2},\ldots ,b_{r}\}\in U^{\text{}\underline{n}}K_{r}^{M}(R).\end{eqnarray}$$

2. (2) Write $n_{i}=p^{s}\cdot n^{\prime }$ with $p\not |n^{\prime }$ . If $m>s$ , $\unicode[STIX]{x1D70C}_{\text{}\underline{n},i}$ induces an isomorphism

   $$\begin{eqnarray}\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{r-1}/B_{s|\text{}\underline{n},i}^{r-1}\xrightarrow[{}]{\cong }gr^{\text{}\underline{n},i}k_{r}^{M}(R)_{m}.\end{eqnarray}$$
   If $m\leqslant s$ , $\unicode[STIX]{x1D70C}_{\text{}\underline{n},i}$ induces an isomorphism
   $$\begin{eqnarray}\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{r-1}/Z_{m|\text{}\underline{n},i}^{r-1}\xrightarrow[{}]{\cong }gr^{\text{}\underline{n},i}k_{r}^{M}(R)_{m}.\end{eqnarray}$$

Proof. The existence of $\unicode[STIX]{x1D70C}_{\text{}\underline{n},i}$ together with the fact that it induces the surjective maps as in (2) is shown by the same argument as [BK86, (4.5) and (4.6)]. Note that $\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{r-1}/B_{s|\text{}\underline{n},i}^{r-1}$ and $\unicode[STIX]{x1D714}_{\text{}\underline{n},i}^{r-1}/Z_{m|\text{}\underline{n},i}^{r-1}$ are free $R_{i}^{p^{e}}$ -modules, for some $e\gg 0$ . By localization, the injectivity of the maps is reduced to the case $R$ is a discrete valuation ring, which has been treated in [BK86, (4.8)].◻

Now we prove Theorem 1.1.7. It is easy to see that we have a complex as in the theorem. Its exactness on the left follows from the fact that $K_{r}^{M}(R)$ is $p$ -torsion free (cf. [GL00, Theorem 8.1] and [Ros96, Theorem 6.1]). It remains to show the exactness in the middle. For this it suffices to show the injectivity of the map induced by multiplication by $p$ :

$$\begin{eqnarray}K_{r}^{M}(R)/U^{[\text{}\underline{n}/p]}K_{r}^{M}(R)+p^{m-1}K_{r}^{M}(R)\xrightarrow[{}]{p}K_{r}^{M}(R)/U^{\text{}\underline{n}}K_{r}^{M}(R)+p^{m}K_{r}^{M}(R).\end{eqnarray}$$

This follows from the following claims.

Claim 1.1.10. The multiplication by $p$ induces an injective map:

$$\begin{eqnarray}K_{r}^{M}(R)/U^{\text{}\underline{1}}K_{r}^{M}(R)+p^{m-1}K_{r}^{M}(R)\rightarrow K_{r}^{M}(R)/U^{\text{}\underline{1}}K_{r}^{M}(R)+p^{m}K_{r}^{M}(R).\end{eqnarray}$$

Proof. We have a map (cf. [RS18, the first displayed formula in the proof of Proposition 2.10])

$$\begin{eqnarray}K_{r}^{M}(R)/U^{\text{}\underline{1}}K_{r}^{M}(R)\rightarrow \underset{1\leqslant i\leqslant d}{\bigoplus }\;K_{r}^{M}(R_{i});~\{a_{1},\ldots ,a_{r}\}\mapsto \oplus _{i}\{a_{1}~\text{mod}~T_{i},\ldots ,a_{r}~\text{mod}~T_{i}\},\end{eqnarray}$$

where $(a~\text{mod}~T_{i})\in R_{i}$ is the image of $a\in R$ . By [RS18, Proposition 2.10] and Proposition 1.1.3, we see that this map is injective. Combining with the fact that $\bigoplus _{1\leqslant i\leqslant d}K_{r}^{M}(R_{i})$ is $p$ -torsion free, we conclude this claim.◻

Claim 1.1.11. For $\text{}\underline{n}$ and $i$ as in Proposition 1.1.9, the multiplication by $p$ induces an injective map:

$$\begin{eqnarray}gr^{[\text{}\underline{n}/p],i}k_{r}^{M}(R)_{m-1}\rightarrow gr^{\text{}\underline{n},i}k_{r}^{M}(R)_{m}.\end{eqnarray}$$

Proof. It is easy to check that the multiplication by $p$ induces such a map. Its injectivity follows from the commutative diagram

and the commutative diagram

where the vertical isomorphisms are from Proposition 1.1.9. ◻

1.2 Relation with differential forms

The sheaf $\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ relates to coherent sheaves as follows.

Theorem 1.2.1. We have an exact sequence

$$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6FA}_{X|D,\log }^{r}\rightarrow \unicode[STIX]{x1D6FA}_{X|D}^{r}\xrightarrow[{}]{1-C^{-1}}\unicode[STIX]{x1D6FA}_{X|D}^{r}/d\unicode[STIX]{x1D6FA}_{X|D}^{r-1}\rightarrow 0,\end{eqnarray}$$

where $\unicode[STIX]{x1D6FA}_{X|D}^{r}=\unicode[STIX]{x1D6FA}_{X/k}^{r}(\log D)\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{X}(-D)$ .

Proof. For the exactness on the right, it suffices to show the surjectivity of $1-C^{-1}$ on sections over the strict henselization of a local ring of $X$ . In fact, by the argument in the classical case where $D=\emptyset$ [Mil76, Lemma 1.3], it suffices to show the following claim.

Claim 1.2.2. Let $A$ be a strictly henselian regular local ring of equi-characteristic $p>0$ and $\mathfrak{m}\subset A$ be the maximal ideal. Let $\unicode[STIX]{x1D70B}\in \mathfrak{m}$ and $a\in A$ . If $a\in \unicode[STIX]{x1D70B}A$ , then there exists $b\in A$ , such that $b\in \unicode[STIX]{x1D70B}A$ and $b^{p}-b=a$ .

Proof of Claim 1.2.2.

Let $k$ be the residue field of $A$ . Since $\unicode[STIX]{x1D719}:A\rightarrow A$ is surjective, there exists $\tilde{b}\in A$ such that $\tilde{b}^{p}-\tilde{b}=a$ . Letting $\unicode[STIX]{x1D6FD}\in k$ be the image of $\tilde{b}$ , $\unicode[STIX]{x1D6FD}^{p}-\unicode[STIX]{x1D6FD}=0\in k$ by the assumption $a\in \unicode[STIX]{x1D70B}A\subset \mathfrak{m}$ . Hence $\unicode[STIX]{x1D6FD}\in \mathbb{F}_{p}\subset A$ and we put $b=\tilde{b}-\unicode[STIX]{x1D6FD}\in A$ . Then

$$\begin{eqnarray}b(b^{p-1}-1)=b^{p}-b=\tilde{b}^{p}-\tilde{b}=a\in \unicode[STIX]{x1D70B}A.\end{eqnarray}$$

Since $b\in \mathfrak{m}_{A}$ by the construction, $b^{p-1}-1\in A^{\times }$ and we get $b\in \unicode[STIX]{x1D70B}A$ .◻

It remains to show the exactness in the middle, i.e., to show that $\unicode[STIX]{x1D6FA}_{X|D}^{r}\cap \unicode[STIX]{x1D6FA}_{X,\log }^{r}=\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ . This is a étale local question, which is a consequence of Proposition 1.2.3 below, which is a refinement of [Kat82, Proposition 1].◻

Let $R$ be the henselization of a local ring of $X$ and choose a system $T_{1},\ldots ,T_{d}$ of regular parameters of $R$ such that $\text{Supp}(D)=\text{Spec}(R/(T_{1}\cdots T_{e}))\subset \text{Spec}(R)$ for some $e\leqslant d=\text{dim}(R)$ . Let $\unicode[STIX]{x1D6FA}_{R}^{1}(\log D)$ denotes the module of differentials with logarithmic poles along $D$ and put $\unicode[STIX]{x1D6FA}_{R}^{q}(\log D)=\overset{q}{\wedge }\;\unicode[STIX]{x1D6FA}_{R}^{1}(\log D)$ . For a tuple of integers $\text{}\underline{n}=(n_{1},\ldots ,n_{e})$ with $n_{i}\geqslant 1$ , put

$$\begin{eqnarray}\displaystyle & \displaystyle G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}=(T_{1}^{n_{1}}\cdots T_{e}^{n_{e}})\cdot \unicode[STIX]{x1D6FA}_{R}^{q}(\log D)\;\subset \;\unicode[STIX]{x1D6FA}_{R}^{q}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle G^{\text{}\underline{n}}\unicode[STIX]{x1D708}_{R}(q)=\text{Ker}\big(G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}\xrightarrow[{}]{1-C^{-1}}\unicode[STIX]{x1D6FA}_{R}^{q}(\log D)/d\unicode[STIX]{x1D6FA}_{R}^{q-1}(\log D)\big). & \displaystyle \nonumber\end{eqnarray}$$

Proposition 1.2.3. $G^{\text{}\underline{n}}\unicode[STIX]{x1D708}_{R}(q)$ is generated by elements of the form

$$\begin{eqnarray}\displaystyle \frac{dx_{1}}{x_{1}}\wedge \cdots \wedge \displaystyle \frac{dx_{q}}{x_{q}}\quad \text{with}\;x_{1}\in 1+(T_{1}^{n_{1}}\cdots T_{e}^{n_{e}}),\quad x_{i}\in R\biggl[\frac{1}{T_{1}\cdots T_{e}}\biggr]^{\times }\quad (2\leqslant i\leqslant q).\end{eqnarray}$$

Proof. The following argument is a variant of Part (B) of the proof of [Kat82, Proposition 1 (see p. 224)]. By [Art69], we may replace $R$ by $R=k[[T_{1},\ldots ,T_{d}]]$ . Indeed, to use Artin approximation we have to equip any $R$ -algebra with the log structure coming via pullback from the canonical one on $(R,D)$ to extend the group $G^{\text{}\underline{n}}\unicode[STIX]{x1D708}_{R}(q)$ to a functor on $R$ -algebras $S\mapsto G^{\text{}\underline{n}}\unicode[STIX]{x1D708}_{S}(q)$ . Put $A=k[[T_{1},\ldots ,T_{d-1}]]$ and $T=T_{d}$ so that $R=A[[T]]$ . Let $\unicode[STIX]{x1D6FA}_{A}^{q}(\log E)$ be the module of differential $q$ -forms on $\text{Spec}(A)$ with logarithmic poles along $E=\text{Spec}(A/(T_{1}\cdots T_{d-1}))\subset \text{Spec}\,A$ . By [Kat82, Proposition 1], we have an isomorphism

(1.2.1) $$\begin{eqnarray}(R\otimes _{A}\unicode[STIX]{x1D6FA}_{A}^{q}(\log E))\oplus (R\otimes _{A}\unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E))\simeq \unicode[STIX]{x1D6FA}_{R}^{q}(\log D);\quad (a\otimes w,b\otimes v)\rightarrow aw+bv\wedge \displaystyle \frac{dT}{T}.\end{eqnarray}$$

For each $n\geqslant 1$ , let $V_{n}\subset \unicode[STIX]{x1D6FA}_{R}^{q}(\log D)$ be the image of

$$\begin{eqnarray}(T^{n}A[[T]]\otimes \unicode[STIX]{x1D6FA}_{A}^{q}(\log E))\oplus (T^{n}A[[T]]\otimes _{A}\unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)).\end{eqnarray}$$

We easily check the following.

Claim 1.2.4. For a tuple of integers $\text{}\underline{n}=(n_{1},\ldots ,n_{d-1},n)$ with $n,n_{i}\geqslant 1$ , we have $G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}\subset V_{n}$ and it coincides with the image of

$$\begin{eqnarray}(T^{n}A[[T]]\otimes _{A}(T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\cdot \unicode[STIX]{x1D6FA}_{A}^{q}(\log E))\oplus (T^{n}A[[T]]\otimes _{A}(T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\cdot \unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)).\end{eqnarray}$$

The map (1.2.1) restricted on $V_{n}$ induces an isomorphism

$$\begin{eqnarray}\displaystyle & \displaystyle (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\cdot \unicode[STIX]{x1D6FA}_{A}^{q}(\log E)\oplus (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\cdot \unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)\xrightarrow[{}]{\cong }G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}/G^{\text{}\underline{n}^{\prime }}\unicode[STIX]{x1D6FA}_{R}^{q}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle (w,v)\rightarrow T^{n}\biggl(w+v\wedge \displaystyle \frac{dT}{T}\biggr), & \displaystyle \nonumber\end{eqnarray}$$

where $\text{}\underline{n}^{\prime }=(n_{1},\ldots ,n_{d-1},n+1)$ .

Let $I_{q}$ be the set of strictly increasing functions $\{1,\ldots ,q\}\rightarrow \{1,\ldots ,d-1\}$ . For $s\in I_{q}$ write

$$\begin{eqnarray}\unicode[STIX]{x1D714}_{s}=\displaystyle \frac{dT_{s(1)}}{T_{s(1)}}\wedge \cdots \wedge \displaystyle \frac{dT_{s(q)}}{T_{s(q)}}\in \unicode[STIX]{x1D6FA}_{A}^{q}(\log E).\end{eqnarray}$$

Then $\unicode[STIX]{x1D714}_{s}$ ( $s\in I_{q}$ ) form a basis of $\unicode[STIX]{x1D6FA}_{A}^{q}(\log E)$ over $A$ . Put

$$\begin{eqnarray}U_{n}=V_{n}\cap \text{Ker}\big(\unicode[STIX]{x1D6FA}_{R}^{q}(\log D)\xrightarrow[{}]{1-C^{-1}}\unicode[STIX]{x1D6FA}_{R}^{q}(\log D)/d\unicode[STIX]{x1D6FA}_{R}^{q-1}(\log D)\big).\end{eqnarray}$$

We have the following description of $U_{n}/U_{n+1}$ (see Part (B) of the proof of [Kat82, Proposition 1]).

If $(p,n)=1$ , we have an isomorphism

(1.2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{n}:\unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)\xrightarrow[{}]{\cong }U_{n}/U_{n+1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathop{\sum }_{s\in I_{q-1}}a_{s}\unicode[STIX]{x1D714}_{s}\mapsto \mathop{\sum }_{s\in I_{q-1}}\displaystyle \frac{d(1+a_{s}T^{n})}{(1+a_{s}T^{n})}\wedge \unicode[STIX]{x1D714}_{s}\quad (a_{s}\in A). & \displaystyle\end{eqnarray}$$

If $p|n$ , we have an isomorphism

(1.2.3) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70C}_{n}:\unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)/\unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)_{d=0}\oplus \unicode[STIX]{x1D6FA}_{A}^{q-2}(\log E)/\unicode[STIX]{x1D6FA}_{A}^{q-2}(\log E)_{d=0}\xrightarrow[{}]{\cong }U_{n}/U_{n+1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \biggl(\mathop{\sum }_{s\in I_{q-1}}a_{s}\unicode[STIX]{x1D714}_{s},\mathop{\sum }_{t\in I_{q-2}}b_{t}\unicode[STIX]{x1D714}_{t}\biggr)\mapsto \mathop{\sum }_{s\in I_{q-1}}\displaystyle \frac{d(1+a_{s}T^{n})}{(1+a_{s}T^{n})}\wedge \unicode[STIX]{x1D714}_{s}+\mathop{\sum }_{t\in I_{q-2}}\displaystyle \frac{d(1+b_{t}T^{n})}{(1+b_{t}T^{n})}\wedge \displaystyle \frac{dT}{T}\wedge \unicode[STIX]{x1D714}_{t}, & \displaystyle\end{eqnarray}$$

where $a_{s},b_{t}\in A$ .

Claim 1.2.5. Fix a tuple of integers $\text{}\underline{n}=(n_{1},\ldots ,n_{d-1},n)$ with $n_{i}\geqslant 1$ .

1. (1) Assume $(p,n)=1$ and $\unicode[STIX]{x1D70C}_{n}(\unicode[STIX]{x1D714})\in G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}\hspace{0.6em}{\rm mod}\hspace{0.2em}U_{n+1}$ for

   $$\begin{eqnarray}\unicode[STIX]{x1D714}=\underset{s\in I_{q-1}}{\sum }a_{s}\unicode[STIX]{x1D714}_{s}\in \unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E).\end{eqnarray}$$
   Then we have $a_{s}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})$ for all $s\in I_{q-1}$ .

2. (2) Assume $p|n$ and $\unicode[STIX]{x1D70C}_{n}(\unicode[STIX]{x1D714})\in G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}\hspace{0.6em}{\rm mod}\hspace{0.2em}U_{n+1}$ for

   $$\begin{eqnarray}\unicode[STIX]{x1D714}=(\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2})\in \unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)/\unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)_{d=0}\oplus \unicode[STIX]{x1D6FA}_{A}^{q-2}(\log E)/\unicode[STIX]{x1D6FA}_{A}^{q-2}(\log E)_{d=0}.\end{eqnarray}$$
   Then one can write
   $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D714}_{1}=\underset{s\in I_{q-1}}{\sum }a_{s}\unicode[STIX]{x1D714}_{s}\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)_{d=0}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D714}_{2}=\underset{t\in I_{q-2}}{\sum }b_{t}\unicode[STIX]{x1D714}_{t}\hspace{0.6em}{\rm mod}\hspace{0.2em}\unicode[STIX]{x1D6FA}_{A}^{q-2}(\log E)_{d=0}, & \displaystyle \nonumber\end{eqnarray}$$
   with $a_{s},b_{t}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})$ for all $s\in I_{q-1}$ and $t\in I_{q-2}$ .

Proof of Claim 1.2.5.

Assume $(p,n)=1$ . From (1.2.2) we get

$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{n}\biggl(\underset{s\in I_{q-1}}{\sum }a_{s}\unicode[STIX]{x1D714}_{s}\biggr)=T^{n}\underset{s\in I_{q-1}}{\sum }da_{s}\wedge \unicode[STIX]{x1D714}_{s}\pm nT^{n}\underset{s\in I_{q-1}}{\sum }a_{s}\unicode[STIX]{x1D714}_{s}\wedge \displaystyle \frac{dT}{T}\;\hspace{0.6em}{\rm mod}\hspace{0.2em}U_{n+1}.\end{eqnarray}$$

Hence (1) follows from Claim 1.2.4 noting $da_{s}\wedge \unicode[STIX]{x1D714}_{s}\in \unicode[STIX]{x1D6FA}_{A}^{q}(\log E)$ . Next assume $p|n$ . From (1.2.3) we get

$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{n}\biggl(\biggl(\underset{s\in I_{q-1}}{\sum }a_{s}\unicode[STIX]{x1D714}_{s},\underset{t\in I_{q-2}}{\sum }b_{t}\unicode[STIX]{x1D714}_{t}\biggr)\biggr)=T^{n}\underset{s\in I_{q-1}}{\sum }da_{s}\wedge \unicode[STIX]{x1D714}_{s}\pm T^{n}\underset{t\in I_{q-2}}{\sum }db_{t}\wedge \unicode[STIX]{x1D714}_{t}\wedge \displaystyle \frac{dT}{T}.\end{eqnarray}$$

By Claim 1.2.4, if the left-hand side lies in $G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}\hspace{0.6em}{\rm mod}\hspace{0.2em}U_{n+1}$ , we get

$$\begin{eqnarray}da_{s}\wedge \unicode[STIX]{x1D714}_{s}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\cdot \unicode[STIX]{x1D6FA}_{A}^{q}(\log E),\quad db_{t}\wedge \unicode[STIX]{x1D714}_{t}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\cdot \unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E).\end{eqnarray}$$

Thus the desired assertion follows from the following.

Claim 1.2.6. Assume $d\unicode[STIX]{x1D702}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\cdot \unicode[STIX]{x1D6FA}_{A}^{q}(\log E)$ for $\unicode[STIX]{x1D702}=\sum _{s\in I_{q-1}}a_{s}\unicode[STIX]{x1D714}_{s}\in \unicode[STIX]{x1D6FA}_{A}^{q-1}(\log E)$ . Then there exist $\unicode[STIX]{x1D6FC}_{s}\in A$ for $s\in I_{q-1}$ such that $a_{s}-\unicode[STIX]{x1D6FC}_{s}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})$ for all $s$ and that $d\unicode[STIX]{x1D709}=0$ for $\unicode[STIX]{x1D709}=\sum _{s\in I_{q-1}}\unicode[STIX]{x1D6FC}_{s}\unicode[STIX]{x1D714}_{s}$ .

Indeed write $a_{s}=\unicode[STIX]{x1D6FC}_{s}+a_{s}^{\prime }$ where $a_{s}^{\prime }\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})$ and $\unicode[STIX]{x1D6FC}_{s}$ are expanded as

$$\begin{eqnarray}\underset{i_{1},\ldots ,i_{d-1}}{\sum }\unicode[STIX]{x1D6FC}_{s,i_{1},\ldots ,i_{d-1}}T_{1}^{i_{1}}\cdots T_{d-1}^{i_{d-1}}\quad (\unicode[STIX]{x1D6FC}_{s,i_{1},\ldots ,i_{d-1}}\in k),\end{eqnarray}$$

where $i_{1},\ldots ,i_{d-1}$ range over non-negative integers such that there exists $1\leqslant \unicode[STIX]{x1D708}\leqslant d-1$ with $i_{\unicode[STIX]{x1D708}}<n_{\unicode[STIX]{x1D708}}$ . Then one easily check that $\unicode[STIX]{x1D6FC}_{s}$ satisfy the desired condition.◻

Now we can finish the proof of Proposition 1.2.3. In the following we fix a tuple of integers $\text{}\underline{n}=(n_{1},\ldots ,n_{d-1},n_{d})$ with $n_{i}\geqslant 1$ and take $\unicode[STIX]{x1D714}\in G^{\text{}\underline{n}}\unicode[STIX]{x1D6FA}_{R}^{q}$ . By Claim 1.2.5 there exist a series of elements

$$\begin{eqnarray}\displaystyle & a_{s,n}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\quad (s\in I_{q-1},n\geqslant n_{d}), & \displaystyle \nonumber\\ \displaystyle & b_{t,pm}\in (T_{1}^{n_{1}}\cdots T_{d-1}^{n_{d-1}})\quad (t\in I_{q-2},m\geqslant n_{d}/p), & \displaystyle \nonumber\end{eqnarray}$$

such that

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714} & = & \displaystyle \underset{n\geqslant n_{d}}{\sum }\;\underset{s\in I_{q-1}}{\sum }\displaystyle \frac{d(1+a_{s,n}T^{n})}{(1+a_{s,n}T^{n})}\wedge \unicode[STIX]{x1D714}_{s}+\underset{pm\geqslant n_{d}}{\sum }\;\underset{t\in I_{q-2}}{\sum }\displaystyle \frac{d(1+b_{t,m}T^{pm})}{(1+b_{t,m}T^{pm})}\wedge \displaystyle \frac{dT}{T}\wedge \unicode[STIX]{x1D714}_{t}\nonumber\\ \displaystyle & = & \displaystyle \underset{s\in I_{q-1}}{\sum }\bigg(\underset{n\geqslant n_{d}}{\sum }\displaystyle \frac{d(1+a_{s,n}T^{n})}{(1+a_{s,n}T^{n})}\bigg)\wedge \unicode[STIX]{x1D714}_{s}+\underset{t\in I_{q-2}}{\sum }\bigg(\underset{pm\geqslant n_{d}}{\sum }\displaystyle \frac{d(1+b_{t,m}T^{pm})}{(1+b_{t,m}T^{pm})}\bigg)\wedge \displaystyle \frac{dT}{T}\wedge \unicode[STIX]{x1D714}_{t}.\nonumber\end{eqnarray}$$

The products

$$\begin{eqnarray}x=\underset{n\geqslant n_{d}}{\prod }(1+a_{s,n}T^{n}),\quad y=\underset{pm\geqslant n_{d}}{\prod }(1+b_{t,m}T^{pm})\end{eqnarray}$$

converge in $1+(T_{1}^{n_{1}}\cdots T_{d}^{n_{d}})\subset R^{\times }$ and we get

$$\begin{eqnarray}\unicode[STIX]{x1D714}=\underset{s\in I_{q-1}}{\sum }\displaystyle \frac{dx}{x}\wedge \unicode[STIX]{x1D714}_{s}+\underset{t\in I_{q-2}}{\sum }\displaystyle \frac{dy}{y}\wedge \displaystyle \frac{dT}{T}\wedge \unicode[STIX]{x1D714}_{t}.\end{eqnarray}$$

This completes the proof of Proposition 1.2.3. ◻

Remark 1.2.7. In fact, the above proof shows that the exactness in the middle of the complex in Theorem 1.2.1 already holds in the Nisnevich topology.

2 Filtered de Rham–Witt complexes

Let $X,D,j::U{\hookrightarrow}X$ be as before. Let $\{D_{\unicode[STIX]{x1D706}}\}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$ be the (smooth) irreducible components of $D$ . We endow $\mathbb{Z}^{\unicode[STIX]{x1D6EC}}$ with a semi-order by

(2.0.1) $$\begin{eqnarray}\text{}\underline{n}:=(n_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\geqslant \text{}\underline{n^{\prime }}:=(n_{\unicode[STIX]{x1D706}}^{\prime })_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\;\text{if}\;n_{\unicode[STIX]{x1D706}}\geqslant n_{\unicode[STIX]{x1D706}}^{\prime }\quad \text{for all}\;\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}.\end{eqnarray}$$

For $\text{}\underline{n}=(n_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\in \mathbb{Z}^{\unicode[STIX]{x1D6EC}}$ let

$$\begin{eqnarray}D_{\text{}\underline{n}}=\mathop{\sum }_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}n_{\unicode[STIX]{x1D706}}D_{\unicode[STIX]{x1D706}}\end{eqnarray}$$

be the associated divisor.

2.1 Definition and basic properties

Let $E$ be a Cartier divisor on $X$ . It is given by $\{V_{i},f_{i}\}$ , where $\{V_{i}\}_{i}$ is an open cover of $X$ and $f_{i}\in \unicode[STIX]{x1D6E4}(V_{i},{\mathcal{M}}_{X}^{\times })$ is a section of the sheaf of total fractional ring.

Definition 2.1.1. We define an invertible $W_{m}{\mathcal{O}}_{X}$ -module $W_{m}{\mathcal{O}}_{X}(E)$ associated to $E$ as

$$\begin{eqnarray}W_{m}{\mathcal{O}}_{X}(E)_{|V_{i}}:=W_{m}{\mathcal{O}}_{V_{i}}\cdot \biggl[\frac{1}{f_{i}}\biggr]_{m}\subset W_{m}{\mathcal{M}}_{V_{i}},\end{eqnarray}$$

where $[\cdot ]_{m}:{\mathcal{O}}\rightarrow W_{m}{\mathcal{O}}$ the Teichmüller lifting.

This definition gives us an invertible sheaf $W_{m}{\mathcal{O}}_{X}(D_{\text{}\underline{n}})$ for any $D_{\text{}\underline{n}}$ as above.

Lemma 2.1.2. We have:

1. (i) $F(W_{m+1}{\mathcal{O}}_{X}(D_{\text{}\underline{n}}))\subset W_{m}{\mathcal{O}}_{X}(D_{p\text{}\underline{n}})$ ;

2. (ii) $V(W_{m}{\mathcal{O}}_{X}(D_{p\text{}\underline{n}}))\subset W_{m+1}{\mathcal{O}}_{X}(D_{\text{}\underline{n}})$ ;

3. (iii) $R(W_{m+1}{\mathcal{O}}_{X}(D_{\text{}\underline{n}}))\subset W_{m}{\mathcal{O}}_{X}(D_{\text{}\underline{n}})$ .

Proof. The claims (i) and (iii) are clear by the definition. Claim (ii) follows from the equalities $V(x\cdot Fy)=V(x)\cdot y$ and $F[y]_{m+1}=[y^{p}]_{m}$ .◻

Let $W_{m}\unicode[STIX]{x1D6FA}_{X}^{\ast }(\log D)$ be the de Rham–Witt complex with respect to the canonical log structure $(X,j_{\ast }{\mathcal{O}}_{U}^{\times }\cap {\mathcal{O}}_{X})$ defined in [HK94, § 4].

Definition 2.1.3. For $\text{}\underline{n}=(n_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\in \mathbb{Z}^{\unicode[STIX]{x1D6EC}}$ , we define the filtered de Rham–Witt complex as

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast }:=W_{m}{\mathcal{O}}_{X}(-D_{\text{}\underline{n}})\cdot W_{m}\unicode[STIX]{x1D6FA}_{X}^{\ast }(\log D)\subset j_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U}^{\ast },\end{eqnarray}$$

where $W_{m}\unicode[STIX]{x1D6FA}_{X}^{\ast }(\log D)$ is canonically viewed as a subsheaf of $j_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U}^{\ast }$ (cf. [HK94, (4.20)]).

Note that

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast }\cong W_{m}\unicode[STIX]{x1D6FA}_{X}^{\ast }(\log D)\otimes _{W_{m}{\mathcal{O}}_{X}}W_{m}{\mathcal{O}}_{X}(-D_{\text{}\underline{n}}).\end{eqnarray}$$

In particular, $W_{1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast }=\unicode[STIX]{x1D6FA}_{X}^{\ast }(\log D)\otimes {\mathcal{O}}_{X}(-D_{\text{}\underline{n}})=\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast }$ (cf. notation in Theorem 1.2.1).

Lemma 2.1.4. We have the following inclusions:

1. (i) $F(W_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast })\subset W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{\ast }$ ;

2. (ii) $V(W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{\ast })\subset W_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast }$ ;

3. (iii) $R(W_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast })\subset W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{\ast }$ .

Proof. This follows from Lemma 2.1.2 and the basic properties of de Rham–Witt complex [HK94, § 4.1] [Lor02, Proposition 1.5]. ◻

2.2 Canonical filtration

On $W_{m}\unicode[STIX]{x1D6FA}_{X}^{\ast }(\log D)$ , we can define the canonical filtration as in [Ill79, I (3.1.1)]:

$$\begin{eqnarray}\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D):=\left\{\begin{array}{@{}ll@{}}W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)\quad & \text{if}\;s\leqslant 0\;\text{or}\;r\leqslant 0,\\ \text{Ker}(R^{m-s}:W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)\rightarrow W_{s}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D))\quad & \text{if}~1\leqslant s\leqslant m,\\ 0\quad & \text{if}~s\geqslant m.\end{array}\right.\end{eqnarray}$$

For $1\leqslant s\leqslant m$ , we have [Lor02, Proposition 1.16]

$$\begin{eqnarray}\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)=V^{s}W_{m-s}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)+dV^{s}W_{m-s}\unicode[STIX]{x1D6FA}_{X}^{r-1}(\log D).\end{eqnarray}$$

Definition 2.2.1. For $1\leqslant s\leqslant m$ , we define

$$\begin{eqnarray}\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}:=\left\{\begin{array}{@{}ll@{}}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\quad & \text{if}\;s\leqslant 0\;\text{or}\;r\leqslant 0,\\ \text{Ker}(R^{m-s}:W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\rightarrow W_{s}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r})\quad & \text{if}~1\leqslant s\leqslant m,\\ 0\quad & \text{if}~s\geqslant m.\end{array}\right.\end{eqnarray}$$

Theorem 2.2.2. We have

$$\begin{eqnarray}\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}=V^{s}W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r}+dV^{s}W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r-1}.\end{eqnarray}$$

Proof. We only need to show the inclusion ‘ $\subseteq$ ’. By the definition of the canonical filtration and the fact that $W_{m}{\mathcal{O}}_{X}(-D_{\text{}\underline{n}})$ is an invertible sheaf, we have

$$\begin{eqnarray}\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}=W_{m}{\mathcal{O}}_{X}(-D_{\text{}\underline{n}})\cdot \text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D),\end{eqnarray}$$

and it suffices to show that the group on the right-hand side is contained in

$$\begin{eqnarray}V^{s}W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r}+dV^{s}W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r-1}.\end{eqnarray}$$

Using the formula $x\cdot Vy=V(F(x)\cdot y)$ repeatedly, we see that for any $\unicode[STIX]{x1D714}\in W_{m-s}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)$ , $\unicode[STIX]{x1D714}^{\prime }\in W_{m-s}\unicode[STIX]{x1D6FA}_{X}^{r-1}(\log D)$ and $x\in W_{m}{\mathcal{O}}_{X}(-D_{\text{}\underline{n}})$ ,

(2.2.1) $$\begin{eqnarray}x\cdot (V^{s}(\unicode[STIX]{x1D714})+dV^{s}(\unicode[STIX]{x1D714}^{\prime }))=V^{s}(F^{s}(x)\cdot \unicode[STIX]{x1D714})+dV^{s}(F^{s}(x)\cdot \unicode[STIX]{x1D714}^{\prime })\pm dx\cdot V^{s}(\unicode[STIX]{x1D714}^{\prime }).\end{eqnarray}$$

By our definition, we have $F^{s}(x)\cdot \unicode[STIX]{x1D714}\in W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r}$ and $F^{s}(x)\cdot \unicode[STIX]{x1D714}^{\prime }\in W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r-1}$ . It suffices to prove that $dx\cdot V^{s}(\unicode[STIX]{x1D714}^{\prime })\in V^{s}W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r}$ . Since the problem is local on $X$ , it is enough to show the following claim.

Claim 2.2.3. For any $t\in {\mathcal{O}}_{X}$ , and $z^{\prime }\in W_{m-s}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)$ ,

$$\begin{eqnarray}d[t]_{m}V^{s}(z^{\prime })=V^{s}([t]_{m-s}^{p^{s}-1}d[t]_{m-s}z^{\prime }).\end{eqnarray}$$

Indeed, we know (cf. [Ill79, I, Proposition 1.5.2]),

$$\begin{eqnarray}d[t]_{m}V(z)=V([t]_{m-1}^{p-1}d[t]_{m-1}z)\quad \text{for any}~t\in {\mathcal{O}}_{X},\text{ and }z\in W_{m-1}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D).\end{eqnarray}$$

Using this formula and $x\cdot Vy=V(F(x)\cdot y)$ repeatedly, we get the claim.◻

Corollary 2.2.4. There are the following inclusions:

1. (i) $F(\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r})\subset \text{Fil}^{s-1}W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}$ ;

2. (ii) $V(\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r})\subset \text{Fil}^{s+1}W_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ ;

3. (iii) $R(\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r})\subset \text{Fil}^{s}W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ .

Proof. This follows from Lemma 2.1.4, $FV=p=VF$ and $FdV=d$ .◻

For $\text{}\underline{n}\geqslant \text{}\underline{1}$ , i.e. $\text{}\underline{n}\in \mathbb{N}^{\unicode[STIX]{x1D6EC}}$ , we have

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\subset W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}.\end{eqnarray}$$

Indeed, for $m=1$ this follows from the fact $W_{1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}=\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)(-D_{\text{}\underline{n}})\subset \unicode[STIX]{x1D6FA}_{X}^{r}$ . Then the claim follows by induction on $m$ using Theorem 2.2.2.

Lemma 2.2.5. For $\text{}\underline{n}\in \mathbb{N}^{\unicode[STIX]{x1D6EC}}$ , we have

$$\begin{eqnarray}\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}\cap W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}=\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r},\end{eqnarray}$$

and

$$\begin{eqnarray}\text{Ker}(p^{s}:W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\rightarrow W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r})=\text{Fil}^{m-s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}.\end{eqnarray}$$

In particular the multiplication by $p^{s}$ induces an injective homomorphism

(2.2.2) $$\begin{eqnarray}\text{}\underline{p^{s}}:W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}{\hookrightarrow}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}.\end{eqnarray}$$

Proof. The first equality follows from the following commutative diagram.

The second equality follows from the first and the fact (cf. [Ill79, I, Proposition 3.11])

$$\begin{eqnarray}\text{Ker}(p^{s}:W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow W_{m}\unicode[STIX]{x1D6FA}_{X}^{r})=\text{Fil}^{m-s}W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}.\square\end{eqnarray}$$

Recall (cf. the proof of [Ill79, I, Proposition 3.11, p. 575])

(2.2.3) $$\begin{eqnarray}\displaystyle & \displaystyle \text{Ker}(F^{m-1}:W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{X}^{r})=VW_{m-1}\unicode[STIX]{x1D6FA}_{X}^{r}, & \displaystyle\end{eqnarray}$$

(2.2.4) $$\begin{eqnarray}\displaystyle & \displaystyle \text{Ker}(F^{m-1}d:W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{X}^{r+1})=FW_{m+1}\unicode[STIX]{x1D6FA}_{X}^{r}. & \displaystyle\end{eqnarray}$$

We have the following analogues for the filtered de Rham–Witt sheaves.

Proposition 2.2.6. For $\text{}\underline{n}\in \mathbb{N}^{\unicode[STIX]{x1D6EC}}$ , we have:

1. (i) $\text{Ker}(F^{m-1}:W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}}}^{r})=VW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}$ , i.e.,

   $$\begin{eqnarray}VW_{m-1}\unicode[STIX]{x1D6FA}_{X}^{r}\cap W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}=VW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r};\end{eqnarray}$$

2. (ii) $\text{Ker}(F^{m-1}d:W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{X|D_{p^{m}\text{}\underline{n}}}^{r+1})=FW_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ , i.e.,

   $$\begin{eqnarray}FW_{m+1}\unicode[STIX]{x1D6FA}_{X}^{r}\cap W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}=FW_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}.\end{eqnarray}$$

Proof. This is proved by the same argument as in the proof of [Ill79, I, Proposition 3.11], which we recall below.

(i) For $m=1$ it is trivial. For $m>1$ we have

$$\begin{eqnarray}\text{Ker}\,F^{m-1}\subset \text{Ker}\,p^{m-1}=\text{Fil}^{1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}=VW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}+dVW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r-1}.\end{eqnarray}$$

by Theorem 2.2.2 and Lemma 2.2.5. It suffices to show that, for $1\leqslant s\leqslant m$ ,

(2.2.5) $$\begin{eqnarray}(\text{Ker}\,F^{m-1})\cap (VW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}+\text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r})\subset VW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}+\text{Fil}^{s+1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}.\end{eqnarray}$$

Let $z=Vx+dV^{s}y$ with $x\in W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}$ , $y\in W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r-1}$ be such that $F^{m-1}z=0$ . Noting $F^{m-1}Vx=pF^{m-2}x=0$ and $F^{m-1}dV^{s}=F^{m-1-s}d$ , it follows that $F^{m-1-s}dy=0$ . Let $\overline{y}$ be the image of $y$ in $\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r-1}$ under the restriction map $R^{m-1-s}$ . Then, by [Ill79, I, Proposition 3.3], we get $C^{-(m-1-s)}d\overline{y}=0$ and $d\overline{y}=0$ in $\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r}$ . By Lemma 1.1.8 there exists (locally) $y^{\prime }\in \unicode[STIX]{x1D6FA}_{X|D_{p^{s-1}\text{}\underline{n}}}^{r-1}$ such that $\overline{y}=C^{-1}(y^{\prime })$ . We can then take a lift ${\tilde{y}}$ of $y^{\prime }$ in $W_{m+1-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s-1}\text{}\underline{n}}}^{r-1}$ . Indeed, writing $y^{\prime }=\sum _{\unicode[STIX]{x1D6FC}}a_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}$ with $a_{\unicode[STIX]{x1D6FC}}\in {\mathcal{O}}_{X}(-D_{p^{s-1}\text{}\underline{n}})$ and $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}\in \unicode[STIX]{x1D6FA}_{X}^{r-1}(\log D)$ , we take ${\tilde{y}}=\sum _{\unicode[STIX]{x1D6FC}}[a_{\unicode[STIX]{x1D6FC}}]_{m+1-s}\tilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D6FC}}$ , where $\tilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D6FC}}\in W_{m+1-s}\unicode[STIX]{x1D6FA}_{X}^{r-1}(\log D)$ is a lift of $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6FC}}$ . By the construction we have

$$\begin{eqnarray}y=F{\tilde{y}}\;\text{mod}\;\text{Fil}^{1}W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}\text{}\underline{n}}}^{r-1}.\end{eqnarray}$$

By taking $V^{s}$ on both sides, we get

$$\begin{eqnarray}V^{s}y=V^{s}F{\tilde{y}}\;\text{mod}\;\text{Fil}^{s+1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r-1}.\end{eqnarray}$$

Hence

$$\begin{eqnarray}dV^{s}y=dV^{s}F{\tilde{y}}=pdV^{s-1}{\tilde{y}}=VdV^{s-2}{\tilde{y}}\;\text{mod}\;\text{Fil}^{s+1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r-1}.\end{eqnarray}$$

That is

$$\begin{eqnarray}dV^{s}y\in VW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}+\text{Fil}^{s+1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}.\end{eqnarray}$$

Hence $z=Vx+dV^{s}y\in VW_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}+\text{Fil}^{s+1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ , which proves (2.2.5).

(ii) It suffices to prove that, for $1\leqslant s\leqslant m$ ,

(2.2.6) $$\begin{eqnarray}\text{Ker}(F^{m-1}d)\cap \text{Fil}^{s}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}\subset FW_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}+\text{Fil}^{s+1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}.\end{eqnarray}$$

Let $z=V^{s}x+dV^{s}y$ with $x\in W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s+1}\text{}\underline{n}}}^{r}$ , $y\in W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s+1}\text{}\underline{n}}}^{r-1}$ be such that $F^{m-1}dz=0$ . Noting $F^{m-1}dV^{s}=F^{m-1-s}d$ , it follows that $F^{m-1-s}dx=0$ . Let $\overline{x}$ be the image of $x$ in $\unicode[STIX]{x1D6FA}_{X|D_{p^{s+1}\text{}\underline{n}}}^{r}$ . As in (i), there exist $\tilde{x}\in W_{m-s+1}\unicode[STIX]{x1D6FA}_{X|D_{p^{s}n}}^{r}$ , such that

$$\begin{eqnarray}x=F\tilde{x}\;\text{mod}\;\text{Fil}^{1}W_{m-s}\unicode[STIX]{x1D6FA}_{X|D_{p^{s+1}\text{}\underline{n}}}^{r}.\end{eqnarray}$$

By taking $V^{s}$ on both sides, we obtain

$$\begin{eqnarray}V^{s}x=FV^{s}\tilde{x}\;\text{mod}\;\text{Fil}^{s+1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{pn}}^{r}.\end{eqnarray}$$

Noting that $dV^{s}y=FdV^{s+1}y\in FW_{m+1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ , we obtain the inclusion (2.2.6).◻

Corollary 2.2.7. For $\text{}\underline{n}\in \mathbb{N}^{\unicode[STIX]{x1D6EC}}$ and $x\in W_{m-1}\unicode[STIX]{x1D6FA}_{X}^{r}$ , $\text{}\underline{p}\cdot x\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ (cf. (2.2.2)) implies $x\in W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ .

Proof. Recall we have the following diagram [Ill79, Proposition 3.4].

Hence there exists $\tilde{x}\in W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}$ such that $p\tilde{x}=\text{}\underline{p}\cdot x$ and $R\tilde{x}=x$ . By the assumption, we have $VF\tilde{x}=p\tilde{x}=\text{}\underline{p}\cdot x\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ . Thanks to Corollary 2.2.6(i), it follows that there exists $y^{\prime }\in W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}$ such that

$$\begin{eqnarray}VF\tilde{x}=Vy^{\prime }.\end{eqnarray}$$

Recall the identity in [Ill79, I. 3.21.1.4]:

$$\begin{eqnarray}\text{Ker}(V:W_{m-1}\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow W_{m}\unicode[STIX]{x1D6FA}_{X}^{r})=FdV^{m-1}\unicode[STIX]{x1D6FA}_{X}^{r-1}.\end{eqnarray}$$

Therefore there exists $z^{\prime }\in \unicode[STIX]{x1D6FA}_{X}^{r-1}$ such that $F\tilde{x}-y^{\prime }=FdV^{m-1}z^{\prime }$ . That is

$$\begin{eqnarray}F(\tilde{x}-dV^{m-1}z^{\prime })=y^{\prime }\in W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}.\end{eqnarray}$$

Corollary 2.2.6(ii) implies that there exists $y^{\prime \prime }\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ such that

$$\begin{eqnarray}F(\tilde{x}-dV^{m-1}z^{\prime })=Fy^{\prime \prime }.\end{eqnarray}$$

Thanks to the identity [Ill79, I. 3.21.1.2]

$$\begin{eqnarray}\text{Ker}(F:W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow W_{m-1}\unicode[STIX]{x1D6FA}_{X}^{r})=V^{m-1}\unicode[STIX]{x1D6FA}_{X}^{r},\end{eqnarray}$$

we find $z^{\prime \prime }\in \unicode[STIX]{x1D6FA}_{X}^{r}$ such that

$$\begin{eqnarray}\tilde{x}-y^{\prime \prime }=dV^{m-1}z^{\prime }+V^{m-1}z^{\prime \prime }.\end{eqnarray}$$

Noting that $\text{Ker}(R:W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}\rightarrow W_{m-1}\unicode[STIX]{x1D6FA}_{X}^{r})=V^{m-1}\unicode[STIX]{x1D6FA}_{X}^{r}+dV^{m-1}\unicode[STIX]{x1D6FA}_{X}^{r-1}$ , we get

$$\begin{eqnarray}x=R\tilde{x}=Ry^{\prime \prime }\in W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}.\Box\end{eqnarray}$$

2.3 Logarithmic part of filtered de Rham–Witt complexes

The relation between the filtered de Rham–Witt sheaves and the relative logarithmic de Rham–Witt sheaves is given by the following theorem, which is a generalization of Theorem 1.2.1.

We first introduce some notations. Let

$$\begin{eqnarray}\unicode[STIX]{x1D6F4}:=\{D_{\text{}\underline{n}}\;|\;\text{}\underline{n}=(n_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\in \mathbb{N}^{\unicode[STIX]{x1D6EC}}\}\end{eqnarray}$$

be the set of effective divisors with supports in $X-U$ , whose irreducible components are same as those of $D$ . The semi-order on $\mathbb{Z}^{\unicode[STIX]{x1D6EC}}$ defined in (2.0.1) induces a semi-order on $\unicode[STIX]{x1D6F4}$ :

$$\begin{eqnarray}D_{\text{}\underline{n}}\geqslant D_{\text{}\underline{n^{\prime }}}\quad \text{if}\;\text{}\underline{n}\geqslant \text{}\underline{n^{\prime }}.\end{eqnarray}$$

For $D_{1},D_{2}\in \unicode[STIX]{x1D6F4}$ with $D_{1}\geqslant D_{2}$ , we have a natural injective map $W_{m}\unicode[STIX]{x1D6FA}_{X|D_{1},\log }^{r}{\hookrightarrow}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{2},\log }^{r}$ (see Corollary 1.1.4), which gives a pro-system of sheaves

In order to simplify the notation, we simply write it as “ $\mathop{\varprojlim }\nolimits_{D}$ ” $W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ .

Theorem 2.3.1. We have the following exact sequence of pro-sheaves,

where $D$ runs over the set $\unicode[STIX]{x1D6F4}$ .

We need the following lemma, which follows from easy calculations with Witt vectors.

Lemma 2.3.2 [GH06, Lemma 1.2.3].

Let $R$ be any ring, and $t\in R$ , then $[1+t]_{m}-[1]_{m}=(y_{0},\ldots ,y_{m-1})$ with $y_{i}\equiv t$ mod $t^{2}R$ for $0\leqslant i\leqslant m-1$ . Here $[x]_{m}=(x,0,\ldots ,0)\in W_{m}(R)$ is the Teichmüller representative of $x\in R$ .

Proof of Theorem 2.3.1.

First we show that $W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}},\log }^{r}\subset j_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r}$ (cf. Definition 1.1.1) lies in $W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ . This is a local question so that we may assume that $X=\text{Spec}(A)$ and $D=(t)$ for some $t\in A$ . By Lemma 2.3.2 we can write

$$\begin{eqnarray}[1+t^{p^{(m-1)}n}a]_{m}-[1]_{m}=(t^{p^{(m-1)}n}y_{0},\ldots ,t^{p^{(m-1)}n}y_{m-1})\end{eqnarray}$$

with $y_{i}\in A$ for $0\leqslant i\leqslant m-1$ . Noting $dx=0$ for $x\in W_{m}(\mathbb{F}_{p})$ , we get

$$\begin{eqnarray}d[1+t^{p^{(m-1)}n}a]_{m}=d(t^{p^{(m-1)}n}y_{0},\ldots ,t^{p^{(m-1)}n}y_{m-1})=d([t]_{m}^{n}\cdot (c_{0},\ldots ,c_{m-1}))\end{eqnarray}$$

with $c_{i}\in A$ for $0\leqslant i\leqslant m-1$ , where the second equality follows from the formula

$$\begin{eqnarray}[t]_{m}^{n}\cdot (c_{0},\ldots ,c_{m-1})=(t^{n}c_{0},t^{np}c_{1},\ldots ,t^{np^{(m-1)}}c_{m-1}).\end{eqnarray}$$

Hence we get

(2.3.1) $$\begin{eqnarray}d\log [1+t^{p^{m-1}n}]_{m}=([1+t^{p^{m-1}n}]_{m})^{-1}d([t]_{m}^{n}(c_{0},\ldots ,c_{m-1}))\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{1},\end{eqnarray}$$

noting $[1+t^{p^{m-1}n}]_{m}$ is a unit of $W_{m}{\mathcal{O}}_{X}$ .

The surjectivity of $1-F$ as pro-systems follows by the same argument as in the proof of [Ill79, I, Proposition 3.26]. Indeed, the formula $dx=(F-1)(dVx+dV^{2}x+\cdots +dV^{m-1}x)$ implies that

$$\begin{eqnarray}dW_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r-1}\subset (1-F)(W_{m}\unicode[STIX]{x1D6FA}_{X|D_{[n/p^{m}]}}^{r}).\end{eqnarray}$$

Therefore it is enough to show that

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{n}}^{r}\xrightarrow[{}]{1-F}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{n}}^{r}/dW_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r-1}\end{eqnarray}$$

is surjective.

Theorem 2.2.2 implies that $W_{m}\unicode[STIX]{x1D6FA}_{X|D_{n}}^{r}/dW_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r-1}$ is generated by sections

$$\begin{eqnarray}V^{i}[x]_{m-i}d\log [y_{1}]_{m}\cdots d\log [y_{r}]_{m}\quad \text{with }0\leqslant i\leqslant m-1,\end{eqnarray}$$

where $x\in {\mathcal{O}}_{X}(-D_{p^{i}\text{}\underline{n}^{\prime }})$ for some $\text{}\underline{n}^{\prime }\leqslant \text{}\underline{n}$ and $y_{j}\in {\mathcal{O}}_{X}^{\times }$ for $1\leqslant j\leqslant r$ such that

$$\begin{eqnarray}d\log [y_{1}]_{m}\cdots d\log [y_{r}]_{m}\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}-\text{}\underline{n}^{\prime }}}^{r}.\end{eqnarray}$$

(Note that in view of (2.3.1), $d\log [y_{i}]_{m}$ may also contribute to the multiplicity.) We may then choose (étale locally) $y\in {\mathcal{O}}_{X}(-D_{p^{i}\text{}\underline{n}^{\prime }})$ such that $y^{p}-y=x$ . Then we have

$$\begin{eqnarray}(1-F)\big(V^{i}[y]_{m-i}d\log [y_{1}]_{m}\cdots d\log [y_{r}]_{m}\big)=V^{i}[x]_{m-i}d\log [y_{1}]_{m}\cdots d\log [y_{r}]_{m},\end{eqnarray}$$

which implies the desired surjectivity.

Finally we show the exactness in the middle. It suffices to show the following equality in $W_{m}\unicode[STIX]{x1D6FA}_{X}^{r}$ :

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\cap W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r}=W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}},\log }^{r}.\end{eqnarray}$$

We prove this by induction on $m$ . For $m=1$ , this is Theorem 1.2.1.

Let $x\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\cap W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{r}$ , then we have

$$\begin{eqnarray}Rx=Fx\in W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p\text{}\underline{n}}}^{r}\cap W_{m-1}\unicode[STIX]{x1D6FA}_{X,\log }^{r}.\end{eqnarray}$$

By induction hypothesis, we have

$$\begin{eqnarray}Rx=Fx\in W_{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}},\log }^{r}.\end{eqnarray}$$

On the other hand, there is a commutative diagram

where the lower sequence is exact by [CSS83, Lemma 3]. Hence there exist $y\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}},\log }^{r}$ and $z\in \unicode[STIX]{x1D6FA}_{X,\log }^{r}$ , such that $x-y=\text{}\underline{p}^{m-1}\cdot z$ .

Since $\text{}\underline{p}^{m-1}\cdot z=x-y\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ , Corollary 2.2.7 implies $z\in \unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}$ . By Theorem 1.2.1, this implies $z\in \unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}},\log }^{r}$ and hence $\text{}\underline{p}^{m-1}\cdot z\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}},\log }^{r}$ (cf. Theorem 1.1.6). This proves $x=y+\text{}\underline{p}^{m-1}\cdot z\in W_{m}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}},\log }^{r}$ as desired.◻

3 The pairing on the relative logarithmic de Rham–Witt sheaves

Let $X,D,j:U{\hookrightarrow}X$ be as in § 2. In the following we want to define a pairing between cohomology group of $W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r}$ and cohomology group of “ $\mathop{\varprojlim }\nolimits_{D}$ ” $W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}$ . In order to define a pairing on the sheaves level, we have to write $W_{n}\unicode[STIX]{x1D6FA}_{U,\log }^{r}$ as ind-system of sheaves on $X$ .

3.1 The pairing

To define our desired pairing, we will use the notation of two-term complexes. We briefly recall the definition. In [Mil86], Milne defined a pairing of two-term complexes as follows.

Let

$$\begin{eqnarray}\mathscr{F}^{\bullet }=(\mathscr{F}^{0}\xrightarrow[{}]{d_{\mathscr{ F}}}\mathscr{F}^{1}),\quad \mathscr{G}^{\bullet }=(\mathscr{G}^{0}\xrightarrow[{}]{d_{\mathscr{ G}}}\mathscr{G}^{1})\end{eqnarray}$$

and

$$\begin{eqnarray}\mathscr{H}^{\bullet }=(\mathscr{H}^{0}\xrightarrow[{}]{d_{\mathscr{ H}}}\mathscr{H}^{1})\end{eqnarray}$$

be two-term complexes. A pairing of two-term complexes

$$\begin{eqnarray}\mathscr{F}^{\bullet }\times \mathscr{G}^{\bullet }\rightarrow \mathscr{H}^{\bullet }\end{eqnarray}$$

is a system of pairings

$$\begin{eqnarray}\displaystyle \langle \,,\rangle _{0,0}^{0}:\mathscr{F}^{0}\times \mathscr{G}^{0}\rightarrow \mathscr{H}^{0}; & & \displaystyle \nonumber\\ \displaystyle \langle \,,\rangle _{0,1}^{1}:\mathscr{F}^{0}\times \mathscr{G}^{1}\rightarrow \mathscr{H}^{1}; & & \displaystyle \nonumber\\ \displaystyle \langle \,,\rangle _{1,0}^{1}:\mathscr{F}^{1}\times \mathscr{G}^{0}\rightarrow \mathscr{H}^{1}, & & \displaystyle \nonumber\end{eqnarray}$$

such that

(3.1.1) $$\begin{eqnarray}d_{\mathscr{H}}(\langle x,y\rangle _{0,0}^{0})=\langle x,d_{\mathscr{ G}}(y)\rangle _{0,1}^{1}+\langle d_{\mathscr{ F}}(x),y\rangle _{1,0}^{1}\end{eqnarray}$$

for all $x\in \mathscr{F}^{0}$ , $y\in \mathscr{G}^{0}$ . Such a pairing is the same as a mapping

$$\begin{eqnarray}\mathscr{F}^{\bullet }\otimes \mathscr{G}^{\bullet }\rightarrow \mathscr{H}^{\bullet }.\end{eqnarray}$$

In our situation, for any tuple of integers $\text{}\underline{n}\geqslant \text{}\underline{1}$ we set

(3.1.2) $$\begin{eqnarray}W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet }:=[Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}\xrightarrow[{}]{1-C}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}],\end{eqnarray}$$

where $Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}:=j_{\ast }Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}\cap W_{m}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}$ with $j:U\rightarrow X$ the canonical map and

$$\begin{eqnarray}Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}:=\operatorname{Image}(F:W_{m+1}\unicode[STIX]{x1D6FA}_{U}^{r}\rightarrow W_{m}\unicode[STIX]{x1D6FA}_{U}^{r})\stackrel{(2.2.4)}{=}\text{Ker}(F^{m-1}d:W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}\rightarrow \unicode[STIX]{x1D6FA}_{U}^{r+1}),\end{eqnarray}$$

and $C$ is the higher Cartier map [Kat85, § 4]:

$$\begin{eqnarray}C:Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}/dV^{m-1}\unicode[STIX]{x1D6FA}_{U}^{r-1}\xrightarrow[{}]{\cong }W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}.\end{eqnarray}$$

We also set

(3.1.3) $$\begin{eqnarray}\displaystyle & \displaystyle W_{m}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet }:=[W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}\xrightarrow[{}]{1-F}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}/dV^{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}}}^{d-r-1}], & \displaystyle\end{eqnarray}$$

(3.1.4) $$\begin{eqnarray}\displaystyle & \displaystyle W_{m}\mathscr{H}^{\bullet }:=[W_{m}\unicode[STIX]{x1D6FA}_{X}^{d}\xrightarrow[{}]{1-C}W_{m}\unicode[STIX]{x1D6FA}_{X}^{d}]. & \displaystyle\end{eqnarray}$$

By [Mil86, Lemma 1.1] we have a canonical isomorphism

(3.1.5) $$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d}[0]\simeq W_{m}\mathscr{H}^{\bullet }.\end{eqnarray}$$

Lemma 3.1.1. For any tuple of integers $\text{}\underline{n}\geqslant \text{}\underline{1}$ we have a natural pairing of two-term complexes

(3.1.6) $$\begin{eqnarray}W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet }\times W_{m}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet }\rightarrow W_{m}\mathscr{H}^{\bullet }.\end{eqnarray}$$

Proof. By the definition of filtered de Rham–Witt complexes, the cup product induces pairings

$$\begin{eqnarray}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}\times W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}\rightarrow W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{1}}}^{d}\subset W_{m}\unicode[STIX]{x1D6FA}_{X}^{d}\end{eqnarray}$$

and

$$\begin{eqnarray}Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}\times W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}\rightarrow W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{1}}}^{d}\subset W_{m}\unicode[STIX]{x1D6FA}_{X}^{d}.\end{eqnarray}$$

By composing with the higher Cartier operators, we have the following pairing:

$$\begin{eqnarray}Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}\times W_{m}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}/dV^{m-1}\unicode[STIX]{x1D6FA}_{X|D_{p^{m-1}\text{}\underline{n}}}^{d-r-1}\rightarrow W_{m}\unicode[STIX]{x1D6FA}_{X}^{d};\quad (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\mapsto -C(\unicode[STIX]{x1D6FC}\wedge \unicode[STIX]{x1D6FD}).\end{eqnarray}$$

It is easy to see that these pairings are compatible. ◻

If we now let $\text{}\underline{n}$ run over $\mathbb{N}^{\unicode[STIX]{x1D6EC}}$ , we get a pairing between an ind-object and a pro-object

(3.1.7)

or equivalently, a morphism in the category of pro-objects of complexes of abelian sheaves

where $W_{m}\mathscr{H}^{\bullet }$ is viewed as a constant pro-object.

Remark 3.1.2. To construct the pairing (3.1.7) in a more natural way, we could use a full subcategory of the ind-category of pro-objects of coherent complexes (cf. [Kat00, § 2.1]).

4 Duality over finite fields

In this section we assume that the base field $k$ is finite. By taking hypercohomology groups of the pairing (3.1.7) using (3.1.5), we get a pairing

$$\begin{eqnarray}\underset{n}{\varinjlim }\,\mathbb{H}^{i}(X,W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet })\times \underset{n}{\varprojlim }\,\mathbb{H}^{d+1-i}(X,W_{m}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet })\rightarrow \mathbb{H}^{d+1}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d}).\end{eqnarray}$$

Note that there is an isomorphism in the bounded derived category $D^{b}(X,\mathbb{Z}/p^{m}\mathbb{Z})$ of étale $\mathbb{Z}/p^{m}\mathbb{Z}$ -modules:

$$\begin{eqnarray}\underset{n}{\varinjlim }\,W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet }=[j_{\ast }Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}\xrightarrow[{}]{1-C}j_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}]\cong Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r},\end{eqnarray}$$

where the second isomorphism comes from the fact that $j$ is affine. Hence we get

$$\begin{eqnarray}\underset{n}{\varinjlim }\,\mathbb{H}^{i}(X,W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet })\cong H^{i}(U,W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r})\quad \text{for any}\;i\in \mathbb{Z}.\end{eqnarray}$$

Theorem 2.3.1 implies that

(4.1.1) $$\begin{eqnarray}\underset{n}{\varprojlim }\,\mathbb{H}^{d+1-i}(X,W_{m}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet })\cong \underset{D}{\varprojlim }\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}).\end{eqnarray}$$

Combining these facts, we obtain the following corollary.

Corollary 4.1.1. We have a natural pairing of abelian groups

(4.1.2) $$\begin{eqnarray}H^{i}(U,W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r})\times \underset{D}{\varprojlim }\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})\rightarrow H^{d+1}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d})\xrightarrow[{}]{\text{Tr}}\mathbb{Z}/p^{m}\mathbb{Z},\end{eqnarray}$$

where the trace map is the canonical trace map of logarithmic de Rham–Witt sheaves (cf. [Mil86, Corollary 1.12]).

Noting that $H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})$ are finite, we can endow $\mathop{\varprojlim }\nolimits_{D}\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})$ with the inverse limit topology, i.e, the profinite topology.

Proposition 4.1.2. The pairing is continuous if we endow $H^{i}(U,W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r})$ with the discrete topology and $\mathop{\varprojlim }\nolimits_{D}\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})$ with the profinite topology.

Proof. It suffices to show that the annihilator of each $\unicode[STIX]{x1D6FC}\in H^{i}(U,W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r})$ is open in the projective limit $\mathop{\varprojlim }\nolimits_{D}\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})$ . This follows directly from the lemma below.◻

Lemma 4.1.3. For any $\unicode[STIX]{x1D6FC}\in H^{i}(U,W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r})$ , the morphism induced by (4.1.2)

$$\begin{eqnarray}\langle \unicode[STIX]{x1D6FC},\cdot \rangle :\underset{D}{\varprojlim }\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})\rightarrow H^{d+1}(X,W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d})\end{eqnarray}$$

factors through $H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})$ for some $D\in \unicode[STIX]{x1D6F4}$ .

Proof. This follows directly by the construction of the pairing. ◻

Our main result in this section is the following duality theorem.

Theorem 4.1.4. The pairing (4.1.2) is a perfect pairing of topological $\mathbb{Z}/p^{m}\mathbb{Z}$ -modules, i.e, it induces an isomorphism of profinite groups

$$\begin{eqnarray}\underset{D}{\varprojlim }\,H^{d+1-i}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r})\xrightarrow[{}]{\cong }H^{i}(U,W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r})^{\vee },\end{eqnarray}$$

where $A^{\vee }$ is the Pontryagin dual of a discrete group $A$ .

The proof is divided into two steps, the first step is to reduce the theorem to the case where $m=1$ ; then we prove this special case in the second step.

Proof. Step 1. We have the following commutative diagram with exact rows

where the first row is induced by Theorem 1.1.6, and it is exact since the inverse limit is exact for projective system of finite groups. The exactness of the second row is clear. Using this commutative diagram and induction on $m$ , we reduce our question to the case $m=1$ .

Step 2. For $m=1$ the pairing (3.1.6) is identified with

$$\begin{eqnarray}[Z\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}\xrightarrow[{}]{1-C}\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}]\times [\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}\xrightarrow[{}]{F-1}\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}/d\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r-1}]\rightarrow [\unicode[STIX]{x1D6FA}_{X}^{d}\xrightarrow[{}]{1-C}\unicode[STIX]{x1D6FA}_{X}^{d}],\end{eqnarray}$$

where for any $\text{}\underline{n}=(n_{\unicode[STIX]{x1D706}})_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}\in \mathbb{N}^{\unicode[STIX]{x1D6EC}}$ (cf. the notation in (3.1.2)),

$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}=\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)\otimes {\mathcal{O}}_{X}(-D_{\text{}\underline{n}}), & \displaystyle \nonumber\\ \displaystyle & Z\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}=\text{Ker}(d:\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{r}\rightarrow j_{\ast }\unicode[STIX]{x1D6FA}_{U}^{r+1}),\quad d\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{d-r-1}=\operatorname{Image}(d:\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}}}^{d-r-1}\rightarrow \unicode[STIX]{x1D6FA}_{X}^{d-r}). & \displaystyle \nonumber\end{eqnarray}$$

The perfectness of the pairings

(4.1.3) $$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{X}^{r}(\log D)\otimes \unicode[STIX]{x1D6FA}_{X}^{d-r}(\log D)(-D)\rightarrow \unicode[STIX]{x1D6FA}_{X}^{d}(\log D)(-D)=\unicode[STIX]{x1D6FA}_{X}^{d}\end{eqnarray}$$

implies that the following pairings

(4.1.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r} & \otimes & \displaystyle \unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}\rightarrow \unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{1}}}^{d}=\unicode[STIX]{x1D6FA}_{X}^{d},\quad (\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\mapsto \unicode[STIX]{x1D709}\wedge \unicode[STIX]{x1D702};\end{eqnarray}$$

(4.1.5) $$\begin{eqnarray}\displaystyle Z\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r} & \otimes & \displaystyle \unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}/d\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r-1}\rightarrow \unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{1}}}^{d}=\unicode[STIX]{x1D6FA}_{X}^{d},\quad (\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\mapsto -C(\unicode[STIX]{x1D709}\wedge \unicode[STIX]{x1D702});\end{eqnarray}$$

are perfect. In fact the perfectness of the pairing (4.1.5) follows from [Mil76, Lemma 1.7].

By Grothendieck–Serre duality, we obtain the following isomorphisms as $k$ -vector spaces:

$$\begin{eqnarray}H^{i}(X,\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r})\cong H^{d-i}(X,\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r})^{\ast },\end{eqnarray}$$

and

$$\begin{eqnarray}H^{i}(X,Z\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r})\cong H^{d-i}(X,\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}/d\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r-1})^{\ast }.\end{eqnarray}$$

Note that, for any two $k$ -vector spaces $V$ and $W$ , an isomorphism of $k$ -vector spaces

$$\begin{eqnarray}W\cong \text{Hom}_{k}(V,k)=:V^{\ast }\end{eqnarray}$$

uniquely corresponds to an isomorphism of $\mathbb{F}_{p}$ -vector spaces

$$\begin{eqnarray}W\cong \text{Hom}_{\mathbb{F}_{p}}(V,\mathbb{F}_{p})=:V^{\vee }.\end{eqnarray}$$

The above two isomorphisms give the isomorphism $(1)$ in the following commutative diagram

where the isomorphism (2) is induced by Theorem 1.2.1, (3) follows from the observation that $j_{\ast }\unicode[STIX]{x1D6FA}_{U}^{r}=\mathop{\varinjlim }\nolimits_{\text{}\underline{n}}\,\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r}$ , and the isomorphism (4) is due to the fact that $Rj_{\ast }\unicode[STIX]{x1D6FA}_{U,\log }^{r}\cong [j_{\ast }Z\unicode[STIX]{x1D6FA}_{U}^{r}\xrightarrow[{}]{1-C}j_{\ast }\unicode[STIX]{x1D6FA}_{U}^{r}]$ . Therefore the last horizontal map is an isomorphism.◻

In particular, for $i=1$ and $r=0$ we get isomorphisms

$$\begin{eqnarray}\underset{D}{\varprojlim }\,H^{d}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d})\xrightarrow[{}]{\cong }H^{1}(U,\mathbb{Z}/p^{m}\mathbb{Z})^{\vee }\cong \unicode[STIX]{x1D70B}_{1}^{ab}(U)/p^{m},\end{eqnarray}$$

and

$$\begin{eqnarray}H^{1}(U,\mathbb{Z}/p^{m}\mathbb{Z})\xrightarrow[{}]{\cong }\underset{D}{\varinjlim }\,H^{d}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d})^{\vee }.\end{eqnarray}$$

These isomorphisms can be used to define a measure of ramification for étale abelian covers of $U$ whose degree divides $p^{m}$ .

Definition 4.1.5. For any $D\in \unicode[STIX]{x1D6F4}$ , we define

$$\begin{eqnarray}\displaystyle & \displaystyle \text{Fil}_{D}H^{1}(U,\mathbb{Z}/p^{m}\mathbb{Z}):=H^{d}(X,W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d})^{\vee }, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \text{Fil}_{D}H^{1}(U,\mathbb{Q}/\mathbb{Z}):=H^{1}(U,\mathbb{Q}/\mathbb{Z})\{p^{\prime }\}\bigoplus \mathop{\bigcup }_{m\geqslant 1}\text{Fil}_{D}H^{1}(U,\mathbb{Z}/p^{m}\mathbb{Z}), & \displaystyle \nonumber\end{eqnarray}$$

where $H^{1}(U,\mathbb{Q}/\mathbb{Z})\{p^{\prime }\}$ is the prime-to- $p$ part of $H^{1}(U,\mathbb{Q}/\mathbb{Z})$ . Dually we define

$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70B}_{1}^{\text{ab}}(X,D)/p^{m}:=\text{Hom}(\text{Fil}_{D}H^{1}(U,\mathbb{Z}/p^{m}\mathbb{Z}),\mathbb{Z}/p^{m}\mathbb{Z}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70B}_{1}^{\text{ab}}(X,D):=\text{Hom}(\text{Fil}_{D}H^{1}(U,\mathbb{Q}/\mathbb{Z}),\mathbb{Q}/\mathbb{Z}). & \displaystyle \nonumber\end{eqnarray}$$

The group $\unicode[STIX]{x1D70B}_{1}^{\text{ab}}(X,D)/p^{m}$ is a quotient of $\unicode[STIX]{x1D70B}_{1}^{\text{ab}}(U)/p^{m}$ , which can be thought of as classifying abelian étale coverings of $U$ whose degree divides $p^{m}$ with ramification bounded by $D$ . These groups are important objects in higher-dimensional class field theory.

5 Duality over perfect fields

When the base field $k$ is finite, our duality theory is formulated by endowing the cohomology groups with the structure of topological groups. When the base field $k$ is not finite, it is necessary to endow the cohomology groups with stronger structures, namely the structures of proalgebraic and indalgebraic groups, and use Breen–Serre duality instead of Pontryagin duality. In this section, $k$ denotes a perfect field of characteristic $p>0$ , not necessarily finite, and we put $S=\text{Spec}(k)$ .

5.1 The relative perfect étale site

Recall a scheme $T$ is said to be perfect if the absolute Frobenius morphism $F:T\rightarrow T$ is an isomorphism. For any $S$ -scheme $X$ , the perfection $X^{\text{pf}}$ of $X$ is the projective limit of the system

$$\begin{eqnarray}X_{\text{red}}\xleftarrow[{}]{F}X_{\text{red}}^{(p^{-1})}\xleftarrow[{}]{F}\cdots \xleftarrow[{}]{F}X_{\text{red}}^{(p^{-n})}\xleftarrow[{}]{F}\cdots \,,\end{eqnarray}$$

where $X_{\text{red}}^{(p^{-n})}$ is the scheme $X_{\text{red}}$ with the structure map $F^{n}\circ \unicode[STIX]{x1D70B}:X\rightarrow S$ . It is a perfect scheme, and has the universal property that

$$\begin{eqnarray}\text{Hom}_{S}(X,Y)=\text{Hom}_{S}(X^{\text{pf}},Y)\end{eqnarray}$$

for any perfect $S$ -scheme $Y$ . A perfect $S$ -scheme $X$ is said to be algebraic if it is the perfection of a scheme of finite type over $S$ . One sees easily that the perfect algebraic group schemes over $S$ form an abelian category. Let $(\mathit{Pf}/S)_{\acute{\text{e}}\text{t}}$ be the perfect étale site over $S$ , i.e., the category of perfect schemes over $S$ with étale topology.

In what follows we fix a smooth proper morphism $\unicode[STIX]{x1D70B}:X\rightarrow S$ and an effective divisor $D$ such that Supp( $D$ ) is a simple normal crossing divisor on $X$ . Let $j:U:=X-D{\hookrightarrow}X$ be the complement of $D$ . Let $(\mathit{Pf}X/S)_{\acute{\text{e}}\text{t}}$ be the relative perfect étale site over $X/S$ , i.e., the category of pairs $(T,Y)$ , where $T$ is a perfect scheme over $S$ and $Y$ is étale over $X\times _{S}T$ equipped with étale topology. We define $\mathscr{X}$ and $\mathscr{S}$ to be the category of abelian sheaves on $(\mathit{Pf}X/S)_{\acute{\text{e}}\text{t}}$ and on $(\mathit{Pf}/S)_{\acute{\text{e}}\text{t}}$ , respectively. For any integer $m\geqslant 1$ , we denote $\mathscr{X}(p^{m})$ (respectively $\mathscr{S}(p^{m})$ ) to be the category of sheaves of $\mathbb{Z}/p^{m}\mathbb{Z}$ -modules on $(\mathit{Pf}X/S)_{\acute{\text{e}}\text{t}}$ (respectively $(\mathit{Pf}/S)_{\acute{\text{e}}\text{t}}$ ). The structure morphism $\unicode[STIX]{x1D70B}:X\rightarrow S$ induces a morphism of sites

$$\begin{eqnarray}\unicode[STIX]{x1D70B}:(\mathit{Pf}X/S)_{\acute{\text{e}}\text{t}}\rightarrow (\mathit{Pf}/S)_{\acute{\text{e}}\text{t}},\quad (T,Y)\mapsto T,\end{eqnarray}$$

which gives rise to adjoint functors

Definition 1.1.1 gives an object $W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ of $\mathscr{X}(p^{m})$ such that $R^{i}\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{r}$ is the sheaf on $(\mathit{Pf}/S)_{\acute{\text{e}}\text{t}}$ associated to the presheaf

$$\begin{eqnarray}T\mapsto H^{i}(X_{T},W_{m}\unicode[STIX]{x1D6FA}_{X_{T}|D_{T},\log }^{r})\quad (T\in Ob((\mathit{Pf}/S)_{\acute{\text{e}}\text{t}})).\end{eqnarray}$$

5.2 Duality theorem

By (3.1.2) we have an isomorphism

$$\begin{eqnarray}\underset{\text{}\underline{n}}{\varinjlim }\,W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet }=[j_{\ast }Z_{1}W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}\xrightarrow[{}]{1-C}j_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U}^{r}]\cong Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r},\end{eqnarray}$$

where the second isomorphism follows from the fact that $j$ is affine. Therefore

(5.2.1) $$\begin{eqnarray}R\,\underset{\text{}\underline{n}}{\varinjlim }\,R\unicode[STIX]{x1D70B}_{\ast }W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet }=R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r}\in D^{b}(\mathscr{S}(p^{m})),\end{eqnarray}$$

since $R\,\mathop{\varinjlim }\nolimits_{\text{}\underline{n}}$ commutes with $R\unicode[STIX]{x1D70B}_{\ast }$ . By (3.1.6) and (3.1.5), we have a map

$$\begin{eqnarray}R\unicode[STIX]{x1D70B}_{\ast }W_{m}{\mathcal{G}}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet }\rightarrow R{\mathcal{H}}om_{\mathscr{ S}}(R\unicode[STIX]{x1D70B}_{\ast }W_{m}{\mathcal{F}}_{-\text{}\underline{n}}^{r,\bullet },R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d}).\end{eqnarray}$$

By taking the homotopy limit $R\,\mathop{\varprojlim }\nolimits_{\text{}\underline{n}}$ on both sides, we obtain a map

$$\begin{eqnarray}\displaystyle R\,\underset{\text{}\underline{n}}{\varprojlim }\,R\unicode[STIX]{x1D70B}_{\ast }W_{m}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet } & \rightarrow & \displaystyle R\,\underset{\text{}\underline{n}}{\varprojlim }\,R{\mathcal{H}}om_{\mathscr{S}}(R\unicode[STIX]{x1D70B}_{\ast }W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet },R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d})\nonumber\\ \displaystyle & \simeq & \displaystyle R{\mathcal{H}}om_{\mathscr{S}}\biggl(R\,\underset{\text{}\underline{n}}{\varinjlim }\,R\unicode[STIX]{x1D70B}_{\ast }W_{m}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet },R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d}\biggr)\nonumber\\ \displaystyle & \simeq & \displaystyle R{\mathcal{H}}om_{\mathscr{S}}(R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r},R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d})\nonumber\\ \displaystyle & \rightarrow & \displaystyle R{\mathcal{H}}om_{\mathscr{S}}(R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r},\mathbb{Z}/p^{m}\mathbb{Z})[-d]\nonumber\end{eqnarray}$$

where the second isomorphism follows from (5.2.1) and the last map is induced by the trace map $\text{Tr}:R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X,\log }^{d}\rightarrow \mathbb{Z}/p^{m}\mathbb{Z}[-d]$ . Thus Theorem 2.3.1 gives rise to a map

(5.2.2) $$\begin{eqnarray}R\,\underset{D}{\varprojlim }\,R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}\rightarrow R{\mathcal{H}}om_{\mathscr{ S}(p^{m})}(R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r},\mathbb{Z}/p^{m}\mathbb{Z})[-d].\end{eqnarray}$$

Theorem 5.2.1. The map (5.2.2) is an isomorphism in $D^{b}(\mathscr{S}(p^{m}))$ .

Proof. By the same method as in the proof of Theorem 4.1.4, we reduce the claim to the case $m=1$ . We then use the following result from [Mil76, Proposition 2.1], [Ber81, Lemma 3.6].

Proposition 5.2.2. Let $\mathscr{L}$ be a locally free ${\mathcal{O}}_{X}$ -module of finite rank and put $\mathscr{L}^{\vee }={\mathcal{H}}om_{{\mathcal{O}}_{X}}(\mathscr{L},{\mathcal{O}}_{X})$ . Then the natural pairing

$$\begin{eqnarray}\mathscr{L}\times (\mathscr{L}^{\vee }\otimes \unicode[STIX]{x1D6FA}_{X}^{d})\rightarrow [\unicode[STIX]{x1D6FA}_{X}^{d}\xrightarrow[{}]{1-C}\unicode[STIX]{x1D6FA}_{X}^{d}][1]\cong \unicode[STIX]{x1D6FA}_{X,\log }^{d}[1]\end{eqnarray}$$

and the trace map $R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{X,\log }^{d}\rightarrow \mathbb{Z}/p\mathbb{Z}[-d]$ induces an isomorphism

$$\begin{eqnarray}R\unicode[STIX]{x1D70B}_{\ast }\mathscr{L}\xrightarrow[{}]{\cong }R{\mathcal{H}}om_{\mathscr{S}(p)}(R\unicode[STIX]{x1D70B}_{\ast }(\mathscr{L}^{\vee }\otimes \unicode[STIX]{x1D6FA}_{X}^{d}),\mathbb{Z}/p\mathbb{Z})[-d+1].\end{eqnarray}$$

Corollary 5.2.3. The perfect pairings (4.1.4) and (4.1.5) induce isomorphisms

$$\begin{eqnarray}\displaystyle & R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}\xrightarrow[{}]{\cong }R{\mathcal{H}}om_{\mathscr{S}(p)}(R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r},\mathbb{Z}/p\mathbb{Z})[-d+1]; & \displaystyle \nonumber\\ \displaystyle & R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r}/d\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}}}^{d-r-1}\xrightarrow[{}]{\cong }R{\mathcal{H}}om_{\mathscr{S}(p)}(R\unicode[STIX]{x1D70B}_{\ast }Z\unicode[STIX]{x1D6FA}_{X|D_{-\text{}\underline{n}}}^{r},\mathbb{Z}/p\mathbb{Z})[-d+1]. & \displaystyle \nonumber\end{eqnarray}$$

Therefore, we have an isomorphism

$$\begin{eqnarray}R\unicode[STIX]{x1D70B}_{\ast }W_{1}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{\bullet }\xrightarrow[{}]{\cong }R{\mathcal{H}}om_{\mathscr{ S}(p)}(R\unicode[STIX]{x1D70B}_{\ast }W_{1}\mathscr{F}_{-\text{}\underline{n}}^{\bullet },\mathbb{Z}/p\mathbb{Z})[-d],\end{eqnarray}$$

where $W_{1}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet }$ and $W_{1}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet }$ were defined in (3.1.2) and (3.1.3).

Proof of Theorem 5.2.1(continued).

By taking the limit, we obtain

$$\begin{eqnarray}\displaystyle R\,\underset{D}{\varprojlim }\,R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r} & \xrightarrow[{}]{\cong } & \displaystyle R\,\underset{\text{}\underline{n}}{\varprojlim }\,R\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D6FA}_{X|D_{\text{}\underline{n}+\text{}\underline{1}},\log }^{d-r}\xrightarrow[{}]{\cong }R\,\underset{\text{}\underline{n}}{\varprojlim }\,R\unicode[STIX]{x1D70B}_{\ast }W_{1}\mathscr{G}_{\text{}\underline{n}+\text{}\underline{1}}^{d-r,\bullet }\nonumber\\ \displaystyle & \xrightarrow[{}]{\cong } & \displaystyle R\,\underset{\text{}\underline{n}}{\varprojlim }\,R{\mathcal{H}}om_{\mathscr{S}(p)}(R\unicode[STIX]{x1D70B}_{\ast }W_{1}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet },\mathbb{Z}/p\mathbb{Z})[-d]\nonumber\\ \displaystyle & \xrightarrow[{}]{\cong } & \displaystyle R{\mathcal{H}}om_{\mathscr{S}(p)}(R\,\underset{\text{}\underline{n}}{\varinjlim }\,R\unicode[STIX]{x1D70B}_{\ast }W_{1}\mathscr{F}_{-\text{}\underline{n}}^{r,\bullet },\mathbb{Z}/p\mathbb{Z})[-d]\nonumber\\ \displaystyle & \xrightarrow[{}]{\cong } & \displaystyle R{\mathcal{H}}om_{\mathscr{S}(p)}(R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }\unicode[STIX]{x1D6FA}_{U,\log }^{r},\mathbb{Z}/p\mathbb{Z})[-d].\nonumber\end{eqnarray}$$

This is our theorem in the case that $m=1$ .◻

Remark 5.2.4. In fact we can endow $R\,\mathop{\varprojlim }\nolimits_{D}\,R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}$ with a structure of a complex of proalgebraic groups, i.e., as an object in the bounded derived category of quasi-unipotent proalgebraic groups, and similarly view $R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r}$ as an object in the bounded derived category of quasi-unipotent indalgebraic groups. Then Theorem 5.2.2 identifies $R\,\mathop{\varprojlim }\nolimits_{D}\,R\unicode[STIX]{x1D70B}_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{X|D,\log }^{d-r}$ with the Breen–Serre dual of $R\unicode[STIX]{x1D70B}_{\ast }Rj_{\ast }W_{m}\unicode[STIX]{x1D6FA}_{U,\log }^{r}$ (cf. [Pép14, § 2.5]).