Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-03T19:12:53.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformation spaces and normal forms around transversals

Part of: Symplectic geometry, contact geometry Global differential geometry

Published online by Cambridge University Press:  17 February 2020

Francis Bischoff ,
Henrique Bursztyn ,
Hudson Lima  and
Eckhard Meinrenken
Francis Bischoff
Affiliation:
Mathematical Institute and Exeter College, University of Oxford, Oxford, OX2 6GG, UK email [email protected]
Henrique Bursztyn
Affiliation:
IMPA, Estrada Dona Castorina 110, Rio de Janeiro, 22460-320, Brazil email [email protected]
Hudson Lima
Affiliation:
Departamento de Matemática – UFPR, Centro Politécnico, Curitiba, 81531-980, Brazil email [email protected]
Eckhard Meinrenken
Affiliation:
Department of Mathematics, University of Toronto, 40 St. George Street, Toronto, Ontario, CanadaM5S 2E4 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a manifold 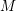$M$ with a submanifold 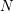$N$, the deformation space 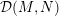${\mathcal{D}}(M,N)$ is a manifold with a submersion to 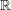$\mathbb{R}$ whose zero fiber is the normal bundle 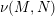$\unicode[STIX]{x1D708}(M,N)$, and all other fibers are equal to 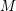$M$. This article uses deformation spaces to study the local behavior of various geometric structures associated with singular foliations, with 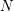$N$ a submanifold transverse to the foliation. New examples include 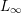$L_{\infty }$-algebroids, Courant algebroids, and Lie bialgebroids. In each case, we obtain a normal form theorem around 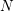$N$, in terms of a model structure over 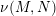$\unicode[STIX]{x1D708}(M,N)$.

Keywords

deformation spacesplitting theoremsL∞-algebroidsCourant algebroids

MSC classification

Primary: 53C15: General geometric structures on manifolds (almost complex, almost product structures, etc.)
Secondary: 53D17: Poisson manifolds; Poisson groupoids and algebroids 53D18: Generalized geometries (à la Hitchin)
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 4 , April 2020 , pp. 697 - 732
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Androulidakis, I. and Skandalis, G., The holonomy groupoid of a singular foliation, J. Reine Angew. Math. 626 (2009), 1–37.CrossRefGoogle Scholar
Androulidakis, I. and Zambon, M., Stefan-Sussmann singular foliations, singular subalgebroids and their associated sheaves, Int. J. Geom. Methods Mod. Phys. 13(suppl.) (2016), 1641001.CrossRefGoogle Scholar
Bonavolontà, G. and Poncin, N., On the category of Lie n-algebroids, J. Geom. Phys. 73 (2013), 70–90.CrossRefGoogle Scholar
Bruce, A., From L ∞-algebroids to higher Schouten/Poisson structures, Rep. Math. Phys. 67 (2011), 157–177.CrossRefGoogle Scholar
Bursztyn, H., Lima, H. and Meinrenken, E., Splitting theorems for Poisson and related structures, J. Reine Angew. Math. 754 (2019), 281–312.CrossRefGoogle Scholar
Bursztyn, H., Ponte, D. I. and Severa, P., Courant morphisms and moment maps, Math. Res. Lett. 16 (2009), 215–232.CrossRefGoogle Scholar
Cattaneo, A. and Felder, G., Relative formality theorem and quantisation of coisotropic submanifolds, Adv. Math. 208 (2007), 521–548.CrossRefGoogle Scholar
Conn, J. F., Normal forms for smooth Poisson structures, Ann. of Math. (2) 121 (1985), 565–593.CrossRefGoogle Scholar
Connes, A., Noncommutative geometry (Academic Press, San Diego, CA, 1994).Google Scholar
Crainic, M. and Fernandes, R. L., A geometric approach to Conn’s linearization theorem, Ann. of Math. (2) 173 (2011), 1121–1139.CrossRefGoogle Scholar
Dufour, J.-P., Normal forms for Lie algebroids, in Lie algebroids and related topics in differential geometry (Warsaw, 2000), Banach Center Publ., vol. 54 (Polish Acad. Sci. Inst. Math., Warsaw, 2001), 35–41.Google Scholar
Fernandes, R., Connections in Poisson geometry. I. Holonomy and invariants, J. Differential Geom. 54 (2000), 303–365.CrossRefGoogle Scholar
Frejlich, P., Submersions by Lie algebroids, J. Geom. Phys. 137 (2019), 237–246.CrossRefGoogle Scholar
Frejlich, P. and Marcut, I., The normal form theorem around Poisson transversals, Pacific J. Math. 287 (2017), 371–391.CrossRefGoogle Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), vol. 2 (Springer, Berlin, 1984).CrossRefGoogle Scholar
Garmendia, A. and Yudilevich, O., On the inner automorphisms of a singular foliation, Math. Z. 293 (2019), 725–729.CrossRefGoogle Scholar
Grabowski, J. and Jóźwikowski, M., Pontryagin maximum principle on almost Lie algebroids, SIAM J. Control Optim. 49 (2011), 1306–1357.CrossRefGoogle Scholar
Grabowski, J. and Rotkiewicz, M., Higher vector bundles and multi-graded symplectic manifolds, J. Geom. Phys. 59 (2009), 1285–1305.CrossRefGoogle Scholar
Grabowski, J. and Urbanski, P., Lie algebroids and Poisson-Nijenhuis structures, Rep. Math. Phys. 40 (1997), 195–208.CrossRefGoogle Scholar
Grützmann, M. and Xu, X., Cohomology for almost Lie algebroids, Preprint (2012), arXiv:1206.5466.Google Scholar
Haj Saeedi Sadegh, A. R. and Higson, N., Euler-like vector fields, deformation spaces and manifolds with filtered structure, Doc. Math. 23 (2018), 293–325.Google Scholar
Hermann, R., The differential geometry of foliations. II, J. Math. Mech. 11 (1962), 303–315.Google Scholar
Higgins, P. J. and Mackenzie, K., Algebraic constructions in the category of Lie algebroids, J. Algebra 129 (1990), 194–230.CrossRefGoogle Scholar
Higson, N., The tangent groupoid and the index theorem, in Quanta of maths, Clay Mathematics Proceedings, vol. 11 (American Mathematical Society, Providence, RI, 2010), 241–256.Google Scholar
Hilsum, M. and Skandalis, G., Morphismes K-orientés d’espaces de feuilles et fonctorialité en théorie de Kasparov (d’après une conjecture d’A. Connes), Ann. Sci. Éc. Norm. Supér. (4) 20 (1987), 325–390.CrossRefGoogle Scholar
Jotz Lean, M., Lie 2-algebroids and matched pairs of 2-representations: a geometric approach, Pacific J. Math. 301 (2019), 143–188.CrossRefGoogle Scholar
Kashiwara, M. and Schapira, P., Sheaves on manifolds, Grundlehren der Mathematischen Wissenschaften, vol. 292 (Springer, Berlin, 1994).Google Scholar
Laurent-Gengoux, C., Lavau, S. and Strobl, T., The universal Lie infinity-algebroid of a singular foliation, Preprint (2018), arXiv:1806.00475.Google Scholar
Li-Bland, D. and Meinrenken, E., Courant algebroids and Poisson geometry, Int. Math. Res. Not. IMRN 11 (2009), 2106–2145.Google Scholar
Lima, H., On the local structure of brackets, PhD thesis, IMPA (2017).Google Scholar
Liu, Z.-J., Weinstein, A. and Xu, P., Manin triples for Lie bialgebroids, J. Differential Geom. 45 (1997), 547–574.CrossRefGoogle Scholar
Mackenzie, K. and Xu, P., Lie bialgebroids and Poisson groupoids, Duke Math. J. 73 (1994), 415–452.CrossRefGoogle Scholar
Meinrenken, E., Lie groups and Clifford algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 58 (Springer, Heidelberg, 2013).CrossRefGoogle Scholar
Meinrenken, E., Poisson geometry from a Dirac perspective, Lett. Math. Phys. 108 (2018), 447–498.CrossRefGoogle Scholar
Monnier, P. and Zung, N. T., Levi decomposition for smooth Poisson structures, J. Differential Geom. 68 (2004), 347–395.CrossRefGoogle Scholar
Oh, Y.-G. and Park, J.-S., Deformations of coisotropic submanifolds and strong homotopy Lie algebroids, Invent. Math. 161 (2005), 287–360.CrossRefGoogle Scholar
Pym, B. and Safronov, P., Shifted symplectic Lie algebroids, Int. Math. Res. Not. IMRN (2018), rny215; doi:10.1093/imrn/rny215.CrossRefGoogle Scholar
Roytenberg, D., Courant algebroids, derived brackets and even symplectic supermanifolds, PhD thesis, UC Berkeley (1999), arXiv:math.DG/9910078.Google Scholar
Sati, H., Schreiber, U. and Stasheff, J., Twisted differential string and fivebrane structures, Comm. Math. Phys. 315 (2012), 169–213.CrossRefGoogle Scholar
S̆evera, P., Letters to Alan Weinstein, 1998–2000, available at author’s website.Google Scholar
S̆evera, P., Some title containing the words ‘homotopy’ and ‘symplectic’, e.g. this one, Travaux Mathématiques, vol. XVI (University of Luxembourg, 2005), 121–137.Google Scholar
S̆evera, P., Poisson Lie T-duality and Courant algebroids, Lett. Math. Phys. 105 (2015), 1689–1701.CrossRefGoogle Scholar
S̆evera, P. and Weinstein, A., Poisson geometry with a 3-form background, Progr. Theoret. Phys. Suppl. (2001), 145–154.CrossRefGoogle Scholar
Sheng, Y. and Zhu, C., Higher extensions of Lie algebroids, Commun. Contemp. Math. 19 (2017), 1650034.CrossRefGoogle Scholar
Stefan, P., Integrability of systems of vector fields, J. Lond. Math. Soc. (2) 21 (1980), 544–556.CrossRefGoogle Scholar
Sussmann, H., Orbits of families of vector fields and integrability of distributions, Trans. Amer. Math. Soc. 180 (1973), 171–188.CrossRefGoogle Scholar
Uchino, K., Remarks on the definition of a Courant algebroid, Lett. Math. Phys. 60 (2002), 171–175.CrossRefGoogle Scholar
Vaĭntrob, A., Lie algebroids and homological vector fields, Uspekhi Mat. Nauk 52 (1997), 161–162.Google Scholar
Voronov, T., Higher derived brackets and homotopy algebras, J. Pure Appl. Algebra 202 (2005), 133–153.CrossRefGoogle Scholar
Voronov, T., $Q$-manifolds and higher analogs of Lie algebroids, XXIX Workshop on Geometric Methods in Physics, AIP Conference Proceedings, vol. 1307 (American Institute of Physics, Melville, NY, 2010), 191–202.Google Scholar
Wang, R., On integrable systems and rigidity for PDE’s with symmetry, PhD thesis, University of Utrecht (2017), arXiv:1712.00808.Google Scholar
Weinstein, A., The local structure of Poisson manifolds, J. Differential Geom. 18 (1983), 523–557.CrossRefGoogle Scholar
Weinstein, A., Blowing up realizations of Heisenberg-Poisson manifolds, Bull. Sci. Math. 113 (1989), 381–406.Google Scholar
Weinstein, A., Almost invariant submanifolds for compact group actions, J. Eur. Math. Soc. (JEMS) 2 (2000), 53–86.CrossRefGoogle Scholar