Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T18:30:18.946Z Has data issue: false hasContentIssue false
  • English
  • Français

The 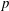$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-cyclic McKay correspondence via motivic integration

Part of: Birational geometry Algebraic number theory: local and $p$-adic fields General commutative ring theory Representation theory of groups

Published online by Cambridge University Press:  10 June 2014

Takehiko Yasuda
Takehiko Yasuda*
Affiliation:
Department of Mathematics, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the McKay correspondence for representations of the cyclic group of order 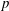$p$ in characteristic 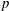$p$. The main tool is the motivic integration generalized to quotient stacks associated to representations. Our version of the change of variables formula leads to an explicit computation of the stringy invariant of the quotient variety. A consequence is that a crepant resolution of the quotient variety (if any) has topological Euler characteristic 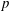$p$ as in the tame case. Also, we link a crepant resolution with a count of Artin–Schreier extensions of the power series field with respect to weights determined by ramification jumps and the representation.

Keywords

McKay correspondencemotivic integrationstringy invariantpositive characteristicArtin–Schreier extension

MSC classification

Secondary: 14E16: McKay correspondence 14E18: Arcs and motivic integration 13A50: Actions of groups on commutative rings; invariant theory 11S15: Ramification and extension theory 20C20: Modular representations and characters
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 7 , July 2014 , pp. 1125 - 1168
Copyright
© The Author 2014 

References

Artin, M., Coverings of the rational double points in characteristic p, in Complex analysis and algebraic geometry (Iwanami Shoten, Tokyo, 1977), 11–22.Google Scholar
Bădescu, L., Algebraic surfaces, Universitext (Springer, New York, 2001).Google Scholar
Batyrev, V. V., Stringy Hodge numbers of varieties with Gorenstein canonical singularities, in Integrable systems and algebraic geometry (Kobe/Kyoto, 1997) (World Scientific, River Edge, NJ, 1998), 1–32.Google Scholar
Batyrev, V. V., Non-Archimedean integrals and stringy Euler numbers of log-terminal pairs, J. Eur. Math. Soc. (JEMS) 1 (1999), 5–33.Google Scholar
Bezrukavnikov, R. V. and Kaledin, D. B., McKay equivalence for symplectic resolutions of quotient singularities, Tr. Mat. Inst. Steklova 246 (2004), 20–42 (in Algebr. Geom. Metody, Svyazi i Prilozh).Google Scholar
Bridgeland, T., King, A. and Reid, M., The McKay correspondence as an equivalence of derived categories, J. Amer. Math. Soc. 14 (2001), 535–554; (electronic).Google Scholar
Campbell, H. E. A. E. and Wehlau, D. L., Modular invariant theory, in Encyclopaedia of mathematical sciences, Vol. 139, Invariant Theory and Algebraic Transformation Groups, vol. 8 (Springer, Berlin, 2011).Google Scholar
Craw, A., An introduction to motivic integration, in Strings and geometry, Clay Mathematics Proceedings, vol. 3 (American Mathematical Society, Providence, RI, 2004), 203–225.Google Scholar
Craw, A. and Ishii, A., Flops of G-Hilb and equivalences of derived categories by variation of GIT quotient, Duke Math. J. 124 (2004), 259–307.Google Scholar
Denef, J. and Loeser, F., Germs of arcs on singular algebraic varieties and motivic integration, Invent. Math. 135 (1999), 201–232.Google Scholar
Denef, J. and Loeser, F., Motivic integration, quotient singularities and the McKay correspondence, Compositio Math. 131 (2002), 267–290.Google Scholar
Ellingsrud, G. and Skjelbred, T., Profondeur d’anneaux d’invariants en caractéristique p, Compositio Math. 41 (1980), 233–244.Google Scholar
Gonzalez-Sprinberg, G. and Verdier, J.-L., Sur la règle de McKay en caractéristique positive, C. R. Acad. Sci. Paris Sér. I Math. 301 (1985), 585–587.Google Scholar
Graham, R. L., Knuth, D. E. and Patashnik, O., A foundation for computer science, in Concrete mathematics (Addison-Wesley, Reading, MA, 1989).Google Scholar
Grayson, D. R. and Stillman, M. E., Macaulay2, a software system for research in algebraic geometry, available at http://www.math.uiuc.edu/Macaulay2/.Google Scholar
Grothendieck, A. and Dieudonné, J. A., Éléments de géométrie algébrique. I, in Grundlehren der mathematischen Wissenschaften, Vol. 166 (Springer, Berlin, 1971).Google Scholar
Harbater, D., Moduli of p-covers of curves, Comm. Algebra 8 (1980), 1095–1122.Google Scholar
Hirokado, M., Ito, H. and Saito, N., Three dimensional canonical singularities in codimension two in positive characteristic, J. Algebra 373 (2013), 207–222.Google Scholar
Kapranov, M. and Vasserot, E., Vertex algebras and the formal loop space, Publ. Math. Inst. Hautes Études Sci. 100 (2004), 209–269.Google Scholar
Kawamata, Y., Log crepant birational maps and derived categories, J. Math. Sci. Univ. Tokyo 12 (2005), 211–231.Google Scholar
Lipman, J., Rational singularities, with applications to algebraic surfaces and unique factorization, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 195–279.Google Scholar
Looijenga, E., Motivic measures, Astérisque 276 (2002), 267–297; Séminaire Bourbaki, Vol. 1999/2000.Google Scholar
Milne, J. S., Étale cohomology, Princeton Mathematical Series, vol. 33 (Princeton University Press, Princeton, NJ, 1980).Google Scholar
Nicaise, J., A trace formula for varieties over a discretely valued field, J. Reine Angew. Math. 650 (2011), 193–238.Google Scholar
Nicaise, J. and Sebag, J., The Grothendieck ring of varieties, in Motivic integration and its interactions with model theory and non-Archimedean geometry, Vol. I, London Mathematical Society Lecture Note Series, vol. 383 (Cambridge University Press, Cambridge, 2011), 145–188.Google Scholar
Reid, M., La correspondance de McKay, Astérisque 276 (2002), 53–72; Séminaire Bourbaki, Vol. 1999/2000.Google Scholar
Rose, M. A., Frobenius action on l-adic Chen–Ruan cohomology, Commun. Number Theory Phys. 1 (2007), 513–537.Google Scholar
Schröer, S., The Hilbert scheme of points for supersingular abelian surfaces, Ark. Mat. 47 (2009), 143–181.Google Scholar
Sebag, J., Intégration motivique sur les schémas formels, Bull. Soc. Math. France 132 (2004), 1–54.Google Scholar
Thomas, L., A valuation criterion for normal basis generators in equal positive characteristic, J. Algebra 320 (2008), 3811–3820.Google Scholar
Veys, W., Stringy invariants of normal surfaces, J. Algebraic Geom. 13 (2004), 115–141.Google Scholar
Yasuda, T., Twisted jets, motivic measures and orbifold cohomology, Compositio Math. 140 (2004), 396–422.Google Scholar
Yasuda, T., Motivic integration over Deligne–Mumford stacks, Adv. Math. 207 (2006), 707–761.Google Scholar
Yasuda, T., Pure subrings of regular local rings, endomorphism rings and Frobenius morphisms, J. Algebra 370 (2012), 15–31.Google Scholar
Yi, Z., Homological dimension of skew group rings and crossed products, J. Algebra 164 (1994), 101–123.Google Scholar