Article contents
A construction of complex analytic elliptic cohomology from double free loop spaces
Published online by Cambridge University Press: 26 July 2021
Abstract
We construct a complex analytic version of an equivariant cohomology theory which appeared in a paper of Rezk, and which is roughly modelled on the Borel-equivariant cohomology of the double free loop space. The construction is defined on finite, torus-equivariant CW complexes and takes values in coherent holomorphic sheaves over the moduli stack of complex elliptic curves. Our methods involve an inverse limit construction over all finite-dimensional subcomplexes of the double free loop space, following an analogous construction of Kitchloo for single free loop spaces. We show that, for any given complex elliptic curve 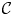 $\mathcal {C}$, the fiber of our construction over
$\mathcal {C}$, the fiber of our construction over 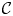 $\mathcal {C}$ is isomorphic to Grojnowski's equivariant elliptic cohomology theory associated to
$\mathcal {C}$ is isomorphic to Grojnowski's equivariant elliptic cohomology theory associated to 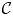 $\mathcal {C}$.
$\mathcal {C}$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 1
- Cited by



