Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T04:33:20.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing a categorical Gromov–Witten invariant

Part of: Symplectic geometry, contact geometry Surfaces and higher-dimensional varieties Abelian varieties and schemes Homological methods Projective and enumerative geometry

Published online by Cambridge University Press:  18 June 2020

Andrei Căldăraru  and
Junwu Tu
Andrei Căldăraru
Affiliation:
Mathematics Department, University of Wisconsin – Madison, 480 Lincoln Drive, Madison, WI 53706–1388, USA email [email protected]
Junwu Tu
Affiliation:
Institute of Mathematical Sciences, ShanghaiTech University, 393 Huaxia Rd, Pudong, Shanghai, 201210, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We compute the 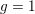$g=1$, 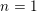$n=1$ B-model Gromov–Witten invariant of an elliptic curve 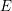$E$ directly from the derived category 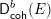$\mathsf{D}_{\mathsf{coh}}^{b}(E)$. More precisely, we carry out the computation of the categorical Gromov–Witten invariant defined by Costello using as target a cyclic 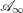$\mathscr{A}_{\infty }$ model of 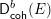$\mathsf{D}_{\mathsf{coh}}^{b}(E)$ described by Polishchuk. This is the first non-trivial computation of a positive-genus categorical Gromov–Witten invariant, and the result agrees with the prediction of mirror symmetry: it matches the classical (non-categorical) Gromov–Witten invariants of a symplectic 2-torus computed by Dijkgraaf.

Keywords

Gromov–WittenA∞ categorieselliptic curves

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Secondary: 53D37: Mirror symmetry, symplectic aspects; homological mirror symmetry; Fukaya category 14J33: Mirror symmetry 14K25: Theta functions 16E40: (Co)homology of rings and algebras (e.g. Hochschild, cyclic, dihedral, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 7 , July 2020 , pp. 1275 - 1309
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is partially supported by the National Science Foundation through grant number DMS-1200721.

References

Barannikov, S., Quantum periods I: Semi-infinite variations of Hodge structures, Int. Math. Res. Not. IMRN 23 (2001), 1243–1264.CrossRefGoogle Scholar
Bershadsky, M., Cecotti, S., Ooguri, H. and Vafa, C., Kodaira–Spencer theory of gravity and exact results for quantum string amplitudes, Commum. Math. Phys. 165 (1994), 311–427.CrossRefGoogle Scholar
Căldăraru, A., The Mukai pairing, II: The Hochschild–Kostant–Rosenberg isomorphism, Adv. Math. 194 (2005), 34–66.CrossRefGoogle Scholar
Căldăraru, A. and Willerton, S., The Mukai pairing, I: A categorical approach, New York J. Math. 16 (2010), 61–98.Google Scholar
Candelas, P., de la Ossa, X. C., Green, P. S. and Parkes, L., A pair of Calabi–Yau manifolds as an exact soluble superconformal theory, Nucl. Phys. B 359 (1991), 21–74.CrossRefGoogle Scholar
Cho, C.-H., Strong homotopy inner product of an 𝒜∞-algebra, Int. Math. Res. Not. IMRN (2008), Art. ID rnn041.Google Scholar
Costello, K., The Gromov-Witten potential associated to a TCFT, Preprint (2005), arXiv:math/0509264.Google Scholar
Costello, K., Topological conformal field theories and Calabi–Yau categories, Adv. Math. 210 (2007), 165–214.CrossRefGoogle Scholar
Costello, K., The partition function of a topological field theory, J. Topol. 2 (2009), 779–822.CrossRefGoogle Scholar
Costello, K. and Li, S., Quantum BCOV theory on Calabi–Yau manifolds and the higher genus B-model, Preprint (2012), arXiv:1201.4501.Google Scholar
Dijkgraaf, R., Mirror symmetry and elliptic curves, in The moduli space of curves, Progress in Mathematics, vol. 129 (Birkhäuser, Boston, 1995), 149–163.CrossRefGoogle Scholar
Fukaya, K., Cyclic symmetry and adic convergence in Lagrangian Floer theory, Kyoto J. Math. 50 (2010), 521–590.CrossRefGoogle Scholar
Ganatra, S., Perutz, T. and Sheridan, N., Mirror symmetry: from categories to curve counts, Preprint (2015), arXiv:1510.03839.Google Scholar
Griffiths, P., Periods of integrals on algebraic manifolds I (Construction and properties of the modular varieties), Amer. J. Math. 90 (1968), 568–626.CrossRefGoogle Scholar
Kanazawa, A. and Zhou, J., Lectures on BCOV holomorphic anomaly equations, in Calabi–Yau varieties: arithmetic, geometry and physics, Fields Institute Monograph, vol. 34 (Springer, New York, 2015), 445–473.CrossRefGoogle Scholar
Kaneko, M. and Zagier, D., A generalized Jacobi theta function and quasimodular forms, in The moduli space of curves, Progress in Mathematics, vol. 129 (Birkhäuser, Boston, 1995), 165–172.CrossRefGoogle Scholar
Kontsevich, M., Homological algebra of mirror symmetry, in Proceedings of the International Congress of Mathematicians, Vols 1, 2 (Zürich, 1994) (Birkhäuser, Basel, 1995), 120–139.CrossRefGoogle Scholar
Kontsevich, M. and Soibelman, Y., Notes on A-infinity algebras, A-infinity categories and non-commutative geometry. I, in Homological mirror symmetry, Lecture Notes in Physics, vol. 757 (Springer, Berlin, 2009), 153–219.Google Scholar
Li, S., BCOV theory on the elliptic curve and higher genus mirror symmetry, Preprint (2011), arXiv:1112.4063.Google Scholar
Li, S., Renormalization method and mirror symmetry, SIGMA 8 (2012), 101.Google Scholar
Li, S., Vertex algebras and quantum master equation, Preprint (2016), arXiv:1612.01292.Google Scholar
Penner, R. C., The decorated Teichmüller space of punctured surfaces, Commun. Math. Phys. 113 (1987), 299–339.CrossRefGoogle Scholar
Polishchuk, A., A ∞-algebra of an elliptic curve and Eisenstein series, Commun. Math. Phys. (2011), 301; 709. doi:10.1007/s00220-010-1156-y.Google Scholar
Polishchuk, A. and Zaslow, E., Categorical mirror symmetry: the elliptic curve, Adv. Theor. Math. Phys. 2 (1998), 443–470.CrossRefGoogle Scholar
Ramadoss, A., The relative Riemann–Roch theorem from Hochschild homology, New York J. Math. 14 (2008), 643–717.Google Scholar
Saito, K., Period mapping associated to a primitive form, Publ. Res. Inst. Math. Sci. 19 (1983), 1231–1264.CrossRefGoogle Scholar
Saito, K., The higher residue pairings K F(k) for a family of hypersurface singular points, in Singularities, Part 2 (Arcata, Calif., 1981) (American Mathematical Society, Providence, RI, 1983), 441–463.Google Scholar
Sen, A. and Zwiebach, B., Quantum background independence of closed-string field theory, Nuclear Phys. B 423 (1994), 580–630.CrossRefGoogle Scholar
Sheridan, N., Formulae in noncommutative Hodge theory, J. Homotopy Relat. Struct. 15 (2020), 249–299.CrossRefGoogle Scholar
Shklyarov, D., Hirzebruch–Riemann–Roch-type formula for DG algebras, Proc. Lond. Math. Soc. 106 (2013), 1–32.CrossRefGoogle Scholar
Strebel, K., Quadratic differentials (Springer, Berlin, 1984).CrossRefGoogle Scholar