Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T04:19:20.142Z Has data issue: false hasContentIssue false
  • English
  • Français

Companion forms in parallel weight one

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  10 May 2013

Toby Gee  and
Payman Kassaei
Toby Gee
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK email [email protected]
Payman Kassaei
Affiliation:
Department of Mathematics, King’s College London, London WC2R 2LS, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 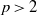$p\gt 2$ be prime, and let 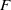$F$ be a totally real field in which 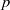$p$ is unramified. We give a sufficient criterion for a 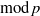$\mathrm{mod} \hspace{0.167em} p$ Galois representation to arise from a 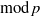$\mathrm{mod} \hspace{0.167em} p$ Hilbert modular form of parallel weight one, by proving a ‘companion forms’ theorem in this case. The techniques used are a mixture of modularity lifting theorems and geometric methods. As an application, we show that Serre’s conjecture for 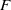$F$ implies Artin’s conjecture for totally odd two-dimensional representations over 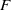$F$.

Keywords

companion formsparallel weight oneSerre’s conjecturemod p Hilbert modular forms

MSC classification

Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 6 , June 2013 , pp. 903 - 913
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F. and Goren, E. Z., Hilbert modular forms: mod $p$ and $p$-adic aspects, Mem. Amer. Math. Soc. 173 (819) (2005); MR 2110225 (2006f:11049).Google Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., Congruences between Hilbert modular forms: constructing ordinary lifts, Duke Math. J. 161 (2012), 1521–1580.Google Scholar
Barnet-Lamb, T., Gee, T. and Geraghty, D., Serre weights for rank two unitary groups, Math. Ann. (2013), doi:10.1007/s00208-012-0893-y.Google Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2), to appear.Google Scholar
Barnet-Lamb, T., Geraghty, D., Harris, M. and Taylor, R., A family of Calabi-Yau varieties and potential automorphy II, Publ. Res. Inst. Math. Sci. 47 (2011), 29–98; MR 2827723.Google Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre’s conjecture for mod $l$ Galois representations over totally real fields, Duke Math. J. 155 (2010), 105–161.CrossRefGoogle Scholar
Clozel, L., Harris, M. and Taylor, R., Automorphy for some $l$-adic lifts of automorphic mod $l$ Galois representations, Publ. Math. Inst. Hautes Études Sci. 108 (2008), 1–181.Google Scholar
Deligne, P. and Pappas, G., Singularités des espaces de modules de Hilbert, en les caractéristiques divisant le discriminant, Compositio Math. 90 (1994), 59–79; MR 1266495 (95a:11041).Google Scholar
Deligne, P. and Serre, J.-P., Formes modulaires de poids $1$, Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 507–530; MR 0379379 (52 #284).Google Scholar
Gee, T., Companion forms over totally real fields. II, Duke Math. J. 136 (2007), 275–284.CrossRefGoogle Scholar
Gee, T., Automorphic lifts of prescribed types, Math. Ann. 350 (2011), 107–144; MR 2785764 (2012c:11118).Google Scholar
Gee, T., On the weights of mod $p$ Hilbert modular forms, Invent. Math. 184 (2011), 1–46; MR 2782251.Google Scholar
Gee, T. and Geraghty, D., Companion forms for unitary and symplectic groups, Duke Math. J. 161 (2012), 247–303; MR 2876931.Google Scholar
Gross, B. H., A tameness criterion for Galois representations associated to modular forms (mod $p$), Duke Math. J. 61 (1990), 445–517; MR 1074305 (91i:11060).Google Scholar
Hida, H., On $p$-adic Hecke algebras for ${\mathrm{GL} }_{2} $ over totally real fields, Ann. of Math. (2) 128 (1988), 295–384; MR 960949 (89m:11046).Google Scholar
Katz, N. M., $p$-adic properties of modular schemes and modular forms, in Modular functions of one variable, III (Proceedings International Summer School, University of Antwerp, 1972), Lecture Notes in Mathematics, vol. 350 (Springer, Berlin, 1973), 69–190; MR 0447119 (56 #5434).Google Scholar
Khare, C., Remarks on mod $p$ forms of weight one, Int. Math. Res. Not. (1997), 127–133; MR 1434905 (97m:11070.Google Scholar
Kisin, M., Potentially semi-stable deformation rings, J. Amer. Math. Soc. 21 (2008), 513–546; MR 2373358 (2009c:11194).Google Scholar
Serre, J.-P., Sur les représentations modulaires de degré 2 de $\mathrm{Gal} ( \overline{\mathbf{Q} } / \mathbf{Q} )$, Duke Math. J. 54 (1987), 179–230; MR 885783 (88g:11022).Google Scholar
Shimura, G., The special values of the zeta functions associated with Hilbert modular forms, Duke Math. J. 45 (1978), 637–679; MR 507462 (80a:10043).Google Scholar
Thorne, J., On the automorphy of $l$-adic Galois representations with small residual image, J. Inst. Math. Jussieu 11 (2012), 855–920.Google Scholar