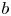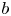The goal of this paper is to explore the cohomological consequences of the existence of moduli spaces for flat bundles with bounded rank and irregularity at infinity and to prove them unconditionally in the surface case.
Let ![]() $U$ be a smooth complex projective variety. From Simpson's work [Reference SimpsonSim94], flat bundles on
$U$ be a smooth complex projective variety. From Simpson's work [Reference SimpsonSim94], flat bundles on ![]() $U$ with given rank form a complex variety, the de Rham space of
$U$ with given rank form a complex variety, the de Rham space of ![]() $U$. If
$U$. If ![]() $U$ is quasi-projective, flat bundles acquire singularities at infinity making the situation more involved. However, regular singular flat bundles again give rise to moduli spaces at the cost of rigidifying the situation by a choice of logarithmic lattice [Reference NitsureNit93]. Let
$U$ is quasi-projective, flat bundles acquire singularities at infinity making the situation more involved. However, regular singular flat bundles again give rise to moduli spaces at the cost of rigidifying the situation by a choice of logarithmic lattice [Reference NitsureNit93]. Let ![]() $X$ be a smooth compactification of
$X$ be a smooth compactification of ![]() $U$ such that
$U$ such that ![]() $D:=X\setminus U$ has simple normal crossings and let
$D:=X\setminus U$ has simple normal crossings and let ![]() $j : U\to X$ be the inclusion. A flat bundle
$j : U\to X$ be the inclusion. A flat bundle ![]() $\mathcal {E}=(E,\nabla )$ on
$\mathcal {E}=(E,\nabla )$ on ![]() $U$ is regular singular [Reference DeligneDel70] if
$U$ is regular singular [Reference DeligneDel70] if ![]() $E$ extends to a vector bundle
$E$ extends to a vector bundle ![]() $F$ on
$F$ on ![]() $X$ with
$X$ with ![]() $\nabla (F)\subset F\otimes _{\mathcal {O}_X}\Omega ^1_X(\log D)$. Regular singularity is independent of a choice of compactification. When an extra condition on the residues is imposed,
$\nabla (F)\subset F\otimes _{\mathcal {O}_X}\Omega ^1_X(\log D)$. Regular singularity is independent of a choice of compactification. When an extra condition on the residues is imposed, ![]() $F$ is called a Deligne lattice. A natural question to ask is what lies beyond the regular singular case. In general, the connection
$F$ is called a Deligne lattice. A natural question to ask is what lies beyond the regular singular case. In general, the connection ![]() $\nabla$ no longer has simple poles at infinity, but Sabbah observed in the 1990s [Reference SabbahSab00] that
$\nabla$ no longer has simple poles at infinity, but Sabbah observed in the 1990s [Reference SabbahSab00] that ![]() $\nabla$ still has a simple expression, the so-called good formal decomposition at the cost of working formally along
$\nabla$ still has a simple expression, the so-called good formal decomposition at the cost of working formally along ![]() $D$ away from a codimension-
$D$ away from a codimension-![]() $1$ subset of
$1$ subset of ![]() $D$. The locus of
$D$. The locus of ![]() $D$ where this simple expression does not hold is the turning locus of
$D$ where this simple expression does not hold is the turning locus of ![]() $\mathcal {E}$. Away from the turning locus, Deligne's lattices admit straightforward generalizations and Malgrange proved in [Reference MalgrangeMal96] that they extend canonically to
$\mathcal {E}$. Away from the turning locus, Deligne's lattices admit straightforward generalizations and Malgrange proved in [Reference MalgrangeMal96] that they extend canonically to ![]() $X$. Armed with Deligne–Malgrange lattices and conjectural bounds for their Chern classes, it is an expectation of Esnault and Langer dating back from 2014 that there should exist a moduli of finite type for flat bundles on
$X$. Armed with Deligne–Malgrange lattices and conjectural bounds for their Chern classes, it is an expectation of Esnault and Langer dating back from 2014 that there should exist a moduli of finite type for flat bundles on ![]() $U$ with bounded rank and irregularity at infinity. See [Reference EsnaultEsn14] and [Reference KedlayaKed21, 4.3.4]. Bounded irregularity means very roughly that we bound the poles of the connection restricted to a Deligne–Malgrange lattice. See Definition 2.1 for a rigorous definition. The bound on irregularity is thus embodied by an effective divisor
$U$ with bounded rank and irregularity at infinity. See [Reference EsnaultEsn14] and [Reference KedlayaKed21, 4.3.4]. Bounded irregularity means very roughly that we bound the poles of the connection restricted to a Deligne–Malgrange lattice. See Definition 2.1 for a rigorous definition. The bound on irregularity is thus embodied by an effective divisor ![]() $R$ supported on
$R$ supported on ![]() $D$. Let us denote by
$D$. Let us denote by ![]() $\mathcal {M}_r(X,D,R)$ Esnault and Langer's expected moduli of rank-
$\mathcal {M}_r(X,D,R)$ Esnault and Langer's expected moduli of rank-![]() $r$ flat bundles on
$r$ flat bundles on ![]() $U$ with irregularity bounded by
$U$ with irregularity bounded by ![]() $R$ along
$R$ along ![]() $D$. As pointed out to the authors by Langer, there is a mismatch between Nitsure's construction and
$D$. As pointed out to the authors by Langer, there is a mismatch between Nitsure's construction and ![]() $\mathcal {M}_r(X,D,R)$ for
$\mathcal {M}_r(X,D,R)$ for ![]() $R=0$. Indeed, rigidifying the moduli problem with choices of logarithmic lattices makes Nitsure's construction depend on a choice of compactification for
$R=0$. Indeed, rigidifying the moduli problem with choices of logarithmic lattices makes Nitsure's construction depend on a choice of compactification for ![]() $X$. On the other hand, having regular singularity at infinity is independent of a choice of compactification. Furthermore, different points of Nitsure's construction may underlie the same flat bundle.
$X$. On the other hand, having regular singularity at infinity is independent of a choice of compactification. Furthermore, different points of Nitsure's construction may underlie the same flat bundle.
The existence of ![]() $\mathcal {M}_r(X,D,R)$ has deep consequences for flat bundles which can be stated and studied independently. The first consequence is cohomological. For a flat bundle
$\mathcal {M}_r(X,D,R)$ has deep consequences for flat bundles which can be stated and studied independently. The first consequence is cohomological. For a flat bundle ![]() $\mathcal {E}$ on
$\mathcal {E}$ on ![]() $U$, let
$U$, let ![]() $\operatorname {DR}\mathcal {E}$ be the algebraic de Rham complex of
$\operatorname {DR}\mathcal {E}$ be the algebraic de Rham complex of ![]() $\mathcal {E}$. Following the construction of the jumping loci for character varieties, the following subsets
$\mathcal {E}$. Following the construction of the jumping loci for character varieties, the following subsets
should form a decreasing sequence of closed subsets of ![]() $\mathcal {M}_r(X,D,R)$ when
$\mathcal {M}_r(X,D,R)$ when ![]() $j$ increases. Since
$j$ increases. Since ![]() $\mathcal {M}_r(X,D,R)$ is expected to be of finite type, its underlying topological space should be noetherian, so the sequence of
$\mathcal {M}_r(X,D,R)$ is expected to be of finite type, its underlying topological space should be noetherian, so the sequence of ![]() $\mathcal {V}^{j}$ should stabilize for
$\mathcal {V}^{j}$ should stabilize for ![]() $j$ big enough. On the other hand, de Rham cohomology is always finite dimensional. Hence, there should exist an integer
$j$ big enough. On the other hand, de Rham cohomology is always finite dimensional. Hence, there should exist an integer ![]() $j_0$ such that
$j_0$ such that ![]() $\mathcal {V}^{j_0}$ is empty. Put otherwise, there should exist a universal bound for the algebraic de Rham cohomology of rank
$\mathcal {V}^{j_0}$ is empty. Put otherwise, there should exist a universal bound for the algebraic de Rham cohomology of rank ![]() $r$ flat bundles on
$r$ flat bundles on ![]() $U$ with bounded irregularity at infinity. Furthermore, this bound should depend only on
$U$ with bounded irregularity at infinity. Furthermore, this bound should depend only on ![]() $X$,
$X$, ![]() $D$,
$D$, ![]() $R$ and
$R$ and ![]() $r$. See Conjecture 2.5 for a statement making precise the dependency in
$r$. See Conjecture 2.5 for a statement making precise the dependency in ![]() $r$ and
$r$ and ![]() $R$. One of the main results of this paper is an unconditional proof of the existence of this bound in the surface case (Theorem 6.6). To state it, we let
$R$. One of the main results of this paper is an unconditional proof of the existence of this bound in the surface case (Theorem 6.6). To state it, we let ![]() $\operatorname {Div}(X,D)$ be the group of divisors of
$\operatorname {Div}(X,D)$ be the group of divisors of ![]() $X$ supported on
$X$ supported on ![]() $D$ and denote by
$D$ and denote by ![]() $k$ a field of characteristic
$k$ a field of characteristic ![]() $0$. For every effective divisor
$0$. For every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$, we let
$r\geq 0$, we let ![]() $\operatorname {MIC}_r(X,D,R)$ be the category of flat bundles on
$\operatorname {MIC}_r(X,D,R)$ be the category of flat bundles on ![]() $U$ with rank smaller than
$U$ with rank smaller than ![]() $r$ and irregularity bounded by
$r$ and irregularity bounded by ![]() $R$ along
$R$ along ![]() $D$.
$D$.
Theorem 0.1 Let ![]() $X$ be a smooth projective surface over
$X$ be a smooth projective surface over ![]() $k$. Let
$k$. Let ![]() $D$ be a normal crossing divisor of
$D$ be a normal crossing divisor of ![]() $X$. Then, there exists a quadratic polynomial
$X$. Then, there exists a quadratic polynomial ![]() $C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor
$C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {E}$ of
$\mathcal {E}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
A second consequence of the existence of ![]() $\mathcal {M}_r(X,D,R)$ is the Lefschetz recognition principle. It relies on the heuristic principle that the formation of
$\mathcal {M}_r(X,D,R)$ is the Lefschetz recognition principle. It relies on the heuristic principle that the formation of ![]() $\mathcal {M}_r(X,D,R)$ should come packaged with functorialities. If
$\mathcal {M}_r(X,D,R)$ should come packaged with functorialities. If ![]() $f : Y\to X$ is a morphism of smooth projective varieties over
$f : Y\to X$ is a morphism of smooth projective varieties over ![]() $k$ such that
$k$ such that ![]() $f^*R$ makes sense and such that
$f^*R$ makes sense and such that ![]() $f^{-1}(D)$ is a normal crossing divisor, one expects the existence of a morphism of varieties
$f^{-1}(D)$ is a normal crossing divisor, one expects the existence of a morphism of varieties ![]() $\mathcal {M}_r(X,D,R)\to \mathcal {M}_r(Y,f^{-1}(D),f^*R)$ induced by the pull-back along
$\mathcal {M}_r(X,D,R)\to \mathcal {M}_r(Y,f^{-1}(D),f^*R)$ induced by the pull-back along ![]() $f: Y\to X$. Functorialities would make the study of
$f: Y\to X$. Functorialities would make the study of ![]() $\mathcal {M}_r(X,D,R)$ tractable through the curve case, where they should be much easier to construct since flat bundles on curves have no turning points. If
$\mathcal {M}_r(X,D,R)$ tractable through the curve case, where they should be much easier to construct since flat bundles on curves have no turning points. If ![]() $\mathcal {E}_0$ and
$\mathcal {E}_0$ and ![]() $\mathcal {E}_1$ are non-isomorphic flat bundles on
$\mathcal {E}_1$ are non-isomorphic flat bundles on ![]() $U$, one can find a hyperplane
$U$, one can find a hyperplane ![]() $H$ such that the restrictions of
$H$ such that the restrictions of ![]() $\mathcal {E}_0$ and
$\mathcal {E}_0$ and ![]() $\mathcal {E}_1$ to
$\mathcal {E}_1$ to ![]() $X\cap H$ are again non-isomorphic. When viewed as points of
$X\cap H$ are again non-isomorphic. When viewed as points of ![]() $\mathcal {M}_r(X,D,R)$, this means geometrically that
$\mathcal {M}_r(X,D,R)$, this means geometrically that ![]() $\mathcal {E}_0$ and
$\mathcal {E}_0$ and ![]() $\mathcal {E}_1$ do not lie in the same fibre of
$\mathcal {E}_1$ do not lie in the same fibre of ![]() $\mathcal {M}_r(X,D,R)\to \mathcal {M}_r(X\cap H,f_H^{-1}(D), f_H^*R)$ where
$\mathcal {M}_r(X,D,R)\to \mathcal {M}_r(X\cap H,f_H^{-1}(D), f_H^*R)$ where ![]() $f_H : X\cap H \to X$ is the inclusion. One thus expects the induced morphism of schemes
$f_H : X\cap H \to X$ is the inclusion. One thus expects the induced morphism of schemes
to be a closed immersion. Since ![]() $\mathcal {M}_r(X,D,R)$ should be of finite type, this implies the existence of hyperplanes
$\mathcal {M}_r(X,D,R)$ should be of finite type, this implies the existence of hyperplanes ![]() $H_1,\ldots, H_N$ depending only on
$H_1,\ldots, H_N$ depending only on ![]() $X,D,R$ and
$X,D,R$ and ![]() $r$ such that if we put
$r$ such that if we put ![]() $f: \bigsqcup X\cap H_i \to X$, then
$f: \bigsqcup X\cap H_i \to X$, then ![]() $\mathcal {M}_r(X,D,R)\to \mathcal {M}_r(Y,f^{-1}(D), f^*R)$ is a closed immersion. Put in the language of flat bundles, two objects of
$\mathcal {M}_r(X,D,R)\to \mathcal {M}_r(Y,f^{-1}(D), f^*R)$ is a closed immersion. Put in the language of flat bundles, two objects of ![]() $\operatorname {MIC}_r(X,D,R)$ are isomorphic if and only their pull-back to
$\operatorname {MIC}_r(X,D,R)$ are isomorphic if and only their pull-back to ![]() $\bigsqcup X\cap H_i$ are isomorphic. This is the Lefschetz recognition principle. We are led to introduce the following.
$\bigsqcup X\cap H_i$ are isomorphic. This is the Lefschetz recognition principle. We are led to introduce the following.
Definition 0.2 Let ![]() $X$ be a smooth projective variety of dimension
$X$ be a smooth projective variety of dimension ![]() $n\geq 2$ over a field
$n\geq 2$ over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $0$. Let
$0$. Let ![]() $D$ be a simple normal crossing divisor of
$D$ be a simple normal crossing divisor of ![]() $X$. Let
$X$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Let
$X\to \mathbb {P}$ be a closed immersion in some projective space. Let ![]() $\mathcal {C}$ be a class of flat vector bundles on
$\mathcal {C}$ be a class of flat vector bundles on ![]() $X-D$. Let
$X-D$. Let ![]() $\mathcal {H}$ be a set of hyperplanes in
$\mathcal {H}$ be a set of hyperplanes in ![]() $\mathbb {P}$ meeting
$\mathbb {P}$ meeting ![]() $X$ transversally. We say that
$X$ transversally. We say that ![]() $\mathcal {H}$ realizes the Lefschetz recognition principle for
$\mathcal {H}$ realizes the Lefschetz recognition principle for ![]() $\mathcal {C}$ if for every
$\mathcal {C}$ if for every ![]() $\mathcal {M}_1,\mathcal {M}_2 \in \mathcal {C}$, the flat bundles
$\mathcal {M}_1,\mathcal {M}_2 \in \mathcal {C}$, the flat bundles ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ are isomorphic if and only if
$\mathcal {M}_2$ are isomorphic if and only if ![]() $\mathcal {M}_1|_{X\cap H}$ and
$\mathcal {M}_1|_{X\cap H}$ and ![]() $\mathcal {M}_2|_{X\cap H}$ are isomorphic for every
$\mathcal {M}_2|_{X\cap H}$ are isomorphic for every ![]() $H\in \mathcal {H}$.
$H\in \mathcal {H}$.
Our second main result is a proof of the Lefschetz recognition principle for ![]() $\mathcal {C} = \operatorname {MIC}_r(X,D,R)$ in any dimension.
$\mathcal {C} = \operatorname {MIC}_r(X,D,R)$ in any dimension.
Theorem 0.3 Let ![]() $X$ be a smooth projective variety of dimension
$X$ be a smooth projective variety of dimension ![]() $n\geq 2$ over
$n\geq 2$ over ![]() $k$. Let
$k$. Let ![]() $D$ be a simple normal crossing divisor of
$D$ be a simple normal crossing divisor of ![]() $X$. Let
$X$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a polynomial
$X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree ![]() $4$ such that for every effective divisor
$4$ such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$, there is a dense open subset of
$r\geq 0$, there is a dense open subset of ![]() $\Omega (R,r) \subset (\mathbb {P}^{\vee })^{K(R,r)}$ such that every
$\Omega (R,r) \subset (\mathbb {P}^{\vee })^{K(R,r)}$ such that every ![]() $(H_1,\ldots, H_{K(R,r)})\in \Omega (R,r)$ realizes the Lefschetz recognition principle for
$(H_1,\ldots, H_{K(R,r)})\in \Omega (R,r)$ realizes the Lefschetz recognition principle for ![]() $\operatorname {MIC}_r(X,D,R)$.
$\operatorname {MIC}_r(X,D,R)$.
See Theorem 7.5 for explicit conditions defining the dense open set ![]() $\Omega (R,r)$.
$\Omega (R,r)$.
Although the statements of cohomological boundedness and the Lefschetz recognition principle were derived separately from the existence of ![]() $\mathcal {M}_r(X,D,R)$, it turns out that for surfaces, the latter is a consequence of the former. Let us explain how. Let
$\mathcal {M}_r(X,D,R)$, it turns out that for surfaces, the latter is a consequence of the former. Let us explain how. Let ![]() $j : U\to X$ be the open immersion and let
$j : U\to X$ be the open immersion and let ![]() $\mathcal {E}$ be a flat bundle on
$\mathcal {E}$ be a flat bundle on ![]() $U$. The
$U$. The ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $j_*\mathcal {E}$ is coherent and as such, a canonical
$j_*\mathcal {E}$ is coherent and as such, a canonical ![]() $\dim U$-cycle
$\dim U$-cycle ![]() $CC( j_*\mathcal {E})$ of the cotangent bundle
$CC( j_*\mathcal {E})$ of the cotangent bundle ![]() $T^*X$ was attached to it by Kashiwara and Schapira [Reference Kashiwara and SchapiraKS90]. This is the characteristic cycle of
$T^*X$ was attached to it by Kashiwara and Schapira [Reference Kashiwara and SchapiraKS90]. This is the characteristic cycle of ![]() $j_* \mathcal {E}$. The cycle
$j_* \mathcal {E}$. The cycle ![]() $CC( j_*\mathcal {E})$ tells how far the
$CC( j_*\mathcal {E})$ tells how far the ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $j_*\mathcal {E}$ is from being a flat connection on
$j_*\mathcal {E}$ is from being a flat connection on ![]() $X$ and thus provides a geometric measure of the complexity of the differential system underlying
$X$ and thus provides a geometric measure of the complexity of the differential system underlying ![]() $j_*\mathcal {E}$. The cycle
$j_*\mathcal {E}$. The cycle ![]() $CC( j_*\mathcal {E})$ is Lagrangian. If
$CC( j_*\mathcal {E})$ is Lagrangian. If ![]() $X$ is a surface,
$X$ is a surface, ![]() $CC( j_*\mathcal {E})$ is thus a combination of the zero section of
$CC( j_*\mathcal {E})$ is thus a combination of the zero section of ![]() $T^*X$, the conormal bundles of the components of
$T^*X$, the conormal bundles of the components of ![]() $D$ and the conormal bundles of some points of
$D$ and the conormal bundles of some points of ![]() $D$. If
$D$. If ![]() $\mathcal {E}'$ is another flat bundle on
$\mathcal {E}'$ is another flat bundle on ![]() $U$, then any smooth curve transverse to
$U$, then any smooth curve transverse to ![]() $D$ and avoiding the points whose conormal bundle contributes to
$D$ and avoiding the points whose conormal bundle contributes to ![]() $CC(j_*{\mathcal {H}}\! \operatorname {om}(\mathcal {E}_1,\mathcal {E}_2))$ where
$CC(j_*{\mathcal {H}}\! \operatorname {om}(\mathcal {E}_1,\mathcal {E}_2))$ where ![]() $\mathcal {E}_1,\mathcal {E}_2\in \{\mathcal {E},\mathcal {E}'\}$ distinguishes
$\mathcal {E}_1,\mathcal {E}_2\in \{\mathcal {E},\mathcal {E}'\}$ distinguishes ![]() $\mathcal {E}$ and
$\mathcal {E}$ and ![]() $\mathcal {E}'$ after restriction. See Corollary 7.4. This observation translates the statement of Theorem 0.3 into the problem of finding a universal bound for the number of points of
$\mathcal {E}'$ after restriction. See Corollary 7.4. This observation translates the statement of Theorem 0.3 into the problem of finding a universal bound for the number of points of ![]() $D$ whose conormal bundle contributes to
$D$ whose conormal bundle contributes to ![]() $CC( j_*\mathcal {E})$ for
$CC( j_*\mathcal {E})$ for ![]() $\mathcal {E}$ in
$\mathcal {E}$ in ![]() $\operatorname {MIC}_r(X,D,R)$. This question is cohomological since by Kashiwara and Dubson's formula [Reference DubsonDub84], every such point contributes to de Rham cohomology. This is how Theorem 0.3 follows from Theorem 0.1 for surfaces.
$\operatorname {MIC}_r(X,D,R)$. This question is cohomological since by Kashiwara and Dubson's formula [Reference DubsonDub84], every such point contributes to de Rham cohomology. This is how Theorem 0.3 follows from Theorem 0.1 for surfaces.
The main result of [Reference TeyssierTey23] implies that the points of the smooth locus of ![]() $D$ whose conormal bundle contributes to
$D$ whose conormal bundle contributes to ![]() $CC( j_*\mathcal {E})$ and
$CC( j_*\mathcal {E})$ and ![]() $CC( j_*{\mathcal {E}} \operatorname {nd}\mathcal {E})$ are exactly the turning points of
$CC( j_*{\mathcal {E}} \operatorname {nd}\mathcal {E})$ are exactly the turning points of ![]() $\mathcal {E}$ along
$\mathcal {E}$ along ![]() $D$. From the above discussion, cohomological boundedness thus yields a universal bound on the number of turning points of objects in
$D$. From the above discussion, cohomological boundedness thus yields a universal bound on the number of turning points of objects in ![]() $\operatorname {MIC}_r(X,D,R)$. We prove in any dimension a stronger universal bound (Theorem 6.9).
$\operatorname {MIC}_r(X,D,R)$. We prove in any dimension a stronger universal bound (Theorem 6.9).
Theorem 0.4 Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$. Let
$k$. Let ![]() $D$ be a normal crossing divisor of
$D$ be a normal crossing divisor of ![]() $X$. Let
$X$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a quadratic polynomial
$X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a quadratic polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {E}$ of
$\mathcal {E}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, the degree of the turning locus of
$\operatorname {MIC}_r(X,D,R)$, the degree of the turning locus of ![]() $\mathcal {E}$ along
$\mathcal {E}$ along ![]() $D$ is smaller than
$D$ is smaller than ![]() $K(R,r)$.
$K(R,r)$.
For a flat bundle ![]() $\mathcal {E}$, Kedlaya [Reference KedlayaKed11] and Mochizuki [Reference MochizukiMoc11] proved that the turning locus of
$\mathcal {E}$, Kedlaya [Reference KedlayaKed11] and Mochizuki [Reference MochizukiMoc11] proved that the turning locus of ![]() $\mathcal {E}$ along
$\mathcal {E}$ along ![]() $D$ can be eliminated by enough blow-up. Theorem 0.4 is thus consistent with Esnault and Langer's expectation that there should exist a universal bound on the number of blow-up needed to achieve good formal decomposition for objects in
$D$ can be eliminated by enough blow-up. Theorem 0.4 is thus consistent with Esnault and Langer's expectation that there should exist a universal bound on the number of blow-up needed to achieve good formal decomposition for objects in ![]() $\operatorname {MIC}_r(X,D,R)$. Their insight is that controlling the number of blow-ups should give the required bound on the Chern classes of Deligne–Malgrange lattices to construct the moduli
$\operatorname {MIC}_r(X,D,R)$. Their insight is that controlling the number of blow-ups should give the required bound on the Chern classes of Deligne–Malgrange lattices to construct the moduli ![]() $\mathcal {M}_r(X,D,R)$. By purity of turning loci proved by André for
$\mathcal {M}_r(X,D,R)$. By purity of turning loci proved by André for ![]() $D$ smooth [Reference AndréAnd07] and by Kedlaya in general [Reference KedlayaKed21], we deduce the following (Theorem 6.10).
$D$ smooth [Reference AndréAnd07] and by Kedlaya in general [Reference KedlayaKed21], we deduce the following (Theorem 6.10).
Theorem 0.5 Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $k$. Let
$k$. Let ![]() $D$ be a normal crossing divisor of
$D$ be a normal crossing divisor of ![]() $X$. Let
$X$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a quadratic polynomial
$X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a quadratic polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {E}$ of
$\mathcal {E}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, the set of irreducible components of the turning locus of
$\operatorname {MIC}_r(X,D,R)$, the set of irreducible components of the turning locus of ![]() $\mathcal {E}$ along
$\mathcal {E}$ along ![]() $D$ is smaller than
$D$ is smaller than ![]() $K(R,r)$.
$K(R,r)$.
We summarize the interplay (at least for surfaces) of the above results and heuristic in the following diagram, to be understood with bounded rank and irregularity.

We finally introduce the main tool of this paper and describe an extra application. Let ![]() $X$ be a smooth connected variety over
$X$ be a smooth connected variety over ![]() $k$. Let
$k$. Let ![]() $D$ be a normal crossing divisor of
$D$ be a normal crossing divisor of ![]() $X$. Let
$X$. Let ![]() $\mathcal {E}$ be a flat bundle on
$\mathcal {E}$ be a flat bundle on ![]() $j :U:=X\setminus D\to X$. For every proper birational morphism
$j :U:=X\setminus D\to X$. For every proper birational morphism ![]() $p : Y\to X$ where
$p : Y\to X$ where ![]() $Y$ is smooth and
$Y$ is smooth and ![]() $E:=p^{-1}(D)$ is a normal crossing divisor, Kedlaya attached to
$E:=p^{-1}(D)$ is a normal crossing divisor, Kedlaya attached to ![]() $\mathcal {E}$ an effective divisor
$\mathcal {E}$ an effective divisor ![]() $\operatorname {Irr}(Y,p^+\mathcal {E})$ supported on
$\operatorname {Irr}(Y,p^+\mathcal {E})$ supported on ![]() $E$ whose coefficient along a component
$E$ whose coefficient along a component ![]() $Z$ is the generic irregularity number of
$Z$ is the generic irregularity number of ![]() $\mathcal {E}$ along
$\mathcal {E}$ along ![]() $Z$ or, equivalently, the coefficient of
$Z$ or, equivalently, the coefficient of ![]() $T^*_ZY$ in
$T^*_ZY$ in ![]() $CC(\jmath _{*}\mathcal {E})$, where
$CC(\jmath _{*}\mathcal {E})$, where ![]() $\jmath : U\to Y$ is the inclusion. This collection of divisors organizes into an element
$\jmath : U\to Y$ is the inclusion. This collection of divisors organizes into an element ![]() $\operatorname {Irr} \mathcal {E}$ of the group
$\operatorname {Irr} \mathcal {E}$ of the group ![]() $\textbf {Div}(X):=\varprojlim _{Y\rightarrow X} \operatorname {Div}(Y)$ of
$\textbf {Div}(X):=\varprojlim _{Y\rightarrow X} \operatorname {Div}(Y)$ of ![]() $b$-divisors, where
$b$-divisors, where ![]() $p : Y\to X$ runs over the poset of morphisms as above and where the transition maps are push-forward. In particular, an element of
$p : Y\to X$ runs over the poset of morphisms as above and where the transition maps are push-forward. In particular, an element of ![]() $\textbf {Div}(X)$ is a
$\textbf {Div}(X)$ is a ![]() $\mathbb {Z}$-valued function on the set of divisorial valuations on
$\mathbb {Z}$-valued function on the set of divisorial valuations on ![]() $X$. The
$X$. The ![]() $b$-divisor
$b$-divisor ![]() $\operatorname {Irr}\mathcal {E}$ is the irregularity
$\operatorname {Irr}\mathcal {E}$ is the irregularity ![]() $b$-divisor of
$b$-divisor of ![]() $\mathcal{E}$ along
$\mathcal{E}$ along ![]() $D$. In the group
$D$. In the group ![]() $\textbf {Div}(X)$ lies the subgroup of Cartier
$\textbf {Div}(X)$ lies the subgroup of Cartier ![]() $b$-divisor defined as
$b$-divisor defined as ![]() $\varinjlim _{Y\rightarrow X}\operatorname {Div}(Y)$ where the transition maps are pull-backs. Fundamental to this paper is Kedlaya's theorem [Reference KedlayaKed21] that
$\varinjlim _{Y\rightarrow X}\operatorname {Div}(Y)$ where the transition maps are pull-backs. Fundamental to this paper is Kedlaya's theorem [Reference KedlayaKed21] that ![]() $\operatorname {Irr}\mathcal {E}$ is a nef Cartier
$\operatorname {Irr}\mathcal {E}$ is a nef Cartier ![]() $b$-divisor with the property that
$b$-divisor with the property that ![]() $\operatorname {Irr}\mathcal {E}$ and
$\operatorname {Irr}\mathcal {E}$ and ![]() $\operatorname {Irr}{\mathcal {E}}\!\operatorname{nd}\mathcal {E}$ lie in the subgroup
$\operatorname {Irr}{\mathcal {E}}\!\operatorname{nd}\mathcal {E}$ lie in the subgroup ![]() $\operatorname {Div}(X)$ of
$\operatorname {Div}(X)$ of ![]() $\textbf {Div}(X)$ if and only if
$\textbf {Div}(X)$ if and only if ![]() $\mathcal {E}$ has good formal decomposition along
$\mathcal {E}$ has good formal decomposition along ![]() $D$. We show in § 5.3 that
$D$. We show in § 5.3 that ![]() $\operatorname {Irr}\mathcal {E}$ and
$\operatorname {Irr}\mathcal {E}$ and ![]() $\operatorname {rk} \mathcal {E}$ determine
$\operatorname {rk} \mathcal {E}$ determine ![]() $CC(j_*\mathcal {E})$, and it is an intriguing question to understand how
$CC(j_*\mathcal {E})$, and it is an intriguing question to understand how ![]() $CC(j_*\mathcal {E})$ relates to
$CC(j_*\mathcal {E})$ relates to ![]() $\operatorname {Irr}\mathcal {E}$. If
$\operatorname {Irr}\mathcal {E}$. If ![]() $X$ is a surface, we answer this question using a new operation on
$X$ is a surface, we answer this question using a new operation on ![]() $b$-divisors, the partial discrepancy
$b$-divisors, the partial discrepancy ![]() $\delta : \textbf {Div}(X)\to \textbf {Div}(X)$. The partial discrepancy measures the failure of a
$\delta : \textbf {Div}(X)\to \textbf {Div}(X)$. The partial discrepancy measures the failure of a ![]() $b$-divisor
$b$-divisor ![]() $Z$ to lie in the image of
$Z$ to lie in the image of ![]() $\operatorname {Div}(X)\to \textbf {Div}(X)$ in the sense that if it does, then
$\operatorname {Div}(X)\to \textbf {Div}(X)$ in the sense that if it does, then ![]() $\delta Z=0$. We prove that if
$\delta Z=0$. We prove that if ![]() $Z$ is a nef Cartier
$Z$ is a nef Cartier ![]() $b$-divisor, then
$b$-divisor, then ![]() $\delta Z$ is an effective
$\delta Z$ is an effective ![]() $b$-divisor with finite support when viewed as a function on the set of divisorial valuations on
$b$-divisor with finite support when viewed as a function on the set of divisorial valuations on ![]() $X$. Hence, the sum of its values, denoted by
$X$. Hence, the sum of its values, denoted by ![]() $\int _X \delta Z$ is a well-defined positive integer. For a subset
$\int _X \delta Z$ is a well-defined positive integer. For a subset ![]() $A$ of
$A$ of ![]() $X$, we denote by
$X$, we denote by ![]() $\int _A \delta Z$ the sum of the values of
$\int _A \delta Z$ the sum of the values of ![]() $\delta Z$ over the set of divisorial valuations whose centres on
$\delta Z$ over the set of divisorial valuations whose centres on ![]() $X$ lie in
$X$ lie in ![]() $A$. Using the partial discrepancy, we prove the following formula for the characteristic cycle of flat bundles on surfaces (Theorem 5.18).
$A$. Using the partial discrepancy, we prove the following formula for the characteristic cycle of flat bundles on surfaces (Theorem 5.18).
Theorem 0.6 Let ![]() $X$ be a smooth projective surface over an algebraically closed field of characteristic
$X$ be a smooth projective surface over an algebraically closed field of characteristic ![]() $0$. Let
$0$. Let ![]() $D$ be a normal crossing divisor of
$D$ be a normal crossing divisor of ![]() $X$. Let
$X$. Let ![]() $\mathcal {E}$ be a flat bundle on
$\mathcal {E}$ be a flat bundle on ![]() $j :U:=X\setminus D\to X$. Then
$j :U:=X\setminus D\to X$. Then
 \[ CC(j_*\mathcal{E}) = \operatorname{rk} \mathcal{E} \cdot CC(\mathcal{O}_{X}(\ast D)) + LC(\operatorname{Irr}(X,\mathcal{E})) + \sum_{P\in D} \bigg( \int_{P} \delta\operatorname{Irr}\mathcal{E}\bigg) \cdot T_{P}^*X. \]
\[ CC(j_*\mathcal{E}) = \operatorname{rk} \mathcal{E} \cdot CC(\mathcal{O}_{X}(\ast D)) + LC(\operatorname{Irr}(X,\mathcal{E})) + \sum_{P\in D} \bigg( \int_{P} \delta\operatorname{Irr}\mathcal{E}\bigg) \cdot T_{P}^*X. \]
In the above formula, ![]() $LC(\operatorname {Irr}(X,\mathcal {E}))$ is a Lagrangian cycle depending only on the divisor
$LC(\operatorname {Irr}(X,\mathcal {E}))$ is a Lagrangian cycle depending only on the divisor ![]() $\operatorname {Irr}(X,\mathcal {E})$ supported on
$\operatorname {Irr}(X,\mathcal {E})$ supported on ![]() $D$ attached to
$D$ attached to ![]() $\mathcal {E}$. In particular, it depends on
$\mathcal {E}$. In particular, it depends on ![]() $\mathcal {E}$ only via generic data along the components of
$\mathcal {E}$ only via generic data along the components of ![]() $D$. A nice feature of the above formula is to make explicit the means by which the lack of good formal decomposition reflects in the characteristic cycle. By definition of the partial discrepancy, it shows, in particular, that the characteristic cycle is only sensitive to the turning points lying in the smooth locus of the successive inverse images of
$D$. A nice feature of the above formula is to make explicit the means by which the lack of good formal decomposition reflects in the characteristic cycle. By definition of the partial discrepancy, it shows, in particular, that the characteristic cycle is only sensitive to the turning points lying in the smooth locus of the successive inverse images of ![]() $D$ by the successive blow-up needed to achieve good formal decomposition. From the Kashiwara and Dubson formula [Reference DubsonDub84], we deduce the following Grothendieck–Ogg Shafarevich-type formula for flat bundles on surfaces (Theorem 5.20).
$D$ by the successive blow-up needed to achieve good formal decomposition. From the Kashiwara and Dubson formula [Reference DubsonDub84], we deduce the following Grothendieck–Ogg Shafarevich-type formula for flat bundles on surfaces (Theorem 5.20).
Theorem 0.7 Let ![]() $X$ be a smooth projective surface over
$X$ be a smooth projective surface over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $D$ be a normal crossing divisor of
$D$ be a normal crossing divisor of ![]() $X$. Let
$X$. Let ![]() $\mathcal {E}$ be a flat bundle on
$\mathcal {E}$ be a flat bundle on ![]() $j :U:=X\setminus D\to X$. Then
$j :U:=X\setminus D\to X$. Then
We now give a linear overview of the paper. Section 1 gathers some general material on ![]() $\mathcal {D}$-modules as well as Kedlaya's results on irregularity
$\mathcal {D}$-modules as well as Kedlaya's results on irregularity ![]() $b$-divisors. Section 2 introduces the cohomological boundedness conjecture for flat bundles with bounded rank and irregularity at infinity. The main upshot of § 2 is Corollary 2.17 stating that cohomological boundedness is equivalent to an a priori weaker conjecture, the
$b$-divisors. Section 2 introduces the cohomological boundedness conjecture for flat bundles with bounded rank and irregularity at infinity. The main upshot of § 2 is Corollary 2.17 stating that cohomological boundedness is equivalent to an a priori weaker conjecture, the ![]() $\chi$-boundedness conjecture asking for a universal bound on the global Euler–Poincaré characteristic of the de Rham cohomology. Section 3 is the main technical core of this paper. In a relative situation, it provides a mechanism for deducing
$\chi$-boundedness conjecture asking for a universal bound on the global Euler–Poincaré characteristic of the de Rham cohomology. Section 3 is the main technical core of this paper. In a relative situation, it provides a mechanism for deducing ![]() $\chi$-boundedness out of
$\chi$-boundedness out of ![]() $\chi$-boundedness for the generic fibre provided the turning locus is contained in a fibre. See Proposition 3.23. Section 4 is devoted to the construction of the partial discrepancy
$\chi$-boundedness for the generic fibre provided the turning locus is contained in a fibre. See Proposition 3.23. Section 4 is devoted to the construction of the partial discrepancy ![]() $b$-divisor attached to a
$b$-divisor attached to a ![]() $b$-divisor on a smooth surface. Its upshot is Proposition 4.15 ensuring that the partial discrepancy of a nef Cartier
$b$-divisor on a smooth surface. Its upshot is Proposition 4.15 ensuring that the partial discrepancy of a nef Cartier ![]() $b$-divisor is a
$b$-divisor is a ![]() $b$-divisor with finite support when viewed as a function on the set of divisorial valuations. Section 5 is an application of § 4 to the proof of Theorems 0.6 and 0.7. Section 6 gives the proof of cohomological boundedness for surfaces. Section 7 provides the proof of the Lefschetz recognition principle. In § 8, the techniques of this paper are used to obtain a Lefschetz theorem for the differential Galois group of flat bundles under some uncountability assumption of the base field.
$b$-divisor with finite support when viewed as a function on the set of divisorial valuations. Section 5 is an application of § 4 to the proof of Theorems 0.6 and 0.7. Section 6 gives the proof of cohomological boundedness for surfaces. Section 7 provides the proof of the Lefschetz recognition principle. In § 8, the techniques of this paper are used to obtain a Lefschetz theorem for the differential Galois group of flat bundles under some uncountability assumption of the base field.
1. Geometric and  $\mathcal {D}$-module preparations
$\mathcal {D}$-module preparations
1.1 Base field
In this paper, ![]() $k$ will denote a field of characteristic
$k$ will denote a field of characteristic ![]() $0$. If
$0$. If ![]() $X$ is a variety over
$X$ is a variety over ![]() $k$, we denote by
$k$, we denote by ![]() $X^{\operatorname {sm}}$ the smooth locus of
$X^{\operatorname {sm}}$ the smooth locus of ![]() $X$ and by
$X$ and by ![]() $X^{\operatorname {sing}}$ the singular locus of
$X^{\operatorname {sing}}$ the singular locus of ![]() $X$. If
$X$. If ![]() $k\subset K$ is a field extension, we denote by
$k\subset K$ is a field extension, we denote by ![]() $X_K$ the pull-back of
$X_K$ the pull-back of ![]() $X$ over
$X$ over ![]() $K$.
$K$.
1.2 Pair of varieties
A pair over ![]() $k$ is the data
$k$ is the data ![]() $(X,D)$ of a smooth variety
$(X,D)$ of a smooth variety ![]() $X$ over
$X$ over ![]() $k$ with a reduced divisor
$k$ with a reduced divisor ![]() $D$. An analytic pair is the data
$D$. An analytic pair is the data ![]() $(X,D)$ of a complex manifold
$(X,D)$ of a complex manifold ![]() $X$ with a reduced divisor
$X$ with a reduced divisor ![]() $D$. In both situations, we denote by
$D$. In both situations, we denote by ![]() $\operatorname {Div}(X,D)$ the group of divisors of
$\operatorname {Div}(X,D)$ the group of divisors of ![]() $X$ supported on
$X$ supported on ![]() $D$, that is,
$D$, that is, ![]() $\operatorname {Div}(X,D)$ is the free abelian group over the set of irreducible components of
$\operatorname {Div}(X,D)$ is the free abelian group over the set of irreducible components of ![]() $D$. We denote by
$D$. We denote by ![]() $\operatorname {fdeg} : \operatorname {Div}(X,D)\to \mathbb {Z}$ the formal degree function, that is the group morphism sending each irreducible component of
$\operatorname {fdeg} : \operatorname {Div}(X,D)\to \mathbb {Z}$ the formal degree function, that is the group morphism sending each irreducible component of ![]() $D$ to
$D$ to ![]() $1$. Note that if
$1$. Note that if ![]() $k\subset K$ is a field extension, then
$k\subset K$ is a field extension, then ![]() $\operatorname {fdeg} R\leq \operatorname {fdeg} R_K$, where
$\operatorname {fdeg} R\leq \operatorname {fdeg} R_K$, where ![]() $R_K$ denotes the pull-back of
$R_K$ denotes the pull-back of ![]() $R$ to
$R$ to ![]() $X_K$.
$X_K$.
If ![]() $P$ is a property of algebraic or analytic varieties, a
$P$ is a property of algebraic or analytic varieties, a ![]() $P$-pair
$P$-pair ![]() $(X,D)$ will refer to a pair
$(X,D)$ will refer to a pair ![]() $(X,D)$ such that
$(X,D)$ such that ![]() $X$ satisfies
$X$ satisfies ![]() $P$. Finally, a
$P$. Finally, a ![]() $P$-normal crossing pair
$P$-normal crossing pair ![]() $(X,D)$ is a
$(X,D)$ is a ![]() $P$-pair such that
$P$-pair such that ![]() $D$ has normal crossing.
$D$ has normal crossing.
A morphism of pairs ![]() $f: (Y,E)\to (X,D)$ over
$f: (Y,E)\to (X,D)$ over ![]() $k$ is a morphism
$k$ is a morphism ![]() $f : X\to Y$ of algebraic varieties over
$f : X\to Y$ of algebraic varieties over ![]() $k$ such that
$k$ such that ![]() $f^{-1}(D)=E$.
$f^{-1}(D)=E$.
1.3 Transversality
We recall the transversality conditions from [Reference BeilinsonBei16].
Definition 1.1 Let ![]() $f:Y\to X$ be a morphism between smooth varieties over
$f:Y\to X$ be a morphism between smooth varieties over ![]() $k$. Let
$k$. Let ![]() $C$ be a closed conical subset of
$C$ be a closed conical subset of ![]() $T^*X$. Let
$T^*X$. Let ![]() $\overline y$ be a geometric point above a point
$\overline y$ be a geometric point above a point ![]() $y$ of
$y$ of ![]() $Y$. We say that
$Y$. We say that ![]() $f:Y\to X$ is
$f:Y\to X$ is ![]() $C$-transversal at
$C$-transversal at ![]() $y$ if
$y$ if
where ![]() $df_{\overline y}: T^*_{f(\overline y)}X \to T^*_{\overline y}Y$ is the cotangent map of
$df_{\overline y}: T^*_{f(\overline y)}X \to T^*_{\overline y}Y$ is the cotangent map of ![]() $f$ at
$f$ at ![]() $\overline y$. We say that
$\overline y$. We say that ![]() $f:Y\to X$ is
$f:Y\to X$ is ![]() $C$-transversal if it is
$C$-transversal if it is ![]() $C$-transversal at every point of
$C$-transversal at every point of ![]() $Y$.
$Y$.
If ![]() $f:Y\to X$ is
$f:Y\to X$ is ![]() $C$-transversal, let
$C$-transversal, let ![]() $f^\circ C$ be the scheme-theoretic image of
$f^\circ C$ be the scheme-theoretic image of ![]() $Y\times _XC$ in
$Y\times _XC$ in ![]() $T^*Y$ by the canonical map
$T^*Y$ by the canonical map ![]() $df: Y\times _XT^*X\to T^*Y$. As proved in [Reference BeilinsonBei16, Lemma 1.2], the map
$df: Y\times _XT^*X\to T^*Y$. As proved in [Reference BeilinsonBei16, Lemma 1.2], the map ![]() $df:Y\times _XC\to f^\circ C$ is finite and
$df:Y\times _XC\to f^\circ C$ is finite and ![]() $f^\circ C$ is a closed conical subset of
$f^\circ C$ is a closed conical subset of ![]() $T^*Y$.
$T^*Y$.
In the next transversality criterion, we use an extra operation on closed conical subsets of cotangent bundles. Let ![]() $f:X\to Y$ be a proper morphism between smooth varieties over
$f:X\to Y$ be a proper morphism between smooth varieties over ![]() $k$. Let
$k$. Let ![]() $C$ be a closed conical subset of
$C$ be a closed conical subset of ![]() $T^*X$. We denote by
$T^*X$. We denote by ![]() $f_{\circ }C$ the closed conical subset of
$f_{\circ }C$ the closed conical subset of ![]() $T^*Y$ defined as the image of
$T^*Y$ defined as the image of ![]() $df^{-1}(C)\subset X \times _Y T^*Y$ by the projection
$df^{-1}(C)\subset X \times _Y T^*Y$ by the projection ![]() $X \times _Y T^*Y\to T^*Y$, where
$X \times _Y T^*Y\to T^*Y$, where ![]() $df : X\times _Y T^*Y\to T^*X$ is the canonical map.
$df : X\times _Y T^*Y\to T^*X$ is the canonical map.
Lemma 1.2 Let

be a cartesian diagram of smooth varieties over ![]() $k$ whose arrows are closed immersions. Let
$k$ whose arrows are closed immersions. Let ![]() $C$ be a closed conical subset of
$C$ be a closed conical subset of ![]() $T^*X$. Let
$T^*X$. Let ![]() $x\in Y$ and let us abuse notation by viewing
$x\in Y$ and let us abuse notation by viewing ![]() $x$ as a point in
$x$ as a point in ![]() $X$,
$X$, ![]() $H$ and
$H$ and ![]() $P$. Then, the following statements hold.
$P$. Then, the following statements hold.
(i) If
 $g$ is
$g$ is  $i_{\circ }C$-transversal at
$i_{\circ }C$-transversal at  $x$, then
$x$, then  $f$ is
$f$ is  $C$-transversal at
$C$-transversal at  $x$.
$x$.(ii) Assume that
 $X$ and
$X$ and  $H$ are transverse at
$H$ are transverse at  $x$. If
$x$. If  $f$ is
$f$ is  $C$-transversal at
$C$-transversal at  $x$, then
$x$, then  $g$ is
$g$ is  $i_{\circ }C$-transversal at
$i_{\circ }C$-transversal at  $x$.
$x$.
Proof. Assume that ![]() $f$ is not
$f$ is not ![]() $C$-transversal at
$C$-transversal at ![]() $x$. This means that there exists a non-zero form
$x$. This means that there exists a non-zero form ![]() $\omega$ in
$\omega$ in ![]() $C_x$ vanishing on
$C_x$ vanishing on ![]() $T_xY \subset T_xX$. Since (1.3) is cartesian, so is the following induced diagram.
$T_xY \subset T_xX$. Since (1.3) is cartesian, so is the following induced diagram.

Via the choice of a supplementary for ![]() $T_x Y$ in
$T_x Y$ in ![]() $T_xH$ and a supplementary for
$T_xH$ and a supplementary for ![]() $T_xX + T_xH$ in
$T_xX + T_xH$ in ![]() $T_xP$, we can extend
$T_xP$, we can extend ![]() $\omega$ to a non-zero form
$\omega$ to a non-zero form ![]() $\eta$ on
$\eta$ on ![]() $T_xP$ vanishing on
$T_xP$ vanishing on ![]() $T_xH$. In particular,
$T_xH$. In particular, ![]() $\eta$ lies in
$\eta$ lies in ![]() $i_\circ C$ and
$i_\circ C$ and ![]() $g$ is not
$g$ is not ![]() $i_\circ C$-transversal at
$i_\circ C$-transversal at ![]() $x$ and part (i) is proven.
$x$ and part (i) is proven.
We now prove part (ii). Assume that ![]() $T_xX$ and
$T_xX$ and ![]() $T_x H$ generate
$T_x H$ generate ![]() $T_xP$ and that
$T_xP$ and that ![]() $f$ is
$f$ is ![]() $C$-transversal at
$C$-transversal at ![]() $x$. We argue by contradiction. Let
$x$. We argue by contradiction. Let ![]() $\eta$ be a non-zero form of
$\eta$ be a non-zero form of ![]() $i_\circ C$ above
$i_\circ C$ above ![]() $x$ such that
$x$ such that ![]() $\eta$ vanishes on
$\eta$ vanishes on ![]() $T_x H$. If
$T_x H$. If ![]() $i^*\eta =0$, the fact that
$i^*\eta =0$, the fact that ![]() $T_xX$ and
$T_xX$ and ![]() $T_x H$ generate
$T_x H$ generate ![]() $T_xP$ yields
$T_xP$ yields ![]() $\eta =0$, which is not possible. Thus,
$\eta =0$, which is not possible. Thus, ![]() $i^*\eta$ is a non-zero form of
$i^*\eta$ is a non-zero form of ![]() $C$ above
$C$ above ![]() $x$. By the transversality assumption,
$x$. By the transversality assumption, ![]() $i^*\eta$ does not vanish on
$i^*\eta$ does not vanish on ![]() $T_xY$, so
$T_xY$, so ![]() $\eta$ does not vanish on
$\eta$ does not vanish on ![]() $T_x H$. Contradiction. This concludes the proof of Lemma 1.2.
$T_x H$. Contradiction. This concludes the proof of Lemma 1.2.
We gather in Lemma 1.4 standard facts on transversality. See [Reference BeilinsonBei16, 1.2,2.2] and [Reference SaitoSai17, 3.4].
Lemma 1.4 Let ![]() $f : Y \to X$ be a morphism of smooth varieties over
$f : Y \to X$ be a morphism of smooth varieties over ![]() $k$. Let
$k$. Let ![]() $C,C' \subset T^*X$ be closed conical subsets. Let
$C,C' \subset T^*X$ be closed conical subsets. Let ![]() $x\in X$. Then the following hold.
$x\in X$. Then the following hold.
(i) Assume
 $C_x\subset C'_x$. If
$C_x\subset C'_x$. If  $f$ is
$f$ is  $C'$-transversal at
$C'$-transversal at  $x$, then
$x$, then  $f$ is
$f$ is  $C$-transversal at
$C$-transversal at  $x$.
$x$.(ii) If
 $f$ is
$f$ is  $C'$-transversal at
$C'$-transversal at  $x$ and
$x$ and  $C$-transversal at
$C$-transversal at  $x$, then
$x$, then  $f$ is
$f$ is  $C\cup C'$-transversal at
$C\cup C'$-transversal at  $x$.
$x$.(iii) Let
 $g : Z \to Y$ be a morphism of smooth varieties over
$g : Z \to Y$ be a morphism of smooth varieties over  $k$. The following conditions are equivalent:
$k$. The following conditions are equivalent:
(a)
 $f$ is
$f$ is  $C$-transversal on a neighbourhood of
$C$-transversal on a neighbourhood of  $g(Z)$ and
$g(Z)$ and  $g$ is
$g$ is  $f^{\circ }(C)$-transversal;
$f^{\circ }(C)$-transversal;(b)
 $f\circ g$ is
$f\circ g$ is  $C$-transversal.
$C$-transversal.
(iv) If
 $C'' \subset T^*Y$ is a closed conical subset, the set of points
$C'' \subset T^*Y$ is a closed conical subset, the set of points  $y\in Y$ at which
$y\in Y$ at which  $f$ is
$f$ is  $C''$-transversal is open in
$C''$-transversal is open in  $Y$.
$Y$.
1.4 Universal hyperplane
Let ![]() $E$ be a finite-dimensional vector space over
$E$ be a finite-dimensional vector space over ![]() $k$. Let
$k$. Let ![]() $E^{\ast }$ be its dual. Let
$E^{\ast }$ be its dual. Let ![]() $\mathbb {P}=\mathrm {Proj}(\operatorname {Sym} E^{\ast })$ and
$\mathbb {P}=\mathrm {Proj}(\operatorname {Sym} E^{\ast })$ and ![]() $\mathbb {P}^{\vee }=\mathrm {Proj}(\operatorname {Sym} E)$ be the associated projective spaces. The closed subscheme of
$\mathbb {P}^{\vee }=\mathrm {Proj}(\operatorname {Sym} E)$ be the associated projective spaces. The closed subscheme of ![]() $\mathbb {P}\times _k\mathbb {P}^{\vee }$ defined by
$\mathbb {P}\times _k\mathbb {P}^{\vee }$ defined by
is the universal family of hyperplanes of ![]() $\mathbb {P}$. Let
$\mathbb {P}$. Let ![]() $(X,D)$ be a quasi-projective normal crossing pair over
$(X,D)$ be a quasi-projective normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $i:X\to \mathbb P$ be an immersion. Put
$i:X\to \mathbb P$ be an immersion. Put ![]() $X_Q=X\times _{\mathbb {P}}Q$. Denote by
$X_Q=X\times _{\mathbb {P}}Q$. Denote by ![]() $p^{\vee }_X:X_Q\to \mathbb {P}^{\vee }$ the composition of
$p^{\vee }_X:X_Q\to \mathbb {P}^{\vee }$ the composition of ![]() $X_Q\to Q$ with the canonical projection
$X_Q\to Q$ with the canonical projection ![]() $p^{\vee }:Q\to \mathbb {P}^{\vee }$. Then, Bertini's theorem ensures the existence of a dense open subset
$p^{\vee }:Q\to \mathbb {P}^{\vee }$. Then, Bertini's theorem ensures the existence of a dense open subset ![]() $V\subset \mathbb {P}^{\vee }$ of hyperplanes
$V\subset \mathbb {P}^{\vee }$ of hyperplanes ![]() $H$ transverse to
$H$ transverse to ![]() $X$ such that
$X$ such that ![]() $D\cap H$ has normal crossings. In particular, if
$D\cap H$ has normal crossings. In particular, if ![]() $\eta$ denotes the generic point of
$\eta$ denotes the generic point of ![]() $\mathbb {P}^{\vee }$, we have the following commutative diagram with cartesian squares:
$\mathbb {P}^{\vee }$, we have the following commutative diagram with cartesian squares:

where ![]() $(X_\eta,D_\eta )$ is a quasi-projective pair over
$(X_\eta,D_\eta )$ is a quasi-projective pair over ![]() $\eta$ of dimension
$\eta$ of dimension ![]() $\dim X-1$ and where
$\dim X-1$ and where ![]() $D_\eta$ has normal crossings. The pair
$D_\eta$ has normal crossings. The pair ![]() $(X_\eta,D_\eta )$ is the generic hyperplane section of
$(X_\eta,D_\eta )$ is the generic hyperplane section of ![]() $(X,D)$.
$(X,D)$.
The following lemma provides a slight generalization of [Reference SaitoSai21, 1.3.7 (2)].
Lemma 1.5 Let ![]() $\mathbb {P}$ be a projective space over
$\mathbb {P}$ be a projective space over ![]() $k$. Let
$k$. Let ![]() $X$ be a smooth subvariety of
$X$ be a smooth subvariety of ![]() $\mathbb {P}$. Let
$\mathbb {P}$. Let ![]() $C\subset T^*X$ be a closed conical subset of pure dimension
$C\subset T^*X$ be a closed conical subset of pure dimension ![]() $\dim X$. Then there exists a dense open subset of hyperplanes
$\dim X$. Then there exists a dense open subset of hyperplanes ![]() $H$ transverse to
$H$ transverse to ![]() $X$ such that
$X$ such that ![]() $X\cap H \to X$ is
$X\cap H \to X$ is ![]() $C$-transversal.
$C$-transversal.
Proof. By Bertini's theorem, there exists a dense open subset ![]() $V_1\subset \mathbb {P}^{\vee }$ of hyperplanes transverse to
$V_1\subset \mathbb {P}^{\vee }$ of hyperplanes transverse to ![]() $X$. Observe that
$X$. Observe that ![]() $i_\circ C$ has pure dimension
$i_\circ C$ has pure dimension ![]() $\dim \mathbb {P}$. Thus, [Reference SaitoSai21, 1.3.7 (2)] ensures that there exists a dense open subset
$\dim \mathbb {P}$. Thus, [Reference SaitoSai21, 1.3.7 (2)] ensures that there exists a dense open subset ![]() $V_2 \subset \mathbb {P}^{\vee }$ of hyperplanes
$V_2 \subset \mathbb {P}^{\vee }$ of hyperplanes ![]() $H$ such that
$H$ such that ![]() $H\to \mathbb {P}$ is
$H\to \mathbb {P}$ is ![]() $i_\circ C$-transversal. From Lemma 1.2(i),
$i_\circ C$-transversal. From Lemma 1.2(i), ![]() $V_1\cap V_2$ thus meets our requirements.
$V_1\cap V_2$ thus meets our requirements.
1.5 Characteristic cycle for coherent  $\mathcal {D}$-modules
$\mathcal {D}$-modules
Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $0$. Let
$0$. Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$. We endow
$k$. We endow ![]() $\mathcal {D}_X$ with its filtration
$\mathcal {D}_X$ with its filtration ![]() $F$ by the order of differential operators. In particular, there is a canonical isomorphism
$F$ by the order of differential operators. In particular, there is a canonical isomorphism ![]() $\operatorname {gr}^F \mathcal {D}_X\simeq \pi _*\mathcal {O}_{T^*X}$ where
$\operatorname {gr}^F \mathcal {D}_X\simeq \pi _*\mathcal {O}_{T^*X}$ where ![]() $\pi : T^*X \to X$ is the canonical projection. Every coherent
$\pi : T^*X \to X$ is the canonical projection. Every coherent ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $\mathcal {M}$ admits a filtration
$\mathcal {M}$ admits a filtration ![]() $F_{\mathcal {M}}$ compatible with
$F_{\mathcal {M}}$ compatible with ![]() $F$ such that
$F$ such that ![]() $\operatorname {gr}^{F_{\mathcal {M}}}\mathcal {M}$ is a coherent
$\operatorname {gr}^{F_{\mathcal {M}}}\mathcal {M}$ is a coherent ![]() $\pi _*\mathcal {O}_{T^*X}$-module. Then,
$\pi _*\mathcal {O}_{T^*X}$-module. Then,
is a coherent ![]() $\mathcal {O}_{T^*X}$-module. Its characteristic cycle is a cycle of
$\mathcal {O}_{T^*X}$-module. Its characteristic cycle is a cycle of ![]() $T^*X$ which does not depend on a choice of filtration as above. It is the characteristic cycle of
$T^*X$ which does not depend on a choice of filtration as above. It is the characteristic cycle of ![]() $\mathcal {M}$. We denote it by
$\mathcal {M}$. We denote it by ![]() $CC(\mathcal {M})$. The support of
$CC(\mathcal {M})$. The support of ![]() $CC(\mathcal {M})$ is a closed conical subset of
$CC(\mathcal {M})$ is a closed conical subset of ![]() $T^*X$ called the singular support of
$T^*X$ called the singular support of ![]() $\mathcal {M}$. We denote it by
$\mathcal {M}$. We denote it by ![]() $SS(\mathcal {M})$.
$SS(\mathcal {M})$.
Remark 1.6 The formation of the characteristic cycle commutes with flat base change. In particular, it commutes with base field extension and analytification.
As a consequence of [Reference GabberGab81], we have the following.
Theorem 1.7 For any coherent ![]() ${D}_X$-module
${D}_X$-module ![]() $\mathcal {M}$, the irreducible components of
$\mathcal {M}$, the irreducible components of ![]() $SS(\mathcal {M})$ have dimension
$SS(\mathcal {M})$ have dimension ![]() $\geq \dim X$.
$\geq \dim X$.
Definition 1.8 We say that a coherent ![]() ${D}_X$-module
${D}_X$-module ![]() $\mathcal {M}$ is holonomic if
$\mathcal {M}$ is holonomic if ![]() $SS(\mathcal {M})$ has pure dimension
$SS(\mathcal {M})$ has pure dimension ![]() $\dim X$.
$\dim X$.
Holonomy is the correct finiteness condition for ![]() ${D}_X$-modules, as will be clear from Proposition 1.10 below.
${D}_X$-modules, as will be clear from Proposition 1.10 below.
1.6 De Rham cohomology
Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $0$. Let
$0$. Let ![]() $X$ be a smooth algebraic
$X$ be a smooth algebraic ![]() $k$-variety of dimension
$k$-variety of dimension ![]() $d$. Let
$d$. Let ![]() $\mathcal {M}$ be a
$\mathcal {M}$ be a ![]() $\mathcal {D}_X$-module. We denote by
$\mathcal {D}_X$-module. We denote by
the algebraic de Rham complex of ![]() $\mathcal {M}$, where
$\mathcal {M}$, where ![]() $\mathcal {M}$ lies in degree
$\mathcal {M}$ lies in degree ![]() $0$. The algebraic de Rham cohomology of
$0$. The algebraic de Rham cohomology of ![]() $\mathcal {M}$ is the cohomology of
$\mathcal {M}$ is the cohomology of ![]() $\operatorname {DR} \mathcal {M}$.
$\operatorname {DR} \mathcal {M}$.
If ![]() $k=\mathbb {C}$, let
$k=\mathbb {C}$, let ![]() $\mathcal {M}^{\operatorname {an}}$ be the analytification of
$\mathcal {M}^{\operatorname {an}}$ be the analytification of ![]() $\mathcal {M}$ and define similarly the analytic de Rham complex of
$\mathcal {M}$ and define similarly the analytic de Rham complex of ![]() $\mathcal {M}$. The analytic de Rham cohomology of
$\mathcal {M}$. The analytic de Rham cohomology of ![]() $\mathcal {M}$ is the cohomology of
$\mathcal {M}$ is the cohomology of ![]() $\operatorname {DR} \mathcal {M}^{\operatorname {an}}$.
$\operatorname {DR} \mathcal {M}^{\operatorname {an}}$.
In the proper complex setting, the GAGA theorem for quasi-coherent cohomology identifies algebraic and analytic de Rham cohomology. See [Reference DeligneDel70, 6.6.1]. This is the following.
Proposition 1.9 Let ![]() $X$ be a smooth projective variety over
$X$ be a smooth projective variety over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $\mathcal {M}$ be a quasi-coherent
$\mathcal {M}$ be a quasi-coherent ![]() $\mathcal {D}_X$-module. Then, the canonical comparison morphism
$\mathcal {D}_X$-module. Then, the canonical comparison morphism
is an isomorphism.
When holonomy is imposed, algebraic de Rham cohomology is finite dimensional even when the ambient variety is not proper.
Proposition 1.10 Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Then, for every integer
$\mathcal {D}_X$-module. Then, for every integer ![]() $n$, the space
$n$, the space ![]() $H^{n}(X,\operatorname {DR} \mathcal {M})$ is finite dimensional over
$H^{n}(X,\operatorname {DR} \mathcal {M})$ is finite dimensional over ![]() $k$ and vanishes if
$k$ and vanishes if ![]() $n\neq 0,\ldots, 2\dim X$.
$n\neq 0,\ldots, 2\dim X$.
Proof. Since the formation of the de Rham complex commutes with push-forward [Reference Hotta, Takeuchi and TanisakiHTT00, 4.2.5] and since holonomy is preserved under push-forward [Reference Hotta, Takeuchi and TanisakiHTT00, 3.2.3], we can at the cost of replacing ![]() $X$ by a smooth compactification suppose that
$X$ by a smooth compactification suppose that ![]() $X$ is proper over
$X$ is proper over ![]() $k$. From Remark 1.11, we reduce to the case where
$k$. From Remark 1.11, we reduce to the case where ![]() $k=\mathbb {C}$. From Proposition 1.9, we are left to prove a variant of Proposition 1.10 where now
$k=\mathbb {C}$. From Proposition 1.9, we are left to prove a variant of Proposition 1.10 where now ![]() $X$ is a smooth compact complex manifold and where
$X$ is a smooth compact complex manifold and where ![]() $\mathcal {M}$ is a holonomic
$\mathcal {M}$ is a holonomic ![]() $\mathcal {D}_X$-module. From Kashiwara's perversity theorem [Reference KashiwaraKas75], we are left to prove that for every perverse complex
$\mathcal {D}_X$-module. From Kashiwara's perversity theorem [Reference KashiwaraKas75], we are left to prove that for every perverse complex ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $X$, the
$X$, the ![]() $\mathbb {C}$-vector space
$\mathbb {C}$-vector space ![]() $H^{n}(X,\mathcal {F})$ is finite dimensional and vanishes if
$H^{n}(X,\mathcal {F})$ is finite dimensional and vanishes if ![]() $n\neq -\dim X,\ldots,\dim X$. This is a standard fact from the theory of perverse complexes [Reference Beilinson, Bernstein, Deligne and GabberBBDG18, 4.2.4].
$n\neq -\dim X,\ldots,\dim X$. This is a standard fact from the theory of perverse complexes [Reference Beilinson, Bernstein, Deligne and GabberBBDG18, 4.2.4].
Remark 1.11 As a consequence of the invariance of quasi-coherent cohomology under flat base change, de Rham cohomology is invariant under base field extensions.
1.7 The solution and the irregularity complexes
Let ![]() $X$ be a complex manifold of dimension
$X$ be a complex manifold of dimension ![]() $d$. Let
$d$. Let ![]() $\mathcal {M}$ be a
$\mathcal {M}$ be a ![]() $\mathcal {D}_X$-module. The solution complex of
$\mathcal {D}_X$-module. The solution complex of ![]() $\mathcal {M}$ is defined as
$\mathcal {M}$ is defined as
The following theorem is due to Kashiwara [Reference KashiwaraKas75].
Theorem 1.12 Let ![]() $X$ be a smooth complex manifold. Let
$X$ be a smooth complex manifold. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Then the complexes
$\mathcal {D}_X$-module. Then the complexes ![]() $\operatorname {Sol} \mathcal {M}[\dim X]$ and
$\operatorname {Sol} \mathcal {M}[\dim X]$ and ![]() $\operatorname {DR} \mathcal {M}[\dim X]$ are perverse complexes.
$\operatorname {DR} \mathcal {M}[\dim X]$ are perverse complexes.
Let ![]() $Z$ be a hypersurface in
$Z$ be a hypersurface in ![]() $X$. Let
$X$. Let ![]() $i: Z\to X$ be the inclusion. Let
$i: Z\to X$ be the inclusion. Let ![]() $\mathcal {M}(\ast Z)$ be the localization of
$\mathcal {M}(\ast Z)$ be the localization of ![]() $\mathcal {M}$ along
$\mathcal {M}$ along ![]() $Z$. Define the irregularity complex of
$Z$. Define the irregularity complex of ![]() $\mathcal {M}$ along
$\mathcal {M}$ along ![]() $Z$ by
$Z$ by
The following theorem is due to Mebkhout [Reference MebkhoutMeb90].
Theorem 1.13 Let ![]() $X$ be a complex manifold. Let
$X$ be a complex manifold. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Let
$\mathcal {D}_X$-module. Let ![]() $Z$ be a hypersurface in
$Z$ be a hypersurface in ![]() $X$. Then
$X$. Then ![]() $\operatorname {Irr}_Z^*\mathcal {M}[\dim X]$ is a perverse complex supported on
$\operatorname {Irr}_Z^*\mathcal {M}[\dim X]$ is a perverse complex supported on ![]() $Z$.
$Z$.
The de Rham and solution complexes are related under sheaf duality; see [Reference MebkhoutMeb82].
Theorem 1.14 Let ![]() $X$ be a complex manifold. Let
$X$ be a complex manifold. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. There is a canonical isomorphism of complexes
$\mathcal {D}_X$-module. There is a canonical isomorphism of complexes
in the derived category of complexes of sheaves.
1.8 Characteristic cycle and the de Rham and solution complexes
For a complex of sheaves ![]() $\mathcal {F}$ with bounded and constructible cohomology, Kashiwara and Schapira defined the characteristic cycle
$\mathcal {F}$ with bounded and constructible cohomology, Kashiwara and Schapira defined the characteristic cycle ![]() $CC(\mathcal {F})$ by means of microlocal analysis [Reference Kashiwara and SchapiraKS90]. The following theorem identifies the characteristic cycle of a holonomic
$CC(\mathcal {F})$ by means of microlocal analysis [Reference Kashiwara and SchapiraKS90]. The following theorem identifies the characteristic cycle of a holonomic ![]() $\mathcal {D}_X$-module with that of its solution complex. See [Reference Kashiwara and SchapiraKS90, 11.3.3] and [Reference DubsonDub84, Theorem 4].
$\mathcal {D}_X$-module with that of its solution complex. See [Reference Kashiwara and SchapiraKS90, 11.3.3] and [Reference DubsonDub84, Theorem 4].
Theorem 1.15 Let ![]() $X$ be a complex manifold. Let
$X$ be a complex manifold. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Then
$\mathcal {D}_X$-module. Then
In particular, the computation of ![]() $CC(\mathcal {M})$ can be reduced to a sheaf-theoretic question. If the singular support of
$CC(\mathcal {M})$ can be reduced to a sheaf-theoretic question. If the singular support of ![]() $\mathcal {M}$ is already known, the following theorem [Reference KashiwaraKas75, Theorem 3.5] tells us how to chop off
$\mathcal {M}$ is already known, the following theorem [Reference KashiwaraKas75, Theorem 3.5] tells us how to chop off ![]() $X$ in order to compute
$X$ in order to compute ![]() $CC(\operatorname {Sol} \mathcal {M})$.
$CC(\operatorname {Sol} \mathcal {M})$.
Theorem 1.16 Let ![]() $X$ be a complex manifold. Let
$X$ be a complex manifold. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Let
$\mathcal {D}_X$-module. Let ![]() $X_1,\ldots,X_n$ be a Whitney stratification of
$X_1,\ldots,X_n$ be a Whitney stratification of ![]() $X$ such that
$X$ such that ![]() $SS(\mathcal {M})$ lies in
$SS(\mathcal {M})$ lies in ![]() $\bigcup _{i=1}^n T^*_{X_i}X$. Then, the cohomology sheaves of
$\bigcup _{i=1}^n T^*_{X_i}X$. Then, the cohomology sheaves of ![]() $(\operatorname {Sol} \mathcal {M})|_{X_i}$ are local systems on
$(\operatorname {Sol} \mathcal {M})|_{X_i}$ are local systems on ![]() $X_i$,
$X_i$, ![]() $i=1,\ldots,n$.
$i=1,\ldots,n$.
From a cohomological perspective, computing the characteristic cycle is useful because of Kashiwara and Dubson's formula [Reference DubsonDub84]. See also [Reference LaumonLau83].
Theorem 1.17 Let ![]() $X$ be a proper complex manifold. Let
$X$ be a proper complex manifold. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Then, we have
$\mathcal {D}_X$-module. Then, we have
where ![]() $\chi (X,\operatorname {DR}\mathcal {M})$ denotes the Euler–Poincaré characteristic of
$\chi (X,\operatorname {DR}\mathcal {M})$ denotes the Euler–Poincaré characteristic of ![]() $\operatorname {DR}\mathcal {M}$ and where
$\operatorname {DR}\mathcal {M}$ and where ![]() $(-,-)_{T^*X}$ denotes the intersection number of cycles in
$(-,-)_{T^*X}$ denotes the intersection number of cycles in ![]() $T^*X$.
$T^*X$.
1.9 Characteristic cycle and functorialities
The characteristic cycle for ![]() $\mathcal {D}$-modules commutes with proper push-forward. This is the following.
$\mathcal {D}$-modules commutes with proper push-forward. This is the following.
Lemma 1.18 Let ![]() $f: X\to Y$ be a proper morphism between smooth varieties over
$f: X\to Y$ be a proper morphism between smooth varieties over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Then,
$\mathcal {D}_X$-module. Then, ![]() $CC(f_+\mathcal {M})=f_*CC(\mathcal {M})$.
$CC(f_+\mathcal {M})=f_*CC(\mathcal {M})$.
Proof. From Remark 1.6, we can suppose ![]() $k=\mathbb {C}$. We have the following chain of equalities:
$k=\mathbb {C}$. We have the following chain of equalities:
The first equality follows from Remark 1.6 applied to ![]() $f_+\mathcal {M}$. The second equality follows from Theorem 1.15. The third equality follows from the compatibility of the formation of
$f_+\mathcal {M}$. The second equality follows from Theorem 1.15. The third equality follows from the compatibility of the formation of ![]() $\operatorname {Sol}$ with proper push-forward. The fourth equality follows from [Reference Kashiwara and SchapiraKS90, 9.4.2]. The last equality follows from the above arguments applied to
$\operatorname {Sol}$ with proper push-forward. The fourth equality follows from [Reference Kashiwara and SchapiraKS90, 9.4.2]. The last equality follows from the above arguments applied to ![]() $\mathcal {M}$.
$\mathcal {M}$.
Definition 1.19 Let ![]() $f: Y\to X$ be a morphism between smooth varieties over
$f: Y\to X$ be a morphism between smooth varieties over ![]() $k$ or between complex manifolds. Let
$k$ or between complex manifolds. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. We say that
$\mathcal {D}_X$-module. We say that ![]() $f: Y\to X$ is non-characteristic for
$f: Y\to X$ is non-characteristic for ![]() $\mathcal {M}$ if it is
$\mathcal {M}$ if it is ![]() $SS(\mathcal {M})$-transversal.
$SS(\mathcal {M})$-transversal.
The following results are due to Kashiwara [Reference KashiwaraKas95].
Theorem 1.20 Let ![]() $f: Y\to X$ be a morphism between smooth varieties over
$f: Y\to X$ be a morphism between smooth varieties over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module such that
$\mathcal {D}_X$-module such that ![]() $f: Y\to X$ is non-characteristic for
$f: Y\to X$ is non-characteristic for ![]() $\mathcal {M}$. Then the following statements hold.
$\mathcal {M}$. Then the following statements hold.
(i) The
 $\mathcal {D}_Y$-module pull-back
$\mathcal {D}_Y$-module pull-back  $f^+\mathcal {M}$ is concentrated in degree
$f^+\mathcal {M}$ is concentrated in degree  $0$. That is,
$0$. That is,  $f^+\mathcal {M}\simeq f^* \mathcal {M}$.
$f^+\mathcal {M}\simeq f^* \mathcal {M}$.(ii) We have
 $SS(f^+\mathcal {M} )=f^\circ SS(\mathcal {M})$.
$SS(f^+\mathcal {M} )=f^\circ SS(\mathcal {M})$.(iii) If
 $k=\mathbb {C}$, the comparison morphisms
are isomorphisms in the derived category of sheaves.
$k=\mathbb {C}$, the comparison morphisms
are isomorphisms in the derived category of sheaves. \[ f^* \operatorname{Sol} \mathcal{M}^{\operatorname{an}} \longrightarrow \operatorname{Sol} f^+\mathcal{M}^{\operatorname{an}} \quad \text{and} \quad \operatorname{DR} f^+\mathcal{M}^{\operatorname{an}} \longrightarrow f^* \operatorname{DR}\mathcal{M}^{\operatorname{an}} \]
\[ f^* \operatorname{Sol} \mathcal{M}^{\operatorname{an}} \longrightarrow \operatorname{Sol} f^+\mathcal{M}^{\operatorname{an}} \quad \text{and} \quad \operatorname{DR} f^+\mathcal{M}^{\operatorname{an}} \longrightarrow f^* \operatorname{DR}\mathcal{M}^{\operatorname{an}} \]
1.10 Meromorphic flat connections
Let ![]() $X$ be a smooth algebraic variety over
$X$ be a smooth algebraic variety over ![]() $k$. A flat connection on
$k$. A flat connection on ![]() $X$ or module with integrable connection on
$X$ or module with integrable connection on ![]() $X$ is a
$X$ is a ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $\mathcal {E}:=(E,\nabla )$ whose underlying
$\mathcal {E}:=(E,\nabla )$ whose underlying ![]() $\mathcal {O}_X$-module
$\mathcal {O}_X$-module ![]() $E$ is a vector bundle of finite rank on
$E$ is a vector bundle of finite rank on ![]() $X$. We denote by
$X$. We denote by ![]() $\operatorname {MIC}(X)$ the category of flat connections on
$\operatorname {MIC}(X)$ the category of flat connections on ![]() $X$.
$X$.
If ![]() $D$ is a divisor in
$D$ is a divisor in ![]() $X$, a meromorphic flat connection on
$X$, a meromorphic flat connection on ![]() $X$ with poles along
$X$ with poles along ![]() $D$ is a
$D$ is a ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $\mathcal {M}:=(M,\nabla )$ whose underlying
$\mathcal {M}:=(M,\nabla )$ whose underlying ![]() $\mathcal {O}_X$-module
$\mathcal {O}_X$-module ![]() $M$ is a locally free sheaf of
$M$ is a locally free sheaf of ![]() $\mathcal {O}_X(\ast D)$-modules of finite rank. We denote by
$\mathcal {O}_X(\ast D)$-modules of finite rank. We denote by ![]() $\operatorname {MIC}(X,D)$ the category of meromorphic flat connections on
$\operatorname {MIC}(X,D)$ the category of meromorphic flat connections on ![]() $X$ with poles along
$X$ with poles along ![]() $D$.
$D$.
Remark 1.21 The above definitions make sense in the analytic setting, where the same notation will be used.
Remark 1.22 Meromorphic flat connections are holonomic ![]() $\mathcal {D}$-modules.
$\mathcal {D}$-modules.
In the algebraic setting, there is no difference between flat connections and meromorphic flat connections. This is expressed by the following proposition [Reference Hotta, Takeuchi and TanisakiHTT00, 5.3.1].
Proposition 1.23 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$. Let
$k$. Let ![]() $j: U=X\setminus D\to X$ be the inclusion. Then
$j: U=X\setminus D\to X$ be the inclusion. Then ![]() $(j_*, j^*)$ induce an equivalence of categories between
$(j_*, j^*)$ induce an equivalence of categories between ![]() $\operatorname {MIC}(U)$ and
$\operatorname {MIC}(U)$ and ![]() $\operatorname {MIC}(X,D)$.
$\operatorname {MIC}(X,D)$.
Since all the action in this paper happens at infinity, we will use the meromorphic viewpoint. The next lemma says that this does not make any difference for cohomology.
Lemma 1.24 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$. Put
$k$. Put ![]() $U:=X\setminus D$ and let
$U:=X\setminus D$ and let ![]() $j: U\to X$ be the inclusion. Let
$j: U\to X$ be the inclusion. Let ![]() $\mathcal {E}$ be an object in
$\mathcal {E}$ be an object in ![]() $\operatorname {MIC}(U)$. Then the canonical restriction morphism
$\operatorname {MIC}(U)$. Then the canonical restriction morphism
is an isomorphism in the derived category of vector spaces over ![]() $k$.
$k$.
Proof. We have
where the second equality comes from the fact that ![]() $j$ is an affine morphism, and where the last equality follows from
$j$ is an affine morphism, and where the last equality follows from ![]() $j_*\operatorname {DR} \mathcal {E}\simeq \operatorname {DR} j_*\mathcal {E}$.
$j_*\operatorname {DR} \mathcal {E}\simeq \operatorname {DR} j_*\mathcal {E}$.
Proposition 1.25 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ be objects of
$\mathcal {M}_2$ be objects of ![]() $\operatorname {MIC}(X,D)$. Then, there is a canonical isomorphism
$\operatorname {MIC}(X,D)$. Then, there is a canonical isomorphism
in the derived category of ![]() $k$-vector spaces.
$k$-vector spaces.
Proof. Combining [Reference BorelBor87, VII 9.8] and [Reference BorelBor87, VI 5.3.2] yields a canonical isomorphism
where ![]() $\mathcal {M}_1^{\vee }$ denotes the
$\mathcal {M}_1^{\vee }$ denotes the ![]() $\mathcal {D}_X$-module dual to
$\mathcal {D}_X$-module dual to ![]() $\mathcal {M}_1$. Since
$\mathcal {M}_1$. Since ![]() $\mathcal {M}_2$ is a locally free
$\mathcal {M}_2$ is a locally free ![]() $\mathcal {O}_X$-module localized along
$\mathcal {O}_X$-module localized along ![]() $D$, we have
$D$, we have
Observe that ![]() $\mathcal {M}_1^{\vee }(\ast D)$ is an object of
$\mathcal {M}_1^{\vee }(\ast D)$ is an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $\mathcal {M}_1^*$ be the meromorphic connection dual to
$\mathcal {M}_1^*$ be the meromorphic connection dual to ![]() $\mathcal {M}_1$. Then [Reference Hotta, Takeuchi and TanisakiHTT00, 2.6.10] ensures that the restriction of
$\mathcal {M}_1$. Then [Reference Hotta, Takeuchi and TanisakiHTT00, 2.6.10] ensures that the restriction of ![]() $\mathcal {M}_1^{\vee }(\ast D)$ and
$\mathcal {M}_1^{\vee }(\ast D)$ and ![]() $\mathcal {M}_1^*$ to
$\mathcal {M}_1^*$ to ![]() $U:=X\setminus D$ are canonically isomorphic. From Proposition 1.23, we deduce that
$U:=X\setminus D$ are canonically isomorphic. From Proposition 1.23, we deduce that ![]() $\mathcal {M}_1^{\vee }(\ast D)$ and
$\mathcal {M}_1^{\vee }(\ast D)$ and ![]() $\mathcal {M}_1^*$ are canonically isomorphic. We thus conclude the proof of Proposition 1.25 using the identification
$\mathcal {M}_1^*$ are canonically isomorphic. We thus conclude the proof of Proposition 1.25 using the identification ![]() $\mathcal {M}_1^{\ast }\otimes _{\mathcal {O}_X} \mathcal {M}_2\simeq {\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1,\mathcal {M}_2)$.
$\mathcal {M}_1^{\ast }\otimes _{\mathcal {O}_X} \mathcal {M}_2\simeq {\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1,\mathcal {M}_2)$.
1.11 Good formal structure for connections
In the next definition, we follow [Reference KedlayaKed21, Definition 2.1.3] and fix a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $0$.
$0$.
Definition 1.26 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. We say that
$\operatorname {MIC}(X,D)$. We say that ![]() $\mathcal {M}$ has good formal structure at
$\mathcal {M}$ has good formal structure at ![]() $x\in D$ if there is a decomposition
$x\in D$ if there is a decomposition
where
(1) the ring
 $\widehat {\mathcal {O}}_{X,x}(\ast D)$ is the localization along
$\widehat {\mathcal {O}}_{X,x}(\ast D)$ is the localization along  $D$ of the completion of
$D$ of the completion of  ${\mathcal {O}}_{X,x}$ along the intersection of the irreducible components of
${\mathcal {O}}_{X,x}$ along the intersection of the irreducible components of  $D$ containing
$D$ containing  $x$ and
$x$ and  $\mathcal {S}$ is a finite étale
$\mathcal {S}$ is a finite étale  $\widehat {\mathcal {O}}_{X,x}(\ast D)$-algebra;
$\widehat {\mathcal {O}}_{X,x}(\ast D)$-algebra;(2)
 $I$ is a finite set;
$I$ is a finite set;(3) each
 $\mathcal {R}_{\alpha }$ is a regular differential module over
$\mathcal {R}_{\alpha }$ is a regular differential module over  $\mathcal {S}$;
$\mathcal {S}$;(4)
 $\varphi _\alpha$
$\varphi _\alpha$  $(\alpha \in I)$ are elements in
$(\alpha \in I)$ are elements in  $\mathcal {S}$ satisfying that, if
$\mathcal {S}$ satisfying that, if  $\varphi _\alpha$ does not lie in the integral closure
$\varphi _\alpha$ does not lie in the integral closure  $\mathcal {S}_0$ of
$\mathcal {S}_0$ of  $\mathcal {O}_{X,x}$ in
$\mathcal {O}_{X,x}$ in  $\mathcal {S}$, then
$\mathcal {S}$, then  $\varphi _\alpha$ is a unit of
$\varphi _\alpha$ is a unit of  $\mathcal {S}$ and
$\mathcal {S}$ and  $\varphi _\alpha ^{-1}\in \mathcal {S}_0$; furthermore, if
$\varphi _\alpha ^{-1}\in \mathcal {S}_0$; furthermore, if  $\varphi _\alpha -\varphi _\beta$ does not lie in
$\varphi _\alpha -\varphi _\beta$ does not lie in  $\mathcal {S}_0$, then
$\mathcal {S}_0$, then  $\varphi _\alpha -\varphi _\beta$ is a unit of
$\varphi _\alpha -\varphi _\beta$ is a unit of  $\mathcal {S}$ and
$\mathcal {S}$ and  $(\varphi _\alpha -\varphi _\beta )^{-1}\in \mathcal {S}_0$.
$(\varphi _\alpha -\varphi _\beta )^{-1}\in \mathcal {S}_0$.
Definition 1.28 Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. We say that a point
$\operatorname {MIC}(X,D)$. We say that a point ![]() $x$ of
$x$ of ![]() $D$ is a turning point of
$D$ is a turning point of ![]() $\mathcal {M}$ if
$\mathcal {M}$ if ![]() $\mathcal {M}$ does not admit a good formal structure at
$\mathcal {M}$ does not admit a good formal structure at ![]() $x$. The set of turning points of
$x$. The set of turning points of ![]() $\mathcal {M}$ is called the turning locus of
$\mathcal {M}$ is called the turning locus of ![]() $\mathcal {M}$. We denote it by
$\mathcal {M}$. We denote it by ![]() $\operatorname {TL}(\mathcal {M})$. If
$\operatorname {TL}(\mathcal {M})$. If ![]() $\operatorname {TL}(\mathcal {M})$ is empty, we say that
$\operatorname {TL}(\mathcal {M})$ is empty, we say that ![]() $\mathcal {M}$ admits good formal structure along
$\mathcal {M}$ admits good formal structure along ![]() $D$.
$D$.
Remark 1.29 The formation of the turning locus commutes with regular base change. See [Reference KedlayaKed21, 4.3.2] for a proof.
The compatibility of good formal structure and pull-back follows from Definition 1.26:
Proposition 1.30 Let ![]() $f: (Y,E)\to (X,D)$ be a morphism of normal crossing pairs over
$f: (Y,E)\to (X,D)$ be a morphism of normal crossing pairs over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $x$ be a point in
$x$ be a point in ![]() $E$ such that
$E$ such that ![]() $\mathcal {M}$ has good formal structure at
$\mathcal {M}$ has good formal structure at ![]() $f(x)$. Then,
$f(x)$. Then, ![]() $f^+\mathcal {M}$ has good formal structure at
$f^+\mathcal {M}$ has good formal structure at ![]() $x$. In particular, if
$x$. In particular, if ![]() $\mathcal {M}$ has good formal structure, so does
$\mathcal {M}$ has good formal structure, so does ![]() $f^+\mathcal {M}$.
$f^+\mathcal {M}$.
Purity of the turning locus was proved by André when ![]() $D$ is smooth [Reference AndréAnd07, 3.4.3] and by Kedlaya when
$D$ is smooth [Reference AndréAnd07, 3.4.3] and by Kedlaya when ![]() $D$ has normal crossing [Reference KedlayaKed21, 2.3.1].
$D$ has normal crossing [Reference KedlayaKed21, 2.3.1].
Theorem 1.31 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Then, for any object
$k$. Then, for any object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}(X,D)$, the turning locus of
$\operatorname {MIC}(X,D)$, the turning locus of ![]() $\mathcal {M}$ is a closed subscheme of
$\mathcal {M}$ is a closed subscheme of ![]() $D$ of pure codimension
$D$ of pure codimension ![]() $1$.
$1$.
The following fundamental theorem was proved by Kedlaya [Reference KedlayaKed11, Theorem 8.1.3] and Mochizuki [Reference MochizukiMoc11, Theorem 19.5] with complement from [Reference KedlayaKed21, Corollary 3.2.5].
Theorem 1.32 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then, there exists a morphism of smooth algebraic varieties
$\operatorname {MIC}(X,D)$. Then, there exists a morphism of smooth algebraic varieties ![]() $f:Y\to X$ obtained as a composition of blow-up with smooth centres above
$f:Y\to X$ obtained as a composition of blow-up with smooth centres above ![]() $\operatorname {TL}(\mathcal {M})$ such that
$\operatorname {TL}(\mathcal {M})$ such that ![]() $f^{-1}(D)$ is a normal crossing divisor of
$f^{-1}(D)$ is a normal crossing divisor of ![]() $Y$ and
$Y$ and ![]() $f^+\mathcal {M}$ admits good formal structure along
$f^+\mathcal {M}$ admits good formal structure along ![]() $f^{-1}(D)$.
$f^{-1}(D)$.
We thank the anonymous referee for pointing out the following.
Remark 1.33 In Theorem 1.32, it is not obvious from [Reference KedlayaKed11, Theorem 8.1.3] and [Reference MochizukiMoc11, Theorem 19.5] that ![]() $f:Y\to X$ can be taken as a composition of blow-up with smooth centres above
$f:Y\to X$ can be taken as a composition of blow-up with smooth centres above ![]() $\operatorname {TL}(\mathcal {M})$. Such control on
$\operatorname {TL}(\mathcal {M})$. Such control on ![]() $f$ is guaranteed by the subsequent results from [Reference KedlayaKed21].
$f$ is guaranteed by the subsequent results from [Reference KedlayaKed21].
1.12 Irregularity number
Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$ of dimension
$k$ of dimension ![]() $d+1\geq 1$. Let
$d+1\geq 1$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. In the setting of Definition 1.26, good formal structure always holds at the generic point
$\operatorname {MIC}(X,D)$. In the setting of Definition 1.26, good formal structure always holds at the generic point ![]() $\eta$ of an irreducible component
$\eta$ of an irreducible component ![]() $Z$ of
$Z$ of ![]() $D$. In that case,
$D$. In that case, ![]() $\widehat {\mathcal {O}}_{X,\eta }(\ast D)$ has the form
$\widehat {\mathcal {O}}_{X,\eta }(\ast D)$ has the form ![]() $k[\![ x_1,\ldots,x_d,y]\!] [y^{-1}]$ and
$k[\![ x_1,\ldots,x_d,y]\!] [y^{-1}]$ and ![]() $S$ has the form
$S$ has the form ![]() $K [\![ x_1,\ldots, x_d,y^{1/m}]\!] [(y^{1/m})^{-1}]$ where
$K [\![ x_1,\ldots, x_d,y^{1/m}]\!] [(y^{1/m})^{-1}]$ where ![]() $m\geq 1$ and where
$m\geq 1$ and where ![]() $K/k$ is a finite extension.
$K/k$ is a finite extension.
Definition 1.34 For an object ![]() $\mathcal {M}$ in
$\mathcal {M}$ in ![]() $\operatorname {MIC}(X,D)$, the generic slopes of
$\operatorname {MIC}(X,D)$, the generic slopes of ![]() $\mathcal {M}$ along
$\mathcal {M}$ along ![]() $Z$ are the poles orders in the
$Z$ are the poles orders in the ![]() $y$-variable of the
$y$-variable of the ![]() $\varphi _\alpha$ contributing to (1.27). Let us denote them by
$\varphi _\alpha$ contributing to (1.27). Let us denote them by ![]() $\operatorname {ord}_y \varphi _\alpha$ where
$\operatorname {ord}_y \varphi _\alpha$ where ![]() $\alpha \in I$ and put
$\alpha \in I$ and put
The generic irregularity number of ![]() $\mathcal {M}$ along
$\mathcal {M}$ along ![]() $Z$ is defined as
$Z$ is defined as
Remark 1.35 In the setting of Definition 1.34, the generic irregularity number of ![]() $\mathcal {M}$ along
$\mathcal {M}$ along ![]() $Z$ is an integer independent of the choice of the finite étale
$Z$ is an integer independent of the choice of the finite étale ![]() $\widehat {\mathcal {O}}_{X,\eta }(\ast D)$-algebra
$\widehat {\mathcal {O}}_{X,\eta }(\ast D)$-algebra ![]() $S$.
$S$.
In general, irregularity numbers and irregularity complexes are related through a theorem of Malgrange [Reference MalgrangeMal71, Theorem 1.4]. We record it in the following form useful for us.
Lemma 1.36 Let ![]() $(X,D)$ be an analytic pair. Let
$(X,D)$ be an analytic pair. Let ![]() $Z$ be an irreducible component of
$Z$ be an irreducible component of ![]() $D$. Let
$D$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then, the generic irregularity number of
$\operatorname {MIC}(X,D)$. Then, the generic irregularity number of ![]() $\mathcal {M}$ along
$\mathcal {M}$ along ![]() $Z$ is the generic rank along
$Z$ is the generic rank along ![]() $Z$ of the perverse complex
$Z$ of the perverse complex ![]() $\operatorname {Irr}^*_{D} \mathcal {M}$.
$\operatorname {Irr}^*_{D} \mathcal {M}$.
1.13  $b$-divisors
$b$-divisors
Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$. A modification of
$k$. A modification of ![]() $X$ is the datum of a smooth variety
$X$ is the datum of a smooth variety ![]() $Y$ over
$Y$ over ![]() $k$ and a map
$k$ and a map ![]() $Y\to X$ which is proper, dominant and an isomorphism away from a nowhere-dense closed subset of
$Y\to X$ which is proper, dominant and an isomorphism away from a nowhere-dense closed subset of ![]() $X$. Following [Reference KedlayaKed21], we introduce the following definition.
$X$. Following [Reference KedlayaKed21], we introduce the following definition.
Definition 1.37 The group of integral ![]() $b$-divisors
$b$-divisors ![]() $\textbf {Div}(X)$ of
$\textbf {Div}(X)$ of ![]() $X$ is the limit
$X$ is the limit
where ![]() $Y\to X$ runs over the category of modifications of
$Y\to X$ runs over the category of modifications of ![]() $X$ and where the transition maps are push-forward.
$X$ and where the transition maps are push-forward.
For ![]() $D$ in
$D$ in ![]() $\textbf {Div}(X)$, we denote by
$\textbf {Div}(X)$, we denote by ![]() $D(Y)$ the component of
$D(Y)$ the component of ![]() $D$ along a modification
$D$ along a modification ![]() $Y\to X$. For every irreducible divisor
$Y\to X$. For every irreducible divisor ![]() $E$ of
$E$ of ![]() $Y$, we denote by
$Y$, we denote by ![]() $m(E,D)$ the multiplicity of
$m(E,D)$ the multiplicity of ![]() $D(Y)$ along
$D(Y)$ along ![]() $E$.
$E$.
Definition 1.38 The group of integral Cartier ![]() $b$-divisors
$b$-divisors ![]() $\textbf {CDiv}(X)$ on
$\textbf {CDiv}(X)$ on ![]() $X$ is the colimit
$X$ is the colimit
where ![]() $Y\to X$ runs over the category of modifications of
$Y\to X$ runs over the category of modifications of ![]() $X$ and where the transition maps are pull-back.
$X$ and where the transition maps are pull-back.
Let ![]() $\operatorname {ZR}^{\operatorname {divis}}(X)$ be the subset of the Zariski–Riemann space of
$\operatorname {ZR}^{\operatorname {divis}}(X)$ be the subset of the Zariski–Riemann space of ![]() $X$ consisting of divisorial valuations centred on
$X$ consisting of divisorial valuations centred on ![]() $X$. As explained in [Reference KedlayaKed21], the group of integral
$X$. As explained in [Reference KedlayaKed21], the group of integral ![]() $b$-divisors identifies with the set of functions
$b$-divisors identifies with the set of functions ![]() $m : \operatorname {ZR}^{\operatorname {divis}}(X)\to \mathbb {Z}$ such that for every modification
$m : \operatorname {ZR}^{\operatorname {divis}}(X)\to \mathbb {Z}$ such that for every modification ![]() $Y\to X$, there is only a finite number of divisorial valuations
$Y\to X$, there is only a finite number of divisorial valuations ![]() $v\in \operatorname {ZR}^{\operatorname {divis}}(X)$ centred at an irreducible divisor of
$v\in \operatorname {ZR}^{\operatorname {divis}}(X)$ centred at an irreducible divisor of ![]() $Y$ such that
$Y$ such that ![]() $m(v)\neq 0$. Thus, the order on
$m(v)\neq 0$. Thus, the order on ![]() $\mathbb {Z}$ induces an order
$\mathbb {Z}$ induces an order ![]() $\leq$ on
$\leq$ on ![]() $\textbf {Div}(X)$. Furthermore, there is a canonical injective map
$\textbf {Div}(X)$. Furthermore, there is a canonical injective map
One of the main players of this paper is a Cartier ![]() $b$-divisor with an extra property called nef in [Reference KedlayaKed21]. In view of Lemmas 1.4.9 and 1.4.10 from [Reference KedlayaKed21], we can define nef Cartier
$b$-divisor with an extra property called nef in [Reference KedlayaKed21]. In view of Lemmas 1.4.9 and 1.4.10 from [Reference KedlayaKed21], we can define nef Cartier ![]() $b$-divisor as follows.
$b$-divisor as follows.
Definition 1.39 Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$. Let
$k$. Let ![]() $D$ be a Cartier
$D$ be a Cartier ![]() $b$-divisor on
$b$-divisor on ![]() $X$. We say that
$X$. We say that ![]() $D$ is nef if for every modification
$D$ is nef if for every modification ![]() $Y\to X$, we have
$Y\to X$, we have ![]() $D\leq D(Y)$ in
$D\leq D(Y)$ in ![]() $\textbf {Div}(X)$ where
$\textbf {Div}(X)$ where ![]() $D(Y)$ is viewed as a
$D(Y)$ is viewed as a ![]() $b$-divisor via
$b$-divisor via ![]() $\textbf {CDiv}(X) \to \textbf {Div}(X)$.
$\textbf {CDiv}(X) \to \textbf {Div}(X)$.
1.14 The irregularity  $b$-divisor
$b$-divisor
Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$. We recall the following definition from [Reference KedlayaKed21, 3.1.1].
$k$. We recall the following definition from [Reference KedlayaKed21, 3.1.1].
Definition 1.40 Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. We denote by
$\operatorname {MIC}(X,D)$. We denote by ![]() $\operatorname {Irr} \mathcal {M}$ the unique
$\operatorname {Irr} \mathcal {M}$ the unique ![]() $b$-divisor on
$b$-divisor on ![]() $X$ such that for every modification
$X$ such that for every modification ![]() $p: Y\to X$, the multiplicity of
$p: Y\to X$, the multiplicity of ![]() $\operatorname {Irr} \mathcal {M}$ along an irreducible divisor
$\operatorname {Irr} \mathcal {M}$ along an irreducible divisor ![]() $E$ of
$E$ of ![]() $Y$ is the generic irregularity
$Y$ is the generic irregularity ![]() $\operatorname {irr}(E,p^+\mathcal {M})$ of
$\operatorname {irr}(E,p^+\mathcal {M})$ of ![]() $p^{+}\mathcal {M}$ along
$p^{+}\mathcal {M}$ along ![]() $E$. We put
$E$. We put
The following lemma is obvious.
Lemma 1.41 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$. Let
$k$. Let ![]() $k\subset K$ be a field extension. Let
$k\subset K$ be a field extension. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then,
$\operatorname {MIC}(X,D)$. Then, ![]() $\operatorname {Irr}(X_K,\mathcal {M}_K)=\operatorname {Irr}(X,\mathcal {M})_K$.
$\operatorname {Irr}(X_K,\mathcal {M}_K)=\operatorname {Irr}(X,\mathcal {M})_K$.
Remark 1.42 In the setting of Definition 1.40, one can also define ![]() $R(\mathcal {M})$ the unique rational
$R(\mathcal {M})$ the unique rational ![]() $b$-divisor on
$b$-divisor on ![]() $X$ such that for every modification
$X$ such that for every modification ![]() $p: Y\to X$, the multiplicity of
$p: Y\to X$, the multiplicity of ![]() $R(\mathcal {M})$ along an irreducible divisor
$R(\mathcal {M})$ along an irreducible divisor ![]() $E$ of
$E$ of ![]() $Y$ is the highest generic slope
$Y$ is the highest generic slope ![]() $r(E,p^+\mathcal {M})\in \mathbb {Q}_{\geq 0}$ of
$r(E,p^+\mathcal {M})\in \mathbb {Q}_{\geq 0}$ of ![]() $p^{+}\mathcal {M}$ along
$p^{+}\mathcal {M}$ along ![]() $E$, and put
$E$, and put ![]() $R(Y,p^+\mathcal {M}):=(R(\mathcal {M}))(Y) \text { in } \operatorname {Div}(Y)_{\mathbb {Q}}$.
$R(Y,p^+\mathcal {M}):=(R(\mathcal {M}))(Y) \text { in } \operatorname {Div}(Y)_{\mathbb {Q}}$.
Remark 1.43 Equivalently, the ![]() $b$-divisors
$b$-divisors ![]() $R(\mathcal {M})$ and
$R(\mathcal {M})$ and ![]() $\operatorname {Irr} \mathcal {M}$ will be viewed as
$\operatorname {Irr} \mathcal {M}$ will be viewed as ![]() $\mathbb {Q}$-valued functions on the set of divisorial valuations of
$\mathbb {Q}$-valued functions on the set of divisorial valuations of ![]() $X$.
$X$.
The following theorem is due to Kedlaya [Reference KedlayaKed21, 3.2.3].
Theorem 1.44 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. For any object
$k$. For any object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}(X,D)$, the
$\operatorname {MIC}(X,D)$, the ![]() $b$-divisor
$b$-divisor ![]() $\operatorname {Irr} \mathcal {M}$ is a nef Cartier
$\operatorname {Irr} \mathcal {M}$ is a nef Cartier ![]() $b$-divisor. In particular, we have
$b$-divisor. In particular, we have
in ![]() $\textbf {Div}(X)$, where
$\textbf {Div}(X)$, where ![]() $\operatorname {Irr}(X,\mathcal {M})$ is viewed as a
$\operatorname {Irr}(X,\mathcal {M})$ is viewed as a ![]() $b$-divisor via
$b$-divisor via ![]() $\textbf {CDiv}(X) \to \textbf {Div}(X)$.
$\textbf {CDiv}(X) \to \textbf {Div}(X)$.
Corollary 1.45 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $\mathcal {M}$ be an object in
$\mathcal {M}$ be an object in ![]() $\operatorname {MIC}(X,D)$. Then the following conditions are equivalent:
$\operatorname {MIC}(X,D)$. Then the following conditions are equivalent:
(i)
 $\operatorname {Irr}(X,\mathcal {M})\leq R$ in
$\operatorname {Irr}(X,\mathcal {M})\leq R$ in  $\operatorname {Div}(X)$;
$\operatorname {Div}(X)$;(ii) for every point
 $0$ in
$0$ in  $D$, for every locally closed smooth curve
$D$, for every locally closed smooth curve  $C \to X$ in
$C \to X$ in  $X$ meeting
$X$ meeting  $D$ at
$D$ at  $0$ only, we have
where
$0$ only, we have
where \[ \operatorname{irr}(0,\mathcal{M}|_{C})\leq (C,R)_0 \]
\[ \operatorname{irr}(0,\mathcal{M}|_{C})\leq (C,R)_0 \]
 $(C,R)_0$ denotes the intersection number of
$(C,R)_0$ denotes the intersection number of  $C$ with
$C$ with  $R$ at
$R$ at  $0$.
$0$.
Proof. If condition (ii) holds, we get condition (i) by using generically enough smooth curves transverse to the irreducible components of ![]() $D$. We now show that condition (i) implies condition (ii). To do this, we can suppose that
$D$. We now show that condition (i) implies condition (ii). To do this, we can suppose that ![]() $R=\operatorname {Irr}(X,\mathcal {M})$. Let
$R=\operatorname {Irr}(X,\mathcal {M})$. Let ![]() $0$ be a point in
$0$ be a point in ![]() $D$ and let
$D$ and let ![]() $C \to X$ be a locally closed smooth curve meeting
$C \to X$ be a locally closed smooth curve meeting ![]() $D$ at
$D$ at ![]() $0$ only. Let
$0$ only. Let ![]() $p : Y\to X$ be a modification of
$p : Y\to X$ be a modification of ![]() $X$ which is an isomorphism above
$X$ which is an isomorphism above ![]() $X\setminus D$. By valuative criterion for properness, the immersion
$X\setminus D$. By valuative criterion for properness, the immersion ![]() $C\to X$ factors uniquely through an immersion
$C\to X$ factors uniquely through an immersion ![]() $C\to Y$ followed by
$C\to Y$ followed by ![]() $p$. In particular, we have
$p$. In particular, we have
On the other hand, the projection formula yields
From Theorem 1.44, we further have
in ![]() $\operatorname {Div}(Y)$. Hence, the sought-after inequality for
$\operatorname {Div}(Y)$. Hence, the sought-after inequality for ![]() $X, \mathcal {M}, C\to X$ and
$X, \mathcal {M}, C\to X$ and ![]() $R=\operatorname {Irr}(X,\mathcal {M})$ follows from the analogous inequality for
$R=\operatorname {Irr}(X,\mathcal {M})$ follows from the analogous inequality for ![]() $Y, p^+\mathcal {M}, C\to Y$ and
$Y, p^+\mathcal {M}, C\to Y$ and ![]() $R=\operatorname {Irr}(Y,p^+\mathcal {M})$. From Theorem 1.32, we are thus left to suppose that
$R=\operatorname {Irr}(Y,p^+\mathcal {M})$. From Theorem 1.32, we are thus left to suppose that ![]() $\mathcal {M}$ has good formal structure and that
$\mathcal {M}$ has good formal structure and that ![]() $C$ is transverse to
$C$ is transverse to ![]() $D$ at
$D$ at ![]() $0$. In that case, the sought-after inequality is an equality.
$0$. In that case, the sought-after inequality is an equality.
Remark 1.46 For surfaces, Corollary 1.45 was proved by Sabbah [Reference SabbahSab00, 3.2.3].
The property of having good formal structure can be read from the irregularity ![]() $b$-divisor. This is due to Kedlaya [Reference KedlayaKed21, 3.1.2] as a consequence of Theorem 1.44.
$b$-divisor. This is due to Kedlaya [Reference KedlayaKed21, 3.1.2] as a consequence of Theorem 1.44.
Theorem 1.47 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then,
$\operatorname {MIC}(X,D)$. Then, ![]() $\mathcal {M}$ has good formal structure if and only if
$\mathcal {M}$ has good formal structure if and only if
in ![]() $\textbf {Div}(X)$.
$\textbf {Div}(X)$.
The proof of Corollary 1.45 combined with Theorem 1.47 yields the following curve-like criterion for testing good formal structure.
Corollary 1.48 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Then, an object
$k$. Then, an object ![]() $\mathcal {M}$ in
$\mathcal {M}$ in ![]() $\operatorname {MIC}(X,D)$ has good formal structure if and only if for every point
$\operatorname {MIC}(X,D)$ has good formal structure if and only if for every point ![]() $0$ in
$0$ in ![]() $D$, for every locally closed smooth curve
$D$, for every locally closed smooth curve ![]() $C \to X$ in
$C \to X$ in ![]() $X$ meeting
$X$ meeting ![]() $D$ at
$D$ at ![]() $0$ only, we have
$0$ only, we have
Putting Corollaries 1.45 and 1.48 together yields the following differential analogue of a result [Reference HuHu19] of the first named author.
Corollary 1.49 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$ where
$k$ where ![]() $D$ is smooth and irreducible. Let
$D$ is smooth and irreducible. Let ![]() $\mathcal {M}$ be an object in
$\mathcal {M}$ be an object in ![]() $\operatorname {MIC}(X,D)$. Then,
$\operatorname {MIC}(X,D)$. Then,
where ![]() $0$ runs over the points of
$0$ runs over the points of ![]() $D$ and where
$D$ and where ![]() $C$ runs over all smooth locally closed curves of
$C$ runs over all smooth locally closed curves of ![]() $X$ meeting
$X$ meeting ![]() $D$ at
$D$ at ![]() $0$ only.
$0$ only.
2. Cohomological and  $\chi$-boundedness conjectures
$\chi$-boundedness conjectures
2.1 Connections with bounded irregularity
Definition 2.1 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object in
$\mathcal {M}$ be an object in ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. We say that
$D$. We say that ![]() $\mathcal {M}$ has irregularity bounded by
$\mathcal {M}$ has irregularity bounded by ![]() $R$ if the equivalent conditions of Corollary 1.45 are satisfied.
$R$ if the equivalent conditions of Corollary 1.45 are satisfied.
We denote by ![]() $\operatorname {MIC}(X,D,R)$ the full subcategory of
$\operatorname {MIC}(X,D,R)$ the full subcategory of ![]() $\operatorname {MIC}(X,D)$ consisting in connections with irregularity bounded by
$\operatorname {MIC}(X,D)$ consisting in connections with irregularity bounded by ![]() $R$.
$R$.
For an integer ![]() $r\geq 0$, we denote by
$r\geq 0$, we denote by ![]() $\operatorname {MIC}_r(X,D,R)$ the full subcategory of
$\operatorname {MIC}_r(X,D,R)$ the full subcategory of ![]() $\operatorname {MIC}(X,D,R)$ spanned by connections with rank smaller than
$\operatorname {MIC}(X,D,R)$ spanned by connections with rank smaller than ![]() $r$.
$r$.
2.2 Bounded irregularity and  ${\mathcal {H}}\! \operatorname {om}$
${\mathcal {H}}\! \operatorname {om}$
The ![]() ${\mathcal {H}}\! \operatorname {om}$ construction for connections preserves boundedness of irregularity in the following sense.
${\mathcal {H}}\! \operatorname {om}$ construction for connections preserves boundedness of irregularity in the following sense.
Proposition 2.2 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $r\geq 0$ be an integer. Let
$r\geq 0$ be an integer. Let ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ be objects of
$\mathcal {M}_2$ be objects of ![]() $\operatorname {MIC}_r(X,D,R)$. Then,
$\operatorname {MIC}_r(X,D,R)$. Then, ![]() ${\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1,\mathcal {M}_2)$ is an object of
${\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1,\mathcal {M}_2)$ is an object of ![]() $\operatorname {MIC}_{r^2}(X,D,2r^2\cdot R)$.
$\operatorname {MIC}_{r^2}(X,D,2r^2\cdot R)$.
Proof. We can suppose that ![]() $D$ is irreducible with generic point
$D$ is irreducible with generic point ![]() $\eta$. Let
$\eta$. Let ![]() $(\varphi _\alpha,\mathcal {R}_\alpha ), \alpha \in I$ and
$(\varphi _\alpha,\mathcal {R}_\alpha ), \alpha \in I$ and ![]() $(\psi _\beta,\mathcal {S}_{\beta }), \beta \in J$ be the constituents of the good formal structures of
$(\psi _\beta,\mathcal {S}_{\beta }), \beta \in J$ be the constituents of the good formal structures of ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ at
$\mathcal {M}_2$ at ![]() $\eta$ as in (1.27). With the notation from Definition 1.34, we have
$\eta$ as in (1.27). With the notation from Definition 1.34, we have
Since ![]() $(\operatorname {ord}_y \psi _\beta -\varphi _\alpha )\leq (\operatorname {ord}_y \varphi _\alpha )+(\operatorname {ord}_y \psi _\beta )$, we deduce
$(\operatorname {ord}_y \psi _\beta -\varphi _\alpha )\leq (\operatorname {ord}_y \varphi _\alpha )+(\operatorname {ord}_y \psi _\beta )$, we deduce
 \begin{align*} \operatorname{irr}(D,{\mathcal{H}}\! \operatorname{om}(\mathcal{M}_1,\mathcal{M}_2)) & \leq |J|\operatorname{rk} \mathcal{M}_2\sum_{I } (\operatorname{ord}_y \varphi_\alpha )\cdot (\operatorname{rk} \mathcal{R}_\alpha)+|I|\operatorname{rk} \mathcal{M}_1 \sum_{ J} (\operatorname{ord}_y \psi_\beta )\cdot (\operatorname{rk} \mathcal{S}_\beta)\\ & \leq (\operatorname{rk}\mathcal{M}_2)^2 \cdot \operatorname{irr}(D,\mathcal{M}_1) +(\operatorname{rk}\mathcal{M}_1)^2 \cdot \operatorname{irr}(D,\mathcal{M}_2). \end{align*}
\begin{align*} \operatorname{irr}(D,{\mathcal{H}}\! \operatorname{om}(\mathcal{M}_1,\mathcal{M}_2)) & \leq |J|\operatorname{rk} \mathcal{M}_2\sum_{I } (\operatorname{ord}_y \varphi_\alpha )\cdot (\operatorname{rk} \mathcal{R}_\alpha)+|I|\operatorname{rk} \mathcal{M}_1 \sum_{ J} (\operatorname{ord}_y \psi_\beta )\cdot (\operatorname{rk} \mathcal{S}_\beta)\\ & \leq (\operatorname{rk}\mathcal{M}_2)^2 \cdot \operatorname{irr}(D,\mathcal{M}_1) +(\operatorname{rk}\mathcal{M}_1)^2 \cdot \operatorname{irr}(D,\mathcal{M}_2). \end{align*}
The proof of Proposition 2.2 thus follows.
2.3 Bounded irregularity and pull-back
Bounded irregularity behaves well with respect to inverse image.
Proposition 2.3 Let ![]() $f: (Y,E)\to (X,D)$ be a morphism of normal crossing pairs over
$f: (Y,E)\to (X,D)$ be a morphism of normal crossing pairs over ![]() $k$. Let
$k$. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Then, for every object
$D$. Then, for every object ![]() $\mathcal {M}$ in
$\mathcal {M}$ in ![]() $\operatorname {MIC}(X,D,R)$, the connection
$\operatorname {MIC}(X,D,R)$, the connection ![]() $f^+\mathcal {M}$ has irregularity bounded by
$f^+\mathcal {M}$ has irregularity bounded by ![]() $f^*R$.
$f^*R$.
Proof. By writing ![]() $f$ as a composition of a closed immersion followed by a smooth morphism, we are left to suppose that
$f$ as a composition of a closed immersion followed by a smooth morphism, we are left to suppose that ![]() $f$ is either a closed immersion or a smooth morphism. In both cases, the sought-after bound is local around the maximal points of
$f$ is either a closed immersion or a smooth morphism. In both cases, the sought-after bound is local around the maximal points of ![]() $E$, so we can suppose in each case that
$E$, so we can suppose in each case that ![]() $E$ is smooth and irreducible.
$E$ is smooth and irreducible.
Let us assume that ![]() $f$ is a smooth morphism. Then, the pull-back
$f$ is a smooth morphism. Then, the pull-back ![]() $E\to D$ is smooth. Since
$E\to D$ is smooth. Since ![]() $E$ is smooth, so is the open set
$E$ is smooth, so is the open set ![]() $f(E)$ of
$f(E)$ of ![]() $D$. Thus,
$D$. Thus, ![]() $f(E)$ lies in a unique irreducible component
$f(E)$ lies in a unique irreducible component ![]() $T$ of
$T$ of ![]() $D$. Since
$D$. Since ![]() $f$ is smooth, so is the pull-back
$f$ is smooth, so is the pull-back ![]() $E\to T$. Hence, the generic point
$E\to T$. Hence, the generic point ![]() $\eta _E$ of
$\eta _E$ of ![]() $E$ lies above the generic point
$E$ lies above the generic point ![]() $\eta _T$ of
$\eta _T$ of ![]() $T$ and a uniformizer of
$T$ and a uniformizer of ![]() $\mathcal {O}_{X,\eta _T}$ pulls back to a uniformizer of
$\mathcal {O}_{X,\eta _T}$ pulls back to a uniformizer of ![]() $\mathcal {O}_{Y,\eta _E}$. Thus, the irregularity numbers of
$\mathcal {O}_{Y,\eta _E}$. Thus, the irregularity numbers of ![]() $\mathcal {M}|_{\eta _T}$ and
$\mathcal {M}|_{\eta _T}$ and ![]() $(f^+\mathcal {M})|_{\eta _E}$ are equal. Hence,
$(f^+\mathcal {M})|_{\eta _E}$ are equal. Hence, ![]() $\operatorname {Irr}(Y,f^+\mathcal {M})=f^*\operatorname {Irr}(X,\mathcal {M})$ and Proposition 2.3 is proved if
$\operatorname {Irr}(Y,f^+\mathcal {M})=f^*\operatorname {Irr}(X,\mathcal {M})$ and Proposition 2.3 is proved if ![]() $f$ is smooth.
$f$ is smooth.
We now assume that ![]() $f$ is a closed immersion with
$f$ is a closed immersion with ![]() $E$ smooth and irreducible. Let
$E$ smooth and irreducible. Let ![]() $0$ be a point in
$0$ be a point in ![]() $E$ and let
$E$ and let ![]() $C\to Y$ be a locally closed smooth curve of
$C\to Y$ be a locally closed smooth curve of ![]() $Y$ meeting
$Y$ meeting ![]() $E$ at
$E$ at ![]() $0$ only. Corollary 1.45 applied to
$0$ only. Corollary 1.45 applied to ![]() $f(C)$ and
$f(C)$ and ![]() $\mathcal {M}$ on
$\mathcal {M}$ on ![]() $X$ gives
$X$ gives
where the last equality follows from the projection formula. Hence, condition (ii) of Corollary 1.45 is satisfied and Proposition 2.3 follows.
2.4 Bounded irregularity and change of compactification I
Bounded irregularity behaves well with respect to compactification by normal crossing pairs.
Proposition 2.4 Let ![]() $U$ be a smooth variety over
$U$ be a smooth variety over ![]() $k$. Let
$k$. Let ![]() $(X_1,D_1)$ and
$(X_1,D_1)$ and ![]() $(X_2,D_2)$ be proper normal crossing pairs over
$(X_2,D_2)$ be proper normal crossing pairs over ![]() $k$ compactifying
$k$ compactifying ![]() $U$, that is
$U$, that is ![]() $U=X_1\setminus D_1=X_2\setminus D_2$. Let
$U=X_1\setminus D_1=X_2\setminus D_2$. Let ![]() $j_1 : U\to X_1$ and
$j_1 : U\to X_1$ and ![]() $j_2 : U\to X_2$ be the inclusions. Let
$j_2 : U\to X_2$ be the inclusions. Let ![]() $R_1$ be an effective divisor of
$R_1$ be an effective divisor of ![]() $X_1$ supported on
$X_1$ supported on ![]() $D_1$. Then, there exists an effective divisor
$D_1$. Then, there exists an effective divisor ![]() $R_2$ of
$R_2$ of ![]() $X_2$ supported on
$X_2$ supported on ![]() $D_2$ depending only on
$D_2$ depending only on ![]() $(X_1,D_1)$,
$(X_1,D_1)$, ![]() $(X_2,D_2)$ and linearly on
$(X_2,D_2)$ and linearly on ![]() $R_1$ such that for every object
$R_1$ such that for every object ![]() $\mathcal {M}_1$ of
$\mathcal {M}_1$ of ![]() $\operatorname {MIC}(X_1,D_1,R_1)$, the connection
$\operatorname {MIC}(X_1,D_1,R_1)$, the connection ![]() $j_{2*}j_1^*\mathcal {M}_1$ lies in
$j_{2*}j_1^*\mathcal {M}_1$ lies in ![]() $\operatorname {MIC}(X_2,D_2,R_2)$.
$\operatorname {MIC}(X_2,D_2,R_2)$.
Proof. Using resolution of singularities, we construct a pair ![]() $(X_3,D_3)$ dominating
$(X_3,D_3)$ dominating ![]() $(X_1,D_1)$ and
$(X_1,D_1)$ and ![]() $(X_2,D_2)$ such that
$(X_2,D_2)$ such that ![]() $D_3$ has normal crossing. That is, there is a commutative diagram
$D_3$ has normal crossing. That is, there is a commutative diagram

with modifications as horizontal arrows where ![]() $D_3$ lies over
$D_3$ lies over ![]() $D_1$ and
$D_1$ and ![]() $D_2$. Let
$D_2$. Let ![]() $\mathcal {M}_1\in \operatorname {MIC}(X_1,D_1,R_1)$. Put
$\mathcal {M}_1\in \operatorname {MIC}(X_1,D_1,R_1)$. Put ![]() $\mathcal {M}_2=j_{2*}j_1^*\mathcal {M}_1$ and
$\mathcal {M}_2=j_{2*}j_1^*\mathcal {M}_1$ and ![]() $\mathcal {M}_3=j_{3*}j_1^*\mathcal {M}_1$. From Proposition 1.23, we have
$\mathcal {M}_3=j_{3*}j_1^*\mathcal {M}_1$. From Proposition 1.23, we have
Let ![]() $E$ be an irreducible component of
$E$ be an irreducible component of ![]() $D_2$. We have to bound
$D_2$. We have to bound ![]() $\operatorname {irr}(E,\mathcal {M}_2)$ by means of
$\operatorname {irr}(E,\mathcal {M}_2)$ by means of ![]() $(X_i,D_i)$,
$(X_i,D_i)$, ![]() $i=1,2$ and
$i=1,2$ and ![]() $R_1$ only. Let
$R_1$ only. Let ![]() $E'$ be the strict transform of
$E'$ be the strict transform of ![]() $E$ in
$E$ in ![]() $X_3$. Then,
$X_3$. Then,
From Theorem 1.44, we further have
We deduce
Hence, ![]() $R_2=p_{2 \ast } p_1^* R_1$ depends linearly on
$R_2=p_{2 \ast } p_1^* R_1$ depends linearly on ![]() $R_1$ and satisfies the condition of Proposition 2.4.
$R_1$ and satisfies the condition of Proposition 2.4.
2.5 Cohomological boundedness conjecture
Recall that if ![]() $G$ is an abelian group and
$G$ is an abelian group and ![]() $d\geq 0$ an integer, a polynomial
$d\geq 0$ an integer, a polynomial ![]() $C : G\to \mathbb {Z}$ of degree at most
$C : G\to \mathbb {Z}$ of degree at most ![]() $d$ is an element of
$d$ is an element of ![]() $\operatorname {Sym}^{\bullet }_{\mathbb {Z}}(G^{\vee })$ of degree at most
$\operatorname {Sym}^{\bullet }_{\mathbb {Z}}(G^{\vee })$ of degree at most ![]() $d$, where
$d$, where ![]() $G^{\vee }$ is the abelian group dual to
$G^{\vee }$ is the abelian group dual to ![]() $G$.
$G$.
Conjecture 2.5 Let ![]() $(X,D)$ be a projective normal crossing pair of dimension
$(X,D)$ be a projective normal crossing pair of dimension ![]() $d$ over
$d$ over ![]() $k$. There exists a polynomial
$k$. There exists a polynomial ![]() $C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree at most
$C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree at most ![]() $d$, affine in the last variable such that for every effective divisor
$d$, affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
Remark 2.6 If a polynomial ![]() $C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ as above exists, we say that cohomological boundedness holds for
$C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ as above exists, we say that cohomological boundedness holds for ![]() $(X,D)$ with bound
$(X,D)$ with bound ![]() $C$.
$C$.
Remark 2.7 Let ![]() $d\geq 0$ be an integer. Let
$d\geq 0$ be an integer. Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $0$. We say that cohomological boundedness holds in dimension
$0$. We say that cohomological boundedness holds in dimension ![]() $d$ over
$d$ over ![]() $k$ if it holds for every choice of
$k$ if it holds for every choice of ![]() $(X,D)$ as above with
$(X,D)$ as above with ![]() $(X,D)$ defined over
$(X,D)$ defined over ![]() $k$ and
$k$ and ![]() $\dim X=d$.
$\dim X=d$.
Remark 2.8 Let ![]() $d\geq 0$ be an integer. We say that cohomological boundedness holds in dimension
$d\geq 0$ be an integer. We say that cohomological boundedness holds in dimension ![]() $d$ if it holds in dimension
$d$ if it holds in dimension ![]() $d$ over every field of characteristic
$d$ over every field of characteristic ![]() $0$.
$0$.
Lemma 2.9 Cohomological boundedness holds in dimension ![]() $1$.
$1$.
Proof. From Lemma A.1, it is enough to treat the case of a smooth connected projective curve ![]() $X$ of genus
$X$ of genus ![]() $g$ over
$g$ over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $D$ be a reduced divisor of
$D$ be a reduced divisor of ![]() $X$. Let
$X$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. From Proposition 1.9 and Theorem 1.14, we are left to bound the cohomology of
$\operatorname {MIC}(X,D)$. From Proposition 1.9 and Theorem 1.14, we are left to bound the cohomology of ![]() $\operatorname {Sol}(\mathcal {M}^{\operatorname {an}})$. Let
$\operatorname {Sol}(\mathcal {M}^{\operatorname {an}})$. Let ![]() $j : U=X\setminus D \to X$ be the open immersion and put
$j : U=X\setminus D \to X$ be the open immersion and put ![]() $\mathcal {L} :=\operatorname {Sol}(\mathcal {M}^{\operatorname {an}})|_{U(\mathbb {C})}$. Observe that
$\mathcal {L} :=\operatorname {Sol}(\mathcal {M}^{\operatorname {an}})|_{U(\mathbb {C})}$. Observe that ![]() $\mathcal {L}$ is a local system of rank
$\mathcal {L}$ is a local system of rank ![]() $\operatorname {rk} \mathcal {M}$ on
$\operatorname {rk} \mathcal {M}$ on ![]() $U(\mathbb {C})$. From Lemma 1.36, there is the following distinguished triangle.
$U(\mathbb {C})$. From Lemma 1.36, there is the following distinguished triangle.
We have ![]() $H^{0}(X(\mathbb {C}), j_!\mathcal {L} )\simeq 0$. If
$H^{0}(X(\mathbb {C}), j_!\mathcal {L} )\simeq 0$. If ![]() $\mathcal {L}^*$ denotes the dual of
$\mathcal {L}^*$ denotes the dual of ![]() $\mathcal {L}$, Poincaré duality further gives
$\mathcal {L}$, Poincaré duality further gives
On the other hand, ![]() $\chi _c(U(\mathbb {C}), \mathcal {L} )=\operatorname {rk} \mathcal {M} \cdot \chi (U(\mathbb {C}), \mathbb {C} )=\operatorname {rk} \mathcal {M} \cdot (2-2g-|D|)$. Then, Lemma 2.9 follows from the long exact sequence in cohomology induced by the above distinguished triangle.
$\chi _c(U(\mathbb {C}), \mathcal {L} )=\operatorname {rk} \mathcal {M} \cdot \chi (U(\mathbb {C}), \mathbb {C} )=\operatorname {rk} \mathcal {M} \cdot (2-2g-|D|)$. Then, Lemma 2.9 follows from the long exact sequence in cohomology induced by the above distinguished triangle.
2.6 The  $\chi$-boundedness conjecture
$\chi$-boundedness conjecture
We formulate an a priori weaker version of the cohomological boundedness conjecture.
Conjecture 2.10 Let ![]() $(X,D)$ be a projective normal crossing pair of dimension
$(X,D)$ be a projective normal crossing pair of dimension ![]() $d$ over
$d$ over ![]() $k$. There exists a polynomial
$k$. There exists a polynomial ![]() $C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree at most
$C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree at most ![]() $d$, affine in the last variable such that for every effective divisor
$d$, affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
Remark 2.11 We adopt for the ![]() $\chi$-boundedness conjecture the terminology from Remarks 2.6–2.8 for the cohomological boundedness conjecture.
$\chi$-boundedness conjecture the terminology from Remarks 2.6–2.8 for the cohomological boundedness conjecture.
Remark 2.12 Let ![]() $d\geq 0$ be an integer. Similarly as in Lemma A.1, the
$d\geq 0$ be an integer. Similarly as in Lemma A.1, the ![]() $\chi$-boundedness conjecture holds in dimension
$\chi$-boundedness conjecture holds in dimension ![]() $d$ if it holds in dimension
$d$ if it holds in dimension ![]() $d$ over
$d$ over ![]() $\mathbb {C}$.
$\mathbb {C}$.
Cohomological boundedness trivially implies ![]() $\chi$-boundedness. The goal of the next subsection is to show that they are equivalent.
$\chi$-boundedness. The goal of the next subsection is to show that they are equivalent.
2.7 The cohomological and  $\chi$-boundedness conjectures are equivalent
$\chi$-boundedness conjectures are equivalent
Proposition 2.13 Let ![]() $\mathbb {P}$ be a projective space over
$\mathbb {P}$ be a projective space over ![]() $k$. Let
$k$. Let ![]() $X$ be a smooth subvariety of
$X$ be a smooth subvariety of ![]() $\mathbb {P}$. Let
$\mathbb {P}$. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Let
$\mathcal {D}_X$-module. Let ![]() $H\in \mathbb {P}^{\vee }(k)$ be a hyperplane such that
$H\in \mathbb {P}^{\vee }(k)$ be a hyperplane such that ![]() $X\cap H$ is smooth and
$X\cap H$ is smooth and ![]() $X\cap H \to X$ is non-characteristic for
$X\cap H \to X$ is non-characteristic for ![]() $\mathcal {M}$. Then the canonical comparison morphism
$\mathcal {M}$. Then the canonical comparison morphism
is an isomorphism if ![]() $n<\dim X-1$ and is injective if
$n<\dim X-1$ and is injective if ![]() $n=\dim X-1$.
$n=\dim X-1$.
Proof. From Remark 1.11, we reduce to the case where ![]() $k=\mathbb {C}$. From Proposition 1.9, we are left to prove a variant of Proposition 2.13 where now
$k=\mathbb {C}$. From Proposition 1.9, we are left to prove a variant of Proposition 2.13 where now ![]() $X$ is the analytification of a smooth complex algebraic variety and where
$X$ is the analytification of a smooth complex algebraic variety and where ![]() $\mathcal {M}$ is the analytification of a holonomic
$\mathcal {M}$ is the analytification of a holonomic ![]() $\mathcal {D}$-module. Then Theorem 1.12 ensures that
$\mathcal {D}$-module. Then Theorem 1.12 ensures that ![]() $\operatorname {DR} \mathcal {M}[\dim X]$ is a perverse complex. From the Lefschetz hyperplane theorem for perverse complexes [Reference de CataldodCat17, 2.4.2], the canonical comparison morphism
$\operatorname {DR} \mathcal {M}[\dim X]$ is a perverse complex. From the Lefschetz hyperplane theorem for perverse complexes [Reference de CataldodCat17, 2.4.2], the canonical comparison morphism
is an isomorphism if ![]() $n<\dim X-1$ and is injective if
$n<\dim X-1$ and is injective if ![]() $n=\dim X-1$. Since
$n=\dim X-1$. Since ![]() $X\cap H \to X$ is non-characteristic for
$X\cap H \to X$ is non-characteristic for ![]() $\mathcal {M}$, we conclude the proof of Proposition 2.13 using Theorem 1.20.
$\mathcal {M}$, we conclude the proof of Proposition 2.13 using Theorem 1.20.
Remark 2.14 When ![]() $X$ is a projective complex manifold, Proposition 2.13 is also valid via the same reasoning with either the analytic de Rham complex or the solution complex.
$X$ is a projective complex manifold, Proposition 2.13 is also valid via the same reasoning with either the analytic de Rham complex or the solution complex.
Corollary 2.15 In the setting of Proposition 2.13, assume the existence of ![]() $C\geq 0$ with
$C\geq 0$ with
Then, if ![]() $d$ denotes the dimension of
$d$ denotes the dimension of ![]() $X$, we have
$X$, we have
Proof. We can suppose that ![]() $k=\mathbb {C}$. From Proposition 2.13, we have for
$k=\mathbb {C}$. From Proposition 2.13, we have for ![]() $n< d$,
$n< d$,
Assume that ![]() $n>d$. Then,
$n>d$. Then,
 \begin{align*} \dim H^{n}(X,\operatorname{DR} \mathcal{M}) &= \dim H^{n}(X(\mathbb{C}),\operatorname{DR} \mathcal{M}^{\operatorname{an}}) \\ & =\dim H^{2d-n}(X(\mathbb{C}),\operatorname{Sol} \mathcal{M}^{\operatorname{an}})\\ & \leq \dim H^{2d-n}((X\cap H)(\mathbb{C}),\operatorname{Sol} (\mathcal{M}^{\operatorname{an}}|_{(X\cap H)(\mathbb{C})}))\\ & \leq \dim H^{n-2}((X\cap H)(\mathbb{C}),\operatorname{DR}(\mathcal{M}^{\operatorname{an}}|_{(X\cap H)(\mathbb{C})})) \\ & \leq \dim H^{n-2}(X\cap H,\operatorname{DR}(\mathcal{M}|_{X\cap H})) \leq C, \end{align*}
\begin{align*} \dim H^{n}(X,\operatorname{DR} \mathcal{M}) &= \dim H^{n}(X(\mathbb{C}),\operatorname{DR} \mathcal{M}^{\operatorname{an}}) \\ & =\dim H^{2d-n}(X(\mathbb{C}),\operatorname{Sol} \mathcal{M}^{\operatorname{an}})\\ & \leq \dim H^{2d-n}((X\cap H)(\mathbb{C}),\operatorname{Sol} (\mathcal{M}^{\operatorname{an}}|_{(X\cap H)(\mathbb{C})}))\\ & \leq \dim H^{n-2}((X\cap H)(\mathbb{C}),\operatorname{DR}(\mathcal{M}^{\operatorname{an}}|_{(X\cap H)(\mathbb{C})})) \\ & \leq \dim H^{n-2}(X\cap H,\operatorname{DR}(\mathcal{M}|_{X\cap H})) \leq C, \end{align*}
where the first and fifth inequality follow from Proposition 1.9, the second follows from Theorem 1.14 and Poincaré–Verdier duality on ![]() $X(\mathbb {C})$, the third follows from Remark 2.14 since
$X(\mathbb {C})$, the third follows from Remark 2.14 since ![]() $2d-n< d$ and the fourth inequality follows from Theorem 1.14 and Poincaré–Verdier duality on
$2d-n< d$ and the fourth inequality follows from Theorem 1.14 and Poincaré–Verdier duality on ![]() $(X\cap H)(\mathbb {C})$. Furthermore, Proposition 1.10 yields
$(X\cap H)(\mathbb {C})$. Furthermore, Proposition 1.10 yields
 \begin{align*} \dim H^{d}(X,\operatorname{DR} \mathcal{M})& \leq |\chi(X,\operatorname{DR} \mathcal{M})| + \displaystyle{\sum_{n\neq d}} \dim H^{n}(X,\operatorname{DR} \mathcal{M})\\ & \leq |\chi(X,\operatorname{DR} \mathcal{M})| + 2d \cdot C. \end{align*}
\begin{align*} \dim H^{d}(X,\operatorname{DR} \mathcal{M})& \leq |\chi(X,\operatorname{DR} \mathcal{M})| + \displaystyle{\sum_{n\neq d}} \dim H^{n}(X,\operatorname{DR} \mathcal{M})\\ & \leq |\chi(X,\operatorname{DR} \mathcal{M})| + 2d \cdot C. \end{align*}
Putting all the above inequalities together finishes the proof of Corollary 2.15.
Proposition 2.16 Let ![]() $(X,D)$ be a projective normal crossing pair of dimension
$(X,D)$ be a projective normal crossing pair of dimension ![]() $d$ over
$d$ over ![]() $k$. Let
$k$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Assume that
$X\to \mathbb {P}$ be a closed immersion in some projective space. Assume that ![]() $\chi$-boundedness holds for
$\chi$-boundedness holds for ![]() $(X,D)$ with bound
$(X,D)$ with bound ![]() $K$ and that cohomological boundedness holds with bound
$K$ and that cohomological boundedness holds with bound ![]() $C$ for the generic hyperplane section
$C$ for the generic hyperplane section ![]() $(X_\eta,D_\eta )$ of
$(X_\eta,D_\eta )$ of ![]() $(X,D)$. Then, cohomological boundedness holds for
$(X,D)$. Then, cohomological boundedness holds for ![]() $(X,D)$ with bound
$(X,D)$ with bound ![]() $K+4d\cdot C'$ where
$K+4d\cdot C'$ where ![]() $C'$ is the composition of
$C'$ is the composition of ![]() $C$ with the linear map
$C$ with the linear map ![]() $\operatorname {Div}(X,D)\oplus \mathbb {Z}\to \operatorname {Div}(X_\eta,D_\eta )\oplus \mathbb {Z}$ deduced from
$\operatorname {Div}(X,D)\oplus \mathbb {Z}\to \operatorname {Div}(X_\eta,D_\eta )\oplus \mathbb {Z}$ deduced from ![]() $X_\eta \to X$.
$X_\eta \to X$.
Proof. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $r$ be an integer. By Bertini's theorem, there exists a dense open subset
$r$ be an integer. By Bertini's theorem, there exists a dense open subset ![]() $V$ in
$V$ in ![]() $\mathbb {P}^{\vee }$ such that for every hyperplane
$\mathbb {P}^{\vee }$ such that for every hyperplane ![]() $H\in V(k)$, the pair
$H\in V(k)$, the pair ![]() $(X\cap H, D\cap H)$ is smooth of dimension
$(X\cap H, D\cap H)$ is smooth of dimension ![]() $d-1$ and
$d-1$ and ![]() $D\cap H$ has normal crossing. Let
$D\cap H$ has normal crossing. Let ![]() $\eta$ be the generic point of
$\eta$ be the generic point of ![]() $\mathbb {P}^{\vee }$. Following the notation from § 1.4, consider the following commutative diagram with cartesian squares.
$\mathbb {P}^{\vee }$. Following the notation from § 1.4, consider the following commutative diagram with cartesian squares.

Let ![]() $\pi : X_Q\to \mathbb {P}^{\vee }$ be the composition morphism and let
$\pi : X_Q\to \mathbb {P}^{\vee }$ be the composition morphism and let ![]() $\pi _V : X_V\to V$ and
$\pi _V : X_V\to V$ and ![]() $\pi _{\eta } : X_{\eta }\to \eta$ be its pull-back above
$\pi _{\eta } : X_{\eta }\to \eta$ be its pull-back above ![]() $V$ and
$V$ and ![]() $\eta$, respectively. Let
$\eta$, respectively. Let ![]() $D_V$ and
$D_V$ and ![]() $R_V$ be the pull-back of
$R_V$ be the pull-back of ![]() $D$ and
$D$ and ![]() $R$ to
$R$ to ![]() $X_V$ and let
$X_V$ and let ![]() $D_\eta$ and
$D_\eta$ and ![]() $R_\eta$ be their pull-back to
$R_\eta$ be their pull-back to ![]() $X_\eta$. Observe that
$X_\eta$. Observe that ![]() $(X_\eta,D_\eta )$ is a pair of dimension
$(X_\eta,D_\eta )$ is a pair of dimension ![]() $d-1$ over
$d-1$ over ![]() $\eta$ where
$\eta$ where ![]() $D_{\eta }$ has normal crossing. Since cohomological boundedness holds for
$D_{\eta }$ has normal crossing. Since cohomological boundedness holds for ![]() $(X_\eta,D_\eta )$ with bound
$(X_\eta,D_\eta )$ with bound ![]() $C$, we have for every object
$C$, we have for every object ![]() $\mathcal {N}_\eta$ in
$\mathcal {N}_\eta$ in ![]() $\operatorname {MIC}_r(X_\eta,D_\eta,R_\eta )$,
$\operatorname {MIC}_r(X_\eta,D_\eta,R_\eta )$,
On the other hand, for every object ![]() $\mathcal {N}$ in
$\mathcal {N}$ in ![]() $\operatorname {MIC}_r(X_V,D_V ,R_V)$ we have
$\operatorname {MIC}_r(X_V,D_V ,R_V)$ we have
Thus, the space ![]() $H^n(X_\eta,\operatorname {DR} \mathcal {N}_\eta )$ is the generic fibre of the
$H^n(X_\eta,\operatorname {DR} \mathcal {N}_\eta )$ is the generic fibre of the ![]() $\mathcal {D}_V$-module
$\mathcal {D}_V$-module
for every ![]() $n\geq 0$. Let
$n\geq 0$. Let ![]() $\mathcal {M}$ be an object in
$\mathcal {M}$ be an object in ![]() $\operatorname {MIC}_r(X,D,R)$. From Proposition 2.3, the pull-back
$\operatorname {MIC}_r(X,D,R)$. From Proposition 2.3, the pull-back ![]() $\mathcal {M}_V$ of
$\mathcal {M}_V$ of ![]() $\mathcal {M}$ to
$\mathcal {M}$ to ![]() $X_V$ lies in
$X_V$ lies in ![]() $\operatorname {MIC}_r(X_V,D_V ,R_V)$. Since
$\operatorname {MIC}_r(X_V,D_V ,R_V)$. Since ![]() $k$ is infinite, Lemma 1.5 ensures the existence of a hyperplane
$k$ is infinite, Lemma 1.5 ensures the existence of a hyperplane ![]() $H\in V(k)$ such that
$H\in V(k)$ such that ![]() $X\cap H\to X$ is non-characteristic for
$X\cap H\to X$ is non-characteristic for ![]() $\mathcal {M}$ and such that the cohomology modules of
$\mathcal {M}$ and such that the cohomology modules of ![]() $\pi _{V+}\mathcal {M}_V$ are flat connections in a neighbourhood of
$\pi _{V+}\mathcal {M}_V$ are flat connections in a neighbourhood of ![]() $H\in V(k)$. In particular, the inclusion
$H\in V(k)$. In particular, the inclusion ![]() $i : \{H\} \to V$ is non-characteristic for the cohomology modules of
$i : \{H\} \to V$ is non-characteristic for the cohomology modules of ![]() $\pi _{V+}\mathcal {M}_V$. Hence, Theorem 1.20 combined with base change for
$\pi _{V+}\mathcal {M}_V$. Hence, Theorem 1.20 combined with base change for ![]() $\mathcal {D}$-modules [Reference Hotta, Takeuchi and TanisakiHTT00, 1.7.3] yields
$\mathcal {D}$-modules [Reference Hotta, Takeuchi and TanisakiHTT00, 1.7.3] yields
 \begin{align*} i^*\mathcal{H}^{n-d+1} \pi _{V+}\mathcal{M}_V & \simeq \mathcal{H}^{n-d+1} i^+ \pi _{V+}\mathcal{M}_V \\ & \simeq \mathcal{H}^n \pi _{H+}(\mathcal{M}_V|_{X\cap H}) \\ & \simeq H^n(X\cap H, \operatorname{DR}\mathcal{M}|_{X\cap H} ), \end{align*}
\begin{align*} i^*\mathcal{H}^{n-d+1} \pi _{V+}\mathcal{M}_V & \simeq \mathcal{H}^{n-d+1} i^+ \pi _{V+}\mathcal{M}_V \\ & \simeq \mathcal{H}^n \pi _{H+}(\mathcal{M}_V|_{X\cap H}) \\ & \simeq H^n(X\cap H, \operatorname{DR}\mathcal{M}|_{X\cap H} ), \end{align*}
where ![]() $\pi _{H} : X\cap H \to \{H\}$ is the pull-back of
$\pi _{H} : X\cap H \to \{H\}$ is the pull-back of ![]() $\pi$ above
$\pi$ above ![]() $H\in V(k)$. Since
$H\in V(k)$. Since ![]() $\mathcal {H}^{n-d+1} \pi _{V+}\mathcal {M}_V$ is a flat connection in a neighbourhood of
$\mathcal {H}^{n-d+1} \pi _{V+}\mathcal {M}_V$ is a flat connection in a neighbourhood of ![]() $H$, we also have
$H$, we also have
Thus,
Then, Corollary 2.15 yields
which concludes the proof of Proposition 2.16.
Corollary 2.17 Let ![]() $d\geq 2$ be an integer. Then cohomological boundedness holds in dimension
$d\geq 2$ be an integer. Then cohomological boundedness holds in dimension ![]() $d$ if it holds in dimension
$d$ if it holds in dimension ![]() $d-1$ and if
$d-1$ and if ![]() $\chi$-boundedness holds in dimension
$\chi$-boundedness holds in dimension ![]() $d$.
$d$.
From Lemma 2.9 and Corollary 2.17, we deduce the following.
Corollary 2.18 The cohomological and ![]() $\chi$-boundedness conjectures are equivalent.
$\chi$-boundedness conjectures are equivalent.
3. Nearby slopes and boundedness
3.1 Resolution relative to a normal crossing divisor
Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. If
$k$. If ![]() $C$ is a closed subscheme of
$C$ is a closed subscheme of ![]() $X$, we say that
$X$, we say that ![]() $C$ and
$C$ and ![]() $D$ have simultaneously only normal crossing if for every point
$D$ have simultaneously only normal crossing if for every point ![]() $x$ of
$x$ of ![]() $C$, there exists a regular system of parameters
$C$, there exists a regular system of parameters ![]() $(x_1,\ldots, x_n)$ for
$(x_1,\ldots, x_n)$ for ![]() $\mathcal {O}_{X,x}$ such that
$\mathcal {O}_{X,x}$ such that ![]() $\mathcal {I}_{D}$ is generated at
$\mathcal {I}_{D}$ is generated at ![]() $x$ by
$x$ by ![]() $x_1\cdots x_k$ and
$x_1\cdots x_k$ and ![]() $\mathcal {I}_{C}$ is generated at
$\mathcal {I}_{C}$ is generated at ![]() $x$ by some monomials in the
$x$ by some monomials in the ![]() $x_j$ for
$x_j$ for ![]() $j=1,\ldots, n$ (therefore, by some
$j=1,\ldots, n$ (therefore, by some ![]() $x_j$ if
$x_j$ if ![]() $C$ is smooth at
$C$ is smooth at ![]() $x$).
$x$).
Definition 3.1 Let ![]() $Z$ be a closed subscheme of
$Z$ be a closed subscheme of ![]() $X$. We say that a blow-up
$X$. We say that a blow-up ![]() $p : Y\to X$ with centre
$p : Y\to X$ with centre ![]() $C$ is admissible with respect to
$C$ is admissible with respect to ![]() $(Z,D)$ if the following conditions are satisfied:
$(Z,D)$ if the following conditions are satisfied:
(i)
 $C$ is a smooth nowhere dense subset of
$C$ is a smooth nowhere dense subset of  $Z_{\mathrm {red}}$;
$Z_{\mathrm {red}}$;(ii)
 $C$ and
$C$ and  $D$ have simultaneously only normal crossing.
$D$ have simultaneously only normal crossing.
Then, we denote by ![]() $Z'$ the strict transform of
$Z'$ the strict transform of ![]() $Z$ and put
$Z$ and put ![]() $D'=p^{-1}(D)\cup p^{-1}(C)$ endowed with its reduced structure. The pair
$D'=p^{-1}(D)\cup p^{-1}(C)$ endowed with its reduced structure. The pair ![]() $(Z^{\prime },D^{\prime })$ is the transform of
$(Z^{\prime },D^{\prime })$ is the transform of ![]() $(Z,D)$ by
$(Z,D)$ by ![]() $p : Y\to X$.
$p : Y\to X$.
The form of embedded resolution needed in this paper is the following theorem. For a proof, see Theorems 8.4 and 8.6 in [Reference Bierstone and MilmanBM89].
Theorem 3.2 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $Z$ be a closed subscheme of
$Z$ be a closed subscheme of ![]() $X$. Then, there exists a composition
$X$. Then, there exists a composition ![]() $p: Y\to X$ of admissible blow-up with respect to the successive transforms of
$p: Y\to X$ of admissible blow-up with respect to the successive transforms of ![]() $(Z,D)$ such that the final transform
$(Z,D)$ such that the final transform ![]() $(Z',D')$ satisfies that
$(Z',D')$ satisfies that ![]() $Z'_{\mathrm {red}}$ is smooth and
$Z'_{\mathrm {red}}$ is smooth and ![]() $(Z',D')$ have simultaneously only normal crossing.
$(Z',D')$ have simultaneously only normal crossing.
Definition 3.3 A map ![]() $p: Y\to X$ as above is a resolution of
$p: Y\to X$ as above is a resolution of ![]() $Z$ relative to
$Z$ relative to ![]() $D$.
$D$.
The following lemma is obvious from the definitions.
Lemma 3.4 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $Z,T$ be subschemes of
$Z,T$ be subschemes of ![]() $X$ with
$X$ with ![]() $T_{\mathrm {red}}\subset Z_{\mathrm {red}}$. Then a blow-up of
$T_{\mathrm {red}}\subset Z_{\mathrm {red}}$. Then a blow-up of ![]() $X$ admissible with respect to
$X$ admissible with respect to ![]() $(T,D)$ is admissible with respect to
$(T,D)$ is admissible with respect to ![]() $(Z,D)$.
$(Z,D)$.
Lemma 3.5 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $Z,T$ be subschemes of
$Z,T$ be subschemes of ![]() $X$ with
$X$ with ![]() $T_{\mathrm {red}}\subset Z_{\mathrm {red}}$ such that
$T_{\mathrm {red}}\subset Z_{\mathrm {red}}$ such that ![]() $T_{\mathrm {red}}$ is nowhere dense in
$T_{\mathrm {red}}$ is nowhere dense in ![]() $Z_{\mathrm {red}}$. Then, there exists a resolution
$Z_{\mathrm {red}}$. Then, there exists a resolution ![]() $p : Y\to X$ of
$p : Y\to X$ of ![]() $Z$ relative to
$Z$ relative to ![]() $D$ such that the pull-back scheme
$D$ such that the pull-back scheme ![]() $p^{-1}(T)$ is an effective Cartier divisor such that
$p^{-1}(T)$ is an effective Cartier divisor such that ![]() $p^{-1}(T)+D'$ has normal crossings, where
$p^{-1}(T)+D'$ has normal crossings, where ![]() $(Z',D')$ is the transform of
$(Z',D')$ is the transform of ![]() $(Z,D)$ by
$(Z,D)$ by ![]() $p : Y\to X$.
$p : Y\to X$.
Proof. Let ![]() $q : X'\to X$ be a blow-up admissible with respect to
$q : X'\to X$ be a blow-up admissible with respect to ![]() $(T,D)$. From Lemma 3.4, the map
$(T,D)$. From Lemma 3.4, the map ![]() $q$ is admissible with respect to
$q$ is admissible with respect to ![]() $(Z,D)$. Let
$(Z,D)$. Let ![]() $(Z',T',D')$ be the transform of
$(Z',T',D')$ be the transform of ![]() $(Z,T,D)$ by
$(Z,T,D)$ by ![]() $q$. Observe that
$q$. Observe that ![]() $T'_{\mathrm {red}}\subset Z'_{\mathrm {red}}$ and that
$T'_{\mathrm {red}}\subset Z'_{\mathrm {red}}$ and that ![]() $T'_{\mathrm {red}}$ is nowhere dense in
$T'_{\mathrm {red}}$ is nowhere dense in ![]() $Z'_{\mathrm {red}}$. We argue that if Lemma 3.5 holds for
$Z'_{\mathrm {red}}$. We argue that if Lemma 3.5 holds for ![]() $(X',D',Z',T')$, then it holds for
$(X',D',Z',T')$, then it holds for ![]() $(X,D,Z,T)$. Indeed, let
$(X,D,Z,T)$. Indeed, let ![]() $\rho : Y'\to X'$ be a resolution of
$\rho : Y'\to X'$ be a resolution of ![]() $Z'$ relative to
$Z'$ relative to ![]() $D'$ such that the pull-back scheme
$D'$ such that the pull-back scheme ![]() $\rho ^{-1}(T')$ is an effective Cartier divisor such that
$\rho ^{-1}(T')$ is an effective Cartier divisor such that ![]() $\rho ^{-1}(T')+D''$ has normal crossing, where
$\rho ^{-1}(T')+D''$ has normal crossing, where ![]() $(Z'',D'')$ is the transform of
$(Z'',D'')$ is the transform of ![]() $(Z',D')$ by
$(Z',D')$ by ![]() $\rho$. Then, the composition
$\rho$. Then, the composition ![]() $\rho \circ q : Y'\to X$ is a resolution of
$\rho \circ q : Y'\to X$ is a resolution of ![]() $Z$ relative to
$Z$ relative to ![]() $D$. On the other hand, we have
$D$. On the other hand, we have ![]() $q^{-1}(T)=T' \cup E$ where
$q^{-1}(T)=T' \cup E$ where ![]() $E$ is an effective Cartier divisor. Thus
$E$ is an effective Cartier divisor. Thus ![]() $\rho ^{-1}(q^{-1}(T))=\rho ^{-1}(T')\cup \rho ^{-1}(E)$ is an effective Cartier divisor. Observe that
$\rho ^{-1}(q^{-1}(T))=\rho ^{-1}(T')\cup \rho ^{-1}(E)$ is an effective Cartier divisor. Observe that ![]() $(Z'',D'')$ is also the transform of
$(Z'',D'')$ is also the transform of ![]() $(Z,D)$ by
$(Z,D)$ by ![]() $\rho \circ q$. Since
$\rho \circ q$. Since ![]() $D''$ contains
$D''$ contains ![]() $\rho ^{-1}(E)$, the divisors
$\rho ^{-1}(E)$, the divisors ![]() $\rho ^{-1}(T')+D''$ and
$\rho ^{-1}(T')+D''$ and ![]() $\rho ^{-1}q^{-1}(T)+D''$ have the same support. Hence,
$\rho ^{-1}q^{-1}(T)+D''$ have the same support. Hence, ![]() $\rho ^{-1}q^{-1}(T)+D''$ has normal crossing and Lemma 3.5 is indeed true for
$\rho ^{-1}q^{-1}(T)+D''$ has normal crossing and Lemma 3.5 is indeed true for ![]() $(X,D,Z,T)$.
$(X,D,Z,T)$.
Using a resolution of ![]() $T$ relative to
$T$ relative to ![]() $D$ as given by Theorem 3.2, we are thus left to prove Lemma 3.5 in the case where
$D$ as given by Theorem 3.2, we are thus left to prove Lemma 3.5 in the case where ![]() $T_{\mathrm {red}}$ is smooth and
$T_{\mathrm {red}}$ is smooth and ![]() $T$ and
$T$ and ![]() $D$ have simultaneously only normal crossings. In particular,
$D$ have simultaneously only normal crossings. In particular, ![]() $T_{\mathrm {red}}$ and
$T_{\mathrm {red}}$ and ![]() $D$ have simultaneously only normal crossings. Let
$D$ have simultaneously only normal crossings. Let ![]() $q : X'\to X$ be the blow-up of
$q : X'\to X$ be the blow-up of ![]() $X$ at
$X$ at ![]() $T_{\mathrm {red}}$. Since
$T_{\mathrm {red}}$. Since ![]() $T_{\mathrm {red}}\subset Z_{\mathrm {red}}$ is nowhere dense in
$T_{\mathrm {red}}\subset Z_{\mathrm {red}}$ is nowhere dense in ![]() $Z_{\mathrm {red}}$, the map
$Z_{\mathrm {red}}$, the map ![]() $q : X'\to X$ is admissible with respect to
$q : X'\to X$ is admissible with respect to ![]() $(Z,D)$. Let
$(Z,D)$. Let ![]() $(Z',D')$ be the transform of
$(Z',D')$ be the transform of ![]() $(Z,D)$ by
$(Z,D)$ by ![]() $q$. Let
$q$. Let ![]() $\rho : Y'\to X'$ be a resolution of
$\rho : Y'\to X'$ be a resolution of ![]() $Z'$ relative to
$Z'$ relative to ![]() $D'$. We claim that the map
$D'$. We claim that the map ![]() $p:=\rho \circ q : Y'\to X$ does the job. Let
$p:=\rho \circ q : Y'\to X$ does the job. Let ![]() $(Z'',D'')$ be the transform of
$(Z'',D'')$ be the transform of ![]() $(Z',D')$ by
$(Z',D')$ by ![]() $\rho$. Then,
$\rho$. Then, ![]() $p : Y'\to X$ is a resolution of
$p : Y'\to X$ is a resolution of ![]() $Z$ relative to
$Z$ relative to ![]() $D$ and
$D$ and ![]() $(Z'',D'')$ is the transform of
$(Z'',D'')$ is the transform of ![]() $(Z,D)$ by
$(Z,D)$ by ![]() $p$. Since
$p$. Since ![]() $q^{-1}(T_{\mathrm {red}})$ is an effective Cartier divisor of
$q^{-1}(T_{\mathrm {red}})$ is an effective Cartier divisor of ![]() $X'$, so is
$X'$, so is ![]() $q^{-1}(T)$. Hence,
$q^{-1}(T)$. Hence, ![]() $p^{-1}(T)$ is an effective Cartier divisor of
$p^{-1}(T)$ is an effective Cartier divisor of ![]() $Y'$. We are thus left to show that
$Y'$. We are thus left to show that ![]() $p^{-1}(T)+D''$ has normal crossings. Observe that
$p^{-1}(T)+D''$ has normal crossings. Observe that ![]() $D''$ contains
$D''$ contains ![]() $\rho ^{-1}(D')$. Since
$\rho ^{-1}(D')$. Since ![]() $D'$ contains
$D'$ contains ![]() $q^{-1}(T)$ by definition,
$q^{-1}(T)$ by definition, ![]() $D''$ contains
$D''$ contains ![]() $p^{-1}(T)$. We are thus left to showing that
$p^{-1}(T)$. We are thus left to showing that ![]() $D''$ has normal crossings, which is obvious by construction.
$D''$ has normal crossings, which is obvious by construction.
3.2 Bounded irregularity and change of compactification II
Proposition 3.7 below provides a generalization of Proposition 2.4 where part of the divisor at infinity is being kept while changing compactification. Before proving it, we need the following.
Lemma 3.6 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$ and let
$k$ and let ![]() $Z$ be a divisor of
$Z$ be a divisor of ![]() $X$. Let
$X$. Let ![]() $p : Y\to X$ be a resolution of
$p : Y\to X$ be a resolution of ![]() $Z$ relative to
$Z$ relative to ![]() $D$ and put
$D$ and put ![]() $F:=(p^{-1}(Z\cup D))_{\mathrm {red}}$. Let
$F:=(p^{-1}(Z\cup D))_{\mathrm {red}}$. Let ![]() $R$ be an effective divisor supported on
$R$ be an effective divisor supported on ![]() $D$. Then for every object
$D$. Then for every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}(X,D,R)$, the connection
$\operatorname {MIC}(X,D,R)$, the connection ![]() $(p^+ \mathcal {M})(\ast F)$ lies in
$(p^+ \mathcal {M})(\ast F)$ lies in ![]() $\operatorname {MIC}(Y,F,p^*R)$.
$\operatorname {MIC}(Y,F,p^*R)$.
Proof. Put ![]() $E=f^{-1}(D)$. By definition of a resolution relative to a normal crossing divisor, the divisors
$E=f^{-1}(D)$. By definition of a resolution relative to a normal crossing divisor, the divisors ![]() $E\subset F$ have normal crossing. In particular,
$E\subset F$ have normal crossing. In particular, ![]() $p : (Y,E)\to (X,D)$ is a morphism of normal crossing pairs. From Proposition 2.3, we deduce that
$p : (Y,E)\to (X,D)$ is a morphism of normal crossing pairs. From Proposition 2.3, we deduce that ![]() $p^+ \mathcal {M}$ is an object of
$p^+ \mathcal {M}$ is an object of ![]() $\operatorname {MIC}(Y,E,p^*R)$. Along a component of
$\operatorname {MIC}(Y,E,p^*R)$. Along a component of ![]() $F$ that is not a component of
$F$ that is not a component of ![]() $E$, the generic irregularity of
$E$, the generic irregularity of ![]() $(p^+ \mathcal {M})(\ast F)$ is
$(p^+ \mathcal {M})(\ast F)$ is ![]() $0$. Thus,
$0$. Thus, ![]() $(p^+ \mathcal {M})(\ast F)$ is an object of
$(p^+ \mathcal {M})(\ast F)$ is an object of ![]() $\operatorname {MIC}(Y,F,p^*R)$ and Lemma 3.6 is proved.
$\operatorname {MIC}(Y,F,p^*R)$ and Lemma 3.6 is proved.
Proposition 3.7 Let ![]() $(X,D)$ be a proper normal crossing pair over
$(X,D)$ be a proper normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $V\subset X$ be an open subset such that
$V\subset X$ be an open subset such that ![]() $Z:=X\setminus V$ is a divisor and put
$Z:=X\setminus V$ is a divisor and put ![]() $D_V:=V\cap D$. Let
$D_V:=V\cap D$. Let ![]() $j : (V,D_V) \to (Y,E)$ be a dense open immersion where
$j : (V,D_V) \to (Y,E)$ be a dense open immersion where ![]() $(Y,E)$ is a proper normal crossing pair over
$(Y,E)$ is a proper normal crossing pair over ![]() $k$ with
$k$ with ![]() $Y\setminus E=V\setminus D_V$. Then for every effective divisor
$Y\setminus E=V\setminus D_V$. Then for every effective divisor ![]() $R$ supported on
$R$ supported on ![]() $D$, there exists an effective divisor
$D$, there exists an effective divisor ![]() $S$ supported on
$S$ supported on ![]() $E$ depending only on
$E$ depending only on ![]() $V$, on
$V$, on ![]() $j : (V,D_V) \to (Y,E)$ and linearly on
$j : (V,D_V) \to (Y,E)$ and linearly on ![]() $R$ such that for every object
$R$ such that for every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}(X,D,R)$, the connection
$\operatorname {MIC}(X,D,R)$, the connection ![]() $j_* \mathcal {M}|_V$ is an object of
$j_* \mathcal {M}|_V$ is an object of ![]() $\operatorname {MIC}(Y,E,S)$.
$\operatorname {MIC}(Y,E,S)$.
Proof. Let ![]() $p : Y'\to X$ be a resolution of
$p : Y'\to X$ be a resolution of ![]() $Z$ relative to
$Z$ relative to ![]() $D$. Put
$D$. Put ![]() $F:=(p^{-1}(Z\cup D))_{\mathrm {red}}$. In particular,
$F:=(p^{-1}(Z\cup D))_{\mathrm {red}}$. In particular, ![]() $p : Y'\to X$ induces an isomorphism
$p : Y'\to X$ induces an isomorphism ![]() $p^{-1}(V)\to V$. Furthermore,
$p^{-1}(V)\to V$. Furthermore, ![]() $Y'\setminus F=V\setminus D_V$. Hence, the normal crossing pair
$Y'\setminus F=V\setminus D_V$. Hence, the normal crossing pair ![]() $(Y',F)$ is a compactification of
$(Y',F)$ is a compactification of ![]() $V\setminus D_V$. By assumption,
$V\setminus D_V$. By assumption, ![]() $(Y,E)$ is also a compactification of
$(Y,E)$ is also a compactification of ![]() $V\setminus D_V$. Let
$V\setminus D_V$. Let ![]() $\jmath : V\setminus D_V \to V$ be the inclusion. Let
$\jmath : V\setminus D_V \to V$ be the inclusion. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D,R)$. From Lemma 3.6, the connection
$\operatorname {MIC}(X,D,R)$. From Lemma 3.6, the connection ![]() $(p^+ \mathcal {M})(\ast F)$ is an object of
$(p^+ \mathcal {M})(\ast F)$ is an object of ![]() $\operatorname {MIC}(Y',F,p^*R)$. Proposition 2.4 applied to
$\operatorname {MIC}(Y',F,p^*R)$. Proposition 2.4 applied to ![]() $V\setminus D_V$,
$V\setminus D_V$, ![]() $(Y',F)$,
$(Y',F)$, ![]() $(Y,E)$ and
$(Y,E)$ and ![]() $p^*R$ yields the existence of an effective divisor
$p^*R$ yields the existence of an effective divisor ![]() $S$ of
$S$ of ![]() $Y$ supported on
$Y$ supported on ![]() $E$ depending only on
$E$ depending only on ![]() $(Y',F)$,
$(Y',F)$, ![]() $(Y,E)$ and linearly on
$(Y,E)$ and linearly on ![]() $p^*R$ such that
$p^*R$ such that
is an object of ![]() $\operatorname {MIC}(Y,E,S)$. We thus have
$\operatorname {MIC}(Y,E,S)$. We thus have ![]() $\mathcal {N}|_V\simeq \mathcal {M}|_V$ and
$\mathcal {N}|_V\simeq \mathcal {M}|_V$ and ![]() $S$ only depends on
$S$ only depends on ![]() $V$, on
$V$, on ![]() $j : (V,D_V) \to (Y,E)$ and on
$j : (V,D_V) \to (Y,E)$ and on ![]() $R$. This concludes the proof of Proposition 3.7.
$R$. This concludes the proof of Proposition 3.7.
3.3 Resolution and multiplicity estimate
If ![]() $X$ is a smooth connected variety over
$X$ is a smooth connected variety over ![]() $k$, we recall from § 1.13 that any Cartier divisor on
$k$, we recall from § 1.13 that any Cartier divisor on ![]() $X$ can be seen as a
$X$ can be seen as a ![]() $\mathbb {Z}$-valued function on
$\mathbb {Z}$-valued function on ![]() $\operatorname {ZR}^{\operatorname {divis}}(X)$ via the injection
$\operatorname {ZR}^{\operatorname {divis}}(X)$ via the injection ![]() $\textbf {CDiv}(X)\to \textbf {Div}(X)$.
$\textbf {CDiv}(X)\to \textbf {Div}(X)$.
Lemma 3.8 Let ![]() $(X,D)$ be a normal crossing pair of dimension
$(X,D)$ be a normal crossing pair of dimension ![]() $d$ over
$d$ over ![]() $k$. Let
$k$. Let ![]() $C$ be a smooth subscheme of
$C$ be a smooth subscheme of ![]() $X$ which has simultaneously only normal crossing with
$X$ which has simultaneously only normal crossing with ![]() $D$. Let
$D$. Let ![]() $v$ be the divisorial valuation associated to the exceptional divisor of the blow-up
$v$ be the divisorial valuation associated to the exceptional divisor of the blow-up ![]() $p : Y\to X$ along
$p : Y\to X$ along ![]() $C$. Then,
$C$. Then, ![]() $D(v)\leq d$. If
$D(v)\leq d$. If ![]() $D$ is smooth, then
$D$ is smooth, then ![]() $D(v)$ is
$D(v)$ is ![]() $0$ or
$0$ or ![]() $1$.
$1$.
Proof. The question is étale local around the generic point of ![]() $C$. We can thus suppose the existence of a local system of coordinates
$C$. We can thus suppose the existence of a local system of coordinates ![]() $(x_1,\ldots, x_d)$ such that
$(x_1,\ldots, x_d)$ such that ![]() $\mathcal {I}_{D}$ is generated by
$\mathcal {I}_{D}$ is generated by ![]() $\prod _{i\in I} x_i$ where
$\prod _{i\in I} x_i$ where ![]() $I\subset \{1,\ldots, d\}$ and
$I\subset \{1,\ldots, d\}$ and ![]() $\mathcal {I}_{C}$ is generated by some
$\mathcal {I}_{C}$ is generated by some ![]() $x_j$ for
$x_j$ for ![]() $j\in J\subset \{1,\ldots, d\}$. Then
$j\in J\subset \{1,\ldots, d\}$. Then
 \[ \mathcal{I}_D=\bigg(\prod_{i\in I\cap J} x_i\prod_{i\in I\setminus I\cap J} x_i \bigg). \]
\[ \mathcal{I}_D=\bigg(\prod_{i\in I\cap J} x_i\prod_{i\in I\setminus I\cap J} x_i \bigg). \]
Since ![]() $D(v)$ is simply the multiplicity of
$D(v)$ is simply the multiplicity of ![]() $p^*D$ along the exceptional divisor, we deduce
$p^*D$ along the exceptional divisor, we deduce
If ![]() $D$ is smooth, then
$D$ is smooth, then ![]() $I\cap J$ is either empty or a singleton depending on whether
$I\cap J$ is either empty or a singleton depending on whether ![]() $D$ contains
$D$ contains ![]() $C$, and Lemma 3.8 follows.
$C$, and Lemma 3.8 follows.
The following lemma appeared as Proposition 4.3.2 in [Reference TeyssierTey16] with the tacit assumption that ![]() $D$ has simple normal crossing. If some components of
$D$ has simple normal crossing. If some components of ![]() $D$ are singular, the coefficient
$D$ are singular, the coefficient ![]() $\operatorname {fdeg} R$ is not enough and has to be replaced by
$\operatorname {fdeg} R$ is not enough and has to be replaced by ![]() $d\cdot (\operatorname {fdeg} R)$ where
$d\cdot (\operatorname {fdeg} R)$ where ![]() $d$ is the dimension of the ambient variety. We spell out the proof here for completeness.
$d$ is the dimension of the ambient variety. We spell out the proof here for completeness.
Lemma 3.9 Let ![]() $(X,D)$ be a normal crossing pair of dimension
$(X,D)$ be a normal crossing pair of dimension ![]() $d$ over
$d$ over ![]() $k$. Let
$k$. Let ![]() $R$ be an effective divisor supported on
$R$ be an effective divisor supported on ![]() $D$. Let
$D$. Let ![]() $Z$ be an effective Cartier divisor on
$Z$ be an effective Cartier divisor on ![]() $X$. Let
$X$. Let ![]() $p: Y\to X$ be a composition of blow-up which are admissible with respect to the successive transforms of
$p: Y\to X$ be a composition of blow-up which are admissible with respect to the successive transforms of ![]() $(Z,D)$. Let
$(Z,D)$. Let ![]() $v$ be a divisorial valuation centred at a component of
$v$ be a divisorial valuation centred at a component of ![]() $Z(Y)=p^*Z$. Then,
$Z(Y)=p^*Z$. Then,
where ![]() $R$ and
$R$ and ![]() $Z$ are viewed as
$Z$ are viewed as ![]() $b$-divisors via
$b$-divisors via ![]() $\textbf {CDiv}(X)\to \textbf {Div}(X)$.
$\textbf {CDiv}(X)\to \textbf {Div}(X)$.
Proof. We argue by induction on the number ![]() $n$ of admissible blow-up needed to write
$n$ of admissible blow-up needed to write ![]() $p$. If
$p$. If ![]() $n=0$, there is nothing to prove. Let us now treat the case of
$n=0$, there is nothing to prove. Let us now treat the case of ![]() $n+1$ blow-ups. Let
$n+1$ blow-ups. Let
where ![]() $r$ is a composition of
$r$ is a composition of ![]() $n$ blow-up admissible with respect to the successive transforms of
$n$ blow-up admissible with respect to the successive transforms of ![]() $(Z,D)$, and where
$(Z,D)$, and where ![]() $q$ is admissible with respect to the final transform
$q$ is admissible with respect to the final transform ![]() $(Z',D')$ of
$(Z',D')$ of ![]() $(Z,D)$ by
$(Z,D)$ by ![]() $r$. Let
$r$. Let ![]() $\mathcal {C}$ be the set of strict transforms in
$\mathcal {C}$ be the set of strict transforms in ![]() $X'$ of the exceptional divisors that appear in
$X'$ of the exceptional divisors that appear in ![]() $r$. For
$r$. For ![]() $E\in \mathcal {C}$, we let
$E\in \mathcal {C}$, we let ![]() $v_E$ be the associated divisorial valuation. In what follows, the notation
$v_E$ be the associated divisorial valuation. In what follows, the notation ![]() $'$ indicates a strict transform in
$'$ indicates a strict transform in ![]() $X'$ and
$X'$ and ![]() $''$ indicates a strict transform in
$''$ indicates a strict transform in ![]() $Y$. Write
$Y$. Write ![]() $R= \alpha _1 D_1+\cdots + \alpha _m D_m$ with
$R= \alpha _1 D_1+\cdots + \alpha _m D_m$ with ![]() $\alpha _i>0$ and
$\alpha _i>0$ and ![]() $Z= \beta _1 Z_1+\cdots +\beta _k Z_k$ with
$Z= \beta _1 Z_1+\cdots +\beta _k Z_k$ with ![]() $\beta _i>0$. We have
$\beta _i>0$. We have
with ![]() $Z(v_E)>0$ by admissibility of
$Z(v_E)>0$ by admissibility of ![]() $r$ with respect to the successive transforms of
$r$ with respect to the successive transforms of ![]() $(Z,D)$, and
$(Z,D)$, and
We have to detail the effect of ![]() $q^*$ on each component contributing to the above equalities. Let
$q^*$ on each component contributing to the above equalities. Let ![]() $C$ be the centre of
$C$ be the centre of ![]() $q$ and let
$q$ and let ![]() $P$ be its exceptional divisor with associated valuation
$P$ be its exceptional divisor with associated valuation ![]() $v_P$. Let
$v_P$. Let ![]() $E\in \mathcal {C}$. Since
$E\in \mathcal {C}$. Since ![]() $C$ and
$C$ and ![]() $E$ have simultaneously only normal crossing and since
$E$ have simultaneously only normal crossing and since ![]() $E$ is smooth, Lemma 3.8 gives
$E$ is smooth, Lemma 3.8 gives ![]() $q^{\ast } E=E''+ \epsilon _E P$ where
$q^{\ast } E=E''+ \epsilon _E P$ where ![]() $\epsilon _E\in \{0,1\}$. Since
$\epsilon _E\in \{0,1\}$. Since ![]() $C$ and
$C$ and ![]() $D'_i$ have simultaneously only normal crossing, Lemma 3.8 gives again
$D'_i$ have simultaneously only normal crossing, Lemma 3.8 gives again
Furthermore, let us write
We have
 \[ Z(Y)=\sum \beta_i Z''_{i}+\displaystyle{\sum_{E\in \mathcal{C}}} Z(v_E) E''+\bigg(\sum \beta_i \mu_i+\sum_{E\in \mathcal{C}} \epsilon_E Z(v_E) \bigg)P \]
\[ Z(Y)=\sum \beta_i Z''_{i}+\displaystyle{\sum_{E\in \mathcal{C}}} Z(v_E) E''+\bigg(\sum \beta_i \mu_i+\sum_{E\in \mathcal{C}} \epsilon_E Z(v_E) \bigg)P \]
and
 \[ R(Y)=\sum \alpha_i D''_{i}+\displaystyle{\sum_{E\in \mathcal{C}}} R(v_E) E''+\bigg(\sum \alpha_i \epsilon_i+\sum_{E\in \mathcal{C}} \epsilon_E R(v_E) \bigg)P. \]
\[ R(Y)=\sum \alpha_i D''_{i}+\displaystyle{\sum_{E\in \mathcal{C}}} R(v_E) E''+\bigg(\sum \alpha_i \epsilon_i+\sum_{E\in \mathcal{C}} \epsilon_E R(v_E) \bigg)P. \]
By recursion assumption, we have to check the inequality (3.10) for ![]() $v=v_P$. By admissibility of
$v=v_P$. By admissibility of ![]() $q$ with respect to
$q$ with respect to ![]() $(Z',D')$, the centre
$(Z',D')$, the centre ![]() $C$ lies in
$C$ lies in ![]() $Z'_{\mathrm {red}}$, that is in one of the
$Z'_{\mathrm {red}}$, that is in one of the ![]() $Z'_{i}$. Hence, one of the
$Z'_{i}$. Hence, one of the ![]() $\mu _i$ is strictly positive. Thus,
$\mu _i$ is strictly positive. Thus,
 \begin{align*} d\cdot (\operatorname{fdeg} R)\cdot Z(v_P) & =d\cdot (\operatorname{fdeg} R)\cdot \bigg(\sum \beta_i \mu_i+\sum \epsilon_E Z(v_E) \bigg) \\ &\geq d \cdot (\operatorname{fdeg} R)+\sum \epsilon_E \big(d \cdot (\operatorname{fdeg} R)\cdot Z(v_E)\big) \\ &\geq \sum \alpha_i \epsilon_i+\sum \epsilon_E R(v_E)=R(v_P) \end{align*}
\begin{align*} d\cdot (\operatorname{fdeg} R)\cdot Z(v_P) & =d\cdot (\operatorname{fdeg} R)\cdot \bigg(\sum \beta_i \mu_i+\sum \epsilon_E Z(v_E) \bigg) \\ &\geq d \cdot (\operatorname{fdeg} R)+\sum \epsilon_E \big(d \cdot (\operatorname{fdeg} R)\cdot Z(v_E)\big) \\ &\geq \sum \alpha_i \epsilon_i+\sum \epsilon_E R(v_E)=R(v_P) \end{align*}
and the proof of Lemma 3.9 is complete.
3.4 Nearby slopes for  $\mathcal {D}$-modules
$\mathcal {D}$-modules
Let ![]() $X$ be a smooth algebraic variety over
$X$ be a smooth algebraic variety over ![]() $k$. Let
$k$. Let ![]() $f$ be a non-constant function on
$f$ be a non-constant function on ![]() $X$. We denote by
$X$. We denote by ![]() $\psi _f$ the nearby cycles functor associated to
$\psi _f$ the nearby cycles functor associated to ![]() $f$. For a general reference on nearby cycles, see [Reference Maisonobe and MebkhoutMM04]. Inspired by a letter of Deligne to Malgrange [Reference DeligneDel07], the following notion of slopes was defined in [Reference TeyssierTey16].
$f$. For a general reference on nearby cycles, see [Reference Maisonobe and MebkhoutMM04]. Inspired by a letter of Deligne to Malgrange [Reference DeligneDel07], the following notion of slopes was defined in [Reference TeyssierTey16].
Definition 3.11 Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. The nearby slopes of
$\mathcal {D}_X$-module. The nearby slopes of ![]() $\mathcal {M}$ associated to
$\mathcal {M}$ associated to ![]() $f$ are the rationals
$f$ are the rationals ![]() $r\geq 0$ such that there exists a germ
$r\geq 0$ such that there exists a germ ![]() $N$ of meromorphic connection at
$N$ of meromorphic connection at ![]() $0$ in
$0$ in ![]() $\mathbb {A}^1$ with slope
$\mathbb {A}^1$ with slope ![]() $r$ verifying
$r$ verifying
We denote by ![]() $\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M})$ the set of nearby slopes of
$\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M})$ the set of nearby slopes of ![]() $\mathcal {M}$ associated to
$\mathcal {M}$ associated to ![]() $f$.
$f$.
Remark 3.13 Since ![]() $N$ is localized at
$N$ is localized at ![]() $0$, the connection
$0$, the connection ![]() $f^+N$ is localized along
$f^+N$ is localized along ![]() $\operatorname {div} f$. Hence,
$\operatorname {div} f$. Hence, ![]() $\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M})=\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M}(\ast Z))$ where
$\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M})=\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M}(\ast Z))$ where ![]() $Z$ denotes the support of
$Z$ denotes the support of ![]() $\operatorname {div} f$.
$\operatorname {div} f$.
Remark 3.14 The nearby slopes are sensitive to the non reduced structure of ![]() $\operatorname {div} f$.
$\operatorname {div} f$.
For ![]() $f$ as above, Deligne proved that the set
$f$ as above, Deligne proved that the set ![]() $\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M})$ is finite. The following theorem is the main result of [Reference TeyssierTey16].
$\operatorname {Sl}_{f}^{\operatorname {nb}}(\mathcal {M})$ is finite. The following theorem is the main result of [Reference TeyssierTey16].
Theorem 3.15 Let ![]() $X$ be a smooth algebraic variety over
$X$ be a smooth algebraic variety over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Then, there is an integer
$\mathcal {D}_X$-module. Then, there is an integer ![]() $C$ depending only on
$C$ depending only on ![]() $\mathcal {M}$ such that for every non-constant function
$\mathcal {M}$ such that for every non-constant function ![]() $f$ on
$f$ on ![]() $X$, the set
$X$, the set ![]() $\operatorname {Sl}^{\operatorname {nb}}_f(\mathcal {M})$ is bounded by
$\operatorname {Sl}^{\operatorname {nb}}_f(\mathcal {M})$ is bounded by ![]() $C$.
$C$.
In this paper, we will need a boundedness of a different kind where ![]() $f$ is fixed but where
$f$ is fixed but where ![]() $\mathcal {M}$ is allowed to vary over the objects of
$\mathcal {M}$ is allowed to vary over the objects of ![]() $\operatorname {MIC}(X,D,R)$ where
$\operatorname {MIC}(X,D,R)$ where ![]() $D$ is a normal crossing divisor and where
$D$ is a normal crossing divisor and where ![]() $R$ is an effective divisor supported on
$R$ is an effective divisor supported on ![]() $D$.
$D$.
Examples of this kind of bound were obtained in the étale setting in [Reference Hu and TeyssierHT21] and [Reference HuHu23] in a semi-stable situation where the horizontal ramification is tame. In our case, the horizontal irregularity will be allowed to be non-trivial. The price to pay for this generality will be to require that the zero locus of ![]() $f$ contains the turning locus of
$f$ contains the turning locus of ![]() $\mathcal {M}$. See Proposition 3.22 below.
$\mathcal {M}$. See Proposition 3.22 below.
Nearby slopes are compatible with proper push-forward. See [Reference TeyssierTey16, Theorem 3].
Proposition 3.16 Let ![]() $p : Y\to X$ be a proper morphism of smooth varieties over
$p : Y\to X$ be a proper morphism of smooth varieties over ![]() $k$. Let
$k$. Let ![]() $f$ be a non-constant function on
$f$ be a non-constant function on ![]() $X$ such that
$X$ such that ![]() $fp=0$ is a divisor of
$fp=0$ is a divisor of ![]() $Y$. Then, for every holonomic
$Y$. Then, for every holonomic ![]() $\mathcal {D}_Y$-module
$\mathcal {D}_Y$-module ![]() $\mathcal {M}$, we have
$\mathcal {M}$, we have
The following lemma is useful for dévissages.
Lemma 3.17 Let ![]() $p : (Y,E)\to (X,D)$ be a proper morphism of pairs over
$p : (Y,E)\to (X,D)$ be a proper morphism of pairs over ![]() $k$ such that the induced morphism
$k$ such that the induced morphism ![]() $Y\setminus E \to X \setminus D$ is an isomorphism. Let
$Y\setminus E \to X \setminus D$ is an isomorphism. Let ![]() $\mathcal {M}$ be an object in
$\mathcal {M}$ be an object in ![]() $\operatorname {MIC}(X,D)$. Then, the canonical morphism
$\operatorname {MIC}(X,D)$. Then, the canonical morphism ![]() $p_+ p^{+ }\mathcal {M} \to \mathcal {M}$ is an isomorphism.
$p_+ p^{+ }\mathcal {M} \to \mathcal {M}$ is an isomorphism.
Proof. Since ![]() $p$ is proper, [Reference MebkhoutMeb04, 3.6-4] ensures that the
$p$ is proper, [Reference MebkhoutMeb04, 3.6-4] ensures that the ![]() $\mathcal {D}_X$-module
$\mathcal {D}_X$-module ![]() $p_+ p^{+ }\mathcal {M}$ is an object of
$p_+ p^{+ }\mathcal {M}$ is an object of ![]() $\operatorname {MIC}(X,D)$. Then, Lemma 3.17 follows from Proposition 1.23 and base change for
$\operatorname {MIC}(X,D)$. Then, Lemma 3.17 follows from Proposition 1.23 and base change for ![]() $\mathcal {D}$-modules [Reference Hotta, Takeuchi and TanisakiHTT00, 1.7.3].
$\mathcal {D}$-modules [Reference Hotta, Takeuchi and TanisakiHTT00, 1.7.3].
Proposition 3.18 Let ![]() $p : (Y,E)\to (X,D)$ be a proper morphism of pairs over
$p : (Y,E)\to (X,D)$ be a proper morphism of pairs over ![]() $k$. Let
$k$. Let ![]() $f$ be a non-constant function on
$f$ be a non-constant function on ![]() $X$ such that
$X$ such that ![]() $fp=0$ is a divisor of
$fp=0$ is a divisor of ![]() $Y$. Let
$Y$. Let ![]() $Z$ be the support of
$Z$ be the support of ![]() $\operatorname {div} f$ and put
$\operatorname {div} f$ and put ![]() $T:= p^{-1}(Z)$. Assume that
$T:= p^{-1}(Z)$. Assume that ![]() $Y\setminus T \to X\setminus Z$ is an isomorphism. Let
$Y\setminus T \to X\setminus Z$ is an isomorphism. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then,
$\operatorname {MIC}(X,D)$. Then,
Proof. We have
The first equality follows from Remark 3.13. Since ![]() $Y\setminus T \to X\setminus Z$ is an isomorphism, the induced morphism
$Y\setminus T \to X\setminus Z$ is an isomorphism, the induced morphism ![]() $Y\setminus (T\cup E) \to X\setminus (Z\cup D)$ is an isomorphism with
$Y\setminus (T\cup E) \to X\setminus (Z\cup D)$ is an isomorphism with ![]() $\mathcal {M}(\ast Z)$ being an object of
$\mathcal {M}(\ast Z)$ being an object of ![]() $\operatorname {MIC}(X,Z\cup D)$. Hence, the second equality follows from Lemma 3.17. The last inclusion follows from Proposition 3.16. Proposition 3.18 is thus proved.
$\operatorname {MIC}(X,Z\cup D)$. Hence, the second equality follows from Lemma 3.17. The last inclusion follows from Proposition 3.16. Proposition 3.18 is thus proved.
Over curves, nearby slopes coincide with the traditional notion of slopes recalled in Definition 1.34. This is given by the following lemma proved in [Reference TeyssierTey16, 3.3.1].
Lemma 3.19 Let ![]() $C$ be a smooth curve over
$C$ be a smooth curve over ![]() $k$. Let
$k$. Let ![]() $0$ be a point in
$0$ be a point in ![]() $C$ and let
$C$ and let ![]() $t$ be a local uniformizer of
$t$ be a local uniformizer of ![]() $C$ at
$C$ at ![]() $0$. Let
$0$. Let ![]() $\mathcal {M}$ be an object in
$\mathcal {M}$ be an object in ![]() $\operatorname {MIC}(C,0)$. Then the nearby slopes of
$\operatorname {MIC}(C,0)$. Then the nearby slopes of ![]() $\mathcal {M}$ associated to
$\mathcal {M}$ associated to ![]() $t$ are the slopes of
$t$ are the slopes of ![]() $\mathcal {M}$ at
$\mathcal {M}$ at ![]() $0$ in the sense of Definition 1.34.
$0$ in the sense of Definition 1.34.
3.5 Boundedness of nearby slopes
In this paragraph, we will need to resolve the turning locus of a connection ![]() $\mathcal {M}$ while resolving a fixed subscheme relatively to the pole locus. Combined with Kedlaya's Theorem 1.44, this resolution gives some control on the nearby slopes of
$\mathcal {M}$ while resolving a fixed subscheme relatively to the pole locus. Combined with Kedlaya's Theorem 1.44, this resolution gives some control on the nearby slopes of ![]() $\mathcal {M}$. The existence of this resolution is achieved by the following.
$\mathcal {M}$. The existence of this resolution is achieved by the following.
Lemma 3.20 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $Z$ be a divisor of
$Z$ be a divisor of ![]() $X$ such that
$X$ such that ![]() $\operatorname {TL}(\mathcal {M})\subset Z_{\mathrm {red}}$. Then, there is a morphism of normal crossing pairs
$\operatorname {TL}(\mathcal {M})\subset Z_{\mathrm {red}}$. Then, there is a morphism of normal crossing pairs ![]() $p : (Y,E)\to (X,D)$ such that
$p : (Y,E)\to (X,D)$ such that ![]() $p:Y\to X$ is a resolution of
$p:Y\to X$ is a resolution of ![]() $Z$ relative to
$Z$ relative to ![]() $D$ and
$D$ and ![]() $p^+\mathcal {M}$ has good formal structure.
$p^+\mathcal {M}$ has good formal structure.
Proof. From the Kedlaya–Mochizuki Theorem 1.32, there exists a morphism of smooth algebraic varieties ![]() $q :Y'\to X$ obtained as a composition of blow-up above
$q :Y'\to X$ obtained as a composition of blow-up above ![]() $\operatorname {TL}(\mathcal {M})$ such that
$\operatorname {TL}(\mathcal {M})$ such that ![]() $E'=q^{-1}(D)$ is a normal crossing divisor of
$E'=q^{-1}(D)$ is a normal crossing divisor of ![]() $Y'$ and
$Y'$ and ![]() $q^+\mathcal {M}$ admits good formal structure along
$q^+\mathcal {M}$ admits good formal structure along ![]() $E'$. From [Sta-a, 080B], there is a closed subscheme
$E'$. From [Sta-a, 080B], there is a closed subscheme ![]() $T$ of
$T$ of ![]() $X$ with
$X$ with ![]() $T_{\mathrm {red}}\subset \operatorname {TL}(\mathcal {M})$ such that
$T_{\mathrm {red}}\subset \operatorname {TL}(\mathcal {M})$ such that ![]() $q:Y'\to X$ identifies with the blow-up of
$q:Y'\to X$ identifies with the blow-up of ![]() $X$ along
$X$ along ![]() $T$. By the universal property of the blow-up,
$T$. By the universal property of the blow-up, ![]() $q:Y'\to X$ is a final object in the full subcategory of schemes over
$q:Y'\to X$ is a final object in the full subcategory of schemes over ![]() $X$ consisting in morphisms
$X$ consisting in morphisms ![]() $Y''\to X$ such that the inverse image of
$Y''\to X$ such that the inverse image of ![]() $T$ is an effective Cartier divisor on
$T$ is an effective Cartier divisor on ![]() $Y''$. By assumption, we have
$Y''$. By assumption, we have ![]() $T_{\mathrm {red}}\subset \operatorname {TL}(\mathcal {M})\subset Z_{\mathrm {red}}$. Since
$T_{\mathrm {red}}\subset \operatorname {TL}(\mathcal {M})\subset Z_{\mathrm {red}}$. Since ![]() $Z$ is a divisor and since
$Z$ is a divisor and since ![]() $\operatorname {TL}(\mathcal {M})$ has pure codimension 2 in
$\operatorname {TL}(\mathcal {M})$ has pure codimension 2 in ![]() $X$ in virtue of Theorem 1.31,
$X$ in virtue of Theorem 1.31, ![]() $\operatorname {TL}(\mathcal {M})$ is nowhere dense in
$\operatorname {TL}(\mathcal {M})$ is nowhere dense in ![]() $Z_{\mathrm {red}}$. Hence,
$Z_{\mathrm {red}}$. Hence, ![]() $T_{\mathrm {red}}$ is nowhere dense in
$T_{\mathrm {red}}$ is nowhere dense in ![]() $Z_{\mathrm {red}}$. Thus, Lemma 3.5 applies. That is, there exists a resolution
$Z_{\mathrm {red}}$. Thus, Lemma 3.5 applies. That is, there exists a resolution ![]() $p : Y\to X$ of
$p : Y\to X$ of ![]() $Z$ relative to
$Z$ relative to ![]() $D$ such that the pull-back scheme
$D$ such that the pull-back scheme ![]() $p^{-1}(T)$ is an effective Cartier divisor on
$p^{-1}(T)$ is an effective Cartier divisor on ![]() $Y$. Put
$Y$. Put ![]() $E=p^{-1}(D)$. Then, there is the following canonical commutative diagram of normal crossing pairs.
$E=p^{-1}(D)$. Then, there is the following canonical commutative diagram of normal crossing pairs.

From Proposition 1.30, the connection ![]() $h^+(q^+\mathcal {M})\simeq p^+\mathcal {M}$ has good formal structure and the proof of Lemma 3.20 is complete.
$h^+(q^+\mathcal {M})\simeq p^+\mathcal {M}$ has good formal structure and the proof of Lemma 3.20 is complete.
We recall the following boundedness result for nearby slopes, formulated in terms of the highest slope ![]() $b$-divisor from Remark 1.42. See [Reference TeyssierTey16, 3.4.1] for a proof.
$b$-divisor from Remark 1.42. See [Reference TeyssierTey16, 3.4.1] for a proof.
Lemma 3.21 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$ with good formal structure. Let
$\operatorname {MIC}(X,D)$ with good formal structure. Let ![]() $f$ be a non-constant function on
$f$ be a non-constant function on ![]() $X$ such that
$X$ such that ![]() $\operatorname {div} f$ is supported on
$\operatorname {div} f$ is supported on ![]() $D$. Let
$D$. Let ![]() $r\in \mathbb {Q}_{\geq 0}$ such that for every divisorial valuation
$r\in \mathbb {Q}_{\geq 0}$ such that for every divisorial valuation ![]() $v$ centred at an irreducible component of
$v$ centred at an irreducible component of ![]() $\operatorname {div} f$, we have
$\operatorname {div} f$, we have
where ![]() $R(\mathcal {M})$ is the highest slope
$R(\mathcal {M})$ is the highest slope ![]() $b$-divisor from Remark 1.42. Then the nearby slopes of
$b$-divisor from Remark 1.42. Then the nearby slopes of ![]() $\mathcal {M}$ associated to
$\mathcal {M}$ associated to ![]() $f$ are smaller than
$f$ are smaller than ![]() $r$.
$r$.
Proposition 3.22 Let ![]() $(X,D)$ be a normal crossing pair of dimension
$(X,D)$ be a normal crossing pair of dimension ![]() $d$ over
$d$ over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $f$ be a non-constant function on
$f$ be a non-constant function on ![]() $X$. Suppose that the turning locus of
$X$. Suppose that the turning locus of ![]() $\mathcal {M}$ lies in the support of
$\mathcal {M}$ lies in the support of ![]() $\operatorname {div} f$. Then, the nearby slopes of
$\operatorname {div} f$. Then, the nearby slopes of ![]() $\mathcal {M}$ associated to
$\mathcal {M}$ associated to ![]() $f$ are bounded by
$f$ are bounded by ![]() $d\cdot \operatorname {fdeg} \operatorname {Irr}(X,\mathcal {M})$.
$d\cdot \operatorname {fdeg} \operatorname {Irr}(X,\mathcal {M})$.
Proof. Put ![]() $Z:=\operatorname {div} f$. Since
$Z:=\operatorname {div} f$. Since ![]() $\operatorname {TL}(\mathcal {M})\subset Z_{\mathrm {red}}$, Lemma 3.20 ensures the existence of a morphism of normal crossing pairs
$\operatorname {TL}(\mathcal {M})\subset Z_{\mathrm {red}}$, Lemma 3.20 ensures the existence of a morphism of normal crossing pairs ![]() $p : (Y,E)\to (X,D)$ such that
$p : (Y,E)\to (X,D)$ such that ![]() $p:Y\to X$ is a resolution of
$p:Y\to X$ is a resolution of ![]() $Z$ relative to
$Z$ relative to ![]() $D$ and
$D$ and ![]() $p^+\mathcal {M}$ has good formal structure. Let
$p^+\mathcal {M}$ has good formal structure. Let ![]() $T:= p^{-1}(Z)=p^*\operatorname {div} f=\operatorname {div} fp$ be the pull-back scheme. Let
$T:= p^{-1}(Z)=p^*\operatorname {div} f=\operatorname {div} fp$ be the pull-back scheme. Let ![]() $(Z',D')$ be the transform of
$(Z',D')$ be the transform of ![]() $(Z,D)$ by
$(Z,D)$ by ![]() $p$. Since
$p$. Since ![]() $Z$ is a divisor, so is
$Z$ is a divisor, so is ![]() $Z'$. By assumption,
$Z'$. By assumption, ![]() $Z'$ and
$Z'$ and ![]() $D'$ have only simultaneously normal crossing. Thus,
$D'$ have only simultaneously normal crossing. Thus, ![]() $Z'\cup D'$ is a normal crossing divisor of
$Z'\cup D'$ is a normal crossing divisor of ![]() $Y$. Since
$Y$. Since ![]() $Z'\cup D'$ and
$Z'\cup D'$ and ![]() $T\cup E$ have the same support, we deduce that
$T\cup E$ have the same support, we deduce that ![]() $T\cup E$ is a normal crossing divisor of
$T\cup E$ is a normal crossing divisor of ![]() $Y$. We are going to apply Lemma 3.21 on
$Y$. We are going to apply Lemma 3.21 on ![]() $(Y,T\cup E)$ to
$(Y,T\cup E)$ to ![]() $(p^+\mathcal {M})(\ast T)$ and
$(p^+\mathcal {M})(\ast T)$ and ![]() $fp$. Since
$fp$. Since ![]() $p^+\mathcal {M} \in \operatorname {MIC}(Y,E)$ has good formal structure, so does
$p^+\mathcal {M} \in \operatorname {MIC}(Y,E)$ has good formal structure, so does ![]() $(p^+\mathcal {M})(\ast T) \in \operatorname {MIC}(Y,T\cup E)$. By assumption,
$(p^+\mathcal {M})(\ast T) \in \operatorname {MIC}(Y,T\cup E)$. By assumption, ![]() $\operatorname {div} fp$ is supported on
$\operatorname {div} fp$ is supported on ![]() $T\cup E$. Let
$T\cup E$. Let ![]() $v$ be a divisorial valuation centred at an irreducible component of
$v$ be a divisorial valuation centred at an irreducible component of ![]() $T=\operatorname {div} fp$. If the centre of
$T=\operatorname {div} fp$. If the centre of ![]() $v$ is not a component of
$v$ is not a component of ![]() $E$, we have
$E$, we have
Otherwise, ![]() $R((p^+\mathcal {M})(\ast T))(v)=R(\mathcal {M})(v)$. On the other hand, we have
$R((p^+\mathcal {M})(\ast T))(v)=R(\mathcal {M})(v)$. On the other hand, we have
 \begin{align*} R(\mathcal{M})(v)& \leq (\operatorname{Irr} \mathcal{M})(v)\\ & \leq (\operatorname{Irr}(X,\mathcal{M}))(v)\\ & \leq d \cdot (\operatorname{fdeg} \operatorname{Irr}(X,\mathcal{M})) \cdot (\operatorname{div} f)(v), \end{align*}
\begin{align*} R(\mathcal{M})(v)& \leq (\operatorname{Irr} \mathcal{M})(v)\\ & \leq (\operatorname{Irr}(X,\mathcal{M}))(v)\\ & \leq d \cdot (\operatorname{fdeg} \operatorname{Irr}(X,\mathcal{M})) \cdot (\operatorname{div} f)(v), \end{align*}
where the first inequality is trivial, the second follows from Kedlaya's Theorem 1.44 and where the last inequality comes from Lemma 3.9. From Lemma 3.21, we deduce that the nearby slopes of ![]() $(p^+\mathcal {M})(\ast T)$ associated to
$(p^+\mathcal {M})(\ast T)$ associated to ![]() $fp$ are bounded by
$fp$ are bounded by ![]() $d \cdot (\operatorname {fdeg} \operatorname {Irr}(X,\mathcal {M}))$. Finally, Proposition 3.18 applied to the proper morphism of pairs
$d \cdot (\operatorname {fdeg} \operatorname {Irr}(X,\mathcal {M}))$. Finally, Proposition 3.18 applied to the proper morphism of pairs ![]() $p : (Y,E)\to (X,D)$ yields
$p : (Y,E)\to (X,D)$ yields
which concludes the proof of Proposition 3.22.
Proposition 3.23 Let ![]() $(X,D)$ be a normal crossing pair of dimension
$(X,D)$ be a normal crossing pair of dimension ![]() $d$ over
$d$ over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $C$ be a smooth connected curve over
$C$ be a smooth connected curve over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $f : X\to C$ be a dominant proper morphism. Let
$f : X\to C$ be a dominant proper morphism. Let ![]() $0$ be a closed point in
$0$ be a closed point in ![]() $C$. Suppose that the reduced fibre
$C$. Suppose that the reduced fibre ![]() $Z$ of
$Z$ of ![]() $f$ over
$f$ over ![]() $0$ is not empty and is contained in
$0$ is not empty and is contained in ![]() $D$. Suppose that cohomological boundedness holds with bound
$D$. Suppose that cohomological boundedness holds with bound ![]() $K$ for the generic fibre of
$K$ for the generic fibre of ![]() $f : X\to C$. Then for every effective divisor
$f : X\to C$. Then for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$ with
$\operatorname {MIC}_r(X,D,R)$ with ![]() $\operatorname {TL}(\mathcal {M})\subset Z$, we have
$\operatorname {TL}(\mathcal {M})\subset Z$, we have
where ![]() $R_{\eta }$ is the pull-back of
$R_{\eta }$ is the pull-back of ![]() $R$ to the generic fibre of
$R$ to the generic fibre of ![]() $f : X\to C$.
$f : X\to C$.
Proof. By the generic smoothness theorem, the generic fibre of ![]() $X$ over
$X$ over ![]() $C$ is smooth and the generic fibre of
$C$ is smooth and the generic fibre of ![]() $(X,D)$ over
$(X,D)$ over ![]() $C$ is again a normal crossing pair. Hence, the statement of cohomological boundedness makes sense over the generic fibre of
$C$ is again a normal crossing pair. Hence, the statement of cohomological boundedness makes sense over the generic fibre of ![]() $(X,D)$ over
$(X,D)$ over ![]() $C$. We reproduce here a reasoning carried out in [Reference TeyssierTey23, Theorem 2] in a particular case. Let
$C$. We reproduce here a reasoning carried out in [Reference TeyssierTey23, Theorem 2] in a particular case. Let ![]() $t$ be a local uniformizer of
$t$ be a local uniformizer of ![]() $C$ around
$C$ around ![]() $0$. Since
$0$. Since ![]() $Z\subset D$, we have
$Z\subset D$, we have
Since the irregularity complex commutes with proper push-forward [Reference MebkhoutMeb90], we deduce
From Theorem 1.13, the irregularity complex of a holonomic ![]() $\mathcal {D}_C$-module is a skyscraper sheaf concentrated in degree
$\mathcal {D}_C$-module is a skyscraper sheaf concentrated in degree ![]() $1$. Hence, Lemma 1.36 gives
$1$. Hence, Lemma 1.36 gives
 \begin{align*} \chi(0, \operatorname{Irr}_0^* f_+^{\operatorname{an}} \mathcal{M}^{\operatorname{an}})&= \sum (-1)^i \dim \mathcal{H}^1 \operatorname{Irr}_0^* \mathcal{H}^{i-1}f_+^{\operatorname{an}} \mathcal{M}^{\operatorname{an}} \\ & =\sum (-1)^i \operatorname{irr}(0,\mathcal{H}^{i-1} f_+^{\operatorname{an}} \mathcal{M}^{\operatorname{an}}). \end{align*}
\begin{align*} \chi(0, \operatorname{Irr}_0^* f_+^{\operatorname{an}} \mathcal{M}^{\operatorname{an}})&= \sum (-1)^i \dim \mathcal{H}^1 \operatorname{Irr}_0^* \mathcal{H}^{i-1}f_+^{\operatorname{an}} \mathcal{M}^{\operatorname{an}} \\ & =\sum (-1)^i \operatorname{irr}(0,\mathcal{H}^{i-1} f_+^{\operatorname{an}} \mathcal{M}^{\operatorname{an}}). \end{align*}
On the other hand, the properness of ![]() $f$ yields from [Reference Hotta, Takeuchi and TanisakiHTT00, 4.7.2] a canonical identification
$f$ yields from [Reference Hotta, Takeuchi and TanisakiHTT00, 4.7.2] a canonical identification ![]() $f_+^{\operatorname {an}} \mathcal {M}^{\operatorname {an}} \simeq (f_+ \mathcal {M})^{\operatorname {an}}$. Since the irregularity number at
$f_+^{\operatorname {an}} \mathcal {M}^{\operatorname {an}} \simeq (f_+ \mathcal {M})^{\operatorname {an}}$. Since the irregularity number at ![]() $0$ is a formal invariant, we deduce
$0$ is a formal invariant, we deduce
For every integer ![]() $i$, Lemma 3.19 gives
$i$, Lemma 3.19 gives
From Proposition 3.16 and the exactness of nearby cycles, we have for every ![]() $i$
$i$
We deduce
Since ![]() $Z$ contains the turning locus of
$Z$ contains the turning locus of ![]() $\mathcal {M}$, Proposition 3.22 implies that the nearby slopes of
$\mathcal {M}$, Proposition 3.22 implies that the nearby slopes of ![]() $\mathcal {M}$ associated to
$\mathcal {M}$ associated to ![]() $f$ are bounded by
$f$ are bounded by ![]() $d\cdot \operatorname {fdeg} R$. Since cohomological boundedness holds with bound
$d\cdot \operatorname {fdeg} R$. Since cohomological boundedness holds with bound ![]() $K$ for the generic fibre of
$K$ for the generic fibre of ![]() $f : X\to C$, Proposition 3.23 follows.
$f : X\to C$, Proposition 3.23 follows.
4. Partial discrepancy  $b$-divisors
$b$-divisors
Before proving cohomological boundedness for surfaces, we make a détour through the theory of ![]() $b$-divisor to introduce the partial discrepancy of a
$b$-divisor to introduce the partial discrepancy of a ![]() $b$-divisor. As usual,
$b$-divisor. As usual, ![]() $k$ denotes a field of characteristic
$k$ denotes a field of characteristic ![]() $0$.
$0$.
4.1 Chain of blow-up
Let ![]() $X$ be a smooth surface over
$X$ be a smooth surface over ![]() $k$. Let
$k$. Let ![]() $n\geq 0$. Borrowing the terminology of [Reference Cossart, Piltant and Reguera-LopezCPR02], a chain of blow-up of
$n\geq 0$. Borrowing the terminology of [Reference Cossart, Piltant and Reguera-LopezCPR02], a chain of blow-up of ![]() $X$ of length
$X$ of length ![]() $n$ is a sequence
$n$ is a sequence ![]() $\mathbf {p}$ of maps
$\mathbf {p}$ of maps
where ![]() $p_i$ is a blow-up at a single closed point
$p_i$ is a blow-up at a single closed point ![]() $P_i$ of
$P_i$ of ![]() $X_i$ with
$X_i$ with ![]() $p_i(P_{i+1})=P_i$. We let
$p_i(P_{i+1})=P_i$. We let ![]() $E_\mathbf {p}$ be the exceptional divisor of
$E_\mathbf {p}$ be the exceptional divisor of ![]() $p_{n-1}$. We denote by
$p_{n-1}$. We denote by ![]() $p : X'\to X$ the composition of the
$p : X'\to X$ the composition of the ![]() $p_i$,
$p_i$, ![]() $0\leq i\leq n-1$ and by
$0\leq i\leq n-1$ and by ![]() $\pi : X_{n-1}\to X$ the composition of the
$\pi : X_{n-1}\to X$ the composition of the ![]() $p_i$,
$p_i$, ![]() $0\leq i\leq n-2$.
$0\leq i\leq n-2$.
The following theorem was proven by Zariski [Reference ZariskiZar39] when ![]() $k$ is algebraically closed. See [Reference CossartCos97] for arbitrary
$k$ is algebraically closed. See [Reference CossartCos97] for arbitrary ![]() $k$ of characteristic
$k$ of characteristic ![]() $0$.
$0$.
Theorem 4.2 Let ![]() $X$ be a smooth connected surface over
$X$ be a smooth connected surface over ![]() $k$. Let
$k$. Let ![]() $k(X)$ be the function field of
$k(X)$ be the function field of ![]() $X$. The map associating to any chain of blow-up
$X$. The map associating to any chain of blow-up ![]() $\mathbf {p}$ of
$\mathbf {p}$ of ![]() $X$ the valuation on
$X$ the valuation on ![]() $k(X)$ induced by
$k(X)$ induced by ![]() $E_\mathbf {p}$ is a bijection between the set of chains of blow-up of
$E_\mathbf {p}$ is a bijection between the set of chains of blow-up of ![]() $X$ and
$X$ and ![]() $\operatorname {ZR}^{\operatorname {divis}}(X)$.
$\operatorname {ZR}^{\operatorname {divis}}(X)$.
The map ![]() $p : X'\to X$ corresponding to a divisorial valuation
$p : X'\to X$ corresponding to a divisorial valuation ![]() $v$ via Theorem 4.2 is the smallest modification of
$v$ via Theorem 4.2 is the smallest modification of ![]() $X$ on which the centre of
$X$ on which the centre of ![]() $v$ is a divisor. This is the following Proposition 4.4. To prove it, we need the following.
$v$ is a divisor. This is the following Proposition 4.4. To prove it, we need the following.
Lemma 4.3 Let ![]() $f : Y\to X$ be a modification between smooth connected surfaces over
$f : Y\to X$ be a modification between smooth connected surfaces over ![]() $k$. Let
$k$. Let ![]() $P$ be a closed point of
$P$ be a closed point of ![]() $X$. Then either the scheme
$X$. Then either the scheme ![]() $f^{-1}(P)$ has pure dimension
$f^{-1}(P)$ has pure dimension ![]() $1$ or
$1$ or ![]() $f^{-1}(P)$ is a single point
$f^{-1}(P)$ is a single point ![]() $Q$. In the latter case, there is a neighbourhood
$Q$. In the latter case, there is a neighbourhood ![]() $U$ of
$U$ of ![]() $P$ in
$P$ in ![]() $X$ such that the induced morphism
$X$ such that the induced morphism ![]() $f|_U: f^{-1}(U)\to U$ is an isomorphism.
$f|_U: f^{-1}(U)\to U$ is an isomorphism.
Proof. This follows from the fact [Sta-b, 0C5R] that a proper birational morphism between smooth connected surfaces is a sequence of blow-up in closed points.
Proposition 4.4 Let ![]() $X$ be a smooth connected surface over
$X$ be a smooth connected surface over ![]() $k$. Let
$k$. Let ![]() $v$ be a divisorial valuation of
$v$ be a divisorial valuation of ![]() $X$ and let
$X$ and let ![]() $f : Y\to X$ be a modification such that the centre of
$f : Y\to X$ be a modification such that the centre of ![]() $v$ on
$v$ on ![]() $Y$ is a divisor. Let
$Y$ is a divisor. Let ![]() $\mathbf {p}$ be the chain of blow-up (4.1) corresponding to
$\mathbf {p}$ be the chain of blow-up (4.1) corresponding to ![]() $v$ via Theorem 4.2. Then,
$v$ via Theorem 4.2. Then, ![]() $f$ admits a unique factorization through
$f$ admits a unique factorization through ![]() $p : X'\to X$.
$p : X'\to X$.
Proof. We argue by induction on the length ![]() $n\geq 0$ of
$n\geq 0$ of ![]() $\mathbf {p}$. If
$\mathbf {p}$. If ![]() $n=0$, there is nothing to do. Assume that
$n=0$, there is nothing to do. Assume that ![]() $n>0$ and that
$n>0$ and that ![]() $\mathbf {p}$ has length
$\mathbf {p}$ has length ![]() $n$ as in (4.1). Let
$n$ as in (4.1). Let ![]() $E$ be the centre of
$E$ be the centre of ![]() $v$ on
$v$ on ![]() $Y$. Since the centre of
$Y$. Since the centre of ![]() $v$ on
$v$ on ![]() $X$ is the point
$X$ is the point ![]() $P_0$, the map
$P_0$, the map ![]() $f$ sends
$f$ sends ![]() $E$ on
$E$ on ![]() $P_0$. In particular, the scheme
$P_0$. In particular, the scheme ![]() $f^{-1}(P_0)$ contains
$f^{-1}(P_0)$ contains ![]() $E$. From Lemma 4.3, the scheme
$E$. From Lemma 4.3, the scheme ![]() $f^{-1}(P_0)$ has pure dimension one. It is thus an effective Cartier divisor on
$f^{-1}(P_0)$ has pure dimension one. It is thus an effective Cartier divisor on ![]() $Y$. From the universal property of the blow-up, we deduce that
$Y$. From the universal property of the blow-up, we deduce that ![]() $f$ factors uniquely through
$f$ factors uniquely through ![]() $p_0 : X_1\to X$ via a modification
$p_0 : X_1\to X$ via a modification ![]() $g : Y\to X_1$. Observe that the chain
$g : Y\to X_1$. Observe that the chain
is the chain corresponding to ![]() $v$ via Theorem 4.2 applied to the smooth connected surface
$v$ via Theorem 4.2 applied to the smooth connected surface ![]() $X_1$. Since
$X_1$. Since ![]() $\mathbf {q}$ has length
$\mathbf {q}$ has length ![]() $n-1$, the recursion assumption applies to
$n-1$, the recursion assumption applies to ![]() $g : Y\to X_1$ and
$g : Y\to X_1$ and ![]() $v$ and provides a unique factorization of
$v$ and provides a unique factorization of ![]() $g$ through
$g$ through ![]() $q: X'\to X_1$. We thus get the desired factorization of
$q: X'\to X_1$. We thus get the desired factorization of ![]() $f$ through
$f$ through ![]() $p$.
$p$.
4.2 Partial discrepancy divisor
Armed with Zariski's Theorem 4.2, we are now in a position to define the partial discrepancy of a ![]() $b$-divisor on a smooth connected surface endowed with a reduced divisor. Although defined for every
$b$-divisor on a smooth connected surface endowed with a reduced divisor. Although defined for every ![]() $\mathbb {Z}$-valued function on the set of divisorial valuations, the partial discrepancy is better behaved on a subgroup of the group of
$\mathbb {Z}$-valued function on the set of divisorial valuations, the partial discrepancy is better behaved on a subgroup of the group of ![]() $b$-divisors that we now introduce.
$b$-divisors that we now introduce.
Lemma 4.5 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $Z$ be a
$Z$ be a ![]() $b$-divisor on
$b$-divisor on ![]() $X$ and let us view
$X$ and let us view ![]() $D$ as a
$D$ as a ![]() $b$-divisor via
$b$-divisor via ![]() $\operatorname {Cart}(X)\to \textbf {Div}(X)$. The following conditions are equivalent.
$\operatorname {Cart}(X)\to \textbf {Div}(X)$. The following conditions are equivalent.
(i) The support of
 $Z : \operatorname {ZR}^{\operatorname {divis}}(X)\to \mathbb {Z}$ lies in the support of
$Z : \operatorname {ZR}^{\operatorname {divis}}(X)\to \mathbb {Z}$ lies in the support of  $D : \operatorname {ZR}^{\operatorname {divis}}(X)\to \mathbb {Z}$.
$D : \operatorname {ZR}^{\operatorname {divis}}(X)\to \mathbb {Z}$.(ii) For every modification
 $f : Y\to X$, the support of
$f : Y\to X$, the support of  $Z(Y)$ is contained in the support of
$Z(Y)$ is contained in the support of  $f^*D$.
$f^*D$.
Proof. We assume that condition (i) holds. Let ![]() $f : Y\to X$ be a modification and let
$f : Y\to X$ be a modification and let ![]() $v$ be a divisorial valuation centred at a divisor in the support of
$v$ be a divisorial valuation centred at a divisor in the support of ![]() $Z(Y)$. Then
$Z(Y)$. Then ![]() $Z(v)=(Z(Y))(v)\neq 0$. Hence,
$Z(v)=(Z(Y))(v)\neq 0$. Hence, ![]() $D(v)=(f^*D)(v)\neq 0$ and condition (ii) holds. On the other hand, assume that condition (ii) holds. Let
$D(v)=(f^*D)(v)\neq 0$ and condition (ii) holds. On the other hand, assume that condition (ii) holds. Let ![]() $v$ be a divisorial valuation on
$v$ be a divisorial valuation on ![]() $X$ such that
$X$ such that ![]() $Z(v)\neq 0$. Then, there exists a modification
$Z(v)\neq 0$. Then, there exists a modification ![]() $f : Y\to X$ such that the centre
$f : Y\to X$ such that the centre ![]() $E$ of
$E$ of ![]() $v$ on
$v$ on ![]() $Y$ is a divisor. Since
$Y$ is a divisor. Since ![]() $Z(v)= m(E,Z(Y))\neq 0$, the divisor
$Z(v)= m(E,Z(Y))\neq 0$, the divisor ![]() $E$ is a component of
$E$ is a component of ![]() $Z(Y)$. By assumption, we deduce that
$Z(Y)$. By assumption, we deduce that ![]() $E$ is a component of
$E$ is a component of ![]() $f^*D$. Thus,
$f^*D$. Thus, ![]() $D(v)= m(E,f^*D)\neq 0$.
$D(v)= m(E,f^*D)\neq 0$.
Definition 4.6 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $Z$ be a
$Z$ be a ![]() $b$-divisor on
$b$-divisor on ![]() $X$. If the equivalent conditions of Lemma 4.5 are satisfied, we say that
$X$. If the equivalent conditions of Lemma 4.5 are satisfied, we say that ![]() $Z$ is a
$Z$ is a ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$. We denote by
$(X,D)$. We denote by ![]() $\textbf {Div}(X,D)$ the subgroup of
$\textbf {Div}(X,D)$ the subgroup of ![]() $\textbf {Div}(X)$ formed by
$\textbf {Div}(X)$ formed by ![]() $b$-divisors of
$b$-divisors of ![]() $(X,D)$.
$(X,D)$.
Let ![]() $Z$ be a
$Z$ be a ![]() $b$-divisor on
$b$-divisor on ![]() $(X,D)$ as in Definition 4.6. We define a new function
$(X,D)$ as in Definition 4.6. We define a new function
as follows. Let ![]() $v\in \operatorname {ZR}^{\operatorname {divis}}(X)$. Let
$v\in \operatorname {ZR}^{\operatorname {divis}}(X)$. Let ![]() $\mathbf {p}$ be the chain of blow-up of
$\mathbf {p}$ be the chain of blow-up of ![]() $X$ as in (4.1) corresponding to
$X$ as in (4.1) corresponding to ![]() $v$ via Theorem 4.2. If
$v$ via Theorem 4.2. If ![]() $n=0$ or if
$n=0$ or if ![]() $n\geq 1$ and
$n\geq 1$ and ![]() $P_{n-1}$ is a singular point of the support of
$P_{n-1}$ is a singular point of the support of ![]() $\pi ^*D$, we put
$\pi ^*D$, we put ![]() $(\delta Z)(v)=0$. Otherwise, we put
$(\delta Z)(v)=0$. Otherwise, we put
where ![]() $Z(X_{n-1})$ is viewed as a
$Z(X_{n-1})$ is viewed as a ![]() $b$-divisor via
$b$-divisor via ![]() $\operatorname {Cart}(X_{n-1})\to \textbf {Div}(X)$.
$\operatorname {Cart}(X_{n-1})\to \textbf {Div}(X)$.
Remark 4.7 Assume that ![]() $n\geq 1$ and that
$n\geq 1$ and that ![]() $P_{n-1}$ is not a singular point of the support of
$P_{n-1}$ is not a singular point of the support of ![]() $\pi ^*D$. Then, if
$\pi ^*D$. Then, if ![]() $P_{n-1}$ does not lie in the support of
$P_{n-1}$ does not lie in the support of ![]() $Z(X_{n-1})$, we have
$Z(X_{n-1})$, we have ![]() $(Z(X_{n-1}))(v)=0$. Otherwise,
$(Z(X_{n-1}))(v)=0$. Otherwise, ![]() $P_{n-1}$ lies in the support of
$P_{n-1}$ lies in the support of ![]() $Z(X_{n-1})$. Since the support of
$Z(X_{n-1})$. Since the support of ![]() $\pi ^*D$ contains that of
$\pi ^*D$ contains that of ![]() $Z(X_{n-1})$,
$Z(X_{n-1})$, ![]() $P_{n-1}$ is not a singular point of the support of
$P_{n-1}$ is not a singular point of the support of ![]() $Z(X_{n-1})$. Thus,
$Z(X_{n-1})$. Thus, ![]() $(Z(X_{n-1}))(v)$ is simply the multiplicity of the unique irreducible component of
$(Z(X_{n-1}))(v)$ is simply the multiplicity of the unique irreducible component of ![]() $Z(X_{n-1})$ passing through
$Z(X_{n-1})$ passing through ![]() $P_{n-1}$.
$P_{n-1}$.
Example 4.8 If ![]() $Z$ lies in the image of
$Z$ lies in the image of ![]() $\operatorname {Cart}(X)\to \textbf {Div}(X)$, then
$\operatorname {Cart}(X)\to \textbf {Div}(X)$, then ![]() $\delta Z=0$.
$\delta Z=0$.
Proposition 4.9 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $Z$ be a
$Z$ be a ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$. Then
$(X,D)$. Then ![]() $\delta Z$ is a
$\delta Z$ is a ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$.
$(X,D)$.
Proof. Let ![]() $f : Y\to X$ be a modification of
$f : Y\to X$ be a modification of ![]() $X$. Let
$X$. Let ![]() $v$ be a divisorial valuation centred at a divisor of
$v$ be a divisorial valuation centred at a divisor of ![]() $Y$. Let
$Y$. Let ![]() $\mathbf {p}$ be the chain of blow-up (4.1) corresponding to
$\mathbf {p}$ be the chain of blow-up (4.1) corresponding to ![]() $v$ via Theorem 4.2. Assume that
$v$ via Theorem 4.2. Assume that ![]() $n\geq 1$ and that
$n\geq 1$ and that ![]() $P_{n-1}$ is not a singular point of the support of
$P_{n-1}$ is not a singular point of the support of ![]() $\pi ^*D$. From Remark 4.7, there are two cases. If
$\pi ^*D$. From Remark 4.7, there are two cases. If ![]() $P_{n-1}$ does not lie in support of
$P_{n-1}$ does not lie in support of ![]() $Z(X_{n-1})$, then
$Z(X_{n-1})$, then
and since ![]() $Z$ is a
$Z$ is a ![]() $b$-divisor, there is only a finite number of
$b$-divisor, there is only a finite number of ![]() $v$ as above for which
$v$ as above for which ![]() $(\delta Z)(v)\neq 0$. Otherwise
$(\delta Z)(v)\neq 0$. Otherwise ![]() $P_{n-1}$ is a smooth point of the support of
$P_{n-1}$ is a smooth point of the support of ![]() $Z(X_{n-1})$. If
$Z(X_{n-1})$. If ![]() $w$ is the divisorial valuation corresponding to the unique irreducible component of
$w$ is the divisorial valuation corresponding to the unique irreducible component of ![]() $Z(X_{n-1})$ passing through
$Z(X_{n-1})$ passing through ![]() $P_{n-1}$, we thus have
$P_{n-1}$, we thus have ![]() $(Z(X_{n-1}))(v)=Z(w)$, so that
$(Z(X_{n-1}))(v)=Z(w)$, so that
On the other hand, Proposition 4.4 implies the existence of the following commutative triangle.

Since the centre of ![]() $w$ on
$w$ on ![]() $X'$ is a divisor, so is its centre on
$X'$ is a divisor, so is its centre on ![]() $Y$. Since
$Y$. Since ![]() $Z$ is a
$Z$ is a ![]() $b$-divisor, we again conclude that there is only a finite number of
$b$-divisor, we again conclude that there is only a finite number of ![]() $v$ as above for which
$v$ as above for which ![]() $(\delta Z)(v)\neq 0$. This proves that
$(\delta Z)(v)\neq 0$. This proves that ![]() $\delta Z$ is a
$\delta Z$ is a ![]() $b$-divisor of
$b$-divisor of ![]() $X$. We are left to prove that
$X$. We are left to prove that ![]() $\delta Z$ is a
$\delta Z$ is a ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$. Let
$(X,D)$. Let ![]() $v$ be a divisorial valuation with
$v$ be a divisorial valuation with ![]() $D(v)=0$. Since
$D(v)=0$. Since ![]() $Z$ is a
$Z$ is a ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$, we have
$(X,D)$, we have ![]() $Z(v)=0$ and
$Z(v)=0$ and ![]() $(Z(X_{n-1}))(v)=0$. This concludes the proof of Proposition 4.9.
$(Z(X_{n-1}))(v)=0$. This concludes the proof of Proposition 4.9.
Definition 4.10 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $Z$ be a
$Z$ be a ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$. Then
$(X,D)$. Then ![]() $\delta Z$ is called the partial discrepancy of
$\delta Z$ is called the partial discrepancy of ![]() $Z$.
$Z$.
The following proposition expresses the partial discrepancy without any reference to the chains of blow-up provided by Zariski's Theorem 4.2.
Proposition 4.11 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $Z$ be a
$Z$ be a ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$. Let
$(X,D)$. Let ![]() $f: Y\to X$ be a modification of
$f: Y\to X$ be a modification of ![]() $X$. Let
$X$. Let ![]() $Y'\to Y$ be the blow-up of
$Y'\to Y$ be the blow-up of ![]() $Y$ at a closed point
$Y$ at a closed point ![]() $P$ and let
$P$ and let ![]() $E$ be its exceptional divisor. Let
$E$ be its exceptional divisor. Let ![]() $v$ be a divisorial valuation on
$v$ be a divisorial valuation on ![]() $X$ such that the centre of
$X$ such that the centre of ![]() $v$ on
$v$ on ![]() $Y$ is
$Y$ is ![]() $P$ and the centre of
$P$ and the centre of ![]() $v$ on
$v$ on ![]() $Y'$ is
$Y'$ is ![]() $E$. If
$E$. If ![]() $P$ is a singular point of the support of
$P$ is a singular point of the support of ![]() $f^*D$, then
$f^*D$, then ![]() $(\delta Z)(v)=0$. Otherwise, we have
$(\delta Z)(v)=0$. Otherwise, we have ![]() $(\delta Z)(v)=(Z(Y))(v)-Z(v)$ where
$(\delta Z)(v)=(Z(Y))(v)-Z(v)$ where ![]() $Z(Y)$ is viewed as a
$Z(Y)$ is viewed as a ![]() $b$-divisor via
$b$-divisor via ![]() $\operatorname {Cart}(Y)\to \textbf {Div}(X)$.
$\operatorname {Cart}(Y)\to \textbf {Div}(X)$.
Proof. Let ![]() $\mathbf {p}$ be the chain of blow-up (4.1) corresponding to
$\mathbf {p}$ be the chain of blow-up (4.1) corresponding to ![]() $v$ via Theorem 4.2. We use the notation from § 4.1. Since the centre of
$v$ via Theorem 4.2. We use the notation from § 4.1. Since the centre of ![]() $v$ on
$v$ on ![]() $Y$ is a point, so is the centre of
$Y$ is a point, so is the centre of ![]() $v$ on
$v$ on ![]() $X$. Thus, we have
$X$. Thus, we have ![]() $n\geq 1$. From Proposition 4.4 applied to the composition
$n\geq 1$. From Proposition 4.4 applied to the composition ![]() $Y'\to Y \to X$ and
$Y'\to Y \to X$ and ![]() $v$, there is the following commutative diagram.
$v$, there is the following commutative diagram.

Let ![]() $w$ be the divisorial valuation on
$w$ be the divisorial valuation on ![]() $X$ corresponding to the penultimate exceptional divisor
$X$ corresponding to the penultimate exceptional divisor ![]() $E_{n-1}$ of the chain
$E_{n-1}$ of the chain ![]() $\mathbf {p}$. In particular, the centres of
$\mathbf {p}$. In particular, the centres of ![]() $v$ and
$v$ and ![]() $w$ on
$w$ on ![]() $X_{n-1}$ are
$X_{n-1}$ are ![]() $P_{n-1}$ and
$P_{n-1}$ and ![]() $E_{n-1}$, respectively. They are, in particular, distinct with that of
$E_{n-1}$, respectively. They are, in particular, distinct with that of ![]() $w$ being a divisor. Thus,
$w$ being a divisor. Thus, ![]() $E$ and the centre of
$E$ and the centre of ![]() $w$ on
$w$ on ![]() $Y'$ are distinct divisors. Since all what
$Y'$ are distinct divisors. Since all what ![]() $Y'\to Y$ does is to contract
$Y'\to Y$ does is to contract ![]() $E$ to
$E$ to ![]() $P$, we deduce that the centre of
$P$, we deduce that the centre of ![]() $w$ on
$w$ on ![]() $Y$ is again a divisor. A second application of Proposition 4.4 to
$Y$ is again a divisor. A second application of Proposition 4.4 to ![]() $f : Y\to X$ and
$f : Y\to X$ and ![]() $w$ yields the following commutative diagram.
$w$ yields the following commutative diagram.

Observe that the scheme ![]() $h^{-1}(P_{n-1})$ contains
$h^{-1}(P_{n-1})$ contains ![]() $P$. If
$P$. If ![]() $h^{-1}(P_{n-1})$ was an effective Cartier divisor, then the universal property of blow-up would provide the following commutative diagram.
$h^{-1}(P_{n-1})$ was an effective Cartier divisor, then the universal property of blow-up would provide the following commutative diagram.

In particular, the centre of ![]() $v$ on
$v$ on ![]() $Y$ would be a divisor. Contradiction. Hence,
$Y$ would be a divisor. Contradiction. Hence, ![]() $h^{-1}(P_{n-1})$ is not an effective Cartier divisor. From Lemma 4.3, we deduce the existence of a neighbourhood
$h^{-1}(P_{n-1})$ is not an effective Cartier divisor. From Lemma 4.3, we deduce the existence of a neighbourhood ![]() $U$ of
$U$ of ![]() $P_{n-1}$ in
$P_{n-1}$ in ![]() $X_{n-1}$ such that
$X_{n-1}$ such that ![]() $h$ induces an isomorphism
$h$ induces an isomorphism ![]() $h|_U : h^{-1}(U)\to U$ over
$h|_U : h^{-1}(U)\to U$ over ![]() $X$. Proposition 4.11 then follows.
$X$. Proposition 4.11 then follows.
Remark 4.12 The terminology partial discrepancy divisor comes from the fact that we are looking at the failure of ![]() $Z$ to lie in the image of
$Z$ to lie in the image of ![]() $\operatorname {Cart}(Y)\to \textbf {Div}(X)$ with
$\operatorname {Cart}(Y)\to \textbf {Div}(X)$ with ![]() $Y\to X$ a modification by only contemplating the smooth points of
$Y\to X$ a modification by only contemplating the smooth points of ![]() $Z(Y)$. The justification for this comes from Theorem 5.20, showing that de Rham cohomology only sees the partial discrepancy of the irregularity
$Z(Y)$. The justification for this comes from Theorem 5.20, showing that de Rham cohomology only sees the partial discrepancy of the irregularity ![]() $b$-divisors.
$b$-divisors.
Remark 4.13 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $f: Y \to X$ be a modification and put
$f: Y \to X$ be a modification and put ![]() $E:=(f^*D)_{red}$. Then, the canonical isomorphism
$E:=(f^*D)_{red}$. Then, the canonical isomorphism ![]() $\textbf {Div}(X)\to \textbf {Div}(Y)$ induces an isomorphism
$\textbf {Div}(X)\to \textbf {Div}(Y)$ induces an isomorphism ![]() $\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. We thus have the following square.
$\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. We thus have the following square.

We stress the fact that the above square does not commute. The lemma below asserts, however, that the only obstruction lies at valuations centred at divisors of ![]() $Y$.
$Y$.
Lemma 4.14 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $f: Y \to X$ be a modification over
$f: Y \to X$ be a modification over ![]() $k$ and put
$k$ and put ![]() $E:=(f^*D)_{red}$. Let
$E:=(f^*D)_{red}$. Let ![]() $Z$ be a
$Z$ be a ![]() $b$-divisor on
$b$-divisor on ![]() $(X,D)$ and let
$(X,D)$ and let ![]() $T$ be the image of
$T$ be the image of ![]() $Z$ under
$Z$ under ![]() $\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. Let
$\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. Let ![]() $v$ be a divisorial valuation on
$v$ be a divisorial valuation on ![]() $X$ centred at a closed point of
$X$ centred at a closed point of ![]() $Y$. Then,
$Y$. Then, ![]() $\delta Z$ and
$\delta Z$ and ![]() $\delta T$ coincide at
$\delta T$ coincide at ![]() $v$.
$v$.
Proof. We unveil the definition of ![]() $(\delta T)(v)$. Let
$(\delta T)(v)$. Let
be the chain of blow-up obtained by applying Theorem 4.2 to ![]() $Y$ and
$Y$ and ![]() $v$. By assumption on
$v$. By assumption on ![]() $v$, there is at least one blow-up, that is
$v$, there is at least one blow-up, that is ![]() $n\geq 1$. Let
$n\geq 1$. Let ![]() $Q$ be the last blow-up point. Let
$Q$ be the last blow-up point. Let ![]() $\rho : Y_{n-1}\to Y$ be the composition of the
$\rho : Y_{n-1}\to Y$ be the composition of the ![]() $q_i$,
$q_i$, ![]() $0\leq i\leq n-2$. If
$0\leq i\leq n-2$. If ![]() $Q$ is a singular point of
$Q$ is a singular point of ![]() $(\rho ^*E)_\mathrm {red} = (\rho ^* f^*D)_{\mathrm {red}}$, then by definition
$(\rho ^*E)_\mathrm {red} = (\rho ^* f^*D)_{\mathrm {red}}$, then by definition ![]() $(\delta T)(v)=0$. On the other hand, Proposition 4.11 applied to
$(\delta T)(v)=0$. On the other hand, Proposition 4.11 applied to ![]() $Z$,
$Z$, ![]() $v$ and
$v$ and ![]() $f \rho : Y_{n-1}\to X$ yields
$f \rho : Y_{n-1}\to X$ yields ![]() $(\delta Z)(v)=0$ so that
$(\delta Z)(v)=0$ so that ![]() $\delta Z$ and
$\delta Z$ and ![]() $\delta T$ coincide at
$\delta T$ coincide at ![]() $v$ in that case. Assume that
$v$ in that case. Assume that ![]() $Q$ is not a singular point of
$Q$ is not a singular point of ![]() $(\rho ^*E)_\mathrm {red} = (\rho ^* f^*D)_{\mathrm {red}}$. Then, by definition,
$(\rho ^*E)_\mathrm {red} = (\rho ^* f^*D)_{\mathrm {red}}$. Then, by definition, ![]() $(\delta T)(v)=(T(Y_{n-1}))(v)-T(v)$. On the other hand, Proposition 4.11 yields again
$(\delta T)(v)=(T(Y_{n-1}))(v)-T(v)$. On the other hand, Proposition 4.11 yields again ![]() $(\delta Z)(v)=(Z(Y_{n-1}))(v)-Z(v)$. Since
$(\delta Z)(v)=(Z(Y_{n-1}))(v)-Z(v)$. Since ![]() $Z(Y_{n-1})=T(Y_{n-1})$ and
$Z(Y_{n-1})=T(Y_{n-1})$ and ![]() $Z(v)=T(v)$, we conclude that
$Z(v)=T(v)$, we conclude that ![]() $\delta Z$ and
$\delta Z$ and ![]() $\delta T$ coincide at
$\delta T$ coincide at ![]() $v$ in that case. This concludes the proof of Lemma 4.14.
$v$ in that case. This concludes the proof of Lemma 4.14.
4.3 Integral of finitely supported  $b$-divisors
$b$-divisors
Let ![]() $X$ be a smooth connected surface over
$X$ be a smooth connected surface over ![]() $k$. Let
$k$. Let ![]() $f : Y\to X$ be a modification and let
$f : Y\to X$ be a modification and let ![]() $A \subset Y$ be a subset. Let
$A \subset Y$ be a subset. Let ![]() $\operatorname {ZR}^{\operatorname {divis}}(X,A)\subset \operatorname {ZR}^{\operatorname {divis}}(X)$ be the subset of divisorial valuations of
$\operatorname {ZR}^{\operatorname {divis}}(X,A)\subset \operatorname {ZR}^{\operatorname {divis}}(X)$ be the subset of divisorial valuations of ![]() $X$ whose centre on
$X$ whose centre on ![]() $Y$ is a point of
$Y$ is a point of ![]() $A$. For a
$A$. For a ![]() $b$-divisor
$b$-divisor ![]() $Z$ of
$Z$ of ![]() $X$ with finite support as a function on
$X$ with finite support as a function on ![]() $\operatorname {ZR}^{\operatorname {divis}}(X)$, we put
$\operatorname {ZR}^{\operatorname {divis}}(X)$, we put
 \[ \int_A Z := \sum_{v \in \operatorname{ZR}^{\operatorname{divis}}(X,A)} Z(v) \in \mathbb{Z}. \]
\[ \int_A Z := \sum_{v \in \operatorname{ZR}^{\operatorname{divis}}(X,A)} Z(v) \in \mathbb{Z}. \]
The goal of what follows is to prove that the partial discrepancy of a nef Cartier ![]() $b$-divisor is effective and finitely supported.
$b$-divisor is effective and finitely supported.
Proposition 4.15 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $Z$ be a Cartier
$Z$ be a Cartier ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$. Let
$(X,D)$. Let ![]() $f: Y\to X$ be a modification of
$f: Y\to X$ be a modification of ![]() $X$ such that
$X$ such that ![]() $Z$ lies in the image of
$Z$ lies in the image of ![]() $\operatorname {Cart}(Y)\to \textbf {Div}(X)$. Then,
$\operatorname {Cart}(Y)\to \textbf {Div}(X)$. Then, ![]() $\delta Z$ is supported on the set of divisorial valuations whose centre on
$\delta Z$ is supported on the set of divisorial valuations whose centre on ![]() $Y$ is an irreducible component of
$Y$ is an irreducible component of ![]() $f^*D$.
$f^*D$.
Proof. Put ![]() $E:=(f^*D)_{red}$. Let
$E:=(f^*D)_{red}$. Let ![]() $T$ be the image of
$T$ be the image of ![]() $Z$ under
$Z$ under ![]() $\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. By assumption,
$\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. By assumption, ![]() $T$ is a Cartier
$T$ is a Cartier ![]() $b$-divisor. Example 4.8 thus gives
$b$-divisor. Example 4.8 thus gives ![]() $\delta T=0$. From Lemma 4.14, we deduce that
$\delta T=0$. From Lemma 4.14, we deduce that ![]() $\delta Z$ vanishes at every divisorial valuation centred at a closed point of
$\delta Z$ vanishes at every divisorial valuation centred at a closed point of ![]() $Y$. This concludes the proof of Proposition 4.15.
$Y$. This concludes the proof of Proposition 4.15.
Proposition 4.16 Let ![]() $(X,D)$ be a connected pair of dimension
$(X,D)$ be a connected pair of dimension ![]() $2$ over
$2$ over ![]() $k$. Let
$k$. Let ![]() $Z$ be a Cartier
$Z$ be a Cartier ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$. Then,
$(X,D)$. Then, ![]() $\delta Z$ is a
$\delta Z$ is a ![]() $b$-divisor with finite support. In particular, the integral
$b$-divisor with finite support. In particular, the integral ![]() $\int _X \delta Z$ is a well-defined integer. If
$\int _X \delta Z$ is a well-defined integer. If ![]() $Z$ is furthermore nef,
$Z$ is furthermore nef, ![]() $\delta Z$ is effective. Hence,
$\delta Z$ is effective. Hence, ![]() $\int _X \delta Z$ is a positive integer.
$\int _X \delta Z$ is a positive integer.
Proof. That ![]() $\delta Z$ is a
$\delta Z$ is a ![]() $b$-divisor with finite support follows from Propositions 4.9 and 4.15. We are thus left to show that
$b$-divisor with finite support follows from Propositions 4.9 and 4.15. We are thus left to show that ![]() $\delta Z$ is effective if
$\delta Z$ is effective if ![]() $Z$ is nef. Let
$Z$ is nef. Let ![]() $v$ be a divisorial valuation on
$v$ be a divisorial valuation on ![]() $X$. Let
$X$. Let
be the chain of blow-up corresponding to ![]() $v$ via Theorem 4.2. Since
$v$ via Theorem 4.2. Since ![]() $Z$ is a nef Cartier divisor, we have
$Z$ is a nef Cartier divisor, we have ![]() $Z\leq Z(X_{n-1})$ in
$Z\leq Z(X_{n-1})$ in ![]() $\textbf {CDiv}(X)$ and Proposition 4.16 follows.
$\textbf {CDiv}(X)$ and Proposition 4.16 follows.
5. Formula for the characteristic cycle of connections on surfaces
5.1 Local Euler–Poincaré characteristic and characteristic cycle
Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $D_c^b(X(\mathbb {C}), \mathbb {C})$ be the derived category of sheaves of
$D_c^b(X(\mathbb {C}), \mathbb {C})$ be the derived category of sheaves of ![]() $\mathbb {C}$-vector spaces on
$\mathbb {C}$-vector spaces on ![]() $X(\mathbb {C})$ with bounded and constructible cohomology. For an object
$X(\mathbb {C})$ with bounded and constructible cohomology. For an object ![]() $K$ of
$K$ of ![]() $D_c^b(X(\mathbb {C}), \mathbb {C})$ and a point
$D_c^b(X(\mathbb {C}), \mathbb {C})$ and a point ![]() $x$ of
$x$ of ![]() $X(\mathbb {C})$, we put
$X(\mathbb {C})$, we put
We let ![]() $CC(K)$ be the characteristic cycle of
$CC(K)$ be the characteristic cycle of ![]() $K$. Let
$K$. Let ![]() $\mathbb {F}(X)$ be the group of
$\mathbb {F}(X)$ be the group of ![]() $\mathbb {Z}$-valued constructible functions on
$\mathbb {Z}$-valued constructible functions on ![]() $X(\mathbb {C})$. Let
$X(\mathbb {C})$. Let ![]() $L_X$ be the group of Lagrangian cycles of
$L_X$ be the group of Lagrangian cycles of ![]() $T^*X$ and let
$T^*X$ and let ![]() $\operatorname {Eu} : L_X \to \mathbb {F}(X)$ be the Euler morphism. The following theorem can be found in [Reference Kashiwara and SchapiraKS90, Th.9.7.11].
$\operatorname {Eu} : L_X \to \mathbb {F}(X)$ be the Euler morphism. The following theorem can be found in [Reference Kashiwara and SchapiraKS90, Th.9.7.11].
Theorem 5.1 The diagram

is commutative and its arrows are isomorphisms.
If ![]() $S$ is a constructible subset of
$S$ is a constructible subset of ![]() $X$, we denote by
$X$, we denote by ![]() $\mathbb {1}_S$ the function on
$\mathbb {1}_S$ the function on ![]() $X(\mathbb {C})$ which sends
$X(\mathbb {C})$ which sends ![]() $x\in S$ to
$x\in S$ to ![]() $1$ and
$1$ and ![]() $x\in X(\mathbb {C})\setminus S(\mathbb {C})$ to
$x\in X(\mathbb {C})\setminus S(\mathbb {C})$ to ![]() $0$. By construction, if
$0$. By construction, if ![]() $S$ is a smooth closed subvariety of
$S$ is a smooth closed subvariety of ![]() $X$, then
$X$, then ![]() $\operatorname {Eu}(T^*_S X)=(-1)^{\operatorname {codim} S}\mathbb {1}_S$.
$\operatorname {Eu}(T^*_S X)=(-1)^{\operatorname {codim} S}\mathbb {1}_S$.
We now define a cycle that will show up frequently in this paper.
Definition 5.2 Let ![]() $(X,D)$ be a simple normal crossing pair over
$(X,D)$ be a simple normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $D_1,\ldots, D_n$ be the irreducible components of
$D_1,\ldots, D_n$ be the irreducible components of ![]() $D$. Let
$D$. Let ![]() $R=\sum a_i D_i$ be an effective divisor supported on
$R=\sum a_i D_i$ be an effective divisor supported on ![]() $D$. For every
$D$. For every ![]() $I \subset \{ 1,\ldots, n\}$, set
$I \subset \{ 1,\ldots, n\}$, set
Define
 \[ LC(R) := {\sum_{I\subset \{ 1,\ldots, n\}}} \bigg(\displaystyle{\sum_{i\in I}} a_i \bigg)[T^*_{D_I}X]. \]
\[ LC(R) := {\sum_{I\subset \{ 1,\ldots, n\}}} \bigg(\displaystyle{\sum_{i\in I}} a_i \bigg)[T^*_{D_I}X]. \]
Remark 5.3 When ![]() $k=\mathbb {C}$ in the above definition,
$k=\mathbb {C}$ in the above definition, ![]() $LC(R)$ is the unique Lagrangian cycle in
$LC(R)$ is the unique Lagrangian cycle in ![]() $T^*X$ such that
$T^*X$ such that
 \[
\operatorname{Eu}(LC(R))=\begin{cases} -a_i & \text{if}\
x\in D_i^{\circ},\ i=1, \ldots, n, \\ 0 &
\text{otherwise.} \end{cases} \]
\[
\operatorname{Eu}(LC(R))=\begin{cases} -a_i & \text{if}\
x\in D_i^{\circ},\ i=1, \ldots, n, \\ 0 &
\text{otherwise.} \end{cases} \]
5.2 Characteristic cycle of a connection with good formal structure
The easy direction of the main theorem of [Reference TeyssierTey23] gives the following.
Lemma 5.4 Let ![]() $(X,D)$ be an analytic pair where
$(X,D)$ be an analytic pair where ![]() $D$ is smooth and connected. Let
$D$ is smooth and connected. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Assume that
$\operatorname {MIC}(X,D)$. Assume that ![]() $\mathcal {M}$ has good formal structure. Then
$\mathcal {M}$ has good formal structure. Then ![]() $\operatorname {Irr}_D^* \mathcal {M}$ is a local system of rank
$\operatorname {Irr}_D^* \mathcal {M}$ is a local system of rank ![]() $\operatorname {irr}(D,\mathcal {M})$ concentrated in degree
$\operatorname {irr}(D,\mathcal {M})$ concentrated in degree ![]() $1$.
$1$.
Proposition 5.5 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $D_1,\ldots, D_n$ be the irreducible components of
$D_1,\ldots, D_n$ be the irreducible components of ![]() $D$. Let
$D$. Let ![]() $\mathcal {M}$ be an objet of
$\mathcal {M}$ be an objet of ![]() $\operatorname {MIC}(X,D)$. Assume that
$\operatorname {MIC}(X,D)$. Assume that ![]() $\mathcal {M}$ has good formal structure. Then,
$\mathcal {M}$ has good formal structure. Then,
 \[ \chi(x, \operatorname{Sol}
\mathcal{M}^{\operatorname{an}})=\begin{cases}
\operatorname{rk} \mathcal{M} & \text{if}\ x\in X\setminus
D, \\ -\operatorname{irr}(D_i,\mathcal{M}) &
\text{if}\ x\in D_i^{\circ},\ i=1, \ldots, n, \\
0 & \text{otherwise.} \end{cases} \]
\[ \chi(x, \operatorname{Sol}
\mathcal{M}^{\operatorname{an}})=\begin{cases}
\operatorname{rk} \mathcal{M} & \text{if}\ x\in X\setminus
D, \\ -\operatorname{irr}(D_i,\mathcal{M}) &
\text{if}\ x\in D_i^{\circ},\ i=1, \ldots, n, \\
0 & \text{otherwise.} \end{cases} \]
Proof. The restriction of ![]() $\operatorname {Sol} \mathcal {M}^{\operatorname {an}}$ to the complement of
$\operatorname {Sol} \mathcal {M}^{\operatorname {an}}$ to the complement of ![]() $D$ is a local system concentrated in degree
$D$ is a local system concentrated in degree ![]() $0$. This gives the expected formula in that case. The case where
$0$. This gives the expected formula in that case. The case where ![]() $x$ lies in one of the
$x$ lies in one of the ![]() $D_i^{\circ }$ follows from Lemma 5.4. Let
$D_i^{\circ }$ follows from Lemma 5.4. Let ![]() $I\subset \{1,\ldots, n\}$ and suppose that
$I\subset \{1,\ldots, n\}$ and suppose that ![]() $I$ contains at least two elements. Let
$I$ contains at least two elements. Let ![]() $x$ be a point of
$x$ be a point of ![]() $D_I^{\circ }$. Let
$D_I^{\circ }$. Let ![]() $i\in I$ such that the number of irregular values of
$i\in I$ such that the number of irregular values of ![]() $\mathcal {M}$ at
$\mathcal {M}$ at ![]() $x$ having no pole along
$x$ having no pole along ![]() $D_i$ is maximal. Such an integer exists by goodness assumption on the irregular values. If
$D_i$ is maximal. Such an integer exists by goodness assumption on the irregular values. If ![]() $i_I : D_I \to X$ and
$i_I : D_I \to X$ and ![]() $j_i : D_i^{\circ } \to X$ are the inclusions, Corollary 3.4 of [Reference SabbahSab17] implies that the natural morphism
$j_i : D_i^{\circ } \to X$ are the inclusions, Corollary 3.4 of [Reference SabbahSab17] implies that the natural morphism
is an isomorphism. Hence, the germ of ![]() $\operatorname {Sol} \mathcal {M}^{\operatorname {an}}$ at
$\operatorname {Sol} \mathcal {M}^{\operatorname {an}}$ at ![]() $x$ is the cohomology complex of a local system of rank
$x$ is the cohomology complex of a local system of rank ![]() $\operatorname {irr}(D_i,\mathcal {M})$ on a torus of dimension
$\operatorname {irr}(D_i,\mathcal {M})$ on a torus of dimension ![]() $|I|-1>0$. Thus, we have
$|I|-1>0$. Thus, we have ![]() $\chi (x, \operatorname {Sol} \mathcal {M}^{\operatorname {an}})=0$ and this finishes the proof of Proposition 5.5.
$\chi (x, \operatorname {Sol} \mathcal {M}^{\operatorname {an}})=0$ and this finishes the proof of Proposition 5.5.
Proposition 5.6 Let ![]() $(X,D)$ be a simple normal crossing pair over
$(X,D)$ be a simple normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Assume that
$\operatorname {MIC}(X,D)$. Assume that ![]() $\mathcal {M}$ has good formal structure. Then,
$\mathcal {M}$ has good formal structure. Then,
with ![]() $CC(\mathcal {O}_X(\ast D))=\displaystyle {\sum _{I\subset \{ 1,\ldots, n\}}} [T^*_{D_I}X]$.
$CC(\mathcal {O}_X(\ast D))=\displaystyle {\sum _{I\subset \{ 1,\ldots, n\}}} [T^*_{D_I}X]$.
Proof. From Remark 1.6, we can suppose ![]() $k=\mathbb {C}$. Then, Proposition 5.6 follows from Proposition 5.5 after passing to the associated constructible functions.
$k=\mathbb {C}$. Then, Proposition 5.6 follows from Proposition 5.5 after passing to the associated constructible functions.
Remark 5.7 As pointed out by Budur, Xiao obtained in [Reference XiaoXia15, Theorem 1.4.1] a variant of Proposition 5.6 where the characteristic cycle is replaced by the log-characteristic cycle and where the good formal structure assumption is weakened into a cleanness assumption. For a proof of why good formal structure implies cleanness, see Theorems 3.2.11 and 3.3.12 in [Reference XiaoXia15, Theorem 1.4.1].
5.3 An application
Lemma 5.8 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ be objects of
$\mathcal {M}_2$ be objects of ![]() $\operatorname {MIC}(X,D)$. Then, the following statements are equivalent:
$\operatorname {MIC}(X,D)$. Then, the following statements are equivalent:
(i)
 $\operatorname {Irr} \mathcal {M}_1=\operatorname {Irr} \mathcal {M}_2$ in
$\operatorname {Irr} \mathcal {M}_1=\operatorname {Irr} \mathcal {M}_2$ in  $\textbf {Div}(X)$;
$\textbf {Div}(X)$;(ii) for every point
 $0$ of
$0$ of  $D$, for every locally closed smooth curve
$D$, for every locally closed smooth curve  $C \to X$ in
$C \to X$ in  $X$ meeting
$X$ meeting  $D$ at
$D$ at  $0$ only, we have
$0$ only, we have  $\operatorname {irr}(0,\mathcal {M}_1|_{C})=\operatorname {irr}(0,\mathcal {M}_2|_{C})$.
$\operatorname {irr}(0,\mathcal {M}_1|_{C})=\operatorname {irr}(0,\mathcal {M}_2|_{C})$.
Proof. Suppose that statement (i) holds. Let ![]() $C \to X$ be a locally closed smooth curve meeting
$C \to X$ be a locally closed smooth curve meeting ![]() $D$ at
$D$ at ![]() $0$ only. Let
$0$ only. Let ![]() $p : Y\to X$ be a resolution of the turning points of
$p : Y\to X$ be a resolution of the turning points of ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ as given by the Kedlaya–Mochizuki Theorem 1.32. By valuative criterion for properness, the immersion
$\mathcal {M}_2$ as given by the Kedlaya–Mochizuki Theorem 1.32. By valuative criterion for properness, the immersion ![]() $C\to X$ factors uniquely through an immersion
$C\to X$ factors uniquely through an immersion ![]() $C\to Y$ followed by
$C\to Y$ followed by ![]() $p$. At the cost of blowing-up further, we can suppose that
$p$. At the cost of blowing-up further, we can suppose that ![]() $C\to Y$ intersects
$C\to Y$ intersects ![]() $E:=f^{-1}(D)$ transversely at a point
$E:=f^{-1}(D)$ transversely at a point ![]() $0'$ of
$0'$ of ![]() $E^{\operatorname {sm}}$. Let
$E^{\operatorname {sm}}$. Let ![]() $Z$ be the component of
$Z$ be the component of ![]() $E$ containing
$E$ containing ![]() $0'$. Then
$0'$. Then
Suppose that statement (ii) holds. Let ![]() $p : Y\to X$ be a modification and let
$p : Y\to X$ be a modification and let ![]() $Z$ be an irreducible component of
$Z$ be an irreducible component of ![]() $p^{-1}(D)$. Let
$p^{-1}(D)$. Let ![]() $0'$ be a point of
$0'$ be a point of ![]() $Z^{\operatorname {sm}}$ such that
$Z^{\operatorname {sm}}$ such that ![]() $p^+\mathcal {M}_1$ and
$p^+\mathcal {M}_1$ and ![]() $p^+\mathcal {M}_2$ have good formal decomposition at
$p^+\mathcal {M}_2$ have good formal decomposition at ![]() $0'$. Put
$0'$. Put ![]() $0:=p(0')$. Let
$0:=p(0')$. Let ![]() $C\to Y$ be a locally closed smooth curve meeting
$C\to Y$ be a locally closed smooth curve meeting ![]() $p^{-1}(D)$ transversely at
$p^{-1}(D)$ transversely at ![]() $0'$ only. Let
$0'$ only. Let ![]() $C\to X$ be the induced locally closed smooth curve of
$C\to X$ be the induced locally closed smooth curve of ![]() $X$. Then
$X$. Then
and the proof of Lemma 5.8 is complete.
Proposition 5.9 Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ be objects of
$\mathcal {M}_2$ be objects of ![]() $\operatorname {MIC}(X,D)$ with the same rank. Suppose that for every point
$\operatorname {MIC}(X,D)$ with the same rank. Suppose that for every point ![]() $0$ of
$0$ of ![]() $D$, for every locally closed smooth curve
$D$, for every locally closed smooth curve ![]() $C \to X$ in
$C \to X$ in ![]() $X$ meeting
$X$ meeting ![]() $D$ at
$D$ at ![]() $0$ only, we have
$0$ only, we have
Then ![]() $CC(\mathcal {M}_1)=CC(\mathcal {M}_2)$.
$CC(\mathcal {M}_1)=CC(\mathcal {M}_2)$.
Proof. From Remark 1.6, we can suppose that ![]() $k=\mathbb {C}$. From the Kedlaya–Mochizuki Theorem 1.32 combined with Lemmas 3.17 and 1.18, we can suppose that
$k=\mathbb {C}$. From the Kedlaya–Mochizuki Theorem 1.32 combined with Lemmas 3.17 and 1.18, we can suppose that ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ have good formal structure and that
$\mathcal {M}_2$ have good formal structure and that ![]() $D$ has simple normal crossings. From Lemma 5.8, we have
$D$ has simple normal crossings. From Lemma 5.8, we have ![]() $\operatorname {Irr}(X,\mathcal {M}_1)=\operatorname {Irr}(X,\mathcal {M}_2)$. Hence, Proposition 5.9 follows from Proposition 5.6.
$\operatorname {Irr}(X,\mathcal {M}_1)=\operatorname {Irr}(X,\mathcal {M}_2)$. Hence, Proposition 5.9 follows from Proposition 5.6.
Remark 5.10 In the étale setting, Proposition 5.9 is a theorem of Kato [Reference KatoKat21].
5.4 Partial discrepancy of the irregularity divisor
Applying the partial discrepancy construction to the irregularity ![]() $b$-divisor, § 4 can be summarized by the following proposition.
$b$-divisor, § 4 can be summarized by the following proposition.
Proposition 5.11 Let ![]() $(X,D)$ be a normal crossing connected surface over
$(X,D)$ be a normal crossing connected surface over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then,
$\operatorname {MIC}(X,D)$. Then, ![]() $\delta \operatorname {Irr}\mathcal {M}$ is an effective
$\delta \operatorname {Irr}\mathcal {M}$ is an effective ![]() $b$-divisor of
$b$-divisor of ![]() $(X,D)$ with finite support. In particular,
$(X,D)$ with finite support. In particular, ![]() $\int _X \delta \operatorname {Irr}\mathcal {M}$ is a well-defined positive integer.
$\int _X \delta \operatorname {Irr}\mathcal {M}$ is a well-defined positive integer.
Proof. From Kedlaya's Theorem 1.44, the ![]() $b$-divisor
$b$-divisor ![]() $\operatorname {Irr}\mathcal {M}$ is nef and Cartier. Then, Proposition 5.11 follows from Proposition 4.16.
$\operatorname {Irr}\mathcal {M}$ is nef and Cartier. Then, Proposition 5.11 follows from Proposition 4.16.
The non-trivial contributions to the above integral are located above the turning points. This is the content of the following.
Lemma 5.12 Let ![]() $(X,D)$ be a connected normal crossing surface over
$(X,D)$ be a connected normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$ and let
$\operatorname {MIC}(X,D)$ and let ![]() $V(\mathcal {M})$ be the complement of
$V(\mathcal {M})$ be the complement of ![]() $\operatorname {TL}(\mathcal {M})$. Then, the restriction of
$\operatorname {TL}(\mathcal {M})$. Then, the restriction of ![]() $\delta \operatorname {Irr} \mathcal {M}$ to
$\delta \operatorname {Irr} \mathcal {M}$ to ![]() $\operatorname {ZR}^{\operatorname {divis}}(V(\mathcal {M}))$ is
$\operatorname {ZR}^{\operatorname {divis}}(V(\mathcal {M}))$ is ![]() $0$. In particular, for every subset
$0$. In particular, for every subset ![]() $A\subset X$, we have
$A\subset X$, we have
Proof. We know that ![]() $\mathcal {M}|_{V(\mathcal {M})}$ has good formal decomposition. Thus,
$\mathcal {M}|_{V(\mathcal {M})}$ has good formal decomposition. Thus, ![]() $(\operatorname {Irr} \mathcal {M})|_{\operatorname {ZR}^{\operatorname {divis}}(V(\mathcal {M}))}=\operatorname {Irr} \mathcal {M}|_{V(\mathcal {M})}$ lies in the image of
$(\operatorname {Irr} \mathcal {M})|_{\operatorname {ZR}^{\operatorname {divis}}(V(\mathcal {M}))}=\operatorname {Irr} \mathcal {M}|_{V(\mathcal {M})}$ lies in the image of ![]() $\operatorname {Cart}(X)\to \textbf {Div}(X)$. Lemma 5.12 then follows from Example 4.8.
$\operatorname {Cart}(X)\to \textbf {Div}(X)$. Lemma 5.12 then follows from Example 4.8.
5.5 Local Euler–Poincaré characteristic and partial discrepancy divisor
Lemma 5.13 Let ![]() $(X,D)$ be a normal crossing connected surface over
$(X,D)$ be a normal crossing connected surface over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $q : Y\to X$ be a modification. Let
$q : Y\to X$ be a modification. Let ![]() $Q$ be a closed point of
$Q$ be a closed point of ![]() $Y$. Then,
$Y$. Then, ![]() $\delta \operatorname {Irr}\mathcal {M}$ and
$\delta \operatorname {Irr}\mathcal {M}$ and ![]() $\delta \operatorname {Irr} q^+\mathcal {M}$ coincide at every valuation of
$\delta \operatorname {Irr} q^+\mathcal {M}$ coincide at every valuation of ![]() $X$ centred at
$X$ centred at ![]() $Q$. In particular,
$Q$. In particular,
Proof. Put ![]() $E:=(q^*D)_{red}$. Then,
$E:=(q^*D)_{red}$. Then, ![]() $\operatorname {Irr} q^+\mathcal {M}$ is the image of
$\operatorname {Irr} q^+\mathcal {M}$ is the image of ![]() $\operatorname {Irr}\mathcal {M}$ under
$\operatorname {Irr}\mathcal {M}$ under ![]() $\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. Thus, Lemma 5.13 follows from Lemma 4.14.
$\textbf {Div}(X,D)\to \textbf {Div}(Y,E)$. Thus, Lemma 5.13 follows from Lemma 4.14.
Theorem 5.14 Let ![]() $(X,D)$ be a normal crossing surface over
$(X,D)$ be a normal crossing surface over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $P$ be a closed point of
$P$ be a closed point of ![]() $D$. If
$D$. If ![]() $P$ is a singular point of
$P$ is a singular point of ![]() $D$, we have
$D$, we have
Otherwise, we have
where ![]() $Z$ is the component of
$Z$ is the component of ![]() $D$ containing
$D$ containing ![]() $P$.
$P$.
Proof. We argue by recursion on the number of blow-ups needed to resolve the turning points of ![]() $\mathcal {M}$ lying above
$\mathcal {M}$ lying above ![]() $P$. If no blow-up is needed, this means that
$P$. If no blow-up is needed, this means that ![]() $\mathcal {M}$ has good formal structure in a neighbourhood of
$\mathcal {M}$ has good formal structure in a neighbourhood of ![]() $P$. Then, Theorem 1.47 ensures that
$P$. Then, Theorem 1.47 ensures that ![]() $\operatorname {Irr}\mathcal {M}$ lies in the image of
$\operatorname {Irr}\mathcal {M}$ lies in the image of ![]() $\operatorname {Cart}(X)\to \textbf {Div}(X)$. Hence, Example 4.8 yields
$\operatorname {Cart}(X)\to \textbf {Div}(X)$. Hence, Example 4.8 yields ![]() $\delta \operatorname {Irr} \mathcal {M}=0$. Theorem 5.14 then follows from Proposition 5.5.
$\delta \operatorname {Irr} \mathcal {M}=0$. Theorem 5.14 then follows from Proposition 5.5.
Let ![]() $n>0$. Let
$n>0$. Let ![]() $p : Y\to X$ be a sequence of blow-up of length
$p : Y\to X$ be a sequence of blow-up of length ![]() $n$ above
$n$ above ![]() $P$ such that
$P$ such that ![]() $p^+\mathcal {M}$ has good formal structure in a neighbourhood of
$p^+\mathcal {M}$ has good formal structure in a neighbourhood of ![]() $p^{-1}(P)$. Then,
$p^{-1}(P)$. Then, ![]() $p=f\circ q$ where
$p=f\circ q$ where ![]() $q : X_1\to X$ is the blow-up at
$q : X_1\to X$ is the blow-up at ![]() $P$ and where
$P$ and where ![]() $f:Y\to X_1$ is a sequence of
$f:Y\to X_1$ is a sequence of ![]() $(n-1)$-blow-up above
$(n-1)$-blow-up above ![]() $P$. Let
$P$. Let ![]() $E$ be the exceptional divisor of
$E$ be the exceptional divisor of ![]() $q$. Let
$q$. Let ![]() $D'$ be the strict transform of
$D'$ be the strict transform of ![]() $D$. Let
$D$. Let ![]() $S$ be the set of points of
$S$ be the set of points of ![]() $E$ which are either turning points for
$E$ which are either turning points for ![]() $q^+\mathcal {M}$ or points of
$q^+\mathcal {M}$ or points of ![]() $E\cap D'$. Put
$E\cap D'$. Put ![]() $U=E\setminus S$ and let
$U=E\setminus S$ and let ![]() $j : U\to E$ and
$j : U\to E$ and ![]() $i : S\to E$ be the inclusions. The localization triangle for
$i : S\to E$ be the inclusions. The localization triangle for ![]() $(\operatorname {Sol} q^+\mathcal {M}^{\operatorname {an}})|_{E}$ reads as follows:
$(\operatorname {Sol} q^+\mathcal {M}^{\operatorname {an}})|_{E}$ reads as follows:
From Lemma 3.17 and the compatibility of ![]() $\operatorname {Sol}$ with proper push-forward, we deduce
$\operatorname {Sol}$ with proper push-forward, we deduce
Since ![]() $(\operatorname {Sol} q^+\mathcal {M}^{\operatorname {an}})|_{U}$ is a local system of rank
$(\operatorname {Sol} q^+\mathcal {M}^{\operatorname {an}})|_{U}$ is a local system of rank ![]() $\operatorname {irr}(E,q^+\mathcal {M})$ on
$\operatorname {irr}(E,q^+\mathcal {M})$ on ![]() $U$ concentrated in degree
$U$ concentrated in degree ![]() $1$, we have
$1$, we have
For a turning point ![]() $Q\in E$ for
$Q\in E$ for ![]() $q^+\mathcal {M}$ not in
$q^+\mathcal {M}$ not in ![]() $D'$, the recursion hypothesis gives
$D'$, the recursion hypothesis gives
 \begin{align*} \chi(Q, \operatorname{Sol} q^+ \mathcal{M}^{\operatorname{an}})& =-\operatorname{irr}(E, q^+ \mathcal{M})+\int_{Q} \delta \operatorname{Irr} q^+\mathcal{M} \\ & =-\operatorname{irr}(E, q^+ \mathcal{M})+\int_{Q} \delta \operatorname{Irr} \mathcal{M}, \end{align*}
\begin{align*} \chi(Q, \operatorname{Sol} q^+ \mathcal{M}^{\operatorname{an}})& =-\operatorname{irr}(E, q^+ \mathcal{M})+\int_{Q} \delta \operatorname{Irr} q^+\mathcal{M} \\ & =-\operatorname{irr}(E, q^+ \mathcal{M})+\int_{Q} \delta \operatorname{Irr} \mathcal{M}, \end{align*}
where the second equality follows from Lemma 5.13. For a point ![]() $Q$ in
$Q$ in ![]() $E\cap D'$, the recursion hypothesis gives
$E\cap D'$, the recursion hypothesis gives
where the second equality again follows from Lemma 5.13. Let ![]() $\operatorname {nb}_D(P)$ be the number of local branches of
$\operatorname {nb}_D(P)$ be the number of local branches of ![]() $D$ around
$D$ around ![]() $P$ passing through
$P$ passing through ![]() $P$. Note that
$P$. Note that ![]() $\operatorname {nb}_D(P)$ is equal to the cardinality of
$\operatorname {nb}_D(P)$ is equal to the cardinality of ![]() $E\cap D'$. Putting the above equalities together yields
$E\cap D'$. Putting the above equalities together yields
Let ![]() $v$ be the valuation of
$v$ be the valuation of ![]() $X$ corresponding to
$X$ corresponding to ![]() $E$, so that
$E$, so that
If ![]() $P$ is a singular point of
$P$ is a singular point of ![]() $D$, then
$D$, then ![]() $\operatorname {nb}_D(P) =2$ and
$\operatorname {nb}_D(P) =2$ and ![]() $(\delta \operatorname {Irr} \mathcal {M})(v)=0$. Thus, Theorem 5.14 is true in that case. Otherwise, let
$(\delta \operatorname {Irr} \mathcal {M})(v)=0$. Thus, Theorem 5.14 is true in that case. Otherwise, let ![]() $Z$ be the unique irreducible component of
$Z$ be the unique irreducible component of ![]() $D$ passing through
$D$ passing through ![]() $P$. Then,
$P$. Then, ![]() $\operatorname {nb}_D(P)=1$ and
$\operatorname {nb}_D(P)=1$ and ![]() $(\delta \operatorname {Irr} \mathcal {M})(v)=\operatorname {irr}(Z,\mathcal {M})-\operatorname {irr}(E,q^+\mathcal {M})$. Hence, Theorem 5.14 is again true in that case. This finishes the proof of Theorem 5.14.
$(\delta \operatorname {Irr} \mathcal {M})(v)=\operatorname {irr}(Z,\mathcal {M})-\operatorname {irr}(E,q^+\mathcal {M})$. Hence, Theorem 5.14 is again true in that case. This finishes the proof of Theorem 5.14.
Corollary 5.17 Let ![]() $(X,D)$ be a normal crossing surface over an algebraically closed field of characteristic
$(X,D)$ be a normal crossing surface over an algebraically closed field of characteristic ![]() $0$. Let
$0$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $P$ be a closed point of
$P$ be a closed point of ![]() $D$. If
$D$. If ![]() $P$ lies in the smooth locus of
$P$ lies in the smooth locus of ![]() $D$, the multiplicity of
$D$, the multiplicity of ![]() $T_P^*X$ in
$T_P^*X$ in ![]() $CC(\mathcal {M})$ is
$CC(\mathcal {M})$ is
If ![]() $P$ lies in two irreducible components
$P$ lies in two irreducible components ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ of
$Z_2$ of ![]() $D$, the multiplicity of
$D$, the multiplicity of ![]() $T_P^*X$ in
$T_P^*X$ in ![]() $CC(\mathcal {M})$ is
$CC(\mathcal {M})$ is
Proof. From Remark 1.6 and Lemma A.6, we can suppose that the base field is ![]() $\mathbb {C}$. Suppose that
$\mathbb {C}$. Suppose that ![]() $P$ lies in
$P$ lies in ![]() $D^{\operatorname {sm}}$. Then, at the cost of shrinking
$D^{\operatorname {sm}}$. Then, at the cost of shrinking ![]() $X$, we can suppose that
$X$, we can suppose that ![]() $D$ is smooth and that
$D$ is smooth and that ![]() $T_Q^*X$ does not contribute to
$T_Q^*X$ does not contribute to ![]() $CC(\mathcal {M})$ for
$CC(\mathcal {M})$ for ![]() $Q\neq P$. Thus, we have
$Q\neq P$. Thus, we have
where ![]() $m$ is the sought-after multiplicity. Applying Theorem 1.15 and passing to the associated constructible functions yields
$m$ is the sought-after multiplicity. Applying Theorem 1.15 and passing to the associated constructible functions yields
From Theorem 5.14, evaluating at ![]() $P$ then gives
$P$ then gives ![]() $m= \int _{P} \delta \operatorname {Irr}\mathcal {M}$.
$m= \int _{P} \delta \operatorname {Irr}\mathcal {M}$.
Suppose that ![]() $P$ lies in two irreducible components
$P$ lies in two irreducible components ![]() $Z_1$ and
$Z_1$ and ![]() $Z_2$ of
$Z_2$ of ![]() $D$. At the cost of shrinking
$D$. At the cost of shrinking ![]() $X$, we have
$X$, we have
where ![]() $m$ is the sought-after multiplicity. Applying Theorem 1.15 and passing to the associated constructible functions yields
$m$ is the sought-after multiplicity. Applying Theorem 1.15 and passing to the associated constructible functions yields
From Theorem 5.14, evaluating at ![]() $P$ gives the expected formula.
$P$ gives the expected formula.
Putting together Proposition 5.6 and Corollary 5.17 yields the following.
Theorem 5.18 Let ![]() $(X,D)$ be a simple normal crossing surface over an algebraically closed field of characteristic
$(X,D)$ be a simple normal crossing surface over an algebraically closed field of characteristic ![]() $0$. Let
$0$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then
$\operatorname {MIC}(X,D)$. Then
 \[ CC(\mathcal{M}) = \operatorname{rk} \mathcal{M} \cdot CC(\mathcal{O}_{X}(\ast D)) + LC(\operatorname{Irr}(X,\mathcal{M})) + \sum_{P\in D} \bigg( \int_{P} \delta\operatorname{Irr}\mathcal{M}\bigg) \cdot T_{P}^*X. \]
\[ CC(\mathcal{M}) = \operatorname{rk} \mathcal{M} \cdot CC(\mathcal{O}_{X}(\ast D)) + LC(\operatorname{Irr}(X,\mathcal{M})) + \sum_{P\in D} \bigg( \int_{P} \delta\operatorname{Irr}\mathcal{M}\bigg) \cdot T_{P}^*X. \]
Remark 5.19 In the étale setting, Yatagawa obtained an explicit description of the characteristic cycle for rank-one étale sheaves on surfaces [Reference YatagawaYat20]. It seems an interesting question to connect Yatagawa's work to the étale analogue of the irregularity ![]() $b$-divisor.
$b$-divisor.
In the complex setting, Kashiwara and Dubson's formula stated in Theorem 1.17 yields the following Grothendieck–Ogg Shafarevich-type formula for surfaces.
Theorem 5.20 Let ![]() $(X,D)$ be a proper simple normal crossing surface over
$(X,D)$ be a proper simple normal crossing surface over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Put
$\operatorname {MIC}(X,D)$. Put ![]() $U:=X\setminus D$. Then
$U:=X\setminus D$. Then
6. Cohomological boundedness
6.1 Cohomological boundedness for surfaces
Lemma 6.1 Let ![]() $(X,D)$ be a proper simple normal crossing surface over
$(X,D)$ be a proper simple normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $V$ be an open subset of
$V$ be an open subset of ![]() $X$ such that
$X$ such that ![]() $D_V:=V\cap D$ is the vanishing locus of an algebraic function
$D_V:=V\cap D$ is the vanishing locus of an algebraic function ![]() $f : V\to \mathbb {A}^1$. Then, there exists a commutative diagram of smooth varieties over
$f : V\to \mathbb {A}^1$. Then, there exists a commutative diagram of smooth varieties over ![]() $k$
$k$

satisfying the following conditions.
(i) The map
 $j : V\to Y$ is a dense open immersion.
$j : V\to Y$ is a dense open immersion.(ii) The map
 $h$ is proper and dominant.
$h$ is proper and dominant.(iii) If
 $E:=((Y\setminus V)\cup h^{-1}(0))_{\mathrm {red}}$, the pair
$E:=((Y\setminus V)\cup h^{-1}(0))_{\mathrm {red}}$, the pair  $(Y,E)$ is a simple normal crossing surface with
$(Y,E)$ is a simple normal crossing surface with  $Y\setminus E=V\setminus D_V$.
$Y\setminus E=V\setminus D_V$.(iv) For every effective divisor
 $R$ supported on
$R$ supported on  $D$, there exists an effective divisor
$D$, there exists an effective divisor  $S$ supported on
$S$ supported on  $E$ depending only on
$E$ depending only on  $V$, on
$V$, on  $j : (V,D_V) \to (Y,E)$ and linearly on
$j : (V,D_V) \to (Y,E)$ and linearly on  $R$ such that for every object
$R$ such that for every object  $\mathcal {M}$ of
$\mathcal {M}$ of  $\operatorname {MIC}(X,D,R)$, the connection
$\operatorname {MIC}(X,D,R)$, the connection  $j_* \mathcal {M}|_V$ is an object of
$j_* \mathcal {M}|_V$ is an object of  $\operatorname {MIC}(Y,E,S)$.
$\operatorname {MIC}(Y,E,S)$.
Proof. By Nagata compactification theorem applied to the composition ![]() $V\to \mathbb {P}^1$, there exists a commutative diagram (6.2) where
$V\to \mathbb {P}^1$, there exists a commutative diagram (6.2) where ![]() $j : V\to Y$ is a dense open immersion with
$j : V\to Y$ is a dense open immersion with ![]() $Y$ a variety over
$Y$ a variety over ![]() $k$ and where
$k$ and where ![]() $h$ is proper. Observe that
$h$ is proper. Observe that ![]() $h$ is dominant because
$h$ is dominant because ![]() $f$ is dominant. By normalizing and blowing-up enough points above the singular locus
$f$ is dominant. By normalizing and blowing-up enough points above the singular locus ![]() $Y^{\operatorname {sing}} \subset Y\setminus V$, resolution of singularities for surfaces ensures that we can suppose
$Y^{\operatorname {sing}} \subset Y\setminus V$, resolution of singularities for surfaces ensures that we can suppose ![]() $Y$ to be smooth. Put
$Y$ to be smooth. Put ![]() $E:=((Y\setminus V)\cup h^{-1}(0))_{\mathrm {red}}$. Then the equality
$E:=((Y\setminus V)\cup h^{-1}(0))_{\mathrm {red}}$. Then the equality ![]() $Y\setminus E=V\setminus D_V$ is automatic. Furthermore,
$Y\setminus E=V\setminus D_V$ is automatic. Furthermore, ![]() $E\cap V = h^{-1}(0)\cap V =D_V$ is a simple normal crossing divisor of
$E\cap V = h^{-1}(0)\cap V =D_V$ is a simple normal crossing divisor of ![]() $V$. Hence, at the cost of blowing-up enough points above
$V$. Hence, at the cost of blowing-up enough points above ![]() $E\setminus E\cap V$, we can further suppose that
$E\setminus E\cap V$, we can further suppose that ![]() $E$ is a simple normal crossing divisor of
$E$ is a simple normal crossing divisor of ![]() $Y$. Conditions (i)–(iii) are thus satisfied. Since
$Y$. Conditions (i)–(iii) are thus satisfied. Since ![]() $h$ and
$h$ and ![]() $\mathbb {P}^1$ are proper, so is
$\mathbb {P}^1$ are proper, so is ![]() $Y$. Hence, condition (iv) is satisfied as a consequence of Proposition 3.7 and the proof of Lemma 6.1 is complete.
$Y$. Hence, condition (iv) is satisfied as a consequence of Proposition 3.7 and the proof of Lemma 6.1 is complete.
Lemma 6.3 Let ![]() $(X,D)$ be a simple normal crossing surface over
$(X,D)$ be a simple normal crossing surface over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $Z$ be a reduced divisor of
$Z$ be a reduced divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. For a smooth point
$D$. For a smooth point ![]() $P$ of
$P$ of ![]() $Z$ which is singular in
$Z$ which is singular in ![]() $D$, let
$D$, let ![]() $Z(P)$ be the component of
$Z(P)$ be the component of ![]() $Z$ containing
$Z$ containing ![]() $P$. Let
$P$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $\operatorname {Irr}(X,Z,\mathcal {M})$ be the effective divisor supported on
$\operatorname {Irr}(X,Z,\mathcal {M})$ be the effective divisor supported on ![]() $Z$ which coincides with
$Z$ which coincides with ![]() $\operatorname {Irr}(X,\mathcal {M})$ on
$\operatorname {Irr}(X,\mathcal {M})$ on ![]() $Z$. Then,
$Z$. Then,
 \begin{align*} CC((\operatorname{Sol} \mathcal{M}^{\operatorname{an}})|_{Z(\mathbb{C})}) & = LC(\operatorname{Irr}(X,Z,\mathcal{M})) + \sum_{P\in Z} \bigg( \int_{P} \delta\operatorname{Irr}\mathcal{M}\bigg) \cdot T_{P}^*X \\ & \quad+ \sum_{P\in Z^{\operatorname{sm}}\cap D^{\operatorname{sing}}} \operatorname{irr}(Z(P),\mathcal{M}) \cdot T_{P}^*X, \end{align*}
\begin{align*} CC((\operatorname{Sol} \mathcal{M}^{\operatorname{an}})|_{Z(\mathbb{C})}) & = LC(\operatorname{Irr}(X,Z,\mathcal{M})) + \sum_{P\in Z} \bigg( \int_{P} \delta\operatorname{Irr}\mathcal{M}\bigg) \cdot T_{P}^*X \\ & \quad+ \sum_{P\in Z^{\operatorname{sm}}\cap D^{\operatorname{sing}}} \operatorname{irr}(Z(P),\mathcal{M}) \cdot T_{P}^*X, \end{align*}
where ![]() $(\operatorname {Sol} \mathcal {M}^{\operatorname {an}})|_{Z(\mathbb {C})}$ is viewed as a complex of sheaves on
$(\operatorname {Sol} \mathcal {M}^{\operatorname {an}})|_{Z(\mathbb {C})}$ is viewed as a complex of sheaves on ![]() $X$ supported on
$X$ supported on ![]() $Z(\mathbb {C})$.
$Z(\mathbb {C})$.
Proof. We conclude via Theorem 5.14 by looking at the associated constructible functions.
Proposition 6.4 Let ![]() $(X,D)$ be a geometrically connected simple normal crossing surface over
$(X,D)$ be a geometrically connected simple normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $C$ be a smooth connected curve over
$C$ be a smooth connected curve over ![]() $k$. Let
$k$. Let ![]() $h : X\to C$ be a dominant proper morphism. Let
$h : X\to C$ be a dominant proper morphism. Let ![]() $0$ be a closed point in
$0$ be a closed point in ![]() $C$. Suppose that the reduced fibre
$C$. Suppose that the reduced fibre ![]() $Z$ of
$Z$ of ![]() $h$ over
$h$ over ![]() $0$ is not empty and is contained in
$0$ is not empty and is contained in ![]() $D$. Then, there exists a quadratic polynomial
$D$. Then, there exists a quadratic polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
Proof. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $r$ be an integer. Let
$r$ be an integer. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}_r(X,D,R)$. From Lemma A.4, we can suppose that
$\operatorname {MIC}_r(X,D,R)$. From Lemma A.4, we can suppose that ![]() $k$ is algebraically closed. From Lemma A.8, we can suppose that
$k$ is algebraically closed. From Lemma A.8, we can suppose that ![]() $k=\mathbb {C}$. The turning locus of
$k=\mathbb {C}$. The turning locus of ![]() $\mathcal {M}$ consists in a finite set of closed points in
$\mathcal {M}$ consists in a finite set of closed points in ![]() $D$. At the cost of shrinking
$D$. At the cost of shrinking ![]() $C$, we can thus suppose
$C$, we can thus suppose ![]() $\operatorname {TL}(\mathcal {M})\subset Z$. On the other hand, Lemma 2.9 ensures that cohomological boundedness holds with bound
$\operatorname {TL}(\mathcal {M})\subset Z$. On the other hand, Lemma 2.9 ensures that cohomological boundedness holds with bound ![]() $K_1$ for the generic fibre of
$K_1$ for the generic fibre of ![]() $h : X\to C$. Note that
$h : X\to C$. Note that ![]() $K_1$ is an affine map. Hence, Proposition 3.23 implies
$K_1$ is an affine map. Hence, Proposition 3.23 implies
where ![]() $R_\eta$ is the pull-back of
$R_\eta$ is the pull-back of ![]() $R$ to the generic fibre of
$R$ to the generic fibre of ![]() $h : X\to C$. Since
$h : X\to C$. Since ![]() $h$ is proper, the complex manifold
$h$ is proper, the complex manifold ![]() $Z(\mathbb {C})$ is compact. Hence, the index formula for constructible sheaves [Reference KashiwaraKas85, Theorem 4.3] yields
$Z(\mathbb {C})$ is compact. Hence, the index formula for constructible sheaves [Reference KashiwaraKas85, Theorem 4.3] yields
 \begin{align*} \chi(Z(\mathbb{C}),\operatorname{Sol} \mathcal{M}^{\operatorname{an}}) & = (CC((\operatorname{Sol} \mathcal{M}^{\operatorname{an}})|_{Z(\mathbb{C})}),T^*_X X)_{T^*X} \\ & = (LC(\operatorname{Irr}(X,Z,\mathcal{M})),T^*_X X)_{T^*X} + \int_{Z} \delta\operatorname{Irr}\mathcal{M} \\ & \quad + \sum_{P\in Z^{\operatorname{sm}}\cap D^{\operatorname{sing}}} \operatorname{irr}(Z(P),\mathcal{M}), \end{align*}
\begin{align*} \chi(Z(\mathbb{C}),\operatorname{Sol} \mathcal{M}^{\operatorname{an}}) & = (CC((\operatorname{Sol} \mathcal{M}^{\operatorname{an}})|_{Z(\mathbb{C})}),T^*_X X)_{T^*X} \\ & = (LC(\operatorname{Irr}(X,Z,\mathcal{M})),T^*_X X)_{T^*X} + \int_{Z} \delta\operatorname{Irr}\mathcal{M} \\ & \quad + \sum_{P\in Z^{\operatorname{sm}}\cap D^{\operatorname{sing}}} \operatorname{irr}(Z(P),\mathcal{M}), \end{align*}
where the second equality follows from Lemma 6.3. Hence, we have
Let ![]() $Z_1,\ldots, Z_n$ be the irreducible components of
$Z_1,\ldots, Z_n$ be the irreducible components of ![]() $Z$. Then
$Z$. Then
 \[ |(LC(\operatorname{Irr}(X,Z,\mathcal{M})),T^*_X X)_{T^*X} |\leq \sum_{i=1}^n m(Z_i,R) |(Z_i,T^*_X X)_{T^*X}|. \]
\[ |(LC(\operatorname{Irr}(X,Z,\mathcal{M})),T^*_X X)_{T^*X} |\leq \sum_{i=1}^n m(Z_i,R) |(Z_i,T^*_X X)_{T^*X}|. \]
If ![]() $K_2(R)$ denotes the right-hand side of the above inequality, we have
$K_2(R)$ denotes the right-hand side of the above inequality, we have
and the proof of Proposition 6.4 is complete.
Putting everything together yields the following absolute version of Proposition 6.4.
Theorem 6.5 Let ![]() $(X,D)$ be a geometrically connected proper simple normal crossing surface over
$(X,D)$ be a geometrically connected proper simple normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $Z$ be a subset of
$Z$ be a subset of ![]() $D$. Then, there exists a quadratic polynomial
$D$. Then, there exists a quadratic polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
Proof. Let ![]() $R$ be an effective divisor supported on
$R$ be an effective divisor supported on ![]() $D$. Let
$D$. Let ![]() $r$ be an integer. Let
$r$ be an integer. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}_r(X,D,R)$. Let
$\operatorname {MIC}_r(X,D,R)$. Let ![]() $\mathcal {V}$ be a finite cover of
$\mathcal {V}$ be a finite cover of ![]() $X$ by open subsets such that for every
$X$ by open subsets such that for every ![]() $V\in \mathcal {V}$, the closed subset
$V\in \mathcal {V}$, the closed subset ![]() $V\cap D$ is either empty or is the vanishing locus of an algebraic function
$V\cap D$ is either empty or is the vanishing locus of an algebraic function ![]() $f_V : V\to \mathbb {A}^1$. From Proposition 5.11, the
$f_V : V\to \mathbb {A}^1$. From Proposition 5.11, the ![]() $b$-divisor
$b$-divisor ![]() $\delta \operatorname {Irr}\mathcal {M}$ is effective. Hence,
$\delta \operatorname {Irr}\mathcal {M}$ is effective. Hence,
 \[ \int_{Z} \delta\operatorname{Irr}\mathcal{M} \leq \sum_{V\in \mathcal{V}} \int_{Z\cap V} \delta\operatorname{Irr}\mathcal{M} \leq \sum_{V\in \mathcal{V}} \int_{D\cap V} \delta\operatorname{Irr}\mathcal{M}. \]
\[ \int_{Z} \delta\operatorname{Irr}\mathcal{M} \leq \sum_{V\in \mathcal{V}} \int_{Z\cap V} \delta\operatorname{Irr}\mathcal{M} \leq \sum_{V\in \mathcal{V}} \int_{D\cap V} \delta\operatorname{Irr}\mathcal{M}. \]
Thus, we are left to prove Theorem 6.5 in the case where there exists an open set ![]() $V$ in
$V$ in ![]() $X$ such that
$X$ such that ![]() $Z=D\cap V$ and such that
$Z=D\cap V$ and such that ![]() $Z$ is the vanishing locus of an algebraic function
$Z$ is the vanishing locus of an algebraic function ![]() $f: V\to \mathbb {A}^1$. Observe that the choices of
$f: V\to \mathbb {A}^1$. Observe that the choices of ![]() $V$ and
$V$ and ![]() $f$ depend on
$f$ depend on ![]() $X$ and
$X$ and ![]() $D$ only.
$D$ only.
From Lemma 6.1, we can assume the existence of a proper map ![]() $h : X\to \mathbb {P}^1$ such that
$h : X\to \mathbb {P}^1$ such that ![]() $D$ contains
$D$ contains ![]() $h^{-1}(0)$ and
$h^{-1}(0)$ and ![]() $Z$ is an open subset of
$Z$ is an open subset of ![]() $h^{-1}(0)$. Since
$h^{-1}(0)$. Since ![]() $\delta \operatorname {Irr}\mathcal {M}$ is again effective, we can further assume that
$\delta \operatorname {Irr}\mathcal {M}$ is again effective, we can further assume that ![]() $Z$ is the reduced fibre of
$Z$ is the reduced fibre of ![]() $h$ over
$h$ over ![]() $0$. This case follows from Proposition 6.4. This concludes the proof of Theorem 6.5.
$0$. This case follows from Proposition 6.4. This concludes the proof of Theorem 6.5.
We are now in position to prove cohomological boundedness for surfaces.
Theorem 6.6 Let ![]() $(X,D)$ be a projective normal crossing surface over
$(X,D)$ be a projective normal crossing surface over ![]() $k$. Then, there exists a quadratic polynomial
$k$. Then, there exists a quadratic polynomial ![]() $C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor
$C : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
Proof. From Lemma 2.9, Corollary 2.17 and Remark 2.12, we are left to prove ![]() $\chi$-boundedness for surfaces over
$\chi$-boundedness for surfaces over ![]() $\mathbb {C}$. From Lemma 1.24 and Proposition 2.4, we can suppose that
$\mathbb {C}$. From Lemma 1.24 and Proposition 2.4, we can suppose that ![]() $D$ is a simple normal crossing divisor. We can furthermore suppose that
$D$ is a simple normal crossing divisor. We can furthermore suppose that ![]() $X$ is connected, and thus geometrically connected. From Theorem 5.20, we are left to find a quadratic polynomial
$X$ is connected, and thus geometrically connected. From Theorem 5.20, we are left to find a quadratic polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have we have
$\operatorname {MIC}_r(X,D,R)$, we have we have ![]() $\int _D \delta \operatorname {Irr}\mathcal {M}\leq K(R,r)$. The existence of
$\int _D \delta \operatorname {Irr}\mathcal {M}\leq K(R,r)$. The existence of ![]() $K$ is ensured by Theorem 6.5, which finishes the proof of Theorem 6.6.
$K$ is ensured by Theorem 6.5, which finishes the proof of Theorem 6.6.
6.2 Boundedness and turning locus
To relate the turning locus to de Rham cohomology, we use the following.
Theorem 6.7 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$ where
$k$ where ![]() $D$ is smooth. Let
$D$ is smooth. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then, the following conditions are equivalent:
$\operatorname {MIC}(X,D)$. Then, the following conditions are equivalent:
(i)
 $\mathcal {M}$ has good formal structure along
$\mathcal {M}$ has good formal structure along  $D$;
$D$;(ii) the singular support of
 $\mathcal {M}$ and
$\mathcal {M}$ and  $\operatorname {End}\mathcal {M}$ is contained in
$\operatorname {End}\mathcal {M}$ is contained in  $T^*_X X \cup T^*_D X$.
$T^*_X X \cup T^*_D X$.
If, furthermore, ![]() $k=\mathbb {C}$, the above conditions are equivalent to the following condition.
$k=\mathbb {C}$, the above conditions are equivalent to the following condition.
(iii) The complexes
 $\operatorname {Irr}^*_{D(\mathbb {C})} \mathcal {M}^{\operatorname {an}}$ and
$\operatorname {Irr}^*_{D(\mathbb {C})} \mathcal {M}^{\operatorname {an}}$ and  $\operatorname {Irr}^*_{D(\mathbb {C})} \operatorname {End}\mathcal {M}^{\operatorname {an}}$ are local systems on
$\operatorname {Irr}^*_{D(\mathbb {C})} \operatorname {End}\mathcal {M}^{\operatorname {an}}$ are local systems on  $D(\mathbb {C})$ concentrated in degree
$D(\mathbb {C})$ concentrated in degree  $1$.
$1$.
Proof. From Remark 1.6, we can suppose that ![]() $k=\mathbb {C}$. The fact that condition (i) implies condition (ii) follows from Proposition 5.6. Suppose that condition (ii) holds. From Theorem 1.16, the cohomology sheaves of
$k=\mathbb {C}$. The fact that condition (i) implies condition (ii) follows from Proposition 5.6. Suppose that condition (ii) holds. From Theorem 1.16, the cohomology sheaves of ![]() $\operatorname {Irr}^*_{D(\mathbb {C})} \mathcal {M}$ and
$\operatorname {Irr}^*_{D(\mathbb {C})} \mathcal {M}$ and ![]() $\operatorname {Irr}^*_{D(\mathbb {C})} \operatorname {End}\mathcal {M}$ are local systems on
$\operatorname {Irr}^*_{D(\mathbb {C})} \operatorname {End}\mathcal {M}$ are local systems on ![]() $D(\mathbb {C})$. From Theorem 1.13, the complexes
$D(\mathbb {C})$. From Theorem 1.13, the complexes ![]() $\operatorname {Irr}^*_{D(\mathbb {C})}\mathcal {M}$ and
$\operatorname {Irr}^*_{D(\mathbb {C})}\mathcal {M}$ and ![]() $\operatorname {Irr}^*_{D(\mathbb {C})} \operatorname {End}\mathcal {M}$ are thus necessarily concentrated in degree
$\operatorname {Irr}^*_{D(\mathbb {C})} \operatorname {End}\mathcal {M}$ are thus necessarily concentrated in degree ![]() $1$ and condition (iii) follows. The fact that condition (iii) implies condition (i) is the main result of [Reference TeyssierTey23].
$1$ and condition (iii) follows. The fact that condition (iii) implies condition (i) is the main result of [Reference TeyssierTey23].
Theorem 6.8 Let ![]() $(X,D)$ be a normal crossing surface over an algebraically closed field of characteristic
$(X,D)$ be a normal crossing surface over an algebraically closed field of characteristic ![]() $0$. Let
$0$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $P$ be a point in the smooth locus of
$P$ be a point in the smooth locus of ![]() $D$. Then,
$D$. Then, ![]() $P$ is a turning point of
$P$ is a turning point of ![]() $\mathcal {M}$ if and only if
$\mathcal {M}$ if and only if
In particular,
Proof. From Theorem 6.7, ![]() $P$ is a turning point of
$P$ is a turning point of ![]() $\mathcal {M}$ if and only if
$\mathcal {M}$ if and only if ![]() $T^*_P X$ contributes to
$T^*_P X$ contributes to ![]() $CC(\mathcal {M})+CC(\operatorname {End} \mathcal {M})$. Then, Theorem 6.8 follows from Corollary 5.17.
$CC(\mathcal {M})+CC(\operatorname {End} \mathcal {M})$. Then, Theorem 6.8 follows from Corollary 5.17.
Theorem 6.9 Let ![]() $(X,D)$ be a projective normal crossing pair over
$(X,D)$ be a projective normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $X\to \mathbb {P}$ be a closed embedding in some projective space. Then, there exists a quadratic polynomial
$X\to \mathbb {P}$ be a closed embedding in some projective space. Then, there exists a quadratic polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
Proof. From Proposition 2.4, we can suppose that ![]() $D$ has simple normal crossings. From Remark 1.29, we can suppose that
$D$ has simple normal crossings. From Remark 1.29, we can suppose that ![]() $k$ is algebraically closed. We can thus suppose that
$k$ is algebraically closed. We can thus suppose that ![]() $X$ is geometrically connected. If
$X$ is geometrically connected. If ![]() $X$ is a curve, the turning locus is empty and there is nothing to prove. If
$X$ is a curve, the turning locus is empty and there is nothing to prove. If ![]() $X$ is a surface,
$X$ is a surface, ![]() $\operatorname {TL}(\mathcal {M})$ is a finite set of points. Thus,
$\operatorname {TL}(\mathcal {M})$ is a finite set of points. Thus, ![]() $\deg \operatorname {TL}(\mathcal {M})=|\operatorname {TL}(\mathcal {M})|$. On the other hand, Theorems 6.8 and 6.5 ensure the existence of a quadratic polynomial
$\deg \operatorname {TL}(\mathcal {M})=|\operatorname {TL}(\mathcal {M})|$. On the other hand, Theorems 6.8 and 6.5 ensure the existence of a quadratic polynomial ![]() $L : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor
$L : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ affine in the last variable such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, we have
$\operatorname {MIC}_r(X,D,R)$, we have
Hence, Theorem 6.9 holds in that case. Suppose that ![]() $X$ has dimension
$X$ has dimension ![]() $d\geq 3$. Let
$d\geq 3$. Let ![]() $N$ be the dimension of
$N$ be the dimension of ![]() $\mathbb {P}$. Let
$\mathbb {P}$. Let ![]() $\mathcal {G}$ be the Grassmannian of projective
$\mathcal {G}$ be the Grassmannian of projective ![]() $N-d+2$-spaces in
$N-d+2$-spaces in ![]() $\mathbb {P}$. Let
$\mathbb {P}$. Let ![]() $\eta$ be the generic point of
$\eta$ be the generic point of ![]() $\mathcal {G}$. Let
$\mathcal {G}$. Let ![]() $\mathcal {Q}$ be the universal family of projective
$\mathcal {Q}$ be the universal family of projective ![]() $N-d+2$-spaces in
$N-d+2$-spaces in ![]() $\mathbb {P}$. Then, there is the following commutative diagram with cartesian squares.
$\mathbb {P}$. Then, there is the following commutative diagram with cartesian squares.

Let ![]() $\eta$ as a subscript indicate a pull-back along
$\eta$ as a subscript indicate a pull-back along ![]() $X_{\eta }\to X$. Let
$X_{\eta }\to X$. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $r\geq 0$ be an integer. Let
$r\geq 0$ be an integer. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}_r(X,D,R)$. From Kedlaya's purity Theorem 1.31, the closed set
$\operatorname {MIC}_r(X,D,R)$. From Kedlaya's purity Theorem 1.31, the closed set ![]() $\operatorname {TL}(\mathcal {M})$ has pure dimension
$\operatorname {TL}(\mathcal {M})$ has pure dimension ![]() $d-2$. Hence,
$d-2$. Hence, ![]() $\deg \operatorname {TL}(\mathcal {M})$ is the cardinal of
$\deg \operatorname {TL}(\mathcal {M})$ is the cardinal of ![]() $\operatorname {TL}(\mathcal {M})\cap H$ where
$\operatorname {TL}(\mathcal {M})\cap H$ where ![]() $H$ is a generic projective
$H$ is a generic projective ![]() $N-d+2$-spaces of
$N-d+2$-spaces of ![]() $\mathbb {P}$. Thus,
$\mathbb {P}$. Thus,
where the last equality follows by Remark 1.29. Since ![]() $\mathcal {M}_\eta$ lies in
$\mathcal {M}_\eta$ lies in ![]() $\operatorname {MIC}_r(X_\eta,D_\eta,R_\eta )$ with
$\operatorname {MIC}_r(X_\eta,D_\eta,R_\eta )$ with ![]() $(X_\eta,D_\eta )$ a normal crossing surface over
$(X_\eta,D_\eta )$ a normal crossing surface over ![]() $\eta$, Theorem 6.9 follows from the surface case.
$\eta$, Theorem 6.9 follows from the surface case.
As an application of the above theorem, we deduce the following.
Theorem 6.10 Let ![]() $(X,D)$ be a projective normal crossing pair over
$(X,D)$ be a projective normal crossing pair over ![]() $k$. Then, there exists a quadratic polynomial
$k$. Then, there exists a quadratic polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_r(X,D,R)$, the number of irreducible components of
$\operatorname {MIC}_r(X,D,R)$, the number of irreducible components of ![]() $\operatorname {TL}(\mathcal {M})$ is smaller than
$\operatorname {TL}(\mathcal {M})$ is smaller than ![]() $K(R,r)$.
$K(R,r)$.
Proof. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $r\geq 0$ be an integer. Let
$r\geq 0$ be an integer. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}_r(X,D,R)$. Let
$\operatorname {MIC}_r(X,D,R)$. Let ![]() $Z_1,\ldots, Z_n$ be the irreducible components of
$Z_1,\ldots, Z_n$ be the irreducible components of ![]() $\operatorname {TL}(\mathcal {M})$. From Kedlaya's purity Theorem 1.31, the
$\operatorname {TL}(\mathcal {M})$. From Kedlaya's purity Theorem 1.31, the ![]() $Z_i$ have the same dimension
$Z_i$ have the same dimension ![]() $\dim X-2$. Hence,
$\dim X-2$. Hence, ![]() $\deg \operatorname {TL}(\mathcal {M})=\deg Z_1+\cdots +\deg Z_n$. Since each
$\deg \operatorname {TL}(\mathcal {M})=\deg Z_1+\cdots +\deg Z_n$. Since each ![]() $\deg Z_i$ is strictly positive, we deduce
$\deg Z_i$ is strictly positive, we deduce ![]() $n\leq \deg \operatorname {TL}(\mathcal {M})$. Thus, Theorem 6.10 follows from Theorem 6.9.
$n\leq \deg \operatorname {TL}(\mathcal {M})$. Thus, Theorem 6.10 follows from Theorem 6.9.
7. Lefschetz recognition principle
Lemma 7.1 Let ![]() $\mathbb {P}$ be a projective space over
$\mathbb {P}$ be a projective space over ![]() $k$. Let
$k$. Let ![]() $X\subset \mathbb {P}$ be a smooth subvariety of pure dimension
$X\subset \mathbb {P}$ be a smooth subvariety of pure dimension ![]() $n\geq 2$. Let
$n\geq 2$. Let ![]() $C',C''\subset T^\ast X$ be closed conical subsets of pure dimension
$C',C''\subset T^\ast X$ be closed conical subsets of pure dimension ![]() $n$ where the base of
$n$ where the base of ![]() $C''$ has dimension at most
$C''$ has dimension at most ![]() $n-2$. Put
$n-2$. Put ![]() $C=C'\cup C''$. Let
$C=C'\cup C''$. Let ![]() $S\subset X$ be a closed subset of dimension
$S\subset X$ be a closed subset of dimension ![]() $\leq n-2$ containing the base of
$\leq n-2$ containing the base of ![]() $C''$. Let
$C''$. Let ![]() $Y\subset \mathbb {P}$ be a smooth hypersurface transverse to
$Y\subset \mathbb {P}$ be a smooth hypersurface transverse to ![]() $X$ such that
$X$ such that ![]() $X\cap Y \to X$ is
$X\cap Y \to X$ is ![]() $C'$-transversal and
$C'$-transversal and ![]() $X\cap Y \cap S$ has dimension
$X\cap Y \cap S$ has dimension ![]() $< n-2$. Then, for every sufficiently generic hyperplanes
$< n-2$. Then, for every sufficiently generic hyperplanes ![]() $E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$, the following hold.
$E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$, the following hold.
(i) The commutative diagram
is a diagram of smooth varieties such that for every
 $j=1,\ldots, n-2$, the map
is
$j=1,\ldots, n-2$, the map
is \[ X\cap E_1\cap \cdots \cap E_{j} \to X\cap E_1\cap \cdots \cap E_{j-1} \]
\[ X\cap E_1\cap \cdots \cap E_{j} \to X\cap E_1\cap \cdots \cap E_{j-1} \]
 $i_{j-1}^{\circ }(C)$-transversal.
$i_{j-1}^{\circ }(C)$-transversal.(ii) The scheme
 $T:=X\cap Y\cap E_1\cap \cdots \cap E_{n-2}$ is a smooth curve of
$T:=X\cap Y\cap E_1\cap \cdots \cap E_{n-2}$ is a smooth curve of  $X$ avoiding
$X$ avoiding  $S$ such that
$S$ such that  $T\to X$ is
$T\to X$ is  $C$-transversal.
$C$-transversal.(iii) The map
 $T\to X\cap E_1\cap \cdots \cap E_{n-2}$ is
$T\to X\cap E_1\cap \cdots \cap E_{n-2}$ is  $i_{n-2}^{\circ }(C)$-transversal.
$i_{n-2}^{\circ }(C)$-transversal.
Proof. Claim (i) follows from an iterative use of Lemmas 1.5 and 1.4(iii). Let us prove claim (ii). The scheme ![]() $X\cap Y$ is a smooth variety of dimension
$X\cap Y$ is a smooth variety of dimension ![]() $n-1$ and
$n-1$ and ![]() $X\cap Y \cap S\subset X\cap Y$ is a closed subset of dimension
$X\cap Y \cap S\subset X\cap Y$ is a closed subset of dimension ![]() $< n-2$. For
$< n-2$. For ![]() $E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, Bertini's theorem ensures that
$E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, Bertini's theorem ensures that ![]() $T:=X\cap Y\cap E_1\cap \cdots \cap E_{n-2} \subset X\cap Y$ is a smooth curve avoiding
$T:=X\cap Y\cap E_1\cap \cdots \cap E_{n-2} \subset X\cap Y$ is a smooth curve avoiding ![]() $S$. An iterative use of Lemmas 1.5 and 1.4(iii) applied to
$S$. An iterative use of Lemmas 1.5 and 1.4(iii) applied to
ensures that for ![]() $E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the map
$E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the map ![]() $T\to X$ is
$T\to X$ is ![]() $C'$-transversal. Since
$C'$-transversal. Since ![]() $T$ avoid
$T$ avoid ![]() $S$ and since
$S$ and since ![]() $S$ contains the base of
$S$ contains the base of ![]() $C''$, the map
$C''$, the map ![]() $T\to X$ is also
$T\to X$ is also ![]() $C''$-transversal. From Lemma 1.4(ii), we deduce that
$C''$-transversal. From Lemma 1.4(ii), we deduce that ![]() $T\to X$ is
$T\to X$ is ![]() $C$-transversal. Claim (ii) is thus proved. Claim (iii) follows from Lemma 1.4(iii) applied to the following.
$C$-transversal. Claim (ii) is thus proved. Claim (iii) follows from Lemma 1.4(iii) applied to the following.
Proposition 7.2 Let ![]() $(X,D)$ be a projective simple normal crossing pair of dimension
$(X,D)$ be a projective simple normal crossing pair of dimension ![]() $n\geq 2$ over
$n\geq 2$ over ![]() $k$. Let
$k$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Let
$X\to \mathbb {P}$ be a closed immersion in some projective space. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $H$ be a hyperplane such that:
$H$ be a hyperplane such that:
(i)
 $H$ is transverse to
$H$ is transverse to  $X$ and
$X$ and  $X\cap H\to X$ is
$X\cap H\to X$ is  $SS(\mathcal {O}_X(\ast D))$-transversal;
$SS(\mathcal {O}_X(\ast D))$-transversal;(ii)
 $X\cap H$ does not contain any irreducible component of
$X\cap H$ does not contain any irreducible component of  $\operatorname {TL}(\mathcal {M})$.
$\operatorname {TL}(\mathcal {M})$.
Then, for every ![]() $E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the restriction morphism
$E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the restriction morphism
is an isomorphism, where ![]() $T=X\cap H \cap E_1 \cap \cdots \cap E_{n-2}$.
$T=X\cap H \cap E_1 \cap \cdots \cap E_{n-2}$.
Proof. Let ![]() $C''$ be the union of irreducible components of
$C''$ be the union of irreducible components of ![]() $SS(\mathcal {M})$ whose bases are subsets of
$SS(\mathcal {M})$ whose bases are subsets of ![]() $\operatorname {TL}(\mathcal {M})$. Then, Proposition 5.6 yields
$\operatorname {TL}(\mathcal {M})$. Then, Proposition 5.6 yields
Since ![]() $\dim \operatorname {TL}(\mathcal {M})=n-2$, the conditions from Lemma 7.1 are satisfied for
$\dim \operatorname {TL}(\mathcal {M})=n-2$, the conditions from Lemma 7.1 are satisfied for ![]() $Y=H$,
$Y=H$, ![]() $C'=SS(\mathcal {O}_X(\ast D))$ and
$C'=SS(\mathcal {O}_X(\ast D))$ and ![]() $C''$, and
$C''$, and ![]() $S=\operatorname {TL}(\mathcal {M})$. Thus, for every
$S=\operatorname {TL}(\mathcal {M})$. Thus, for every ![]() $E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the commutative diagram
$E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the commutative diagram

is a diagram of smooth varieties such that for every ![]() $j=1,\ldots, n-2$, the map
$j=1,\ldots, n-2$, the map
is ![]() $i_{j-1}^{\circ }(SS(\mathcal {M}))$-transversal and
$i_{j-1}^{\circ }(SS(\mathcal {M}))$-transversal and ![]() $T\to X\cap E_1\cap \cdots \cap E_{n-2}$ is
$T\to X\cap E_1\cap \cdots \cap E_{n-2}$ is ![]() $i_{n-2}^{\circ }(SS(\mathcal {M}))$-transversal. From Theorem 1.20, the horizontal and vertical arrows of the above diagram are thus non-characteristic for the successive restrictions of
$i_{n-2}^{\circ }(SS(\mathcal {M}))$-transversal. From Theorem 1.20, the horizontal and vertical arrows of the above diagram are thus non-characteristic for the successive restrictions of ![]() $\mathcal {M}$. From Proposition 2.13, we deduce that each arrow of the diagram
$\mathcal {M}$. From Proposition 2.13, we deduce that each arrow of the diagram
induced by the successive restrictions of ![]() $\mathcal {M}$ are isomorphisms. This concludes the proof of Proposition 7.2.
$\mathcal {M}$ are isomorphisms. This concludes the proof of Proposition 7.2.
Corollary 7.4 Let ![]() $(X,D)$ be a projective simple normal crossing pair of dimension
$(X,D)$ be a projective simple normal crossing pair of dimension ![]() $n\geq 2$ over
$n\geq 2$ over ![]() $k$. Let
$k$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Let
$X\to \mathbb {P}$ be a closed immersion in some projective space. Let ![]() $\mathcal {M}_1,\mathcal {M}_2$ be objects of
$\mathcal {M}_1,\mathcal {M}_2$ be objects of ![]() $\operatorname {MIC}(X,D)$. Let
$\operatorname {MIC}(X,D)$. Let ![]() $H$ be a hyperplane such that:
$H$ be a hyperplane such that:
(i)
 $H$ is transverse to
$H$ is transverse to  $X$ and
$X$ and  $X\cap H\to X$ is
$X\cap H\to X$ is  $SS(\mathcal {O}_X(\ast D))$-transversal;
$SS(\mathcal {O}_X(\ast D))$-transversal;(ii)
 $X\cap H$ does not contain any irreducible component of
$X\cap H$ does not contain any irreducible component of  $\operatorname {TL}({\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1,\mathcal {M}_2))$.
$\operatorname {TL}({\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1,\mathcal {M}_2))$.
Then, for every ![]() $E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the restriction morphism
$E_1,\ldots, E_{n-2} \in \mathbb {P}^{\vee }$ sufficiently generic, the restriction morphism
is an isomorphism, where ![]() $T=X\cap H \cap E_1 \cap \cdots \cap E_{n-2}$.
$T=X\cap H \cap E_1 \cap \cdots \cap E_{n-2}$.
Theorem 7.5 Let ![]() $(X,D)$ be a projective simple normal crossing pair of dimension
$(X,D)$ be a projective simple normal crossing pair of dimension ![]() $n\geq 2$ over
$n\geq 2$ over ![]() $k$. Let
$k$. Let ![]() $X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a polynomial
$X\to \mathbb {P}$ be a closed immersion in some projective space. Then, there exists a polynomial ![]() $K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree
$K : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ of degree ![]() $4$ such that for every effective divisor
$4$ such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$, every set
$r\geq 0$, every set ![]() $\mathcal {H}$ of
$\mathcal {H}$ of ![]() $K(R,r)$ hyperplanes satisfying the following conditions:
$K(R,r)$ hyperplanes satisfying the following conditions:
(i)
 $H$ is transverse to
$H$ is transverse to  $X$ and
$X$ and  $X\cap H\to X$ is
$X\cap H\to X$ is  $SS(\mathcal {O}_X(\ast D))$-transversal for every
$SS(\mathcal {O}_X(\ast D))$-transversal for every  $H\in \mathcal {H}$;
$H\in \mathcal {H}$;(ii)
 $D\cap H, H\in \mathcal {H}$ are closed subsets of
$D\cap H, H\in \mathcal {H}$ are closed subsets of  $D$ of pure dimension
$D$ of pure dimension  $n-2$ with two by two distinct irreducible components;
$n-2$ with two by two distinct irreducible components;
realizes the Lefschetz recognition principle for ![]() $\operatorname {MIC}_r(X,D,R)$ (Definition 0.2). In particular, there is a dense open subset of
$\operatorname {MIC}_r(X,D,R)$ (Definition 0.2). In particular, there is a dense open subset of ![]() $K(R,r)$-uples of hyperplanes realizing the Lefschetz recognition principle for
$K(R,r)$-uples of hyperplanes realizing the Lefschetz recognition principle for ![]() $\operatorname {MIC}_r(X,D,R)$.
$\operatorname {MIC}_r(X,D,R)$.
Proof. From Theorem 6.10, there exists a quadratic polynomial ![]() $L : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor
$L : \operatorname {Div}(X,D)\oplus \mathbb {Z}\to \mathbb {Z}$ such that for every effective divisor ![]() $R$ of
$R$ of ![]() $X$ supported on
$X$ supported on ![]() $D$, for every integer
$D$, for every integer ![]() $r\geq 0$ and every object
$r\geq 0$ and every object ![]() $\mathcal {M}$ of
$\mathcal {M}$ of ![]() $\operatorname {MIC}_{4r^2}(X,D,2r^2 \cdot R)$, the number of irreducible components of
$\operatorname {MIC}_{4r^2}(X,D,2r^2 \cdot R)$, the number of irreducible components of ![]() $\operatorname {TL}(\mathcal {M})\subset D$ is smaller than
$\operatorname {TL}(\mathcal {M})\subset D$ is smaller than ![]() $L(2r^2 \cdot R,4r^2)$. Put
$L(2r^2 \cdot R,4r^2)$. Put
Choose a set ![]() $\mathcal {H}$ of
$\mathcal {H}$ of ![]() $K(R,r)$ hyperplanes satisfying conditions (i) and (ii) above. We want to show that
$K(R,r)$ hyperplanes satisfying conditions (i) and (ii) above. We want to show that ![]() $\mathcal {H}$ realizes the Lefschetz recognition principle for
$\mathcal {H}$ realizes the Lefschetz recognition principle for ![]() $\operatorname {MIC}_r(X,D,R)$. Let
$\operatorname {MIC}_r(X,D,R)$. Let ![]() $\mathcal {M}_1,\mathcal {M}_2 \in \operatorname {MIC}_r(X,D,R)$ such that
$\mathcal {M}_1,\mathcal {M}_2 \in \operatorname {MIC}_r(X,D,R)$ such that ![]() $\mathcal {M}_1|_{X\cap H}$ and
$\mathcal {M}_1|_{X\cap H}$ and ![]() $\mathcal {M}_2|_{X\cap H}$ are isomorphic for
$\mathcal {M}_2|_{X\cap H}$ are isomorphic for ![]() $H\in \mathcal {H}$. In particular, for every
$H\in \mathcal {H}$. In particular, for every ![]() $H\in \mathcal {H}$ and every smooth subvariety
$H\in \mathcal {H}$ and every smooth subvariety ![]() $T\subset X\cap H$, the connections
$T\subset X\cap H$, the connections ![]() $\mathcal {M}_1|_T$ and
$\mathcal {M}_1|_T$ and ![]() $\mathcal {M}_2|_T$ are isomorphic. We now want to show that
$\mathcal {M}_2|_T$ are isomorphic. We now want to show that ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ are isomorphic. To do this, it is enough to show the existence of
$\mathcal {M}_2$ are isomorphic. To do this, it is enough to show the existence of ![]() $H\in \mathcal {H}$ and a smooth subvariety
$H\in \mathcal {H}$ and a smooth subvariety ![]() $T\subset X\cap H$ such that
$T\subset X\cap H$ such that
is an isomorphism for every ![]() $a,b\in \{1,2\}$. From Corollary 7.4, it is enough to show the existence of
$a,b\in \{1,2\}$. From Corollary 7.4, it is enough to show the existence of ![]() $H\in \mathcal {H}$ such that
$H\in \mathcal {H}$ such that ![]() $X\cap H$ does not contain any irreducible component of
$X\cap H$ does not contain any irreducible component of ![]() $\operatorname {TL}({\mathcal {H}}\! \operatorname {om}(\mathcal {M}_a,\mathcal {M}_b)), a,b\in \{1,2\}$. If we put
$\operatorname {TL}({\mathcal {H}}\! \operatorname {om}(\mathcal {M}_a,\mathcal {M}_b)), a,b\in \{1,2\}$. If we put
we have
Since turning loci have pure dimension ![]() $n-2$ in virtue of Theorem 1.31, we deduce that the irreducible components of the
$n-2$ in virtue of Theorem 1.31, we deduce that the irreducible components of the ![]() $\operatorname {TL}({\mathcal {H}}\! \operatorname {om}(\mathcal {M}_a,\mathcal {M}_b))$,
$\operatorname {TL}({\mathcal {H}}\! \operatorname {om}(\mathcal {M}_a,\mathcal {M}_b))$, ![]() $a,b\in \{1,2\}$ are irreducible components of
$a,b\in \{1,2\}$ are irreducible components of ![]() $\operatorname {TL}(\mathcal {M})$. Thus, it is enough to show the existence of
$\operatorname {TL}(\mathcal {M})$. Thus, it is enough to show the existence of ![]() $H\in \mathcal {H}$ such that
$H\in \mathcal {H}$ such that ![]() $X\cap H$ does not contain any irreducible component of
$X\cap H$ does not contain any irreducible component of ![]() $\operatorname {TL}(\mathcal {M})$. Note from Proposition 2.2 that
$\operatorname {TL}(\mathcal {M})$. Note from Proposition 2.2 that ![]() $\mathcal {M}$ is an object of
$\mathcal {M}$ is an object of ![]() $\operatorname {MIC}_{4r^2}(X,D,2r^2 \cdot R)$. Hence,
$\operatorname {MIC}_{4r^2}(X,D,2r^2 \cdot R)$. Hence, ![]() $\operatorname {TL}(\mathcal {M})$ has strictly less than
$\operatorname {TL}(\mathcal {M})$ has strictly less than ![]() $K(R,r)$ irreducible components. Thus, condition (ii) above ensures the existence of the sought-after hyperplane.
$K(R,r)$ irreducible components. Thus, condition (ii) above ensures the existence of the sought-after hyperplane.
8. Tannakian Lefschetz theorem
As usual, ![]() $k$ denotes a field of characteristic
$k$ denotes a field of characteristic ![]() $0$. For an abelian category
$0$. For an abelian category ![]() $\mathcal {C}$, we denote by
$\mathcal {C}$, we denote by ![]() $\mathcal {C}^{\operatorname {ss}}$ the full subcategory of
$\mathcal {C}^{\operatorname {ss}}$ the full subcategory of ![]() $\mathcal {C}$ spanned by the semisimple objects. If
$\mathcal {C}$ spanned by the semisimple objects. If ![]() $F : \mathcal {C}\to \mathcal {D}$ is an additive functor between abelian categories, we let
$F : \mathcal {C}\to \mathcal {D}$ is an additive functor between abelian categories, we let ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ be the full subcategory of
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ be the full subcategory of ![]() $\mathcal {C}$ spanned by the objects sent in
$\mathcal {C}$ spanned by the objects sent in ![]() $\mathcal {D}^{\operatorname {ss}}$ by
$\mathcal {D}^{\operatorname {ss}}$ by ![]() $F$.
$F$.
As a general reference for Tannakian categories, let us mention [Reference Deligne and MilneDM82]. If ![]() $(\mathcal {C},\otimes _\mathcal {C})$ is a Tannakian category and if
$(\mathcal {C},\otimes _\mathcal {C})$ is a Tannakian category and if ![]() $M$ is an object of
$M$ is an object of ![]() $\mathcal {C}$, we denote by
$\mathcal {C}$, we denote by ![]() $\langle M\rangle$ the Tannakian subcategory of
$\langle M\rangle$ the Tannakian subcategory of ![]() $\mathcal {C}$ generated by
$\mathcal {C}$ generated by ![]() $M$. If
$M$. If ![]() $\omega : \mathcal {C} \to \operatorname {Vect}_k$ is a neutralization for
$\omega : \mathcal {C} \to \operatorname {Vect}_k$ is a neutralization for ![]() $(\mathcal {C},\otimes _\mathcal {C})$, we denote by
$(\mathcal {C},\otimes _\mathcal {C})$, we denote by ![]() $\pi _1( M,\omega )$ the Tannakian algebraic group of
$\pi _1( M,\omega )$ the Tannakian algebraic group of ![]() $\langle M\rangle$ at
$\langle M\rangle$ at ![]() $\omega$.
$\omega$.
Example 8.1 Let ![]() $(X,D)$ be a pair over
$(X,D)$ be a pair over ![]() $k$. Then
$k$. Then ![]() $(\operatorname {MIC}(X,D),\otimes _{\mathcal {O}_X(\ast D)})$ is an abelian rigid tensor category over
$(\operatorname {MIC}(X,D),\otimes _{\mathcal {O}_X(\ast D)})$ is an abelian rigid tensor category over ![]() $k$. For a morphism of pairs
$k$. For a morphism of pairs ![]() $f : (Y,E)\to (X,D)$ over
$f : (Y,E)\to (X,D)$ over ![]() $k$, the pull-back
$k$, the pull-back ![]() $f^+ : \operatorname {MIC}(X,D)\to \operatorname {MIC}(Y,E)$ is an exact tensor functor. If, furthermore,
$f^+ : \operatorname {MIC}(X,D)\to \operatorname {MIC}(Y,E)$ is an exact tensor functor. If, furthermore, ![]() $X$ is connected and
$X$ is connected and ![]() $k$ is algebraically closed, the restriction to any closed point of
$k$ is algebraically closed, the restriction to any closed point of ![]() $X\setminus D$ endows
$X\setminus D$ endows ![]() $(\operatorname {MIC}(X,D),\otimes _{\mathcal {O}_X(\ast D)})$ with a structure of neutral Tannakian category.
$(\operatorname {MIC}(X,D),\otimes _{\mathcal {O}_X(\ast D)})$ with a structure of neutral Tannakian category.
Lemma 8.2 Let ![]() $F: (\mathcal {C},\otimes _\mathcal {C}) \to (\mathcal {D},\otimes _\mathcal {D})$ be an exact tensor functor between neutral Tannakian categories over
$F: (\mathcal {C},\otimes _\mathcal {C}) \to (\mathcal {D},\otimes _\mathcal {D})$ be an exact tensor functor between neutral Tannakian categories over ![]() $k$. Then,
$k$. Then, ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is a neutral Tannakian subcategory of
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is a neutral Tannakian subcategory of ![]() $(\mathcal {C},\otimes _\mathcal {C})$.
$(\mathcal {C},\otimes _\mathcal {C})$.
Proof. Let ![]() $f : X\rightarrow Y$ be a morphism in
$f : X\rightarrow Y$ be a morphism in ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ and let
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ and let ![]() $K$ be its kernel in
$K$ be its kernel in ![]() $\mathcal {C}$. Since
$\mathcal {C}$. Since ![]() $F$ is exact,
$F$ is exact, ![]() $F(K)\simeq \operatorname {Ker} F(f)$ is semisimple since
$F(K)\simeq \operatorname {Ker} F(f)$ is semisimple since ![]() $F(X)$ is semisimple [Reference MilneMil17, 4.14]. Hence,
$F(X)$ is semisimple [Reference MilneMil17, 4.14]. Hence, ![]() $K$ lies in
$K$ lies in ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ and similarly for the cokernel of
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ and similarly for the cokernel of ![]() $f$. Thus,
$f$. Thus, ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is an abelian subcategory of
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is an abelian subcategory of ![]() $\mathcal {C}$. Let
$\mathcal {C}$. Let ![]() $X,Y$ be objects of
$X,Y$ be objects of ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$. Since
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$. Since ![]() $F$ is a tensor functor between rigid tensor categories, we have
$F$ is a tensor functor between rigid tensor categories, we have
where the first equivalence follows from [Reference Deligne and MilneDM82, 1.9] and the second from [Reference Deligne and MilneDM82, 1.7]. Since the tensor product of two semisimple finite-dimensional representations of a group is again semisimple [Reference ChevalleyChe54, p.88], we know that ![]() $F(X)^{\vee }\otimes _{\mathcal {D}} F(Y)$ is semisimple. Hence,
$F(X)^{\vee }\otimes _{\mathcal {D}} F(Y)$ is semisimple. Hence, ![]() $\underline {\mathrm {Hom}}(X,Y)$ lies in
$\underline {\mathrm {Hom}}(X,Y)$ lies in ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$. Furthermore, the identity object of
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$. Furthermore, the identity object of ![]() $\mathcal {C}$ lies in
$\mathcal {C}$ lies in ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$. Hence,
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$. Hence, ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is stable under finite tensor product and dual. Thus,
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is stable under finite tensor product and dual. Thus, ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is a rigid abelian tensor subcategory of
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ is a rigid abelian tensor subcategory of ![]() $(\mathcal {C},\otimes _\mathcal {C})$. A neutralization of
$(\mathcal {C},\otimes _\mathcal {C})$. A neutralization of ![]() $(\mathcal {C},\otimes _\mathcal {C})$ induces a neutralization of
$(\mathcal {C},\otimes _\mathcal {C})$ induces a neutralization of ![]() $F^{-1}(\mathcal {D}^{\operatorname {ss}})$ and the proof of Lemma 8.2 is complete.
$F^{-1}(\mathcal {D}^{\operatorname {ss}})$ and the proof of Lemma 8.2 is complete.
Remark 8.3 Lemma 8.2 applied to the identity functor implies that ![]() $\mathcal {C}^{\operatorname {ss}}$ is a neutral Tannakian subcategory of
$\mathcal {C}^{\operatorname {ss}}$ is a neutral Tannakian subcategory of ![]() $(\mathcal {C},\otimes _\mathcal {C})$.
$(\mathcal {C},\otimes _\mathcal {C})$.
The following ground-breaking theorem is due to Mochizuki [Reference MochizukiMoc11, § 13.2.3].
Theorem 8.4 Let ![]() $(X,D)$ be a projective simple normal crossing pair over
$(X,D)$ be a projective simple normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $\mathcal {L}$ be an ample line bundle on
$\mathcal {L}$ be an ample line bundle on ![]() $X$. Let
$X$. Let ![]() $\mathcal {M}$ be a semisimple object of
$\mathcal {M}$ be a semisimple object of ![]() $\operatorname {MIC}(X,D)$. Then, for every
$\operatorname {MIC}(X,D)$. Then, for every ![]() $m_1>0$, there is
$m_1>0$, there is ![]() $m>m_1$ such that for every generic hyperplane
$m>m_1$ such that for every generic hyperplane ![]() $H$ of
$H$ of ![]() $\mathcal {L}^m$, the restriction
$\mathcal {L}^m$, the restriction ![]() $\mathcal {M}|_{X\cap H}$ is a semisimple object of
$\mathcal {M}|_{X\cap H}$ is a semisimple object of ![]() $\operatorname {MIC}(X\cap H,D\cap H)$.
$\operatorname {MIC}(X\cap H,D\cap H)$.
Remark 8.5 In the statement of Theorem 8.4, the integer ![]() $m$ depends on
$m$ depends on ![]() $\mathcal {M}$.
$\mathcal {M}$.
Corollary 8.6 Let ![]() $(X,D)$ be a connected projective simple normal crossing pair over
$(X,D)$ be a connected projective simple normal crossing pair over ![]() $k$. Assume that
$k$. Assume that ![]() $k$ is algebraically closed. Let
$k$ is algebraically closed. Let ![]() $\mathcal {L}$ be an ample line bundle on
$\mathcal {L}$ be an ample line bundle on ![]() $X$. Let
$X$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then, for every integer
$\operatorname {MIC}(X,D)$. Then, for every integer ![]() $m_1>0$, there is an integer
$m_1>0$, there is an integer ![]() $m>m_1$ such that for every generic hyperplane
$m>m_1$ such that for every generic hyperplane ![]() $H$ of
$H$ of ![]() $\mathcal {L}^m$, for every semisimple object
$\mathcal {L}^m$, for every semisimple object ![]() $\mathcal {N}$ of
$\mathcal {N}$ of ![]() $\langle \mathcal {M}\rangle$, the restriction
$\langle \mathcal {M}\rangle$, the restriction ![]() $\mathcal {N}|_{X\cap H}$ is a semisimple object of
$\mathcal {N}|_{X\cap H}$ is a semisimple object of ![]() $\operatorname {MIC}(X\cap H,D\cap H)$.
$\operatorname {MIC}(X\cap H,D\cap H)$.
Proof. Since ![]() $\langle \mathcal {M}\rangle$ admits a tensor generator, the general yoga of neutral Tannakian categories [Reference Deligne and MilneDM82, 2.20 (b)] ensures that so does
$\langle \mathcal {M}\rangle$ admits a tensor generator, the general yoga of neutral Tannakian categories [Reference Deligne and MilneDM82, 2.20 (b)] ensures that so does ![]() $\langle \mathcal {M}\rangle ^{\operatorname {ss}}$. Let
$\langle \mathcal {M}\rangle ^{\operatorname {ss}}$. Let ![]() $\mathcal {N}$ be a tensor generator for
$\mathcal {N}$ be a tensor generator for ![]() $\langle \mathcal {M}\rangle ^{\operatorname {ss}}$. From Mochizuki's Theorem 8.4 applied to
$\langle \mathcal {M}\rangle ^{\operatorname {ss}}$. From Mochizuki's Theorem 8.4 applied to ![]() $\mathcal {N}$, there exists an integer
$\mathcal {N}$, there exists an integer ![]() $m>m_1$ such that the set of hyperplanes
$m>m_1$ such that the set of hyperplanes ![]() $H$ of
$H$ of ![]() $\mathcal {L}^m$ with
$\mathcal {L}^m$ with ![]() $\mathcal {N}|_{X\cap H}$ semisimple contains a dense open subset
$\mathcal {N}|_{X\cap H}$ semisimple contains a dense open subset ![]() $V$ of
$V$ of ![]() $\mathbb {P}(\Gamma (X,\mathcal {L}^m))^{\vee }$. Let
$\mathbb {P}(\Gamma (X,\mathcal {L}^m))^{\vee }$. Let ![]() $H\in V(k)$. Let
$H\in V(k)$. Let ![]() $F :\langle \mathcal {M}\rangle \to \operatorname {MIC}(X\cap H, D\cap H)$ be the exact tensor functor given by the restriction to
$F :\langle \mathcal {M}\rangle \to \operatorname {MIC}(X\cap H, D\cap H)$ be the exact tensor functor given by the restriction to ![]() $X\cap H$. Then, Lemma 8.2 ensures that
$X\cap H$. Then, Lemma 8.2 ensures that ![]() $F^{-1}(\operatorname {MIC}(X\cap H, D\cap H)^{\operatorname {ss}})$ is a neutral Tannakian subcategory of
$F^{-1}(\operatorname {MIC}(X\cap H, D\cap H)^{\operatorname {ss}})$ is a neutral Tannakian subcategory of ![]() $\langle \mathcal {M}\rangle$. Since it contains
$\langle \mathcal {M}\rangle$. Since it contains ![]() $\mathcal {N}$, it also contains
$\mathcal {N}$, it also contains ![]() $\langle \mathcal {M}\rangle ^{\operatorname {ss}}$. The proof of Corollary 8.6 is thus complete.
$\langle \mathcal {M}\rangle ^{\operatorname {ss}}$. The proof of Corollary 8.6 is thus complete.
Lemma 8.7 Let ![]() $(X,D)$ be a projective pair of dimension at least
$(X,D)$ be a projective pair of dimension at least ![]() $2$ over
$2$ over ![]() $k$. Assume that
$k$. Assume that ![]() $k$ is uncountable. Let
$k$ is uncountable. Let ![]() $\mathcal {L}$ be a very ample line bundle on
$\mathcal {L}$ be a very ample line bundle on ![]() $X$. Let
$X$. Let ![]() $\mathcal {C}$ be a full subcategory of
$\mathcal {C}$ be a full subcategory of ![]() $\operatorname {MIC}(X,D)$ spanned by a countable number of objects. Then, for every very generic hyperplane
$\operatorname {MIC}(X,D)$ spanned by a countable number of objects. Then, for every very generic hyperplane ![]() $H$ of
$H$ of ![]() $\mathcal {L}$, the restriction to
$\mathcal {L}$, the restriction to ![]() $X\cap H$ induces a fully faithful functor on
$X\cap H$ induces a fully faithful functor on ![]() $\mathcal {C}$.
$\mathcal {C}$.
Proof. Let ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ be objects in
$\mathcal {M}_2$ be objects in ![]() $\mathcal {C}$. From Lemma 1.5, the set of hyperplanes
$\mathcal {C}$. From Lemma 1.5, the set of hyperplanes ![]() $H$ of
$H$ of ![]() $\mathcal {L}$ transverse to
$\mathcal {L}$ transverse to ![]() $X$ such that
$X$ such that ![]() $X\cap H\to X$ is non-characteristic for
$X\cap H\to X$ is non-characteristic for ![]() ${\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1, \mathcal {M}_2)$ contains a dense open subset
${\mathcal {H}}\! \operatorname {om}(\mathcal {M}_1, \mathcal {M}_2)$ contains a dense open subset ![]() $V(\mathcal {M}_1,\mathcal {M}_2)$. From Corollary 7.4, the set of hyperplanes
$V(\mathcal {M}_1,\mathcal {M}_2)$. From Corollary 7.4, the set of hyperplanes ![]() $H$ of
$H$ of ![]() $\mathcal {L}$ transverse to
$\mathcal {L}$ transverse to ![]() $X$ such that
$X$ such that
is an isomorphism contains ![]() $V(\mathcal {M}_1,\mathcal {M}_2)$. Then the intersection of the
$V(\mathcal {M}_1,\mathcal {M}_2)$. Then the intersection of the ![]() $V(\mathcal {M}_1,\mathcal {M}_2)$ for
$V(\mathcal {M}_1,\mathcal {M}_2)$ for ![]() $\mathcal {M}_1, \mathcal {M}_2 \in \mathcal {C}$ gives the sought-after set of very generic hyperplanes.
$\mathcal {M}_1, \mathcal {M}_2 \in \mathcal {C}$ gives the sought-after set of very generic hyperplanes.
Before proving Theorem 8.10, we recall the following abstract lemma [Reference StalderSta08, 1.1.4].
Lemma 8.8 Let ![]() $F : \mathcal {C}\to \mathcal {D}$ be an exact
$F : \mathcal {C}\to \mathcal {D}$ be an exact ![]() $k$-linear fully faithful functor between abelian categories over
$k$-linear fully faithful functor between abelian categories over ![]() $k$. Assume that for every object
$k$. Assume that for every object ![]() $M$ of
$M$ of ![]() $\mathcal {C}$, the length of
$\mathcal {C}$, the length of ![]() $M$ is finite and the endomorphism algebra of
$M$ is finite and the endomorphism algebra of ![]() $M$ has finite dimension over
$M$ has finite dimension over ![]() $k$. Assume that
$k$. Assume that ![]() $F$ sends semisimple objects of
$F$ sends semisimple objects of ![]() $\mathcal {C}$ to semisimple objects of
$\mathcal {C}$ to semisimple objects of ![]() $\mathcal {D}$. Then, the essential image of
$\mathcal {D}$. Then, the essential image of ![]() $F$ is closed under subquotients in
$F$ is closed under subquotients in ![]() $\mathcal {D}$.
$\mathcal {D}$.
Remark 8.9 Let ![]() $X$ be a smooth variety over
$X$ be a smooth variety over ![]() $k$. Let
$k$. Let ![]() $\mathcal {M}$ be a holonomic
$\mathcal {M}$ be a holonomic ![]() $\mathcal {D}_X$-module. Then
$\mathcal {D}_X$-module. Then ![]() $\mathcal {M}$ has finite length. Furthermore, the space
$\mathcal {M}$ has finite length. Furthermore, the space
is finite dimensional over ![]() $k$ as a consequence of Proposition 1.10.
$k$ as a consequence of Proposition 1.10.
Theorem 8.10 Let ![]() $(X,D)$ be a connected projective simple normal crossing pair of dimension at least
$(X,D)$ be a connected projective simple normal crossing pair of dimension at least ![]() $2$ over
$2$ over ![]() $k$. Assume that
$k$. Assume that ![]() $k$ is uncountable and algebraically closed. Let
$k$ is uncountable and algebraically closed. Let ![]() $\mathcal {L}$ be an ample line bundle on
$\mathcal {L}$ be an ample line bundle on ![]() $X$. Let
$X$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then, for every integer
$\operatorname {MIC}(X,D)$. Then, for every integer ![]() $m_1>0$, there is an integer
$m_1>0$, there is an integer ![]() $m> m_1$such that for every very generic hyperplane
$m> m_1$such that for every very generic hyperplane ![]() $H$ of
$H$ of ![]() $\mathcal {L}^m$ and every point
$\mathcal {L}^m$ and every point ![]() $x$ of
$x$ of ![]() $(X\setminus D)\cap H$, the induced morphism of differential Galois groups
$(X\setminus D)\cap H$, the induced morphism of differential Galois groups
is an isomorphism.
Proof. Let ![]() $m_1>0$. We have to show the existence of
$m_1>0$. We have to show the existence of ![]() $m>m_1$ such that for every very generic hyperplane
$m>m_1$ such that for every very generic hyperplane ![]() $H$ of
$H$ of ![]() $\mathcal {L}^m$, the functor
$\mathcal {L}^m$, the functor ![]() $F_H : \langle \mathcal {M} \rangle \to \langle \mathcal {M}|_{X\cap H}\rangle$ of neutralized Tannakian categories induced by the restriction to
$F_H : \langle \mathcal {M} \rangle \to \langle \mathcal {M}|_{X\cap H}\rangle$ of neutralized Tannakian categories induced by the restriction to ![]() $X\cap H$ is an equivalence. This amounts to show the existence of
$X\cap H$ is an equivalence. This amounts to show the existence of ![]() $m>m_1$ such that for every very generic
$m>m_1$ such that for every very generic ![]() $H$, the functor
$H$, the functor ![]() $F_H$ is fully faithful and its essential image is closed under taking subquotients. From Remark 8.9, Lemma 8.8 applies to
$F_H$ is fully faithful and its essential image is closed under taking subquotients. From Remark 8.9, Lemma 8.8 applies to ![]() $F_H$ and we are left to show the existence of
$F_H$ and we are left to show the existence of ![]() $m>m_1$ such that for every very generic
$m>m_1$ such that for every very generic ![]() $H$, the functor
$H$, the functor ![]() $F_H$ is fully faithful and sends semisimple objects to semisimple objects. This follows from Corollary 8.6 and Lemma 8.7.
$F_H$ is fully faithful and sends semisimple objects to semisimple objects. This follows from Corollary 8.6 and Lemma 8.7.
Acknowledgements
We thank N. Budur for pointing out the work of L. Xiao [Reference XiaoXia15]. We thank A. Langer for explaining to us the mismatch between Nitsure's construction and the expectation of what ![]() $\mathcal {M}_r(X,D,R)$ should be when
$\mathcal {M}_r(X,D,R)$ should be when ![]() $R=0$. We thank J. Sauloy for prompting the authors to look for genericity and not only existence of the hyperplanes from Theorem 0.3. We thank an anonymous referee for useful comments.
$R=0$. We thank J. Sauloy for prompting the authors to look for genericity and not only existence of the hyperplanes from Theorem 0.3. We thank an anonymous referee for useful comments.
Conflicts of interest
None.
Financial support
H.H. is supported by the National Natural Science Foundation of China (grant no. 11901287) and the Natural Science Foundation of Jiangsu Province (grant no. BK20190288).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.
Appendix A. Base field extension lemmas
The goal of this purely technical appendix is to prove various compatibilities with base field extension of some constructions considered in this paper.
A.1 Cohomological boundedness and base field extension
Lemma A.1 Let ![]() $d\geq 0$ be an integer. Let
$d\geq 0$ be an integer. Let ![]() $k$ be a field of characteristic
$k$ be a field of characteristic ![]() $0$. Then, cohomological boundedness holds in dimension
$0$. Then, cohomological boundedness holds in dimension ![]() $d$ over
$d$ over ![]() $k$ if it holds in dimension
$k$ if it holds in dimension ![]() $d$ over
$d$ over ![]() $\mathbb {C}$.
$\mathbb {C}$.
Proof. Let ![]() $(X,D)$ be a normal crossing pair over
$(X,D)$ be a normal crossing pair over ![]() $k$. Let
$k$. Let ![]() $R$ be an effective divisor of
$R$ be an effective divisor of ![]() $X$ supported on
$X$ supported on ![]() $D$. Let
$D$. Let ![]() $\kappa$ be a finitely generated extension of
$\kappa$ be a finitely generated extension of ![]() $\mathbb {Q}$ such that
$\mathbb {Q}$ such that ![]() $(X,D)$ descends to a normal crossing pair
$(X,D)$ descends to a normal crossing pair ![]() $(X_\kappa, D_\kappa )$. Put
$(X_\kappa, D_\kappa )$. Put ![]() $S:=(\operatorname {fdeg} R)\cdot D_\kappa$. Then,
$S:=(\operatorname {fdeg} R)\cdot D_\kappa$. Then, ![]() $R\leq S_k$ and
$R\leq S_k$ and ![]() $S$ depends linearly on
$S$ depends linearly on ![]() $R$. Choose an embedding
$R$. Choose an embedding ![]() $\kappa \to \mathbb {C}$. Let
$\kappa \to \mathbb {C}$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D,R)$. Then, there exists an intermediate extension
$\operatorname {MIC}(X,D,R)$. Then, there exists an intermediate extension ![]() $\kappa \subset \kappa _{\mathcal {M}}\subset k$ such that
$\kappa \subset \kappa _{\mathcal {M}}\subset k$ such that ![]() $\kappa _{\mathcal {M}}/\kappa$ is finitely generated and such that
$\kappa _{\mathcal {M}}/\kappa$ is finitely generated and such that ![]() $\mathcal {M}$ descends to an object
$\mathcal {M}$ descends to an object ![]() $\mathcal {M}_{\kappa _{\mathcal {M}}}$ of
$\mathcal {M}_{\kappa _{\mathcal {M}}}$ of ![]() $\operatorname {MIC}(X_{\kappa _{\mathcal {M}}},D_{\kappa _{\mathcal {M}}})$, where
$\operatorname {MIC}(X_{\kappa _{\mathcal {M}}},D_{\kappa _{\mathcal {M}}})$, where ![]() $(X_{\kappa _{\mathcal {M}}},D_{\kappa _{\mathcal {M}}})$ is the pull-back of
$(X_{\kappa _{\mathcal {M}}},D_{\kappa _{\mathcal {M}}})$ is the pull-back of ![]() $(X_{\kappa },D_{\kappa })$ over
$(X_{\kappa },D_{\kappa })$ over ![]() $\kappa _{\mathcal {M}}$. From Lemma 1.41, we have
$\kappa _{\mathcal {M}}$. From Lemma 1.41, we have
Thus,
Hence, ![]() $\mathcal {M}_{\kappa _{\mathcal {M}}}$ is an object of
$\mathcal {M}_{\kappa _{\mathcal {M}}}$ is an object of ![]() $\operatorname {MIC}(X_{\kappa _{\mathcal {M}}},D_{\kappa _{\mathcal {M}}},S_{\kappa _{\mathcal {M}}})$. Choose an embedding
$\operatorname {MIC}(X_{\kappa _{\mathcal {M}}},D_{\kappa _{\mathcal {M}}},S_{\kappa _{\mathcal {M}}})$. Choose an embedding ![]() $\kappa _{\mathcal {M}}\to \mathbb {C}$ over
$\kappa _{\mathcal {M}}\to \mathbb {C}$ over ![]() $\kappa$. Observe that the complex variety
$\kappa$. Observe that the complex variety
does not depend on ![]() $\kappa _{\mathcal {M}}$, and thus does not depend on
$\kappa _{\mathcal {M}}$, and thus does not depend on ![]() $\mathcal {M}$. Furthermore,
$\mathcal {M}$. Furthermore, ![]() $\mathbb {C}\times _{\kappa } D_{\kappa }$ is a normal crossing divisor and
$\mathbb {C}\times _{\kappa } D_{\kappa }$ is a normal crossing divisor and ![]() $\mathbb {C}\times _{\kappa } X_{\kappa }$ is projective over
$\mathbb {C}\times _{\kappa } X_{\kappa }$ is projective over ![]() $\mathbb {C}$ if
$\mathbb {C}$ if ![]() $X$ is projective over
$X$ is projective over ![]() $k$. Let us assume that
$k$. Let us assume that ![]() $X$ is projective of dimension
$X$ is projective of dimension ![]() $d$ over
$d$ over ![]() $k$. By assumption, let
$k$. By assumption, let ![]() $C : \operatorname {Div}(\mathbb {C}\times _{\kappa } X_{\kappa },\mathbb {C}\times _{\kappa } D_{\kappa })\oplus \mathbb {Z}\to \mathbb {Z}$ be a polynomial of degree at most
$C : \operatorname {Div}(\mathbb {C}\times _{\kappa } X_{\kappa },\mathbb {C}\times _{\kappa } D_{\kappa })\oplus \mathbb {Z}\to \mathbb {Z}$ be a polynomial of degree at most ![]() $d$ affine in the last variable such that cohomological boundedness holds for
$d$ affine in the last variable such that cohomological boundedness holds for ![]() $(\mathbb {C}\times _{\kappa } X_{\kappa },\mathbb {C}\times _{\kappa } D_{\kappa })$ with bound
$(\mathbb {C}\times _{\kappa } X_{\kappa },\mathbb {C}\times _{\kappa } D_{\kappa })$ with bound ![]() $C$. From Lemma 1.41, we know that
$C$. From Lemma 1.41, we know that ![]() $(\mathcal {M}_{\kappa _{\mathcal {M}}})_{\mathbb {C}}$ is an object of
$(\mathcal {M}_{\kappa _{\mathcal {M}}})_{\mathbb {C}}$ is an object of ![]() $\operatorname {MIC}(\mathbb {C}\times _{\kappa } X_{\kappa },\mathbb {C}\times _{\kappa } D_{\kappa },S_{\mathbb {C}})$ with
$\operatorname {MIC}(\mathbb {C}\times _{\kappa } X_{\kappa },\mathbb {C}\times _{\kappa } D_{\kappa },S_{\mathbb {C}})$ with ![]() $S_{\mathbb {C}}=(\operatorname {fdeg} R)\cdot (\mathbb {C}\times _{\kappa } D_{\kappa })$. From Remark 1.11, we deduce
$S_{\mathbb {C}}=(\operatorname {fdeg} R)\cdot (\mathbb {C}\times _{\kappa } D_{\kappa })$. From Remark 1.11, we deduce
and the proof of Lemma A.1 is complete.
A.2 Partial discrepancy and base field extension
The goal of this subsection is to prove Lemma A.6. Lemma A.6 is used to reduce the computation of the characteristic cycle of a connection on a surface to the case where the base field is ![]() $\mathbb {C}$.
$\mathbb {C}$.
Lemma A.2 Let ![]() $(X,D)$ be a geometrically connected normal crossing surface over
$(X,D)$ be a geometrically connected normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $k \subset K$ be a field extension. Let
$k \subset K$ be a field extension. Let ![]() $w$ be a divisorial valuation on
$w$ be a divisorial valuation on ![]() $X$ and let
$X$ and let ![]() $v$ be an extension of
$v$ be an extension of ![]() $w$ on
$w$ on ![]() $X_K$. Let
$X_K$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then,
$\operatorname {MIC}(X,D)$. Then,
Proof. Let ![]() $f : Y\to X$ be a modification of
$f : Y\to X$ be a modification of ![]() $X$ such that
$X$ such that ![]() $w$ is centred at a divisor
$w$ is centred at a divisor ![]() $E$ of
$E$ of ![]() $Y$. Then,
$Y$. Then, ![]() $v$ is centred at an irreducible component
$v$ is centred at an irreducible component ![]() $F$ of
$F$ of ![]() $E_K$. Let
$E_K$. Let ![]() $\eta _E$ be the generic point of
$\eta _E$ be the generic point of ![]() $E$ and let
$E$ and let ![]() $\eta _F$ be the generic point of
$\eta _F$ be the generic point of ![]() $F$. Observe that a uniformizer of
$F$. Observe that a uniformizer of ![]() $\mathcal {O}_{Y,\eta _E}$ pulls-back along
$\mathcal {O}_{Y,\eta _E}$ pulls-back along ![]() $Y_K\to Y$ to a uniformizer of
$Y_K\to Y$ to a uniformizer of ![]() $\mathcal {O}_{Y_K,\eta _F}$. Hence,
$\mathcal {O}_{Y_K,\eta _F}$. Hence, ![]() $\operatorname {irr}(F, f_K^+\mathcal {M}_K)=\operatorname {irr}(E,f^+\mathcal {M})$ and the equality
$\operatorname {irr}(F, f_K^+\mathcal {M}_K)=\operatorname {irr}(E,f^+\mathcal {M})$ and the equality ![]() $(\operatorname {Irr} \mathcal {M}_K)(v)=(\operatorname {Irr} \mathcal {M})(w)$ follows.
$(\operatorname {Irr} \mathcal {M}_K)(v)=(\operatorname {Irr} \mathcal {M})(w)$ follows.
Lemma A.3 Let ![]() $(X,D)$ be a geometrically connected normal crossing surface over
$(X,D)$ be a geometrically connected normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $k \subset K$ be a field extension. Let
$k \subset K$ be a field extension. Let ![]() $w$ be a divisorial valuation on
$w$ be a divisorial valuation on ![]() $X$ and let
$X$ and let ![]() $v$ be an extension of
$v$ be an extension of ![]() $w$ on
$w$ on ![]() $X_K$. Let
$X_K$. Let ![]() $\mathcal {M}$ be an object of
$\mathcal {M}$ be an object of ![]() $\operatorname {MIC}(X,D)$. Then,
$\operatorname {MIC}(X,D)$. Then,
Proof. If the centre of ![]() $w$ on
$w$ on ![]() $X$ is a divisor, then the centre of
$X$ is a divisor, then the centre of ![]() $v$ on
$v$ on ![]() $X_K$ is also a divisor. In that case,
$X_K$ is also a divisor. In that case, ![]() $(\delta \operatorname {Irr} \mathcal {M}_K)(v)=(\delta \operatorname {Irr} \mathcal {M})(w)=0$. Hence, we can suppose that
$(\delta \operatorname {Irr} \mathcal {M}_K)(v)=(\delta \operatorname {Irr} \mathcal {M})(w)=0$. Hence, we can suppose that ![]() $w$ is centred at a closed point of
$w$ is centred at a closed point of ![]() $X$. Then, there exists a modification
$X$. Then, there exists a modification ![]() $p : Y\to X$ of
$p : Y\to X$ of ![]() $X$ such that
$X$ such that ![]() $w$ is centred at a closed point
$w$ is centred at a closed point ![]() $P$ of
$P$ of ![]() $Y$ and
$Y$ and ![]() $w$ is centred at the exceptional divisor
$w$ is centred at the exceptional divisor ![]() $E$ of the blow-up
$E$ of the blow-up ![]() $Y'\to Y$ of
$Y'\to Y$ of ![]() $Y$ at
$Y$ at ![]() $P$. Then,
$P$. Then, ![]() $v$ is centred at a closed point
$v$ is centred at a closed point ![]() $Q$ of
$Q$ of ![]() $Y_K$ lying over
$Y_K$ lying over ![]() $P$. Let
$P$. Let ![]() $S\subset Y_K$ be the set of closed points of
$S\subset Y_K$ be the set of closed points of ![]() $Y_K$ lying over
$Y_K$ lying over ![]() $P$. Let
$P$. Let ![]() $Y_K'$ be the blow-up of
$Y_K'$ be the blow-up of ![]() $Y_K$ at
$Y_K$ at ![]() $S$. Since blowing-up commutes with flat base change, there is the following canonical cartesian diagram of varieties.
$S$. Since blowing-up commutes with flat base change, there is the following canonical cartesian diagram of varieties.

Hence, ![]() $v$ is centred at the exceptional divisor
$v$ is centred at the exceptional divisor ![]() $F$ of
$F$ of ![]() $Y_K'$ lying over
$Y_K'$ lying over ![]() $Q$. Thus, Proposition 4.11 applies to
$Q$. Thus, Proposition 4.11 applies to ![]() $v$ and
$v$ and ![]() $w$. Consider the following cartesian diagram.
$w$. Consider the following cartesian diagram.

Since ![]() $X_K\to X$ is étale, so is the map
$X_K\to X$ is étale, so is the map ![]() $f^*_K D_K\to f^*D$. In particular, the point
$f^*_K D_K\to f^*D$. In particular, the point ![]() $Q$ is a singular point of
$Q$ is a singular point of ![]() $f^*_K D_K$ if and only if
$f^*_K D_K$ if and only if ![]() $P$ is a singular point of
$P$ is a singular point of ![]() $f^*D$. Thus, if
$f^*D$. Thus, if ![]() $Q$ is a singular point of
$Q$ is a singular point of ![]() $f^*_K D_K$, we have
$f^*_K D_K$, we have
Otherwise,
 \begin{align*} (\delta \operatorname{Irr} \mathcal{M}_K)(v) & = ((\operatorname{Irr} \mathcal{M}_K)(Y_K))(v)-(\operatorname{Irr} \mathcal{M}_K)(v) \\ & =((\operatorname{Irr} \mathcal{M})(Y))(w)-(\operatorname{Irr} \mathcal{M})(w)\\ & =(\delta\operatorname{Irr} \mathcal{M})(w), \end{align*}
\begin{align*} (\delta \operatorname{Irr} \mathcal{M}_K)(v) & = ((\operatorname{Irr} \mathcal{M}_K)(Y_K))(v)-(\operatorname{Irr} \mathcal{M}_K)(v) \\ & =((\operatorname{Irr} \mathcal{M})(Y))(w)-(\operatorname{Irr} \mathcal{M})(w)\\ & =(\delta\operatorname{Irr} \mathcal{M})(w), \end{align*}
where the second equality follows from Lemma A.2. Lemma A.3 is thus proved.
Lemma A.4 Let ![]() $(X,D)$ be a geometrically connected normal crossing surface over
$(X,D)$ be a geometrically connected normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $k \subset K$ be a field extension. Let
$k \subset K$ be a field extension. Let ![]() $P$ be any point of
$P$ be any point of ![]() $X$. Let
$X$. Let ![]() $Q$ be a point of
$Q$ be a point of ![]() $X_K$ lying over
$X_K$ lying over ![]() $P$. Then,
$P$. Then,
Proof. Every divisorial valuation on ![]() $X$ centred at
$X$ centred at ![]() $P$ admits an extension to a divisorial valuation on
$P$ admits an extension to a divisorial valuation on ![]() $X_K$ centred at
$X_K$ centred at ![]() $Q$. Then, Lemma A.4 follows from Lemma A.3.
$Q$. Then, Lemma A.4 follows from Lemma A.3.
Lemma A.5 Let ![]() $(X,D)$ be a connected normal crossing surface over
$(X,D)$ be a connected normal crossing surface over ![]() $k$. Assume that
$k$. Assume that ![]() $k$ is algebraically closed. Let
$k$ is algebraically closed. Let ![]() $k \subset K$ be a field extension. Let
$k \subset K$ be a field extension. Let ![]() $P$ be a rational point of
$P$ be a rational point of ![]() $X/k$. Let
$X/k$. Let ![]() $Q$ be the unique rational point of
$Q$ be the unique rational point of ![]() $X_K/K$ lying over
$X_K/K$ lying over ![]() $P$. Then
$P$. Then
Proof. Let ![]() $f: Y\to X$ be a modification such that
$f: Y\to X$ be a modification such that ![]() $f^+\mathcal {M}$ has good formal structure. In particular,
$f^+\mathcal {M}$ has good formal structure. In particular, ![]() $f^+_K\mathcal {M}_K$ has good formal structure. Thus,
$f^+_K\mathcal {M}_K$ has good formal structure. Thus, ![]() $\operatorname {Irr} \mathcal {M}=\operatorname {Irr}(Y,f^+\mathcal {M})$ in
$\operatorname {Irr} \mathcal {M}=\operatorname {Irr}(Y,f^+\mathcal {M})$ in ![]() $\textbf {Div}(X)$ and
$\textbf {Div}(X)$ and ![]() $\operatorname {Irr} \mathcal {M}_K=\operatorname {Irr}(Y_K,f^+_K\mathcal {M}_K)$ in
$\operatorname {Irr} \mathcal {M}_K=\operatorname {Irr}(Y_K,f^+_K\mathcal {M}_K)$ in ![]() $\textbf {Div}(X_K)$. Hence, Proposition 4.15 ensures that
$\textbf {Div}(X_K)$. Hence, Proposition 4.15 ensures that ![]() $\delta \operatorname {Irr} \mathcal {M}$ is supported on the set
$\delta \operatorname {Irr} \mathcal {M}$ is supported on the set ![]() $A$ of divisorial valuations associated with the irreducible components of
$A$ of divisorial valuations associated with the irreducible components of ![]() $f^*D$. Similarly,
$f^*D$. Similarly, ![]() $\delta \operatorname {Irr} \mathcal {M}_K$ is supported on the set
$\delta \operatorname {Irr} \mathcal {M}_K$ is supported on the set ![]() $B$ of divisorial valuations associated with the irreducible components of
$B$ of divisorial valuations associated with the irreducible components of ![]() $f^*_K D_K$. Let
$f^*_K D_K$. Let ![]() $F$ be an irreducible component of
$F$ be an irreducible component of ![]() $f^*D$. Since
$f^*D$. Since ![]() $k$ is algebraically closed,
$k$ is algebraically closed, ![]() $F$ is geometrically irreducible. Thus,
$F$ is geometrically irreducible. Thus, ![]() $F_K$ is irreducible. Hence, the map
$F_K$ is irreducible. Hence, the map ![]() $f^*_K D_K\to f^*D$ induces a bijection on the sets of irreducible components. Thus, the map
$f^*_K D_K\to f^*D$ induces a bijection on the sets of irreducible components. Thus, the map ![]() $B\to A$ induced by restriction is bijective. Let
$B\to A$ induced by restriction is bijective. Let ![]() $A_P$ be the subset of
$A_P$ be the subset of ![]() $A$ of valuations centred at
$A$ of valuations centred at ![]() $P$ on
$P$ on ![]() $X$. Let
$X$. Let ![]() $B_Q$ be the subset of
$B_Q$ be the subset of ![]() $B$ of valuations centred at
$B$ of valuations centred at ![]() $Q$ on
$Q$ on ![]() $X_K$. Then, the bijection
$X_K$. Then, the bijection ![]() $B\to A$ induces a bijection
$B\to A$ induces a bijection ![]() $B_Q\to A_P$. Hence,
$B_Q\to A_P$. Hence,
 \[ \int_P \delta\operatorname{Irr} \mathcal{M} = \sum_{w\in A_P}(\delta\operatorname{Irr} \mathcal{M} )(w)= \sum_{v\in B_Q}(\delta\operatorname{Irr} \mathcal{M}_K )(v) = \int_Q \delta\operatorname{Irr} \mathcal{M}_K, \]
\[ \int_P \delta\operatorname{Irr} \mathcal{M} = \sum_{w\in A_P}(\delta\operatorname{Irr} \mathcal{M} )(w)= \sum_{v\in B_Q}(\delta\operatorname{Irr} \mathcal{M}_K )(v) = \int_Q \delta\operatorname{Irr} \mathcal{M}_K, \]
where the second equality follows from Lemma A.3. Lemma A.6 is thus proved.
Lemma A.6 Let ![]() $(X,D)$ be a geometrically connected normal crossing surface over
$(X,D)$ be a geometrically connected normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $k \subset K_1$ and
$k \subset K_1$ and ![]() $k \subset K_2$ be field extensions where
$k \subset K_2$ be field extensions where ![]() $K_1$ and
$K_1$ and ![]() $K_2$ are algebraically closed. Let
$K_2$ are algebraically closed. Let ![]() $P$ be a closed point of
$P$ be a closed point of ![]() $X$. For
$X$. For ![]() $i=1,2$, let
$i=1,2$, let ![]() $Q_i$ be a rational point of
$Q_i$ be a rational point of ![]() $X_{K_i}/K_i$ lying over
$X_{K_i}/K_i$ lying over ![]() $P$. Then,
$P$. Then,
Proof. For ![]() $i=1,2$, let
$i=1,2$, let ![]() $k_i$ be the algebraic closure of
$k_i$ be the algebraic closure of ![]() $k$ in
$k$ in ![]() $K_i$. Since
$K_i$. Since ![]() $K_1$ and
$K_1$ and ![]() $K_2$ are algebraically closed,
$K_2$ are algebraically closed, ![]() $k_1$ and
$k_1$ and ![]() $k_2$ are isomorphic over
$k_2$ are isomorphic over ![]() $k$. Let
$k$. Let ![]() $P_i$ be the image of
$P_i$ be the image of ![]() $Q_i$ via
$Q_i$ via ![]() $X_{K_i}\to X_{k_i}$. Consider the following commutative diagram over
$X_{K_i}\to X_{k_i}$. Consider the following commutative diagram over ![]() $k$.
$k$.

Choose an isomorphism between ![]() $k_1$ and
$k_1$ and ![]() $k_2$ over
$k_2$ over ![]() $k$. Let
$k$. Let ![]() $P_{21}$ be the pull-back of
$P_{21}$ be the pull-back of ![]() $P_2$ along the induced isomorphism
$P_2$ along the induced isomorphism ![]() $X_{k_1}\to X_{k_2}$. Then,
$X_{k_1}\to X_{k_2}$. Then,
Since ![]() $P_{21}$ and
$P_{21}$ and ![]() $P_1$ are two rational points of
$P_1$ are two rational points of ![]() $X_{k_1}/k_1$ lying over
$X_{k_1}/k_1$ lying over ![]() $P$, there exists an automorphism
$P$, there exists an automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $k_1$ over
$k_1$ over ![]() $k$ such that
$k$ such that ![]() $\sigma (P_{1})=P_{21}$. Thus,
$\sigma (P_{1})=P_{21}$. Thus,
From Lemma A.5, we deduce
and Lemma A.6 is proved.
Remark A.7 Applying Lemma A.6 to the case where ![]() $K_1=K_2=K$, we conclude that the integral
$K_1=K_2=K$, we conclude that the integral ![]() $\int _{Q} \delta \operatorname {Irr} \mathcal {M}_{K}$ does not depend on the choice of a rational point
$\int _{Q} \delta \operatorname {Irr} \mathcal {M}_{K}$ does not depend on the choice of a rational point ![]() $Q$ of
$Q$ of ![]() $X_{K}/K$ lying over
$X_{K}/K$ lying over ![]() $P$.
$P$.
Lemma A.8 Let ![]() $(X,D)$ be a geometrically connected normal crossing surface over
$(X,D)$ be a geometrically connected normal crossing surface over ![]() $k$. Let
$k$. Let ![]() $k \subset K_1$ and
$k \subset K_1$ and ![]() $k \subset K_2$ be field extensions where
$k \subset K_2$ be field extensions where ![]() $K_1$ and
$K_1$ and ![]() $K_2$ are algebraically closed. Let
$K_2$ are algebraically closed. Let ![]() $Z$ be a locally closed subset of
$Z$ be a locally closed subset of ![]() $X$. Then
$X$. Then
Proof. We are going to use Lemma A.6. We first argue that the points of ![]() $Z_{K_1}$ and
$Z_{K_1}$ and ![]() $Z_{K_2}$ not sent to a closed point of
$Z_{K_2}$ not sent to a closed point of ![]() $Z$ do not contribute to the above integrals. From Remark 1.29, we have
$Z$ do not contribute to the above integrals. From Remark 1.29, we have ![]() $\operatorname {TL}(\mathcal {M}_{K_1})=\operatorname {TL}(\mathcal {M})_{K_1}$. Hence, Lemma 5.12 yields
$\operatorname {TL}(\mathcal {M}_{K_1})=\operatorname {TL}(\mathcal {M})_{K_1}$. Hence, Lemma 5.12 yields
Since ![]() $\operatorname {TL}(\mathcal {M})$ is a finite set of closed points of
$\operatorname {TL}(\mathcal {M})$ is a finite set of closed points of ![]() $X$, so is
$X$, so is ![]() $Z\cap \operatorname {TL}(\mathcal {M})$. In particular,
$Z\cap \operatorname {TL}(\mathcal {M})$. In particular, ![]() $(Z\cap \operatorname {TL}(\mathcal {M}))_{K_1}$ is a finite set of rational points of
$(Z\cap \operatorname {TL}(\mathcal {M}))_{K_1}$ is a finite set of rational points of ![]() $X_{K_1}$ lying above closed points of
$X_{K_1}$ lying above closed points of ![]() $X$. For every point
$X$. For every point ![]() $P$ of
$P$ of ![]() $Z\cap \operatorname {TL}(\mathcal {M})$, choose a rational point
$Z\cap \operatorname {TL}(\mathcal {M})$, choose a rational point ![]() $Q_1(P)$ of
$Q_1(P)$ of ![]() $X_{K_1}$ above
$X_{K_1}$ above ![]() $P$ and let us denote by
$P$ and let us denote by ![]() $\deg P$ the degree of
$\deg P$ the degree of ![]() $P$ over
$P$ over ![]() $k$. Since
$k$. Since ![]() $K_1$ is algebraically closed,
$K_1$ is algebraically closed, ![]() $X_{K_1}$ admits exactly
$X_{K_1}$ admits exactly ![]() $\deg P$ rational points above
$\deg P$ rational points above ![]() $P$. From Remark A.7, we deduce
$P$. From Remark A.7, we deduce
 \[ \int_{Z_{K_1}} \delta\operatorname{Irr} \mathcal{M}_{K_1} = \sum_{Q_1\in(Z\cap \operatorname{TL}(\mathcal{M}))_{K_1} } \int_{Q_1} \delta\operatorname{Irr} \mathcal{M}_{K_1}= \sum_{P\in Z\cap \operatorname{TL}(\mathcal{M})} \deg P \cdot \int_{Q_1(P)} \delta\operatorname{Irr} \mathcal{M}_{K_1}. \]
\[ \int_{Z_{K_1}} \delta\operatorname{Irr} \mathcal{M}_{K_1} = \sum_{Q_1\in(Z\cap \operatorname{TL}(\mathcal{M}))_{K_1} } \int_{Q_1} \delta\operatorname{Irr} \mathcal{M}_{K_1}= \sum_{P\in Z\cap \operatorname{TL}(\mathcal{M})} \deg P \cdot \int_{Q_1(P)} \delta\operatorname{Irr} \mathcal{M}_{K_1}. \]
Since the same formula holds with ![]() $K_2$, Lemma A.8 follows from Lemma A.6.
$K_2$, Lemma A.8 follows from Lemma A.6.