Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-21T09:34:18.758Z Has data issue: false hasContentIssue false
  • English
  • Français

Burgess-like subconvexity for 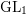$\text{GL}_{1}$

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  04 July 2019

Han Wu
Han Wu*
Affiliation:
MA C3 604, EPFL SB MATHGEOM TAN, CH-1015, Lausanne, Switzerland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize our previous method on the subconvexity problem for 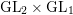$\text{GL}_{2}\times \text{GL}_{1}$ with cuspidal representations to Eisenstein series, and deduce a Burgess-like subconvex bound for Hecke characters, that is, the bound 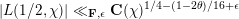$|L(1/2,\unicode[STIX]{x1D712})|\ll _{\mathbf{F},\unicode[STIX]{x1D716}}\mathbf{C}(\unicode[STIX]{x1D712})^{1/4-(1-2\unicode[STIX]{x1D703})/16+\unicode[STIX]{x1D716}}$ for varying Hecke characters 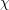$\unicode[STIX]{x1D712}$ over a number field 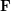$\mathbf{F}$ with analytic conductor 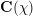$\mathbf{C}(\unicode[STIX]{x1D712})$. As a main tool, we apply the extended theory of regularized integrals due to Zagier developed in a previous paper to obtain the relevant triple product formulas of Eisenstein series.

Keywords

subconvexityL-function over number fieldBurgess-type hybrid bound

MSC classification

Primary: 11R42: Zeta functions and $L$-functions of number fields
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 8 , August 2019 , pp. 1457 - 1499
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partially supported by SNF-grant 200021-125291 and DFG-SNF-grant 00021L_153647.

References

Blomer, V. and Harcos, G., The spectral decomposition of shifted convolution sums , Duke Math. J. 144 (2008), 321–339.Google Scholar
Blomer, V. and Harcos, G., Twisted L-functions over number fields and Hilbert’s eleventh problem , Geom. Funct. Anal. 20 (2010), 1–52.Google Scholar
Bump, D., Automorphic forms and representations, Cambridge Studies in Advanced Mathematics, vol. 55 (Cambridge University Press, Cambridge, 1998).Google Scholar
Burgess, D., On character sums and L-series II , Proc. Lond. Math. Soc. (3) 13 (1963), 524–536.Google Scholar
Conrey, J. B. and Iwaniec, H., The cubic moment of central values of automorphic L-functions , Ann. of Math. (2) 151 (2000), 1175–1216.Google Scholar
Duke, W., Hyperbolic distribution problems and half-integral weight Maass forms , Invent. Math. 92 (1988), 73–90.Google Scholar
Duke, W., Friedlander, J. B. and Iwaniec, H., The subconvexity problem for Artin L-functions , Invent. Math. 149 (2002), 489–577.Google Scholar
Gelbart, S. S. and Jacquet, H., Forms of GL(2) from the analytic point of view , Proc. Sympos. Pure Math. 33 (1979), 213–251.Google Scholar
Heath-Brown, D., Hybrid bounds for Dirichlet L-functions , Invent. Math. 47 (1978), 149–170.Google Scholar
Heath-Brown, D., Hybrid bounds for Dirichlet L-functions II , Q. J. Math. (2) 31 (1980), 157–167.Google Scholar
Huxley, M. and Watt, N., Hybrid bounds for Dirichlet’s L-function , Math. Proc. Cambridge Philos. Soc. 129 (2000), 385–415.Google Scholar
Jacquet, H., Integral representation of Whittaker functions , in Contributions to automorphic forms, geometry and number theory, eds Hida, H., Ramakrishnan, D. and Shahidi, F. (Johns Hopkins University Press, Baltimore, MD, 2004), 373–419, ch. 15.Google Scholar
Michel, P., Analytic number theory and families of automorphic L-functions , in Automorphic forms and applications, IAS/Park City Mathematics Series, vol. 12 (American Mathematical Society, Providence, RI, 2007), 181–295.Google Scholar
Michel, P. and Venkatesh, A., The subconvexity problem for GL2 , Publ. Math. Inst. Hautes Études Sci. 111 (2010), 171–271.Google Scholar
Milićević, D., Sub-Weyl subconvexity for Dirichlet L-functions to prime power moduli , Compositio Math. 152 (2016), 825–875.Google Scholar
Patterson, S., An introduction to the theory of the Riemann zeta-function, Cambridge Studies in Advanced Mathematics, vol. 14 (Cambridge University Press, Cambridge, 1988).Google Scholar
Petrow, I. and Young, M. P., A generalized cubic moment and the Petersson formula for newforms , Math. Ann. 373 (2018), 287–353.Google Scholar
Rudin, W., Real and complex analysis, third edition (Tata McGraw-Hill, New Delhi, 1986).Google Scholar
Sarnak, P., Estimates for Ranking–Selberg L-functions and quantum unique ergodicity , J. Funct. Anal. 184 (2001), 419–453.Google Scholar
Soehne, P., An upper bound for Hecke zeta-functions with Groessencharacters , J. Number Theory 66 (1997), 225–250, NT972167.Google Scholar
Weyl, H., Zur Abschätzung von 𝜁(1 + ti) , Math. Z. 10 (1921), 88–101.Google Scholar
Wu, H., Burgess-like subconvex bounds for GL2 × GL1 , Geom. Funct. Anal. 24 (2014), 968–1036.Google Scholar
Wu, H., Explicit Burgess-like subconvex bounds for $\text{GL}_{2}\times \text{GL}_{1}$ , Preprint (2017), arXiv:1712.04365.Google Scholar
Wu, H., A note on spectral analysis in automorphic representation theory for GL2 : I , Int. J. Number Theory 13 (2017), 2717–2750.Google Scholar
Wu, H., Deducing Selberg trace formula via Rankin–Selberg method for $\text{GL}_{2}$ . Trans. Amer. Math. Soc., to appear. Preprint (2018), arXiv:1810.09437.Google Scholar
Young, M. P., Weyl-type hybrid subconvexity bounds for twisted L-functions and Heegner points on shrinking sets , J. Eur. Math. Soc. (JEMS) 19 (2017), 1545–1576.Google Scholar
Zagier, D., The Rankin–Selberg method for automorphic functions which are not of rapid decay , J. Fac. Sci. 28 (1982), 415–438.Google Scholar