Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
KUMAR, SHRAWAN
2014.
A SURVEY OF THE ADDITIVE EIGENVALUE PROBLEM (WITH APPENDIX BY M. KAPOVICH).
Transformation Groups,
Vol. 19,
Issue. 4,
p.
1051.
Fontaine, Bruce
and
Kamnitzer, Joel
2014.
Cyclic sieving, rotation, and geometric representation theory.
Selecta Mathematica,
Vol. 20,
Issue. 2,
p.
609.
Mackaay, M.
Pan, W.
and
Tubbenhauer, D.
2014.
The $$\mathfrak {sl}_{3}$$ sl 3 -web algebra.
Mathematische Zeitschrift,
Vol. 277,
Issue. 1-2,
p.
401.
Hong, Jiuzu
and
Shen, Linhui
2015.
Tensor invariants, saturation problems, and Dynkin automorphisms.
Advances in Mathematics,
Vol. 285,
Issue. ,
p.
629.
Housley, Matthew
Russell, Heather M.
and
Tymoczko, Julianna
2015.
The Robinson–Schensted correspondence and $$A_2$$ A 2 -web bases.
Journal of Algebraic Combinatorics,
Vol. 42,
Issue. 1,
p.
293.
Le, Ian
2016.
Higher laminations and affine buildings.
Geometry & Topology,
Vol. 20,
Issue. 3,
p.
1673.
Helm, David
Tian, Yichao
and
Xiao, Liang
2017.
Tate cycles on some unitary Shimura varieties
mod p.
Algebra & Number Theory,
Vol. 11,
Issue. 10,
p.
2213.
Cautis, Sabin
and
Kamnitzer, Joel
2018.
Quantum K-theoretic geometric Satake: the case.
Compositio Mathematica,
Vol. 154,
Issue. 2,
p.
275.
Russell, Heather M
and
Tymoczko, Julianna S
2019.
The Transition Matrix between the Specht and Web Bases Is Unipotent with Additional Vanishing Entries.
International Mathematics Research Notices,
Vol. 2019,
Issue. 5,
p.
1479.
Frohman, Charles
2019.
Spider evaluation and representations of web groups.
Journal of Knot Theory and Its Ramifications,
Vol. 28,
Issue. 04,
p.
1950021.
Lamberti, Lisa
2020.
Tensor Diagrams and Chebyshev Polynomials.
International Mathematics Research Notices,
Vol. 2020,
Issue. 20,
p.
7218.
Zhang, Leon
2021.
Computing Min-Convex Hulls in the Affine Building of $$\hbox {SL}_d$$.
Discrete & Computational Geometry,
Vol. 65,
Issue. 4,
p.
1314.
Baumann, Pierre
and
Demarais, Arnaud
2021.
Mirković–Vilonen basis in type 𝐴₁.
Representation Theory of the American Mathematical Society,
Vol. 25,
Issue. 27,
p.
780.
Russell, Heather M
and
Tymoczko, Julianna
2022.
The Transition Matrix Between the Specht and 𝔰𝔩3 Web Bases is Unitriangular With Respect to Shadow Containment.
International Mathematics Research Notices,
Vol. 2022,
Issue. 5,
p.
3371.
Douglas, Daniel C.
and
Sun, Zhe
2024.
Tropical Fock–Goncharov coordinates for -webs on surfaces I: construction.
Forum of Mathematics, Sigma,
Vol. 12,
Issue. ,
Douglas, Daniel C.
and
Sun, Zhe
2025.
Tropical Fock–Goncharov coordinates for SL 3 -webs on surfaces II: naturality.
Algebraic Combinatorics,
Vol. 8,
Issue. 1,
p.
101.
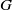 $G$ be a simple algebraic group. Labelled trivalent graphs called webs can be used to produce invariants in tensor products of minuscule representations. For each web, we construct a configuration space of points in the affine Grassmannian. Via the geometric Satake correspondence, we relate these configuration spaces to the invariant vectors coming from webs. In the case of
$G$ be a simple algebraic group. Labelled trivalent graphs called webs can be used to produce invariants in tensor products of minuscule representations. For each web, we construct a configuration space of points in the affine Grassmannian. Via the geometric Satake correspondence, we relate these configuration spaces to the invariant vectors coming from webs. In the case of 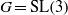 $G= \mathrm{SL} (3)$, non-elliptic webs yield a basis for the invariant spaces. The non-elliptic condition, which is equivalent to the condition that the dual diskoid of the web is
$G= \mathrm{SL} (3)$, non-elliptic webs yield a basis for the invariant spaces. The non-elliptic condition, which is equivalent to the condition that the dual diskoid of the web is  $\mathrm{CAT} (0)$, is explained by the fact that affine buildings are
$\mathrm{CAT} (0)$, is explained by the fact that affine buildings are 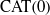 $\mathrm{CAT} (0)$.
$\mathrm{CAT} (0)$.

