Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T15:32:27.210Z Has data issue: false hasContentIssue false
  • English
  • Français

Brauer groups and Galois cohomology of commutative ring spectra

Part of: Division rings and semisimple Artin rings Operations and obstructions Homotopy theory Homological methods (field theory)

Published online by Cambridge University Press:  04 June 2021

David Gepner  and
Tyler Lawson
David Gepner
Affiliation:
Department of Mathematics, Statistics, and Computer Science, The University of Illinois at Chicago, 851 S. Morgan Street, 322 Science and Engineering Offices (M/C 249), Chicago, IL60607, [email protected]
Tyler Lawson
Affiliation:
School of Mathematics, The University of Minnesota, 206 Church St SE, Minneapolis, MN55455, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we develop methods for classifying Baker, Richter, and Szymik's Azumaya algebras over a commutative ring spectrum, especially in the largely inaccessible case where the ring is nonconnective. We give obstruction-theoretic tools, constructing and classifying these algebras and their automorphisms with Goerss–Hopkins obstruction theory, and give descent-theoretic tools, applying Lurie's work on 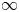$\infty$-categories to show that a finite Galois extension of rings in the sense of Rognes becomes a homotopy fixed-point equivalence on Brauer spaces. For even-periodic ring spectra 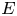$E$, we find that the ‘algebraic’ Azumaya algebras whose coefficient ring is projective are governed by the Brauer–Wall group of 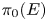$\pi _0(E)$, recovering a result of Baker, Richter, and Szymik. This allows us to calculate many examples. For example, we find that the algebraic Azumaya algebras over Lubin–Tate spectra have either four or two Morita equivalence classes, depending on whether the prime is odd or even, that all algebraic Azumaya algebras over the complex K-theory spectrum 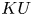$KU$ are Morita trivial, and that the group of the Morita classes of algebraic Azumaya algebras over the localization 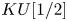$KU[1/2]$ is $\mathbb {Z}/8\times \mathbb {Z}/2$. Using our descent results and an obstruction theory spectral sequence, we also study Azumaya algebras over the real K-theory spectrum 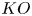$KO$ which become Morita-trivial 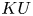$KU$-algebras. We show that there exist exactly two Morita equivalence classes of these. The nontrivial Morita equivalence class is realized by an ‘exotic’ 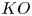$KO$-algebra with the same coefficient ring as 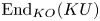$\mathrm {End}_{KO}(KU)$. This requires a careful analysis of what happens in the homotopy fixed-point spectral sequence for the Picard space of 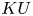$KU$, previously studied by Mathew and Stojanoska.

Keywords

Picard and Brauer groupsobstruction theoryGalois cohomology

MSC classification

Primary: 55P43: Spectra with additional structure ($E_infty$, $A_infty$, ring spectra, etc.) 55S35: Obstruction theory
Secondary: 12G05: Galois cohomology 16K50: Brauer groups
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 6 , June 2021 , pp. 1211 - 1264
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

D.G. was partially supported by NSF grants DMS-1406529 and DMS-1714273 and T.L. was partially supported by NSF grant DMS-1206008.

References

Adams, J. F., Prerequisites (on equivariant stable homotopy) for Carlsson's lecture, in Algebraic topology (Aarhus, 1982), Lecture Notes in Mathematics, vol. 1051 (Springer, Berlin, 1984), 483–532.CrossRefGoogle Scholar
Ando, M., Blumberg, A. J. and Gepner, D., Parametrized spectra, multiplicative Thom spectra, and the twisted Umkehr map, Geom. Topol. 22 (2018), 3761–3825.Google Scholar
Antieau, B. and Gepner, D., Brauer groups and étale cohomology in derived algebraic geometry, Geom. Topol. 18 (2014), 1149–1244.10.2140/gt.2014.18.1149CrossRefGoogle Scholar
Auslander, M. and Goldman, O., The Brauer group of a commutative ring, Trans. Amer. Math. Soc. 97 (1960), 367–409.10.1090/S0002-9947-1960-0121392-6CrossRefGoogle Scholar
Azumaya, G., On maximally central algebras, Nagoya Math. J. 2 (1951), 119–150.10.1017/S0027763000010114CrossRefGoogle Scholar
Baker, A., Richter, B. and Szymik, M., Brauer groups for commutative $S$-algebras, J. Pure Appl. Algebra 216 (2012), 2361–2376.CrossRefGoogle Scholar
Blumberg, A. J., Gepner, D. and Tabuada, G., Uniqueness of the multiplicative cyclotomic trace, Adv. Math. 260 (2014), 191–232.Google Scholar
Bousfield, A. K., Homotopy spectral sequences and obstructions, Israel J. Math. 66 (1989), 54–104.10.1007/BF02765886CrossRefGoogle Scholar
Bousfield, A. K., Cosimplicial resolutions and homotopy spectral sequences in model categories, Geom. Topol. 7 (2003), 1001–1053.10.2140/gt.2003.7.1001CrossRefGoogle Scholar
Childs, L. N., Garfinkel, G. and Orzech, M., The Brauer group of graded Azumaya algebras, Trans. Amer. Math. Soc. 175 (1973), 299–326.10.1090/S0002-9947-1973-0349652-3CrossRefGoogle Scholar
Davis, D. G. and Lawson, T., Commutative ring objects in pro-categories and generalized Moore spectra, Geom. Topol. 18 (2014), 103–140.CrossRefGoogle Scholar
Freed, D. S., Lectures on twisted K-theory and orientifolds, Preprint (2012), https://web.ma.utexas.edu/users/dafr/vienna.pdf.Google Scholar
Gepner, D. and Haugseng, R., Enriched $\infty$-categories via non-symmetric $\infty$-operads, Adv. Math. 279 (2015), 575–716.CrossRefGoogle Scholar
Goerss, P. G. and Hopkins, M. J., Moduli spaces of commutative ring spectra, in Structured ring spectra, London Mathematical Society Lecture Note Series, vol. 315 (Cambridge University Press, Cambridge, 2004), 151–200.10.1017/CBO9780511529955.009CrossRefGoogle Scholar
Goerss, P. G. and Hopkins, M. J., Moduli problems for structured ring spectra, Preprint, http://www.math.northwestern.edu/~pgoerss/spectra/obstruct.pdf.Google Scholar
Grothendieck, A., Le groupe de Brauer. I. Algèbres d'Azumaya et interprétations diverses, in Dix Exposés sur la Cohomologie des Schémas (North-Holland/Masson, Amsterdam/Paris, 1968), 46–66.Google Scholar
Haugseng, R., The higher Morita category of $E_n$-algebras, Geom. Topol. 21 (2017), 1631–1730.10.2140/gt.2017.21.1631CrossRefGoogle Scholar
Hopkins, M. and Lurie, J., On Brauer groups of Lubin-Tate spectra I, Preprint (2017), http://www.math.harvard.edu/~lurie/papers/Brauer.pdf.Google Scholar
Hopkins, M. J., Mahowald, M. and Sadofsky, H., Constructions of elements in Picard groups, in Topology and representation theory (Evanston, IL, 1992), Contemporary Mathematics, vol. 158 (American Mathematical Society, Providence, RI, 1994), 89–126.CrossRefGoogle Scholar
Hovey, M. and Strickland, N. P., Morava $K$-theories and localisation, Mem. Amer. Math. Soc. 139 (1999).Google Scholar
Ikai, H., Azumaya algebras with general gradings and their automorphisms, Tsukuba J. Math. 23 (1999), 293–320.CrossRefGoogle Scholar
Johnson, N., Azumaya objects in triangulated bicategories, J. Homotopy Relat. Struct. 9 (2014), 465–493.CrossRefGoogle Scholar
Johnson, N. and Osorno, A. M., Modeling stable one-types, Theory Appl. Categ. 26 (2012), 520–537.Google Scholar
Karoubi, M., Twisted bundles and twisted K-theory, in Topics in noncommutative geometry, Clay Mathematics Proceedings, vol. 16 (American Mathematical Society, Providence, RI, 2012), 223–257.Google Scholar
Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
Lurie, J., Derived algebraic geometry VIII: Quasi-coherent sheaves and Tannaka duality theorems, Preprint (2011), http://www.math.harvard.edu/~lurie/papers/DAG-VIII.pdf.Google Scholar
Lurie, J., Derived algebraic geometry VII: Spectral schemes, Preprint (2011), http://www.math.harvard.edu/~lurie/papers/DAG-VII.pdf.Google Scholar
Lurie, J., Higher algebra, Preprint (2017), https://www.math.ias.edu/~lurie/papers/HA.pdf.Google Scholar
Lurie, J., Spectral algebraic geometry, Preprint (2018), https://www.math.ias.edu/~lurie/papers/SAG-rootfile.pdf.Google Scholar
Mathew, A., The Galois group of a stable homotopy theory, Adv. Math. 291 (2016), 403–541.CrossRefGoogle Scholar
Mathew, A., Residue fields for a class of rational $\mathbf {E}_\infty$-rings and applications, J. Pure Appl. Algebra 221 (2017), 707–748.CrossRefGoogle Scholar
Mathew, A. and Stojanoska, V., The Picard group of topological modular forms via descent theory, Geom. Topol. 20 (2016), 3133–3217.CrossRefGoogle Scholar
Pstragowski, P. and VanKoughnett, P., Abstract Goerss-Hopkins obstruction theory, Preprint (2019), arXiv:1904.08881.Google Scholar
Quillen, D., On the (co-)homology of commutative rings, in Applications of categorical algebra, Proceedings of Symposia in Pure Mathematics, vol. XVII (American Mathematical Society, Providence, RI, 1970), 65–87.CrossRefGoogle Scholar
Rognes, J., Galois extensions of structured ring spectra. Stably dualizable groups, Mem. Amer. Math. Soc. 192 (2008).Google Scholar
Rosenberg, A. and Zelinsky, D., Automorphisms of separable algebras, Pacific J. Math. 11 (1961), 1109–1117.CrossRefGoogle Scholar
Schwede, S. and Shipley, B. E., Algebras and modules in monoidal model categories, Proc. Lond. Math. Soc. (3) 80 (2000), 491–511.CrossRefGoogle Scholar
Schwede, S. and Shipley, B., Stable model categories are categories of modules, Topology 42 (2003), 103–153.CrossRefGoogle Scholar
Shipley, B., A convenient model category for commutative ring spectra, in Homotopy theory: relations with algebraic geometry, group cohomology, and algebraic K-theory, Contemporary Mathematics, vol. 346 (American Mathematical Society, Providence, RI, 2004), 473–483.Google Scholar
Small, C., The Brauer-Wall group of a commutative ring, Trans. Amer. Math. Soc. 156 (1971), 455–491.CrossRefGoogle Scholar
Toën, B., Derived Azumaya algebras and generators for twisted derived categories, Invent. Math. 189 (2012), 581–652.CrossRefGoogle Scholar
Wall, C. T. C., Graded Brauer groups, J. Reine Angew. Math. 213 (1964), 187–199.Google Scholar