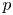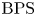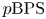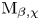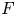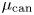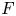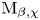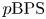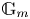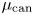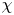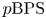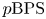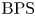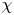1. Introduction
Donaldson–Thomas (DT) invariants, first introduced in [Reference ThomasTho00], count stable sheaves with some fixed Chern character ![]() $\gamma \in H^*(X,\mathbb {Z})$ on a smooth Calabi–Yau 3-fold
$\gamma \in H^*(X,\mathbb {Z})$ on a smooth Calabi–Yau 3-fold ![]() $X$. While with the original machinery the invariants could only be defined for moduli of sheaves where no strictly semi-stables occur, Joyce and Song [Reference Joyce and SongJS12] and Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS08] independently developed a generalized theory allowing the definition of DT invariants for moduli of objects (in CY3 categories) also in those cases where strictly semi-stables are present. The two approaches have some differences and the resulting generalized numerical invariants, denoted in the above references by
$X$. While with the original machinery the invariants could only be defined for moduli of sheaves where no strictly semi-stables occur, Joyce and Song [Reference Joyce and SongJS12] and Kontsevich and Soibelman [Reference Kontsevich and SoibelmanKS08] independently developed a generalized theory allowing the definition of DT invariants for moduli of objects (in CY3 categories) also in those cases where strictly semi-stables are present. The two approaches have some differences and the resulting generalized numerical invariants, denoted in the above references by ![]() $\bar {{\rm DT}}_{\gamma }$ and
$\bar {{\rm DT}}_{\gamma }$ and ![]() $\hat {{\rm DT}}_{\gamma }$ or
$\hat {{\rm DT}}_{\gamma }$ or ![]() $\Omega (\gamma )$ respectively do not coincide. The relation between the two is however understood and explained for example in [Reference Joyce and SongJS12, § 6.2] or [Reference Davison and MeinhardtDM15, § 6.7].
$\Omega (\gamma )$ respectively do not coincide. The relation between the two is however understood and explained for example in [Reference Joyce and SongJS12, § 6.2] or [Reference Davison and MeinhardtDM15, § 6.7].
Both theories admit, at least in some specific geometries, refinements to motivic, cohomological and sheaf theoretic invariants. Let ![]() ${\mathbb {M}}_{\gamma }(X)$ denote some moduli stack of semi-stable sheaves on a smooth Calabi–Yau 3-fold; Joyce–Song theory is refined by the cohomology of a certain perverse sheaf
${\mathbb {M}}_{\gamma }(X)$ denote some moduli stack of semi-stable sheaves on a smooth Calabi–Yau 3-fold; Joyce–Song theory is refined by the cohomology of a certain perverse sheaf ![]() $\mathcal {D} T _{\gamma }$ on the moduli stack obtained (given an orientation data) gluing locally defined vanishing cycle sheaves (see [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Reference Brav, Bussi, Dupont, Joyce and SzendroiBBDJS15]). Kontsevich–Soibelman theory should instead be refined by the cohomology
$\mathcal {D} T _{\gamma }$ on the moduli stack obtained (given an orientation data) gluing locally defined vanishing cycle sheaves (see [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15, Reference Brav, Bussi, Dupont, Joyce and SzendroiBBDJS15]). Kontsevich–Soibelman theory should instead be refined by the cohomology ![]() $\text {H}^*(\operatorname {M}_{\gamma }(X),\Phi _{\gamma })$ for
$\text {H}^*(\operatorname {M}_{\gamma }(X),\Phi _{\gamma })$ for ![]() $\Phi _{\gamma }$ the so-called BPS sheaf, named after Bogomol’nyi, Prasad and Sommerfield, defined on the moduli space
$\Phi _{\gamma }$ the so-called BPS sheaf, named after Bogomol’nyi, Prasad and Sommerfield, defined on the moduli space ![]() $\operatorname {M}_{\gamma }(X)$ of S-equivalence classes. For
$\operatorname {M}_{\gamma }(X)$ of S-equivalence classes. For ![]() $X$ a compact CY3 threefold the existence of the sheaf
$X$ a compact CY3 threefold the existence of the sheaf ![]() $\Phi _{\gamma }$ is still conjectural; see [Reference TodaTod23] for a conjectural definition inspired to the case of moduli spaces of quiver representation with potential. In the latter situation, the BPS sheaf
$\Phi _{\gamma }$ is still conjectural; see [Reference TodaTod23] for a conjectural definition inspired to the case of moduli spaces of quiver representation with potential. In the latter situation, the BPS sheaf ![]() $\Phi _{\gamma }$, the sheaf on the moduli stack
$\Phi _{\gamma }$, the sheaf on the moduli stack ![]() $\mathcal {D} T _{\gamma }$ as well their relation are understood [Reference Davison and MeinhardtDM20].
$\mathcal {D} T _{\gamma }$ as well their relation are understood [Reference Davison and MeinhardtDM20].
Following [Reference Joyce and SongJS12] and [Reference Davison and MeinhardtDM20] in this paper we call the generalized DT invariants of Kontsevich and Soibelman BPS invariants, since as suggested by the authors themselves, their invariants should count BPS states.
Particularly interesting from the perspective of enumerative geometry is the case of one-dimensional sheaves on ![]() $X$, i.e. sheaves with Chern character
$X$, i.e. sheaves with Chern character ![]() $\gamma =(0,0,\beta,\chi )$. In this case the invariants arising from the moduli spaces of Gieseker semi-stable sheaves are (conjecturally) related to Gopakumar–Vafa invariants [Reference KatzKat08, Reference Maulik and TodaMT18, Reference TodaTod23].
$\gamma =(0,0,\beta,\chi )$. In this case the invariants arising from the moduli spaces of Gieseker semi-stable sheaves are (conjecturally) related to Gopakumar–Vafa invariants [Reference KatzKat08, Reference Maulik and TodaMT18, Reference TodaTod23].
Our main focus is the special case where the CY3-fold is a del Pezzo or a K3 local surface ![]() $X=\operatorname {Tot}(S)$. In these cases the BPS sheaf is better understood. For a local del Pezzo case a result of Meinhardt [Reference MeinhardtMei15] states that
$X=\operatorname {Tot}(S)$. In these cases the BPS sheaf is better understood. For a local del Pezzo case a result of Meinhardt [Reference MeinhardtMei15] states that ![]() $\Phi _{\beta,\chi }$ exists and coincides with the intersection complex
$\Phi _{\beta,\chi }$ exists and coincides with the intersection complex ![]() $IC_{\operatorname {M}_{\beta,\chi }}$ of the moduli space of S-equivalence classes. For a local K3 the situation is more complicated and an explicit description of the BPS sheaf has only recently been given in [Reference Davison, Hennecart and MejiaDHM23].
$IC_{\operatorname {M}_{\beta,\chi }}$ of the moduli space of S-equivalence classes. For a local K3 the situation is more complicated and an explicit description of the BPS sheaf has only recently been given in [Reference Davison, Hennecart and MejiaDHM23].
The main result of the present paper gives a surprising relation between the ![]() $\mathrm {BPS}$ invariants of local del Pezzo surfaces and certain non-archimedean (or
$\mathrm {BPS}$ invariants of local del Pezzo surfaces and certain non-archimedean (or ![]() $p$-adic) integrals. The relation is indirect and relies on results of Maulik and Shen [Reference Maulik and ShenMS23] which we explain next.
$p$-adic) integrals. The relation is indirect and relies on results of Maulik and Shen [Reference Maulik and ShenMS23] which we explain next.
1.1 Cohomological  $\chi$ independence and trace of Frobenius
$\chi$ independence and trace of Frobenius
Let ![]() $S$ be a smooth surface over
$S$ be a smooth surface over ![]() $\mathbb {C}$ and
$\mathbb {C}$ and ![]() $\beta$ an ample base point free class. We denote by
$\beta$ an ample base point free class. We denote by ![]() ${\mathbb {M}}_{\beta,\chi }(S)$ the moduli stack of Gieseker semi-stable (with respect to some fixed polarization
${\mathbb {M}}_{\beta,\chi }(S)$ the moduli stack of Gieseker semi-stable (with respect to some fixed polarization ![]() $H$) one-dimensional sheaves, and by
$H$) one-dimensional sheaves, and by ![]() $\operatorname {M}_{\beta,\chi }(S)$ the moduli space of S-equivalence classes. When
$\operatorname {M}_{\beta,\chi }(S)$ the moduli space of S-equivalence classes. When ![]() $S$ is del Pezzo, the stack of semi-stables is smooth. Under this hypothesis Maulik and Shen [Reference Maulik and ShenMS23] have recently proved the independence of the intersection cohomology from the Euler characteristic:Footnote 1
$S$ is del Pezzo, the stack of semi-stables is smooth. Under this hypothesis Maulik and Shen [Reference Maulik and ShenMS23] have recently proved the independence of the intersection cohomology from the Euler characteristic:Footnote 1
In fact, they prove a stronger statement, namely that the pushforward of the intersection complexes along the Hilbert–Chow morphisms ![]() $h_{\chi },h_{\chi '}$ are isomorphic. We denote by
$h_{\chi },h_{\chi '}$ are isomorphic. We denote by ![]() $h_\chi$ the morphism
$h_\chi$ the morphism
associating to a sheaf its Fitting support.
The result proves a refinement of a special case of a more general and long-standing conjecture in the enumerative geometry of smooth CY3-fold, known as the Pandharipande–Thomas strong rationality conjecture [Reference Pandharipande and ThomasPT10] and later reformulated by Toda [Reference TodaTod14] as the multiple cover formula conjecture for generalized DT invariants of moduli spaces of one dimensional sheaves. Translated in the Kontsevich–Soibelmain theory, the conjecture predicts the independence of the BPS invariants from the Euler characteristic.
The conjecture is expected to hold more in general at the refined level.
Now, choosing a spreading out, we can assume that the moduli spaces ![]() $\operatorname {M}_{\beta,\chi }(S)$ we are considering are defined over some large finite field
$\operatorname {M}_{\beta,\chi }(S)$ we are considering are defined over some large finite field ![]() $k=\mathbb {F}_q$ and that
$k=\mathbb {F}_q$ and that ![]() $\chi$ independence of
$\chi$ independence of ![]() $\Phi _{\beta,\chi }$ holds over
$\Phi _{\beta,\chi }$ holds over ![]() $k$ (see, for example, [Reference Beilinson, Bernstein, Deligne and GabberBBDG18, § 6] for precise definitions and results on spreading out of constructible complexes). We can then look at the function:
$k$ (see, for example, [Reference Beilinson, Bernstein, Deligne and GabberBBDG18, § 6] for precise definitions and results on spreading out of constructible complexes). We can then look at the function:
We call a pair ![]() $(\beta,\chi )$ generic (with respect to
$(\beta,\chi )$ generic (with respect to ![]() $H$), if any Gieseker semi-stable sheaf in
$H$), if any Gieseker semi-stable sheaf in ![]() ${\mathbb {M}}_{\beta,\chi }$ is stable. In this case
${\mathbb {M}}_{\beta,\chi }$ is stable. In this case ![]() ${\mathbb {M}}_{\beta,\chi } \to \operatorname {M}_{\beta,\chi }$ is a
${\mathbb {M}}_{\beta,\chi } \to \operatorname {M}_{\beta,\chi }$ is a ![]() ${\mathbb {G}}_m$ gerbe and, in particular,
${\mathbb {G}}_m$ gerbe and, in particular, ![]() $\operatorname {M}_{\beta,\chi }$ is smooth. Then the function
$\operatorname {M}_{\beta,\chi }$ is smooth. Then the function ![]() $\operatorname {BPS}_{\beta,\chi }$ will have the following two properties:
$\operatorname {BPS}_{\beta,\chi }$ will have the following two properties:
(i)
 $\mathrm {BPS}_{\beta,\chi }\equiv q^{-\dim \operatorname {M}_{\beta,\chi }}$ if
$\mathrm {BPS}_{\beta,\chi }\equiv q^{-\dim \operatorname {M}_{\beta,\chi }}$ if  $(\beta,\chi )$ is generic;
$(\beta,\chi )$ is generic;(ii) for all
 $\chi,\chi '\in \mathbb {Z}$ and for all
$\chi,\chi '\in \mathbb {Z}$ and for all  $y\in B(k)$ we have
$y\in B(k)$ we have
 \[ \sum _{x\in h_{\chi}^{-1}(y)(k)} \operatorname{BPS}_{\beta,\chi}(x)= \sum_{x\in h_{\chi'}^{-1}(y)(k)} \operatorname{BPS}_{\beta,\chi'}(x), \]
\[ \sum _{x\in h_{\chi}^{-1}(y)(k)} \operatorname{BPS}_{\beta,\chi}(x)= \sum_{x\in h_{\chi'}^{-1}(y)(k)} \operatorname{BPS}_{\beta,\chi'}(x), \]
the second being a consequence of [Reference Maulik and ShenMS23].
The main content of the paper is the construction of a function ![]() $p\mathrm {BPS}_{\beta,\chi }$ via non-archimedean integration satisfying these two properties.
$p\mathrm {BPS}_{\beta,\chi }$ via non-archimedean integration satisfying these two properties.
1.2 p-adic BPS function and its invariance
Consider ![]() $S$ a smooth del Pezzo surface over
$S$ a smooth del Pezzo surface over ![]() $\mathsf {Spec}({\mathcal {O}})$, where
$\mathsf {Spec}({\mathcal {O}})$, where ![]() ${\mathcal {O}}$ denotes the ring of integers of a non-archimedean local field
${\mathcal {O}}$ denotes the ring of integers of a non-archimedean local field ![]() $F$ with residue field
$F$ with residue field ![]() $k \cong {\mathbb {F}}_q$.
$k \cong {\mathbb {F}}_q$.
As recalled previously, the del Pezzo hypothesis ensures that the moduli stack is smooth, which allows us to construct in § 3 a canonical measure ![]() $\mu _{\rm can}$ on the
$\mu _{\rm can}$ on the ![]() $F$-analytic manifold
$F$-analytic manifold ![]() $\operatorname {M}_{\beta,\chi }(\mathcal {O})^\natural$ associated to
$\operatorname {M}_{\beta,\chi }(\mathcal {O})^\natural$ associated to ![]() $\operatorname {M}_{\beta,\chi }$.
$\operatorname {M}_{\beta,\chi }$.
In fact, the construction of ![]() $\mu _{\rm can}$ works more generally for normal, generically stabilizer-free, Artin stacks
$\mu _{\rm can}$ works more generally for normal, generically stabilizer-free, Artin stacks ![]() $\mathcal {M}$ admitting a universally closed morphism
$\mathcal {M}$ admitting a universally closed morphism ![]() $\mathcal {M}\xrightarrow {\pi }\operatorname {M}$ to a quasi-projective variety
$\mathcal {M}\xrightarrow {\pi }\operatorname {M}$ to a quasi-projective variety ![]() $\operatorname {M}$ such that
$\operatorname {M}$ such that ![]() $\pi$ is generically an isomorphism. The existence of a canonical measure in this context should be of independent interest.
$\pi$ is generically an isomorphism. The existence of a canonical measure in this context should be of independent interest.
Importantly, these hypothesis are also satisfied by moduli stacks ![]() $\operatorname {M}_{\beta,\chi }$ of semi-stable sheaves on
$\operatorname {M}_{\beta,\chi }$ of semi-stable sheaves on ![]() $S\to \mathsf {Spec}({\mathcal {O}})$ a smooth projective K3 over
$S\to \mathsf {Spec}({\mathcal {O}})$ a smooth projective K3 over ![]() ${\mathcal {O}}$ for many choices of
${\mathcal {O}}$ for many choices of ![]() $(\beta,\chi )$ (see § 3.2 for details), as well as by moduli stacks of (usual) Higgs bundles.
$(\beta,\chi )$ (see § 3.2 for details), as well as by moduli stacks of (usual) Higgs bundles.
Once defined the canonical measure on ![]() $\operatorname {M}_{\beta,\chi }(\mathcal {O})^\natural$, we then define the non-archimedean BPS function
$\operatorname {M}_{\beta,\chi }(\mathcal {O})^\natural$, we then define the non-archimedean BPS function ![]() $p\mathrm {BPS}_{\beta,\chi }$ as follows: for any
$p\mathrm {BPS}_{\beta,\chi }$ as follows: for any ![]() $x \in \operatorname {M}_{\beta,\chi }(k)$ denote by
$x \in \operatorname {M}_{\beta,\chi }(k)$ denote by ![]() $\operatorname {M}_{\beta,\chi }({\mathcal {O}})_x \subset M_{\beta,\chi }({\mathcal {O}})^\natural$ the ball of
$\operatorname {M}_{\beta,\chi }({\mathcal {O}})_x \subset M_{\beta,\chi }({\mathcal {O}})^\natural$ the ball of ![]() ${\mathcal {O}}$-rational points specializing to
${\mathcal {O}}$-rational points specializing to ![]() $x$ over
$x$ over ![]() $k$. Then
$k$. Then
is given by
where ![]() $\varphi _{\beta,\chi }$ is a certain complex-valued function associated with the natural
$\varphi _{\beta,\chi }$ is a certain complex-valued function associated with the natural ![]() ${\mathbb {G}}_m$ gerbe coming from the
${\mathbb {G}}_m$ gerbe coming from the ![]() ${\mathbb {G}}_m$-rigidification of
${\mathbb {G}}_m$-rigidification of ![]() ${\mathbb {M}}_{\beta,\chi }$ (see § 4 for the precise definition) and
${\mathbb {M}}_{\beta,\chi }$ (see § 4 for the precise definition) and ![]() $g$ is the arithmetic genus of the curves in the linear system
$g$ is the arithmetic genus of the curves in the linear system ![]() $|\beta |$.
$|\beta |$.
Our main result says that the non-archimedean BPS function enjoys the two properties above.
Theorem 1.2.2 (Theorem 5.0.2)
Let ![]() $S \to \mathsf {Spec}({\mathcal {O}})$ be either a smooth projective del Pezzo surface or a K3 surface satisfying Assumption 3.2.1. The function
$S \to \mathsf {Spec}({\mathcal {O}})$ be either a smooth projective del Pezzo surface or a K3 surface satisfying Assumption 3.2.1. The function ![]() $p\mathrm {BPS}_{\beta,\chi }: \operatorname {M}_{\beta,\chi }(k) \rightarrow {\mathbb {C}}$ satisfies the following two properties:
$p\mathrm {BPS}_{\beta,\chi }: \operatorname {M}_{\beta,\chi }(k) \rightarrow {\mathbb {C}}$ satisfies the following two properties:
(i)
 $p\mathrm {BPS}_{\beta,\chi } \equiv q^{-\dim \operatorname {M}_{\beta,\chi }}$ if
$p\mathrm {BPS}_{\beta,\chi } \equiv q^{-\dim \operatorname {M}_{\beta,\chi }}$ if  $(\beta,\chi )$ is generic;
$(\beta,\chi )$ is generic;(ii) for all
 $\chi,\chi '\in \mathbb {Z}$ and for all
$\chi,\chi '\in \mathbb {Z}$ and for all  $y\in B(k)$ we have
$y\in B(k)$ we have
 \[ \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\sum _{x\in h_{\chi'}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi'}(x). \]
\[ \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\sum _{x\in h_{\chi'}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi'}(x). \]
1.3 Relation to previous works, consequences and final considerations
The original motivation for Theorem 1.2.2 is a degree-independence result for Higgs bundles of rank coprime to the degree [Reference Groechenig, Wyss and ZieglerGWZ20b, Theorem 7.15], which in turn is a special case of a conjecture by Mozgovoy and Schiffmann [Reference Mozgovoy and SchiffmannMS14].Footnote 2 Thus, not surprisingly, the proof of Theorem 1.2.2 also relies on the same idea used in [Reference Groechenig, Wyss and ZieglerGWZ20b, Reference Groechenig, Wyss and ZieglerGWZ20a], which boils down to a Fubini argument along the Hilbert–Chow morphism ![]() $h_\chi$ and the fact that up to measure
$h_\chi$ and the fact that up to measure ![]() $0$, the fibers of
$0$, the fibers of ![]() $h_\chi$ over a non-archimedean local field are Picard schemes of smooth curves.
$h_\chi$ over a non-archimedean local field are Picard schemes of smooth curves.
As a corollary of Theorem 1.2.2, we obtain from [Reference Maulik and ShenMS23] (combined with the results in [Reference YuanYua23]) that after pushforward along ![]() $h_\chi$, the function
$h_\chi$, the function ![]() $p\mathrm {BPS}_{\beta,\chi }$ agrees with the trace of Frobenius on the
$p\mathrm {BPS}_{\beta,\chi }$ agrees with the trace of Frobenius on the ![]() $\mathrm {BPS}$ sheaf for the case of del Pezzo surfaces. The
$\mathrm {BPS}$ sheaf for the case of del Pezzo surfaces. The ![]() $\chi$-independence conjecture for
$\chi$-independence conjecture for ![]() $\mathrm {BPS}$ cohomology suggests, that this continues to hold in the K3 case.
$\mathrm {BPS}$ cohomology suggests, that this continues to hold in the K3 case.
A more concrete application of Theorem 1.2.2, via the Weil conjectures, is the ![]() $\chi$ independence of the Betti numbers for
$\chi$ independence of the Betti numbers for ![]() $\operatorname {M}_{\beta,\chi }$ as long as
$\operatorname {M}_{\beta,\chi }$ as long as ![]() $\chi$ and
$\chi$ and ![]() $\beta$ are coprime. For
$\beta$ are coprime. For ![]() $\mathbb {P}^2$ this is also a consequence of a more general result of Bousseau [Reference BousseauBou23, Conjecture 0.4.2, Theorem 0.4.5].
$\mathbb {P}^2$ this is also a consequence of a more general result of Bousseau [Reference BousseauBou23, Conjecture 0.4.2, Theorem 0.4.5].
When ![]() $\operatorname {M}_{\beta,\chi }$ is smooth, the first part of Theorem 1.2.2 implies
$\operatorname {M}_{\beta,\chi }$ is smooth, the first part of Theorem 1.2.2 implies
for all ![]() $x\in \operatorname {M}_{\beta,\chi }(k)$.
$x\in \operatorname {M}_{\beta,\chi }(k)$.
While for more general pairs ![]() $(\beta,\chi )$ Definition (1.2.1) has no obvious connection with the definition of the
$(\beta,\chi )$ Definition (1.2.1) has no obvious connection with the definition of the ![]() $\mathrm {BPS}$ function as trace of Frobenius of some suitable cohomology, Theorem 1.2.2 suggests that the above equality still holds.
$\mathrm {BPS}$ function as trace of Frobenius of some suitable cohomology, Theorem 1.2.2 suggests that the above equality still holds.
For the case of ![]() $S$ del Pezzo, this intriguing identity is the subject of an ongoing project of the third named author with Michael Groechenig and Paul Ziegler.
$S$ del Pezzo, this intriguing identity is the subject of an ongoing project of the third named author with Michael Groechenig and Paul Ziegler.
The refined ![]() $\chi$ independence for
$\chi$ independence for ![]() $\mathrm {BPS}$ invariants of moduli of sheaves on a K3 surface is instead still conjectural (see [Reference Maulik and ThomasMT19] for a proof of the numerical version), so is the identification of
$\mathrm {BPS}$ invariants of moduli of sheaves on a K3 surface is instead still conjectural (see [Reference Maulik and ThomasMT19] for a proof of the numerical version), so is the identification of ![]() $p\mathrm {BPS}$ and
$p\mathrm {BPS}$ and ![]() $\mathrm {BPS}$ invariants.
$\mathrm {BPS}$ invariants.
We expect that a conceptual proof (not relying on the ![]() $\chi$ independence) for the equality between
$\chi$ independence) for the equality between ![]() $p\mathrm {BPS}$ and
$p\mathrm {BPS}$ and ![]() $\mathrm {BPS}$ invariants will be easier to obtain in the Fano case, due to the smoothness of the moduli stacks.
$\mathrm {BPS}$ invariants will be easier to obtain in the Fano case, due to the smoothness of the moduli stacks.
Finally, as in [Reference Maulik and ShenMS23], we can prove the same statements for moduli of (meromorphic or not) Higgs bundles; that is, pairs of a vector bundle ![]() $\mathcal {E}$ on a curve
$\mathcal {E}$ on a curve ![]() $C$ of genus
$C$ of genus ![]() $g(C) \geq 2$ and a morphism
$g(C) \geq 2$ and a morphism ![]() $\Theta \colon \mathcal {E}\to \mathcal {E}(D)$ for
$\Theta \colon \mathcal {E}\to \mathcal {E}(D)$ for ![]() $D$ a fixed effective divisor of degree
$D$ a fixed effective divisor of degree ![]() $\deg (D)\geq 2g(C)-2$.
$\deg (D)\geq 2g(C)-2$.
In this case, the Hilbert–Chow morphism is replaced by the Hitchin fibration
 \[ H\colon \operatorname{M}_{r,\chi}(C)\to\bigoplus_{i=1}^r \operatorname{H}^0(C,\mathcal{O}_C(iD)) \]
\[ H\colon \operatorname{M}_{r,\chi}(C)\to\bigoplus_{i=1}^r \operatorname{H}^0(C,\mathcal{O}_C(iD)) \]
associating to ![]() $(\mathcal {E},\Theta )$ the characteristic polynomial of
$(\mathcal {E},\Theta )$ the characteristic polynomial of ![]() $\Theta$. The
$\Theta$. The ![]() $\chi$ independence for meromorphic Higgs bundles was also proven combinatorially in [Reference Mozgovoy and O'GormanMO19]. Moreover, during the writing of this article,
$\chi$ independence for meromorphic Higgs bundles was also proven combinatorially in [Reference Mozgovoy and O'GormanMO19]. Moreover, during the writing of this article, ![]() $\chi$ independence for
$\chi$ independence for ![]() $\mathrm {BPS}$ invariants of Higgs bundles has been proved in [Reference Kinjo and KosekiKK21]. This indirectly implies that our non-archimedean
$\mathrm {BPS}$ invariants of Higgs bundles has been proved in [Reference Kinjo and KosekiKK21]. This indirectly implies that our non-archimedean ![]() $p\mathrm {BPS}$ function agrees with the geometric
$p\mathrm {BPS}$ function agrees with the geometric ![]() $\mathrm {BPS}$ function beyond the Fano cases.
$\mathrm {BPS}$ function beyond the Fano cases.
This is in sharp contrast with the intersection complex on the coarse moduli space, which does depend on the Euler characteristic ![]() $\chi$ in the
$\chi$ in the ![]() $K3$ and Higgs bundle case, see [Reference Maulik and ShenMS23, § 0.4].
$K3$ and Higgs bundle case, see [Reference Maulik and ShenMS23, § 0.4].
2. Moduli spaces of sheaves and Higgs bundles
In this section we recall some properties of moduli spaces of sheaves on smooth surfaces and moduli spaces of (meromorphic or not) Higgs bundles relative to a base scheme ![]() $T.$
$T.$
The case ![]() $T=\mathsf {Spec}\, k$ with
$T=\mathsf {Spec}\, k$ with ![]() $k$ algebraically closed of
$k$ algebraically closed of ![]() $\operatorname {char}(k)=0$ is classical and all the statements can be found for example in [Reference Huybrechts and LehnHL97, § 4] for moduli of sheaves on surfaces, and in [Reference NitsureNit91] for moduli of Higgs bundles.
$\operatorname {char}(k)=0$ is classical and all the statements can be found for example in [Reference Huybrechts and LehnHL97, § 4] for moduli of sheaves on surfaces, and in [Reference NitsureNit91] for moduli of Higgs bundles.
For ![]() $T$ a field of positive or mixed characteristic, moduli spaces of sheaves were first constructed by Langer in [Reference LangerLan04b, Reference LangerLan04a]. More general moduli stacks and moduli spaces of sheaves and complexes over a smooth projective family
$T$ a field of positive or mixed characteristic, moduli spaces of sheaves were first constructed by Langer in [Reference LangerLan04b, Reference LangerLan04a]. More general moduli stacks and moduli spaces of sheaves and complexes over a smooth projective family ![]() $X/T$ were studied in [Reference LieblichLie06] and [Reference Huybrechts and ThomasHT10]. Recently the study of moduli stacks in the relative context has been vastly generalized in [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21].
$X/T$ were studied in [Reference LieblichLie06] and [Reference Huybrechts and ThomasHT10]. Recently the study of moduli stacks in the relative context has been vastly generalized in [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21].
We often cite the latter reference, even though the results of Langer, Lieblich and of Huybrechts–Thomas would suffice for our purposes.
2.1 Relative moduli spaces of sheaves on surfaces
Let ![]() $S\xrightarrow {r} T$ be a smooth family of projective surfaces, i.e.
$S\xrightarrow {r} T$ be a smooth family of projective surfaces, i.e. ![]() $r$ is smooth and projective. We are mostly interested in the case where the relative anti-canonical bundle
$r$ is smooth and projective. We are mostly interested in the case where the relative anti-canonical bundle ![]() $-K_{S/T}$ is
$-K_{S/T}$ is ![]() $r$-ample or trivial; we then say that
$r$-ample or trivial; we then say that ![]() $S$ is del Pezzo, respectively K3, over
$S$ is del Pezzo, respectively K3, over ![]() $T$.
$T$.
For us ![]() $T$ will be either
$T$ will be either ![]() $\mathsf {Spec} (\mathcal {O})$, or
$\mathsf {Spec} (\mathcal {O})$, or ![]() $\mathsf {Spec}\,F,$ or
$\mathsf {Spec}\,F,$ or ![]() $\mathsf {Spec}\,k$ where
$\mathsf {Spec}\,k$ where ![]() $F$ is a p-adic field,
$F$ is a p-adic field, ![]() $\mathcal {O}$ its ring of integers, and
$\mathcal {O}$ its ring of integers, and ![]() $k$ a field, possibly of positive characteristic.
$k$ a field, possibly of positive characteristic.
2.1.1 Construction of the moduli spaces
Let us fix ![]() $\beta$ on
$\beta$ on ![]() $S$ the class of an
$S$ the class of an ![]() $r$-effective divisor, ample and base point free, i.e.
$r$-effective divisor, ample and base point free, i.e. ![]() $\beta _{t}$ is ample and base point free for each
$\beta _{t}$ is ample and base point free for each ![]() $t \in T$. Given
$t \in T$. Given ![]() $\mathcal {F}$ a sheaf on
$\mathcal {F}$ a sheaf on ![]() $S$, flat over
$S$, flat over ![]() $T$, we say that
$T$, we say that ![]() $\mathcal {F}$ is one-dimensional over
$\mathcal {F}$ is one-dimensional over ![]() $T$ of class
$T$ of class ![]() $\beta$ if
$\beta$ if
with ![]() $C\in \mathbb {P}_T(g_*\mathcal {O}_S(\beta ))$. Since the Fitting support is compatible with pull-back [Sta, Tag 07Z6] this means that
$C\in \mathbb {P}_T(g_*\mathcal {O}_S(\beta ))$. Since the Fitting support is compatible with pull-back [Sta, Tag 07Z6] this means that ![]() $\mathcal {F}_{t}$ is supported on a curve of class
$\mathcal {F}_{t}$ is supported on a curve of class ![]() $\beta _{t}$ on
$\beta _{t}$ on ![]() $S_{t}$ for each
$S_{t}$ for each ![]() $t \in T$.
$t \in T$.
Let ![]() $\mathcal {O}_S(1)$ be a
$\mathcal {O}_S(1)$ be a ![]() $r$-polarization. Given
$r$-polarization. Given ![]() $\mathcal {F}$ a sheaf on
$\mathcal {F}$ a sheaf on ![]() $S$ flat over
$S$ flat over ![]() $T,$ the Hilbert polynomial
$T,$ the Hilbert polynomial
for ![]() $H_{t}\in |\mathcal {O}_{S_t}(1)|$ is locally constant on
$H_{t}\in |\mathcal {O}_{S_t}(1)|$ is locally constant on ![]() $T$ (see, for example, [Reference HartshorneHar77, Theorem 9.9]); in particular,
$T$ (see, for example, [Reference HartshorneHar77, Theorem 9.9]); in particular, ![]() $\chi (\mathcal {F}_{t})$ is locally constant.
$\chi (\mathcal {F}_{t})$ is locally constant.
We denote by ![]() $p_r(n)$ the reduced relative Hilbert polynomial obtained from
$p_r(n)$ the reduced relative Hilbert polynomial obtained from ![]() $P_r(n)$ dividing by the coefficient of the leading term.
$P_r(n)$ dividing by the coefficient of the leading term.
Definition 2.1.1 (see [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21, Definition 21.11])
Let ![]() $\beta,\chi$ and
$\beta,\chi$ and ![]() $\mathcal {O}_S(1)$ be as above. We denote by
$\mathcal {O}_S(1)$ be as above. We denote by
the functor whose value on ![]() $W\to T$ consist of sheaves
$W\to T$ consist of sheaves ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $S\times _T W,$ flat over
$S\times _T W,$ flat over ![]() $W$ such that for all
$W$ such that for all ![]() $w\in W$,
$w\in W$, ![]() $\mathcal {F}_w$ is a Gieseker semi-stable one-dimensional sheaf of class
$\mathcal {F}_w$ is a Gieseker semi-stable one-dimensional sheaf of class ![]() $\beta _w$ and Euler characteristic
$\beta _w$ and Euler characteristic ![]() $\chi \in \mathbb {Z}$. We recall that
$\chi \in \mathbb {Z}$. We recall that ![]() $\mathcal {F}_w$ is said Gieseker semi-stable if for all proper subsheaves
$\mathcal {F}_w$ is said Gieseker semi-stable if for all proper subsheaves ![]() $\mathcal {G}\in \mathcal {F}_w$ we have
$\mathcal {G}\in \mathcal {F}_w$ we have
and Gieseker stable if the inequality is strict. Finally, we say that ![]() $\mathcal {F}_w$ is geometrically Gieseker stable if its pull-back
$\mathcal {F}_w$ is geometrically Gieseker stable if its pull-back ![]() $\mathcal {F}_{\overline {w}}$ to the algebraic closure is Gieseker stable.
$\mathcal {F}_{\overline {w}}$ to the algebraic closure is Gieseker stable.
An object ![]() $\mathcal {F}\in \mathbb {M}_{\beta,\chi }(S)(W)$ is called a family of Gieseker semi-stable sheaves of class
$\mathcal {F}\in \mathbb {M}_{\beta,\chi }(S)(W)$ is called a family of Gieseker semi-stable sheaves of class ![]() $(\beta,\chi )$ over
$(\beta,\chi )$ over ![]() $W$.
$W$.
Here ![]() $\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ is the sub-functor of families of Gieseker geometrically stable objects.
$\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ is the sub-functor of families of Gieseker geometrically stable objects.
Theorem 2.1.3 [Reference LangerLan04b, Reference LangerLan04a, Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21]
In the notation above:
(i)
 $\mathbb {M}_{\beta,\chi }(S)$ and
$\mathbb {M}_{\beta,\chi }(S)$ and  $\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ are algebraic stacks of finite type over
$\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ are algebraic stacks of finite type over  $T$; the same statement hold for the
$T$; the same statement hold for the  $\mathbb {G}_m$-rigidification
$\mathbb {G}_m$-rigidification  $\mathcal {M}_{\beta,\chi }(S)$ of
$\mathcal {M}_{\beta,\chi }(S)$ of  $\mathbb {M}_{\beta,\chi }(S)$;
$\mathbb {M}_{\beta,\chi }(S)$;(ii) there exists a projective
 $T$-scheme
$T$-scheme  $\operatorname {M}_{\beta,\chi }(S)$ which uniformly represent the set valued functor over
$\operatorname {M}_{\beta,\chi }(S)$ which uniformly represent the set valued functor over  $T$-schemes associating to
$T$-schemes associating to  $W$ the set of
$W$ the set of  $\text {S}$-equivalence classes of families of Gieseker semi-stable sheaves on the fibers of
$\text {S}$-equivalence classes of families of Gieseker semi-stable sheaves on the fibers of  $S\times _T W\to W$ with Hilbert polynomial
$S\times _T W\to W$ with Hilbert polynomial  $p_r(n)$;
$p_r(n)$;(iii)
 $\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ is a
$\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ is a  $\mathbb {G}_m$ gerbe over its coarse moduli space
$\mathbb {G}_m$ gerbe over its coarse moduli space  $\operatorname {M}^{\rm st}_{\beta,\chi }(S)$, which is a quasi-projective scheme over
$\operatorname {M}^{\rm st}_{\beta,\chi }(S)$, which is a quasi-projective scheme over  $T$ representing isomorphism classes of Gieseker geometrically stable sheaves on the fibers of
$T$ representing isomorphism classes of Gieseker geometrically stable sheaves on the fibers of  $S\times _T W\to W$ with Hilbert polynomial
$S\times _T W\to W$ with Hilbert polynomial  $p_r(n)$;
$p_r(n)$;(iv)
 $\mathbb {M}_{\beta,\chi }(S)$ is universally closed over
$\mathbb {M}_{\beta,\chi }(S)$ is universally closed over  $T$ and, thus, universally closed over
$T$ and, thus, universally closed over  $\operatorname {M}_{\beta,\chi }(S)$.
$\operatorname {M}_{\beta,\chi }(S)$.
Proof. (i) A far more general version of this statement is proved in [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21, Theorem 21.24]. For the benefit of the reader, we recall the key steps of the proof in the special case of Langer [Reference LangerLan04a], which is the only one we need.
Let ![]() $E$ be a coherent sheaf on
$E$ be a coherent sheaf on ![]() $S$ flat on
$S$ flat on ![]() $T$, and let
$T$, and let ![]() $\operatorname {Quot}_{T,p_r(n)}(E)\colon (\operatorname {Sch}/T)^{{\rm op}}\rightarrow \operatorname {Sets}$ be the relative Quot functor, whose
$\operatorname {Quot}_{T,p_r(n)}(E)\colon (\operatorname {Sch}/T)^{{\rm op}}\rightarrow \operatorname {Sets}$ be the relative Quot functor, whose ![]() $W\to T$ valued points are quotients
$W\to T$ valued points are quotients ![]() $E_W\to Q\to 0$ with
$E_W\to Q\to 0$ with ![]() $Q$ a coherent sheaf on
$Q$ a coherent sheaf on ![]() $S\times _T W$, flat over
$S\times _T W$, flat over ![]() $W$, with Hilbert polynomial
$W$, with Hilbert polynomial ![]() $p_r(n)$ along the fibers of
$p_r(n)$ along the fibers of ![]() $S\times _T W\xrightarrow {r_W} W$. As proved for example in [Sta, Tag 09TQ],
$S\times _T W\xrightarrow {r_W} W$. As proved for example in [Sta, Tag 09TQ], ![]() $\operatorname {Quot}_{T,p_r(n)}(E)$ is represented by an algebraic space over
$\operatorname {Quot}_{T,p_r(n)}(E)$ is represented by an algebraic space over ![]() $T$ locally of finite presentation.
$T$ locally of finite presentation.
By Langer's results [Reference LangerLan04a, § 3], families of Gieseker semi-stable sheaves on the fibers of ![]() $S\xrightarrow {r} T$ with fixed Hilbert polynomial
$S\xrightarrow {r} T$ with fixed Hilbert polynomial ![]() $p_r(n)$ are bounded, i.e. any
$p_r(n)$ are bounded, i.e. any ![]() $\mathcal {F}\in \mathbb {M}_{\beta,\chi }(S)$ is a quotient of
$\mathcal {F}\in \mathbb {M}_{\beta,\chi }(S)$ is a quotient of ![]() $E=\mathcal {O}_S(-N)^{\oplus F(N)}$ for some fixed
$E=\mathcal {O}_S(-N)^{\oplus F(N)}$ for some fixed ![]() $N.$
$N.$
Furthermore, as shown in [Reference LangerLan04a, § 4], the open subsets ![]() $\mathcal {R}^{\rm st}\subseteq \mathcal {R}^{{\rm ss}}\subset \operatorname {Quot}_{T,p_r(n)}(E)$ of Gieseker stable/semi-stable sheaves on the fibers of
$\mathcal {R}^{\rm st}\subseteq \mathcal {R}^{{\rm ss}}\subset \operatorname {Quot}_{T,p_r(n)}(E)$ of Gieseker stable/semi-stable sheaves on the fibers of ![]() $S\xrightarrow {r} T$, correspond to the opens of stable/semi-stable points with respect to the natural action of the
$S\xrightarrow {r} T$, correspond to the opens of stable/semi-stable points with respect to the natural action of the ![]() $T$-smooth group
$T$-smooth group ![]() $\operatorname {GL}(F(N))$.
$\operatorname {GL}(F(N))$.
It thus follows that ![]() $\mathbb {M}_{\beta,\chi }(S)\cong [ \mathcal {R}^{{\rm ss}}/ \operatorname {GL}(F(N))]$ and
$\mathbb {M}_{\beta,\chi }(S)\cong [ \mathcal {R}^{{\rm ss}}/ \operatorname {GL}(F(N))]$ and ![]() $\mathbb {M}^{\rm st}_{\beta,\chi }(S)\cong [ \mathcal {R}^{\rm st}/ \operatorname {GL}(F(N))]$ as stacks over
$\mathbb {M}^{\rm st}_{\beta,\chi }(S)\cong [ \mathcal {R}^{\rm st}/ \operatorname {GL}(F(N))]$ as stacks over ![]() $\operatorname {Sch}/T$. The statement for the rigidification
$\operatorname {Sch}/T$. The statement for the rigidification ![]() $\mathcal {M}_{\beta,\chi }(S)$ now follows immediately as the latter is simply given by
$\mathcal {M}_{\beta,\chi }(S)$ now follows immediately as the latter is simply given by ![]() $[ \mathcal {R}^{{\rm ss}}/ \operatorname {PGL}(F(N))]$.
$[ \mathcal {R}^{{\rm ss}}/ \operatorname {PGL}(F(N))]$.
(ii) The projective ![]() $T$-scheme
$T$-scheme ![]() $\operatorname {M}_{\beta,\chi }(S)$ is the GIT quotient
$\operatorname {M}_{\beta,\chi }(S)$ is the GIT quotient ![]() $\mathcal {R}^{{\rm ss}}/ / \operatorname {GL}(F(N))$ this exists and has the claimed property by [Reference SeshadriSes77, Theorem 4], as also argued by Langer in the proof of [Reference LangerLan04a, Theorem 4.1].
$\mathcal {R}^{{\rm ss}}/ / \operatorname {GL}(F(N))$ this exists and has the claimed property by [Reference SeshadriSes77, Theorem 4], as also argued by Langer in the proof of [Reference LangerLan04a, Theorem 4.1].
(iii) The statement follows by the construction explained in statement (i).
(iv) The universal closedness over ![]() $T$ follows from a relative version of Langton's theorem. The reader can see [Reference LangtonLan75] or [Reference Huybrechts and LehnHL97, Theorem 2.B.1] for the proof over an algebraic closed field, and [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21, Lemma 21.22] for the general case.
$T$ follows from a relative version of Langton's theorem. The reader can see [Reference LangtonLan75] or [Reference Huybrechts and LehnHL97, Theorem 2.B.1] for the proof over an algebraic closed field, and [Reference Bayer, Lahoz, Macrì, Nuer, Perry and StellariBLM+21, Lemma 21.22] for the general case.
Given the GIT construction of the moduli space recalled above, the universal closedness of ![]() $\mathbb {M}_{\beta,\chi }(S)\to \operatorname {M}_{\beta,\chi }(S)$ also follows from [Reference Alper, Halpern-Leistner and HeinlothAHH23, Theorem A.8].
$\mathbb {M}_{\beta,\chi }(S)\to \operatorname {M}_{\beta,\chi }(S)$ also follows from [Reference Alper, Halpern-Leistner and HeinlothAHH23, Theorem A.8].
2.1.2 Deformation theory
Let ![]() $S\xrightarrow {r} T$ be as in the previous section, and let
$S\xrightarrow {r} T$ be as in the previous section, and let ![]() $\mathcal {F}$ be a coherent sheaf on
$\mathcal {F}$ be a coherent sheaf on ![]() $S$ flat over
$S$ flat over ![]() $T$. We denote by
$T$. We denote by ![]() $\operatorname {Ext}^i_S(\mathcal {F},\mathcal {F})$ the
$\operatorname {Ext}^i_S(\mathcal {F},\mathcal {F})$ the ![]() $T$ sheaf obtained by taking the
$T$ sheaf obtained by taking the ![]() $i$th cohomology of the complex
$i$th cohomology of the complex ![]() $Rr_*\operatorname {R}\mathcal {H}om(\mathcal {F},\mathcal {F}),$ i.e.
$Rr_*\operatorname {R}\mathcal {H}om(\mathcal {F},\mathcal {F}),$ i.e.
By [Reference LieblichLie06, § 3] (see also [Reference Huybrechts and ThomasHT10, § 4]) the sheaves ![]() $\operatorname {Ext}^i_S(\mathcal {F},\mathcal {F})$ control the deformation theory of
$\operatorname {Ext}^i_S(\mathcal {F},\mathcal {F})$ control the deformation theory of ![]() $\mathcal {F}$ over
$\mathcal {F}$ over ![]() $T$, namely:
$T$, namely:
(i) there is a natural isomorphism
 $\operatorname {Ext}^0_S(\mathcal {F},\mathcal {F})\cong \operatorname {End}(\mathcal {F},\mathcal {F})$;
$\operatorname {Ext}^0_S(\mathcal {F},\mathcal {F})\cong \operatorname {End}(\mathcal {F},\mathcal {F})$;(ii) the first-order deformations of
 $\mathcal {F}$ are given by
$\mathcal {F}$ are given by  $\operatorname {Ext}^1_S(\mathcal {F},\mathcal {F})$;
$\operatorname {Ext}^1_S(\mathcal {F},\mathcal {F})$;(iii) the obstruction to deformations are contained in
 $\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})$.
$\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})$.
Lemma 2.1.4 Let ![]() $S\xrightarrow {r} T$ be a smooth family of del Pezzo surfaces. Then
$S\xrightarrow {r} T$ be a smooth family of del Pezzo surfaces. Then ![]() ${\mathbb {M}}_{\beta,\chi }(S)$ is smooth over
${\mathbb {M}}_{\beta,\chi }(S)$ is smooth over ![]() $T$.
$T$.
Proof. It suffices to show that the obstruction ![]() $\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})$ is zero. We argue that
$\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})$ is zero. We argue that ![]() $\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})\otimes k(\bar {t})=0$ for any geometric point
$\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})\otimes k(\bar {t})=0$ for any geometric point ![]() $\bar {t}\in T$. By [Reference Altman and KleimanAK80, Theorem 1.9], the cohomology and base change property for Ext sheaves implies
$\bar {t}\in T$. By [Reference Altman and KleimanAK80, Theorem 1.9], the cohomology and base change property for Ext sheaves implies
where ![]() $\mathcal {F}_{\bar {t}}$ is, by definition, a Gieseker semi-stable sheaf of class
$\mathcal {F}_{\bar {t}}$ is, by definition, a Gieseker semi-stable sheaf of class ![]() $\beta _{\bar {t}}$ and Euler characteristic
$\beta _{\bar {t}}$ and Euler characteristic ![]() $\chi$ on
$\chi$ on ![]() $S_{\bar {t}}.$ The vanishing of the right-hand side is then classical; see, for example, [Reference Maulik and ShenMS23, Lemma 2.5].
$S_{\bar {t}}.$ The vanishing of the right-hand side is then classical; see, for example, [Reference Maulik and ShenMS23, Lemma 2.5].
2.1.3 Singularities in the K3 case
For ![]() $S\to T$ a K3 surface, it will never be the case that
$S\to T$ a K3 surface, it will never be the case that ![]() $\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})$ vanishes. Nonetheless, the following generalization of a classical result of Mukai [Reference MukaiMuk84] holds.
$\operatorname {Ext}^2_S(\mathcal {F},\mathcal {F})$ vanishes. Nonetheless, the following generalization of a classical result of Mukai [Reference MukaiMuk84] holds.
Theorem 2.1.5 [Reference InabaIna11, Theorem 3.2]
Let ![]() $S/ k$ be a smooth projective K3 surface over an algebraically closed field
$S/ k$ be a smooth projective K3 surface over an algebraically closed field ![]() $k$ and let
$k$ and let ![]() $\mathcal {F}$ be a simple sheaf, i.e.
$\mathcal {F}$ be a simple sheaf, i.e. ![]() $\operatorname {Hom}_{S}(\mathcal {F},\mathcal {F})=k$. Then the deformations of
$\operatorname {Hom}_{S}(\mathcal {F},\mathcal {F})=k$. Then the deformations of ![]() $\mathcal {F}$ are unobstructed. In particular, the open sub-stack
$\mathcal {F}$ are unobstructed. In particular, the open sub-stack ![]() $\operatorname {Spl}(S/ k)_{(\beta,\chi )}\subseteq \mathbb {M}_{\beta,\chi }(S)$ of simple semi-stable sheaves is smooth over
$\operatorname {Spl}(S/ k)_{(\beta,\chi )}\subseteq \mathbb {M}_{\beta,\chi }(S)$ of simple semi-stable sheaves is smooth over ![]() $k$.
$k$.
Corollary 2.1.6 Let ![]() $S \to T$ be a smooth projective relative K3 surface and
$S \to T$ be a smooth projective relative K3 surface and ![]() $T$ a smooth base with perfect residue fields. Then the moduli stack
$T$ a smooth base with perfect residue fields. Then the moduli stack ![]() $\operatorname {Spl}_{(\beta,\chi )}(S/ T)$ of simple semi-stable sheaves is smooth over
$\operatorname {Spl}_{(\beta,\chi )}(S/ T)$ of simple semi-stable sheaves is smooth over ![]() $T$.
$T$.
Proof. By Inaba's result, Theorem 2.1.5, the closed fibers of ![]() $\operatorname {Spl}_{(\beta,\chi )}(S/ T)\to T$ are smooth of dimension
$\operatorname {Spl}_{(\beta,\chi )}(S/ T)\to T$ are smooth of dimension ![]() $\beta _{\bar {t}}^2+2,$ and since
$\beta _{\bar {t}}^2+2,$ and since ![]() $S\to T$ is smooth this number is constant on
$S\to T$ is smooth this number is constant on ![]() $T$ (see [Reference FultonFul16, § 20.3]). It then follows from [Reference SchoutensSch10, Theorem 3.3.27] that
$T$ (see [Reference FultonFul16, § 20.3]). It then follows from [Reference SchoutensSch10, Theorem 3.3.27] that ![]() $\operatorname {Spl}_{(\beta,\chi )}(S/ T)\to T$ is flat and, thus, in fact smooth since all of the closed fibers are.
$\operatorname {Spl}_{(\beta,\chi )}(S/ T)\to T$ is flat and, thus, in fact smooth since all of the closed fibers are.
This immediately implies that ![]() $\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ is smooth for
$\mathbb {M}^{\rm st}_{\beta,\chi }(S)$ is smooth for ![]() $S \to T$ as in Corollary 2.1.6. Furthermore, for
$S \to T$ as in Corollary 2.1.6. Furthermore, for ![]() $T=\mathbb {C}$, the singularities of the moduli stack
$T=\mathbb {C}$, the singularities of the moduli stack ![]() $\mathbb {M}_{\beta,\chi }(S)$ have been studied intensively [Reference Arbarello and SaccàAS18, Reference Budur and ZhangBZ19, Reference DavisonDav23, Reference Crawley-BoeveyCra01]. In the following theorem, we state, in a form convenient for our purposes, some consequences of the results obtained in the quoted references.
$\mathbb {M}_{\beta,\chi }(S)$ have been studied intensively [Reference Arbarello and SaccàAS18, Reference Budur and ZhangBZ19, Reference DavisonDav23, Reference Crawley-BoeveyCra01]. In the following theorem, we state, in a form convenient for our purposes, some consequences of the results obtained in the quoted references.
Theorem 2.1.7 Let ![]() $S/ \mathbb {C}$ be a smooth projective K3 surface and
$S/ \mathbb {C}$ be a smooth projective K3 surface and ![]() $(\beta,\chi )$ a dimension vector such that the locus of
$(\beta,\chi )$ a dimension vector such that the locus of ![]() $\operatorname {Spl}_{\beta,\chi }^{{\rm ss}}(S)\subseteq \mathbb {M}_{\beta,\chi }(S)$ of simple semi-stable sheaves has complement of codimension at least two. Then
$\operatorname {Spl}_{\beta,\chi }^{{\rm ss}}(S)\subseteq \mathbb {M}_{\beta,\chi }(S)$ of simple semi-stable sheaves has complement of codimension at least two. Then ![]() $\mathbb {M}_{\beta,\chi }(S)$ is normal with local complete intersection singularities.
$\mathbb {M}_{\beta,\chi }(S)$ is normal with local complete intersection singularities.
Proof. For a morphism ![]() $Y\to X$ he property of being local complete intersection is étale local on source and target [Sta, Tag 06C3]. Thus, it is enough to argue that for any point
$Y\to X$ he property of being local complete intersection is étale local on source and target [Sta, Tag 06C3]. Thus, it is enough to argue that for any point ![]() $q\in \mathbb {M}_{\beta,\chi }(S)$ there exist an étale neighborhood
$q\in \mathbb {M}_{\beta,\chi }(S)$ there exist an étale neighborhood ![]() $U_q$ with local complete intersection singularities.
$U_q$ with local complete intersection singularities.
By [Reference DavisonDav23, Theorem 5.11], an étale local model for ![]() $\mathbb {M}_{\beta,\chi }(S)\to \text {M}_{\beta,\chi }(S)$ is given by the moduli stack
$\mathbb {M}_{\beta,\chi }(S)\to \text {M}_{\beta,\chi }(S)$ is given by the moduli stack ![]() $\mathfrak M_{\mathbf {d}}(\Pi _Q)=[\mu _{\mathbf {d}}^{-1}(0)/\operatorname {GL}_{\mathbf {d}}]$ (see [Reference DavisonDav23, § 3] for notation) of representations of the preprojective algebra of a certain explicit quiver, already considered in [Reference Arbarello and SaccàAS18].
$\mathfrak M_{\mathbf {d}}(\Pi _Q)=[\mu _{\mathbf {d}}^{-1}(0)/\operatorname {GL}_{\mathbf {d}}]$ (see [Reference DavisonDav23, § 3] for notation) of representations of the preprojective algebra of a certain explicit quiver, already considered in [Reference Arbarello and SaccàAS18].
On the other hand, by [Reference Crawley-BoeveyCra01, Theorem 1.2], ![]() $\mu _{\mathbf {d}}^{-1}(0)$ is a local complete intersection as soon as there exists a simple representation of the preprojective algebra with given dimension vector.
$\mu _{\mathbf {d}}^{-1}(0)$ is a local complete intersection as soon as there exists a simple representation of the preprojective algebra with given dimension vector.
By our assumptions, ![]() $\operatorname {Spl}_{\beta,\chi }^{{\rm ss}}(S)$ is dense in
$\operatorname {Spl}_{\beta,\chi }^{{\rm ss}}(S)$ is dense in ![]() $\mathbb {M}_{\beta,\chi }(S)$. This ensures the existence of a simple representation in
$\mathbb {M}_{\beta,\chi }(S)$. This ensures the existence of a simple representation in ![]() $U_q$ for each
$U_q$ for each ![]() $q$. Thus, since étale morphisms preserve the dimension of the automorphism groups and automorphism groups for quiver representations are connected, there exists a simple representation for
$q$. Thus, since étale morphisms preserve the dimension of the automorphism groups and automorphism groups for quiver representations are connected, there exists a simple representation for ![]() $\Pi _Q$ for each
$\Pi _Q$ for each ![]() $Q$ appearing in the local description.
$Q$ appearing in the local description.
Once we know that ![]() $\mathbb {M}_{\beta,\chi }(S)$ is local complete intersection, and thus Gorenstein, the normality simply follows from the assumption on the codimension of the locus of simple sheaves and Mukai and Inaba's Theorem 2.1.5.
$\mathbb {M}_{\beta,\chi }(S)$ is local complete intersection, and thus Gorenstein, the normality simply follows from the assumption on the codimension of the locus of simple sheaves and Mukai and Inaba's Theorem 2.1.5.
Remark 2.1.8 We show in § 2.2 that the hypothesis on the codimension of the complement of ![]() $\operatorname {Spl}_{\beta,\chi }^{{\rm ss}}(S)$ is satisfied as soon as:
$\operatorname {Spl}_{\beta,\chi }^{{\rm ss}}(S)$ is satisfied as soon as: ![]() $\beta$ is ample and base point free, and the locus
$\beta$ is ample and base point free, and the locus ![]() $V$ of non-reduced curves in the linear system
$V$ of non-reduced curves in the linear system ![]() $|\beta |$ is of codimension at least 2.
$|\beta |$ is of codimension at least 2.
For example, let ![]() $S$ be the K3 surface obtained as the 2:1 cover of
$S$ be the K3 surface obtained as the 2:1 cover of ![]() $S\xrightarrow {\tau }\mathbb {P}^2$ branched along a general sextic
$S\xrightarrow {\tau }\mathbb {P}^2$ branched along a general sextic ![]() $Z$. Consider
$Z$. Consider ![]() $\beta =\tau ^*[dL]$ for
$\beta =\tau ^*[dL]$ for ![]() $d\geq 1$. Then a curve
$d\geq 1$. Then a curve ![]() $C$ in
$C$ in ![]() $|\beta |$ is the 2:1 cover of a curve
$|\beta |$ is the 2:1 cover of a curve ![]() $D\in |dL|$ branched over
$D\in |dL|$ branched over ![]() $D\cap Z$. Then
$D\cap Z$. Then ![]() $C$ can be non-reduced only if, either
$C$ can be non-reduced only if, either ![]() $D$ itself is non-reduced or there is a component of
$D$ itself is non-reduced or there is a component of ![]() $D$ contained in
$D$ contained in ![]() $Z,$ i.e.
$Z,$ i.e. ![]() $Z$ is a component of
$Z$ is a component of ![]() $D$. Both loci have high codimension in
$D$. Both loci have high codimension in ![]() $|dL|$.
$|dL|$.
2.1.4 Hilbert–Chow map
We keep the notation of the previous section. Let us denote by ![]() $B_T=\mathbb {P}_T(g_*\mathcal {O}_S(\beta )),$ and by
$B_T=\mathbb {P}_T(g_*\mathcal {O}_S(\beta )),$ and by ![]() $\mathcal {C}\to B_T$ the universal curve. As for the case
$\mathcal {C}\to B_T$ the universal curve. As for the case ![]() $T=\mathsf {Spec}(\mathbb {C})$ there is a morphism
$T=\mathsf {Spec}(\mathbb {C})$ there is a morphism
which associate to ![]() $\mathcal {F}$ its fitting support and factors through the moduli space
$\mathcal {F}$ its fitting support and factors through the moduli space
We call ![]() $h_{\chi }$ the Hilbert–Chow morphism and
$h_{\chi }$ the Hilbert–Chow morphism and ![]() $\mathbf {h}_{\chi }$ the stacky Hilbert–Chow morphism. Since both
$\mathbf {h}_{\chi }$ the stacky Hilbert–Chow morphism. Since both ![]() $\operatorname {M}_{\beta,\chi }(S)$ and
$\operatorname {M}_{\beta,\chi }(S)$ and ![]() $B_T$ are projective over
$B_T$ are projective over ![]() $T,$
$T,$ ![]() $h_{\chi }$ is proper over
$h_{\chi }$ is proper over ![]() $T$.
$T$.
For ![]() $b\colon T\to B_T$ a section such that
$b\colon T\to B_T$ a section such that ![]() $\mathcal {C}_b/T$ is smooth, the fiber
$\mathcal {C}_b/T$ is smooth, the fiber ![]() $\mathbf {h}_{\chi }^{-1}(b)$ is the Picard stack
$\mathbf {h}_{\chi }^{-1}(b)$ is the Picard stack ![]() $\mathfrak {P}ic^{\chi +g-1}_{\mathcal {C}_b/T}$ where
$\mathfrak {P}ic^{\chi +g-1}_{\mathcal {C}_b/T}$ where ![]() $g$ is the genus of the curve, and
$g$ is the genus of the curve, and ![]() $h^{-1}_{\chi }(b)$ the Picard space
$h^{-1}_{\chi }(b)$ the Picard space ![]() $\operatorname {Pic}^{\chi +g-1}_{\mathcal {C}_b/T},$ i.e. the
$\operatorname {Pic}^{\chi +g-1}_{\mathcal {C}_b/T},$ i.e. the ![]() $\mathbb {G}_m$-rigidification.
$\mathbb {G}_m$-rigidification.
For ![]() $b\colon T\to B_T$, such that
$b\colon T\to B_T$, such that ![]() $\mathcal {C}_b/T$ is integral, the fiber of the stacky Hilbert–Chow morphism is some universally closed stack over
$\mathcal {C}_b/T$ is integral, the fiber of the stacky Hilbert–Chow morphism is some universally closed stack over ![]() $T$ containing
$T$ containing ![]() $\mathfrak {P}ic^{\chi +g-1}_{\mathcal {C}_b/T}$ as an open sub-stack, and
$\mathfrak {P}ic^{\chi +g-1}_{\mathcal {C}_b/T}$ as an open sub-stack, and ![]() $h^{-1}_{\chi }(b)$ is the corresponding GIT quotient, which is the compactification of the Picard space
$h^{-1}_{\chi }(b)$ is the corresponding GIT quotient, which is the compactification of the Picard space ![]() $\operatorname {Pic}^{\chi +g-1}_{\mathcal {C}_b/T}$ constructed by Altman and Kleiman [Reference Altman and KleimanAK80].
$\operatorname {Pic}^{\chi +g-1}_{\mathcal {C}_b/T}$ constructed by Altman and Kleiman [Reference Altman and KleimanAK80].
In general, for ![]() $\mathcal {C}_b/T$ non-integral not all line bundles of total degree
$\mathcal {C}_b/T$ non-integral not all line bundles of total degree ![]() $\operatorname {totdeg}=\chi +g-1$ are Gieseker semi-stable and one cannot say much about the fiber, except that it is a moduli stack of semi-stable sheaves of pure dimension 1. In the reduced case, moduli stacks and moduli spaces of rank-one semi-stable torsion free sheaves on
$\operatorname {totdeg}=\chi +g-1$ are Gieseker semi-stable and one cannot say much about the fiber, except that it is a moduli stack of semi-stable sheaves of pure dimension 1. In the reduced case, moduli stacks and moduli spaces of rank-one semi-stable torsion free sheaves on ![]() $\mathcal {C}_b/T$ have been studied, and in the following we recall some known results.
$\mathcal {C}_b/T$ have been studied, and in the following we recall some known results.
2.2 The open sub-stack of invertible sheaves
We denote by
the open sub-stack corresponding to line bundles of total degree ![]() $\chi +g-1$, which are Gieseker semi-stable on the fibers of
$\chi +g-1$, which are Gieseker semi-stable on the fibers of ![]() $\mathcal {C}/B_T$.
$\mathcal {C}/B_T$.
The rigidification ![]() $\mathcal {U}_{\beta,\chi }\subseteq \mathcal {M}_{\beta,\chi }(S)$ is stabilizer free, and
$\mathcal {U}_{\beta,\chi }\subseteq \mathcal {M}_{\beta,\chi }(S)$ is stabilizer free, and ![]() $\mathfrak {U}_{\beta,\chi }\to \mathcal {U}_{\beta,\chi }$ is simply a
$\mathfrak {U}_{\beta,\chi }\to \mathcal {U}_{\beta,\chi }$ is simply a ![]() $\mathbb {G}_m$ gerbe. It follows from Theorem 2.1.3, that if we further restrict to geometrically stable line bundles
$\mathbb {G}_m$ gerbe. It follows from Theorem 2.1.3, that if we further restrict to geometrically stable line bundles ![]() $\mathfrak {U}^{\rm st}_{\beta,\chi }$, the rigidification
$\mathfrak {U}^{\rm st}_{\beta,\chi }$, the rigidification ![]() $\mathcal {U}^{\rm st}_{\beta,\chi }$ is a good moduli space for the moduli stack and it is isomorphic to an open in
$\mathcal {U}^{\rm st}_{\beta,\chi }$ is a good moduli space for the moduli stack and it is isomorphic to an open in ![]() $\operatorname {M}_{\beta,\chi }(S)$.
$\operatorname {M}_{\beta,\chi }(S)$.
The opens ![]() $\mathcal {U}^{\rm st}_{\beta,\chi }\subseteq \mathcal {U}_{\beta,\chi }$ will play a crucial role in the construction of the canonical measure. To this end, we need to prove the following codimension estimate.
$\mathcal {U}^{\rm st}_{\beta,\chi }\subseteq \mathcal {U}_{\beta,\chi }$ will play a crucial role in the construction of the canonical measure. To this end, we need to prove the following codimension estimate.
Proposition 2.2.1
(i) Let
 $S\xrightarrow {r} T$ be a relative del Pezzo surface and
$S\xrightarrow {r} T$ be a relative del Pezzo surface and  $\beta$ a base point free and ample curve class. Then the complement of
$\beta$ a base point free and ample curve class. Then the complement of  $\,\mathcal {U}_{\beta,\chi }$ in
$\,\mathcal {U}_{\beta,\chi }$ in  $\mathcal {M}_{\beta,\chi }(S)$, or equivalently the complement of
$\mathcal {M}_{\beta,\chi }(S)$, or equivalently the complement of  $\mathfrak {U}_{\beta,\chi\!}$ in
$\mathfrak {U}_{\beta,\chi\!}$ in  ${\mathbb {M}}_{\beta,\chi }(S)$, has codimension at least two.
${\mathbb {M}}_{\beta,\chi }(S)$, has codimension at least two.(ii) Let
 $T=\operatorname {Spec}(\mathbb {C})$ and
$T=\operatorname {Spec}(\mathbb {C})$ and  $S$ a smooth projective K3 surface. Suppose furthermore that
$S$ a smooth projective K3 surface. Suppose furthermore that  $\beta$ is ample, base point free and the codimension of the non-reduced locus
$\beta$ is ample, base point free and the codimension of the non-reduced locus  $V\subset B$ is at least 2. Then the complement of
$V\subset B$ is at least 2. Then the complement of  $\mathcal {U}_{\beta,\chi }$ in
$\mathcal {U}_{\beta,\chi }$ in  $\mathcal {M}_{\beta,\chi }(S)$ has codimension at least two.
$\mathcal {M}_{\beta,\chi }(S)$ has codimension at least two.
The proof of this statement is somewhat involved and it will occupy the rest of the section. The reader who wish to get to the core of the paper quickly may skip this in a first reading.
Proof of Proposition 2.2.1 In case (i), by Lemma 2.1.4, ![]() ${\mathbb {M}}_{\beta,\chi }(S)\to T$ is smooth, so it is sufficient to estimate the codimension of the locus of line bundles on each geometric fiber
${\mathbb {M}}_{\beta,\chi }(S)\to T$ is smooth, so it is sufficient to estimate the codimension of the locus of line bundles on each geometric fiber ![]() ${\mathbb {M}}_{\beta _{\bar {t}},\chi }(S_{\bar {t}})\to \mathsf {Spec}(\bar {k})$. In case (ii) we are already by hypothesis working on an algebraically closed field. This allows us to reduce to the following classical setting.
${\mathbb {M}}_{\beta _{\bar {t}},\chi }(S_{\bar {t}})\to \mathsf {Spec}(\bar {k})$. In case (ii) we are already by hypothesis working on an algebraically closed field. This allows us to reduce to the following classical setting.
Setting 2.2.2 The surface ![]() $S$ is a smooth del Pezzo or K3 surface over
$S$ is a smooth del Pezzo or K3 surface over ![]() $\bar {k}$ an algebraically closed field;
$\bar {k}$ an algebraically closed field; ![]() $H$ is a polarization on
$H$ is a polarization on ![]() $S$,
$S$, ![]() $\beta$ is a base point free and ample curve class and
$\beta$ is a base point free and ample curve class and ![]() $B=|\beta |$ the linear system of curves in class
$B=|\beta |$ the linear system of curves in class ![]() $\beta.$
$\beta.$
Working on ![]() $T=\mathsf {Spec}(\bar {k})$ allows us to appeal to the results of [Reference Maulik and ShenMS23, Reference YuanYua23]. It is proved in [Reference YuanYua23], with techniques inspired by [Reference SchiffmannSch16], that for smooth projective surfaces
$T=\mathsf {Spec}(\bar {k})$ allows us to appeal to the results of [Reference Maulik and ShenMS23, Reference YuanYua23]. It is proved in [Reference YuanYua23], with techniques inspired by [Reference SchiffmannSch16], that for smooth projective surfaces ![]() $S$ over an algebraically closed field
$S$ over an algebraically closed field ![]() $\bar {k}$ with canonical
$\bar {k}$ with canonical ![]() $K_S\leq 0$ the stacky Hilbert–Chow morphism
$K_S\leq 0$ the stacky Hilbert–Chow morphism ![]() $\mathbf {h}_{\chi }$ (and, thus, also
$\mathbf {h}_{\chi }$ (and, thus, also ![]() $h_{\chi }$) is equidimensional.
$h_{\chi }$) is equidimensional.
Theorem 2.2.3 [Reference YuanYua23, Theorem 1.2, Corollary 1.3]
Let ![]() $S$ be a smooth projective surface and
$S$ be a smooth projective surface and ![]() $\beta =\sum _{i=1}^n m_i\beta _i$ an ample effective curve class with
$\beta =\sum _{i=1}^n m_i\beta _i$ an ample effective curve class with ![]() $\beta _i$ pairwise distinct. If
$\beta _i$ pairwise distinct. If ![]() $K_S\cdot \beta _i\leq 0$ for all
$K_S\cdot \beta _i\leq 0$ for all ![]() $i$, then
$i$, then
for any ![]() $b\in |\beta |$, where
$b\in |\beta |$, where ![]() $g=\frac {1}{2} \beta \cdot (\beta +K_S)+1$.
$g=\frac {1}{2} \beta \cdot (\beta +K_S)+1$.
Using the dimension estimate, Maulik and Shen proved the following.
Corollary 2.2.4 [Reference Maulik and ShenMS23, Theorem 2.3]
For ![]() $S$ del Pezzo, Hilbert–Chow morphisms
$S$ del Pezzo, Hilbert–Chow morphisms ![]() $\mathbf {h}_{\chi }$ and
$\mathbf {h}_{\chi }$ and ![]() $h_{\chi }$ are equidimensional. In particular,
$h_{\chi }$ are equidimensional. In particular, ![]() $\operatorname {M}_{\beta,\chi }(S)$ is irreducible.
$\operatorname {M}_{\beta,\chi }(S)$ is irreducible.
Corollary 2.2.5 For ![]() $S$ a K3 over an algebraically closed field, Hilbert–Chow morphisms
$S$ a K3 over an algebraically closed field, Hilbert–Chow morphisms ![]() $\mathbf {h}_{\chi }$ and
$\mathbf {h}_{\chi }$ and ![]() $h_{\chi }$ are equidimensional. In particular,
$h_{\chi }$ are equidimensional. In particular, ![]() $\operatorname {M}_{\beta,\chi }(S)$ is irreducible.
$\operatorname {M}_{\beta,\chi }(S)$ is irreducible.
Proof. This is a word-by-word repetition of the argument in [Reference Maulik and ShenMS23, Theorem 2.3] given the dimension estimate in Theorem 2.2.3.
Remark 2.2.6 The dimension estimate ![]() $\dim (\mathbf {h}^{-1}_{\chi }(b))\leq g-1$ had previously been proved in [Reference Maulik and ShenMS23, Proposition 2.6] under the additional hypothesis that
$\dim (\mathbf {h}^{-1}_{\chi }(b))\leq g-1$ had previously been proved in [Reference Maulik and ShenMS23, Proposition 2.6] under the additional hypothesis that ![]() $S$ is a toric del Pezzo, by reducing the estimate to curves with underlying support a union of possibly non-reduced toric divisors, for which the results of [Reference Chaudouard and LaumonCL16] apply.
$S$ is a toric del Pezzo, by reducing the estimate to curves with underlying support a union of possibly non-reduced toric divisors, for which the results of [Reference Chaudouard and LaumonCL16] apply.
We use the equidimensionality of the (stacky) Hilbert–Chow as follows. First, by Bertini's theorem, since ![]() $\beta$ is ample and base point free, there is a dense open
$\beta$ is ample and base point free, there is a dense open ![]() $B^{sm}\subset B$ such that for
$B^{sm}\subset B$ such that for ![]() $b\in B^{sm}$ the curve
$b\in B^{sm}$ the curve ![]() ${\mathcal {C}}_b$ is a non-singular, integral curve of genus
${\mathcal {C}}_b$ is a non-singular, integral curve of genus ![]() $g=\frac {1}{2} \beta \cdot (\beta +K_S)+1$. In this case,
$g=\frac {1}{2} \beta \cdot (\beta +K_S)+1$. In this case, ![]() $\mathbf {h}_{\chi }^{-1}(b)\cong \mathfrak Pic^{\chi +g-1}_{{\mathcal {C}}_b},$ which is simply a
$\mathbf {h}_{\chi }^{-1}(b)\cong \mathfrak Pic^{\chi +g-1}_{{\mathcal {C}}_b},$ which is simply a ![]() $\mathbb {G}_m$ gerbe over the degree
$\mathbb {G}_m$ gerbe over the degree ![]() $\chi +g-1$ component of the Picard group.
$\chi +g-1$ component of the Picard group.
In particular, ![]() $\mathbf {h}_{\chi }^{-1}(B^{sm})$ is contained in the open sub-stack of (stable) line bundles. Note, furthermore, that since the number of connected components is lower semi-continuous in a proper flat family (see, for example, [Reference Deligne and MumfordDM69, Theorem 4.17]) all the curves in the linear system are connected.
$\mathbf {h}_{\chi }^{-1}(B^{sm})$ is contained in the open sub-stack of (stable) line bundles. Note, furthermore, that since the number of connected components is lower semi-continuous in a proper flat family (see, for example, [Reference Deligne and MumfordDM69, Theorem 4.17]) all the curves in the linear system are connected.
To prove the codimension estimate, we now look at the fibers of the Hilbert–Chow morphism over the locus of singular curves.
The complement of ![]() $B^{sm}$ in
$B^{sm}$ in ![]() $B$ has codimension 1, and by equidimensionality of
$B$ has codimension 1, and by equidimensionality of ![]() $\mathbf {h}_{\chi }$ so does
$\mathbf {h}_{\chi }$ so does ![]() $\mathbf {h}^{-1}_{\chi }(B\setminus B^{sm})$.
$\mathbf {h}^{-1}_{\chi }(B\setminus B^{sm})$.
Let us denote by ![]() $V\subseteq B\setminus B^{sm}$ the locus of non-reduced curves. We prove in § 2.2.1 that this has always codimension at least 2 in
$V\subseteq B\setminus B^{sm}$ the locus of non-reduced curves. We prove in § 2.2.1 that this has always codimension at least 2 in ![]() $B$ for
$B$ for ![]() $S$ del Pezzo, provided
$S$ del Pezzo, provided ![]() $\beta$ is a base point free ample class. For
$\beta$ is a base point free ample class. For ![]() $S$ a K3, the codimension of
$S$ a K3, the codimension of ![]() $V$ is at least two by assumption; see Remark 2.1.8 for examples where the assumption is verified. Then
$V$ is at least two by assumption; see Remark 2.1.8 for examples where the assumption is verified. Then ![]() $\mathbf {h}^{-1}_{\chi }(V)$ has codimension at least two, and it can be discarded for the purposes of estimating the codimension of the complement of
$\mathbf {h}^{-1}_{\chi }(V)$ has codimension at least two, and it can be discarded for the purposes of estimating the codimension of the complement of ![]() $\mathfrak {U}_{\beta,\chi }$.
$\mathfrak {U}_{\beta,\chi }$.
Finally, we study the fibers over ![]() $(B\setminus B^{sm})\setminus V$ in § 2.2.2 and prove that the locus of line bundles in
$(B\setminus B^{sm})\setminus V$ in § 2.2.2 and prove that the locus of line bundles in ![]() $\mathbf {h}_{\chi }^{-1}(b)$ is dense for all
$\mathbf {h}_{\chi }^{-1}(b)$ is dense for all ![]() $b\in (B\setminus B^{sm})\setminus V$.
$b\in (B\setminus B^{sm})\setminus V$.
In conclusion, the complement of ![]() $\mathfrak {U}_{\beta,\chi }$ is contained in the union of
$\mathfrak {U}_{\beta,\chi }$ is contained in the union of ![]() $\mathbf {h}^{-1}_{\chi }(V)$ and a divisor
$\mathbf {h}^{-1}_{\chi }(V)$ and a divisor ![]() $\mathfrak {D}\subset \mathbf {h}^{-1}_{\chi }(B\setminus B^{sm})$. These have both codimension at least two, which allows us to conclude.
$\mathfrak {D}\subset \mathbf {h}^{-1}_{\chi }(B\setminus B^{sm})$. These have both codimension at least two, which allows us to conclude.
2.2.1 Excluding the non-reduced locus
Consider the stratification of ![]() $B$ given by
$B$ given by
where ![]() $\underline {\beta }=\{m_1\beta _1,\ldots,m_s\beta _s\}$ with
$\underline {\beta }=\{m_1\beta _1,\ldots,m_s\beta _s\}$ with ![]() $s\geq 1$,
$s\geq 1$, ![]() $m_i\geq 1$, and
$m_i\geq 1$, and ![]() $\beta _i$ are distinct curve classes such that there exists an integral curve in
$\beta _i$ are distinct curve classes such that there exists an integral curve in ![]() $|\beta _i|$ for each
$|\beta _i|$ for each ![]() $i$;
$i$; ![]() $B_{\underline {\beta }}$ is the locally closed strata in
$B_{\underline {\beta }}$ is the locally closed strata in ![]() $B$ of curves of type
$B$ of curves of type ![]() $\underline {\beta }$, i.e.
$\underline {\beta }$, i.e.
 \begin{align*} B_{\underline{\beta}}=\bigg\{C=\sum_i
m_i C_i\in |\beta|,\ C_i\in |\beta_i|\bigg\}, \end{align*}
\begin{align*} B_{\underline{\beta}}=\bigg\{C=\sum_i
m_i C_i\in |\beta|,\ C_i\in |\beta_i|\bigg\}, \end{align*}
with ![]() $C_i$ integral.
$C_i$ integral.
Let ![]() $Z$ be an irreducible component in
$Z$ be an irreducible component in ![]() $\overline {B}_{\underline {\beta }}$; we denote by
$\overline {B}_{\underline {\beta }}$; we denote by ![]() $\delta _Z$ the dimension of the affine part of the Jacobian of
$\delta _Z$ the dimension of the affine part of the Jacobian of ![]() $\mathcal {C}_b$ for
$\mathcal {C}_b$ for ![]() $b\in Z^{\circ }\subseteq \overline {B}_{\underline {\beta }}$ generic, i.e.
$b\in Z^{\circ }\subseteq \overline {B}_{\underline {\beta }}$ generic, i.e.
Lemma 2.2.7 Let ![]() $\beta$ be a base point free ample class on a smooth del Pezzo surface. The locus
$\beta$ be a base point free ample class on a smooth del Pezzo surface. The locus ![]() $V\subset B$ of non-reduced curves has codimension at least two.
$V\subset B$ of non-reduced curves has codimension at least two.
Proof. The locus ![]() $V$ of non-reduced curves is the union of closed strata
$V$ of non-reduced curves is the union of closed strata ![]() $\overline {B}_{\underline {\beta }}$ with
$\overline {B}_{\underline {\beta }}$ with ![]() $\underline {\beta }$ having at least one
$\underline {\beta }$ having at least one ![]() $m_i\geq 2$. We want to show that the codimension of any irreducible component
$m_i\geq 2$. We want to show that the codimension of any irreducible component ![]() $Z$ of such a stratum
$Z$ of such a stratum ![]() $\overline {B}_{\underline {\beta }}$ is at least two in
$\overline {B}_{\underline {\beta }}$ is at least two in ![]() $B$. The proof follows from the following inequality which is proved in [Reference Maulik and ShenMS23, Proposition 4.3]:
$B$. The proof follows from the following inequality which is proved in [Reference Maulik and ShenMS23, Proposition 4.3]:
 \begin{equation} \operatorname{codim}(Z)\geq -K_S\cdot \bigg(\sum_i(m_i-1)\beta_i\bigg)+\delta_Z\geq 1+\delta_Z, \end{equation}
\begin{equation} \operatorname{codim}(Z)\geq -K_S\cdot \bigg(\sum_i(m_i-1)\beta_i\bigg)+\delta_Z\geq 1+\delta_Z, \end{equation}
where the second inequality holds since ![]() $-K_S$ is ample,
$-K_S$ is ample, ![]() $m_i-1\geq 0$ for each
$m_i-1\geq 0$ for each ![]() $i$ and
$i$ and ![]() $m_i-1\geq 1$ for at least one
$m_i-1\geq 1$ for at least one ![]() $i$ and, thus,
$i$ and, thus,
 \[ -K_S\cdot \bigg(\sum_i(m_i-1)\beta_i\bigg)\geq 1; \]
\[ -K_S\cdot \bigg(\sum_i(m_i-1)\beta_i\bigg)\geq 1; \]
since ![]() $-K_S$ is ample, the equality can hold only if all but one
$-K_S$ is ample, the equality can hold only if all but one ![]() $m_i$ are equal to
$m_i$ are equal to ![]() $1$.
$1$.
If the latter inequality is strict, we are done; otherwise we can assume that ![]() $m_1=2$ and
$m_1=2$ and ![]() $m_i=1$ for any other
$m_i=1$ for any other ![]() $i$. Again, if
$i$. Again, if ![]() $\delta _Z\geq 1$ we are done.
$\delta _Z\geq 1$ we are done.
To complete the proof we only need to look the cases where ![]() $m_1=2$,
$m_1=2$, ![]() $m_i=1$ for any other
$m_i=1$ for any other ![]() $i$, and
$i$, and ![]() $\delta _Z=0$.
$\delta _Z=0$.
Let us denote by ![]() $C:=\mathcal {C}_b$ for
$C:=\mathcal {C}_b$ for ![]() $b\in B_{\{2\beta _1,\beta _2,\ldots,\beta _s\}}$ a generic point in this stratum, by
$b\in B_{\{2\beta _1,\beta _2,\ldots,\beta _s\}}$ a generic point in this stratum, by ![]() $C'\subseteq C$ the reduced subcurve, and by
$C'\subseteq C$ the reduced subcurve, and by ![]() $\beta '=\beta -\beta _1$ its class.
$\beta '=\beta -\beta _1$ its class.
We have two short exact sequences:
 \begin{align*} & 0\to \mathcal{O}_{C_1}(-\beta'\cdot\beta_1)\to \mathcal{O}_{C}\to\mathcal{O}_{C'}\to 0\\ & 0\to O_{C'}\to \oplus\bigoplus_{i=1}^s\mathcal{O}_{\widetilde{C}_i}\to \bigoplus_{p\in C^{\prime{\rm sing}}}
\mathcal{O}_p^{\delta(p)}\to 0. \end{align*}
\begin{align*} & 0\to \mathcal{O}_{C_1}(-\beta'\cdot\beta_1)\to \mathcal{O}_{C}\to\mathcal{O}_{C'}\to 0\\ & 0\to O_{C'}\to \oplus\bigoplus_{i=1}^s\mathcal{O}_{\widetilde{C}_i}\to \bigoplus_{p\in C^{\prime{\rm sing}}}
\mathcal{O}_p^{\delta(p)}\to 0. \end{align*}
The latter is simply the normalization sequence for ![]() $\widetilde {C'}=\sqcup _{i=1}^s\widetilde {C}_i\to C'$ (see [Reference LiuLiu06, § 7.5]). We denoted by
$\widetilde {C'}=\sqcup _{i=1}^s\widetilde {C}_i\to C'$ (see [Reference LiuLiu06, § 7.5]). We denoted by
the so-called delta invariant of the singularity.
By [Reference LiuLiu06, Lemma 5.11], there is a surjective morphism of abelian groups
with kernel an affine unipotent group of dimension ![]() $\operatorname {dim}\operatorname {H}^1(C_1,\mathcal {O}_{C_1}(-\beta '\cdot \beta _1))$. Moreover, by [Reference LiuLiu06, Theorem 5.19],
$\operatorname {dim}\operatorname {H}^1(C_1,\mathcal {O}_{C_1}(-\beta '\cdot \beta _1))$. Moreover, by [Reference LiuLiu06, Theorem 5.19], ![]() $\operatorname {Pic}^0(C)$ is an extension of
$\operatorname {Pic}^0(C)$ is an extension of ![]() $\times \operatorname {Pic}^0(\widetilde {C}_i)$ by an affine group of dimension
$\times \operatorname {Pic}^0(\widetilde {C}_i)$ by an affine group of dimension
 \begin{equation} \bigg(\sum_{p\in C^{\prime{\rm sing}}} \delta (p)\bigg) -s+1, \end{equation}
\begin{equation} \bigg(\sum_{p\in C^{\prime{\rm sing}}} \delta (p)\bigg) -s+1, \end{equation}and, thus,
 \[ \delta_Z= \bigg(\sum_{p\in C^{\prime{\rm sing}}}{\delta (p)}\bigg) -s+1+
\operatorname{dim}\operatorname{H}^1(C_1,\mathcal{O}_{C_1}(-\beta'\cdot\beta_1)). \]
\[ \delta_Z= \bigg(\sum_{p\in C^{\prime{\rm sing}}}{\delta (p)}\bigg) -s+1+
\operatorname{dim}\operatorname{H}^1(C_1,\mathcal{O}_{C_1}(-\beta'\cdot\beta_1)). \]
One can prove by induction on the number ![]() $s$ of irreducible components that
$s$ of irreducible components that ![]() $\sum _{p\in C^{\prime{\rm sing}}} \delta (p) -s+1\geq 0$ with equality holding only if the only singularities are nodes and
$\sum _{p\in C^{\prime{\rm sing}}} \delta (p) -s+1\geq 0$ with equality holding only if the only singularities are nodes and ![]() $C'$ is of compact type, namely its dual graph is a tree. For the induction step look at the partial normalization of
$C'$ is of compact type, namely its dual graph is a tree. For the induction step look at the partial normalization of ![]() $C'$ given by
$C'$ given by ![]() $R\sqcup \overline {C'\setminus R}$ for
$R\sqcup \overline {C'\setminus R}$ for ![]() $R$ an irreducible component.
$R$ an irreducible component.
Let us also analyze the degree of ![]() $\mathcal {O}_{C_1}(-\beta '\cdot \beta _1)$. We can write
$\mathcal {O}_{C_1}(-\beta '\cdot \beta _1)$. We can write ![]() $\beta '=\beta ''+\beta _1$ with
$\beta '=\beta ''+\beta _1$ with ![]() $\beta ''$ and effective curve class, and we can assume that
$\beta ''$ and effective curve class, and we can assume that ![]() $\beta ''\cdot \beta _1>0$ otherwise
$\beta ''\cdot \beta _1>0$ otherwise ![]() $C'$ is not connected and we can estimate
$C'$ is not connected and we can estimate ![]() $\delta _Z$ separately on each connected component. From
$\delta _Z$ separately on each connected component. From ![]() $0\leq g(\beta _1)=\frac {1}{2} K_S\cdot \beta _1+ \frac {1}{2} \beta ^2_1+1$ and the fact that
$0\leq g(\beta _1)=\frac {1}{2} K_S\cdot \beta _1+ \frac {1}{2} \beta ^2_1+1$ and the fact that ![]() $K_S$ is anti-ample, it follows that
$K_S$ is anti-ample, it follows that ![]() $\beta ^2_1\geq -1$. In particular,
$\beta ^2_1\geq -1$. In particular, ![]() $-\beta '\cdot \beta _1=- \beta ''\cdot \beta _1- \beta ^2_1\leq 0$ with equality holding only in the case
$-\beta '\cdot \beta _1=- \beta ''\cdot \beta _1- \beta ^2_1\leq 0$ with equality holding only in the case ![]() $\beta _1^2=-1$, and
$\beta _1^2=-1$, and ![]() $\beta ''\cdot \beta _1=1$. However, if the equality is verified, then
$\beta ''\cdot \beta _1=1$. However, if the equality is verified, then ![]() $\beta \cdot \beta _1 <0$, contradicting the ampleness of
$\beta \cdot \beta _1 <0$, contradicting the ampleness of ![]() $\beta$.
$\beta$.
We can thus assume that ![]() $\mathcal {O}_{C_1}(-\beta '\cdot \beta _1)$ has strictly negative degree
$\mathcal {O}_{C_1}(-\beta '\cdot \beta _1)$ has strictly negative degree ![]() $d.$ By Riemann–Roch,
$d.$ By Riemann–Roch,
which is always positive unless ![]() $g(C_1)=0$ and
$g(C_1)=0$ and ![]() $d=-1$. In particular, in this case we must have:
$d=-1$. In particular, in this case we must have: ![]() $\beta ''\cdot \beta _1=1$,
$\beta ''\cdot \beta _1=1$, ![]() $\beta _1^2=0$ and
$\beta _1^2=0$ and ![]() $K_S\cdot \beta _1=-2$. We can thus give a better estimate of the codimension of the component
$K_S\cdot \beta _1=-2$. We can thus give a better estimate of the codimension of the component ![]() $Z$ in
$Z$ in ![]() $B$ corresponding to such curves. By [Reference Maulik and ShenMS23, Lemma 2.1], given
$B$ corresponding to such curves. By [Reference Maulik and ShenMS23, Lemma 2.1], given ![]() $\gamma$ an effective curve class, the dimension of the linear system
$\gamma$ an effective curve class, the dimension of the linear system ![]() $|\gamma |$ is
$|\gamma |$ is ![]() $\frac {1}{2}\gamma \cdot (\gamma -K_S)$. Thus,
$\frac {1}{2}\gamma \cdot (\gamma -K_S)$. Thus, ![]() $\dim B=\frac {1}{2}\beta \cdot (\beta -K_S)$, whereas the dimension of
$\dim B=\frac {1}{2}\beta \cdot (\beta -K_S)$, whereas the dimension of ![]() $Z$ is
$Z$ is ![]() $\frac {1}{2}\beta '\cdot (\beta '-K_S)$. We compute
$\frac {1}{2}\beta '\cdot (\beta '-K_S)$. We compute
 \begin{align*} \operatorname{codim}(Z)&=\tfrac{1}{2}\beta\cdot(\beta-K_S)-\tfrac{1}{2}\beta'\cdot(\beta-K_S)\\ &=\tfrac{1}{2}[(\beta'+\beta_1)^2 -K_S\cdot\beta-\beta'^2+K_S\cdot\beta')\\ &=\tfrac{1}{2}[2\beta'\cdot\beta_1-K_S\cdot\beta_1]=2. \end{align*}
\begin{align*} \operatorname{codim}(Z)&=\tfrac{1}{2}\beta\cdot(\beta-K_S)-\tfrac{1}{2}\beta'\cdot(\beta-K_S)\\ &=\tfrac{1}{2}[(\beta'+\beta_1)^2 -K_S\cdot\beta-\beta'^2+K_S\cdot\beta')\\ &=\tfrac{1}{2}[2\beta'\cdot\beta_1-K_S\cdot\beta_1]=2. \end{align*}
The assumption in case (ii) and Lemma 2.2.7 in case (i) of Proposition 2.2.1 allows us to disregard completely the locus ![]() $V$ of non-reduced curve.
$V$ of non-reduced curve.
2.2.2 Reduced curves
If ![]() ${\mathcal {C}}_b$ is integral, then any rank-one torsion free sheaf
${\mathcal {C}}_b$ is integral, then any rank-one torsion free sheaf ![]() $\mathcal {F}$ is strictly stable, independently from the choice of polarization. This is easily seen noting that for any proper sub-sheaf
$\mathcal {F}$ is strictly stable, independently from the choice of polarization. This is easily seen noting that for any proper sub-sheaf ![]() $\mathcal {G}\hookrightarrow \mathcal {F}$, the cokernel is supported on a dimension
$\mathcal {G}\hookrightarrow \mathcal {F}$, the cokernel is supported on a dimension ![]() $0$ sub-scheme, which imply the strict inequality in (2.1.2). In particular,
$0$ sub-scheme, which imply the strict inequality in (2.1.2). In particular, ![]() $\mathbf {h}_{\chi }^{-1}(b)$ is a
$\mathbf {h}_{\chi }^{-1}(b)$ is a ![]() $\mathbb {G}_m$ gerbe over the compactification
$\mathbb {G}_m$ gerbe over the compactification ![]() $\overline {\mathrm {Pic}}^{\chi +g-1}_{{\mathcal {C}}_b}$of
$\overline {\mathrm {Pic}}^{\chi +g-1}_{{\mathcal {C}}_b}$of ![]() $\mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$ of Altman and Kleiman [Reference Altman and KleimanAK80]. It was proved in [Reference RegoReg80, Theorem A] that for an integral curve with only planar singularities
$\mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$ of Altman and Kleiman [Reference Altman and KleimanAK80]. It was proved in [Reference RegoReg80, Theorem A] that for an integral curve with only planar singularities ![]() $\overline {\mathrm {Pic}}^{\chi +g-1}_{{\mathcal {C}}_b}$ is irreducible and, thus, the open of line bundles is dense.
$\overline {\mathrm {Pic}}^{\chi +g-1}_{{\mathcal {C}}_b}$ is irreducible and, thus, the open of line bundles is dense.
We are left to study the fiber ![]() $\mathbf {h}^{-1}_\chi (b)$ for
$\mathbf {h}^{-1}_\chi (b)$ for ![]() $b \in |\beta |$ a reduced but possibly reducible curve.
$b \in |\beta |$ a reduced but possibly reducible curve.
Proposition 2.2.10 Let ![]() $C$ be a reduced curve with planar singularities and polarization
$C$ be a reduced curve with planar singularities and polarization ![]() $H_C$. Let
$H_C$. Let ![]() ${\mathbb {M}}_{\chi }(C)$ be the moduli stack of Gieseker semi-stable rank-one torsion free sheaves on
${\mathbb {M}}_{\chi }(C)$ be the moduli stack of Gieseker semi-stable rank-one torsion free sheaves on ![]() $C$. Then the open substack
$C$. Then the open substack ![]() $\mathfrak {U}_{\chi }$ of semi-stable invertible sheaves is dense in
$\mathfrak {U}_{\chi }$ of semi-stable invertible sheaves is dense in ![]() ${\mathbb {M}}_{\chi }(C)$.
${\mathbb {M}}_{\chi }(C)$.
Proof. To show that ![]() $\mathfrak {U}_{\chi }\subseteq {\mathbb {M}}_{\chi }(C)$ is dense, we need to show that any point
$\mathfrak {U}_{\chi }\subseteq {\mathbb {M}}_{\chi }(C)$ is dense, we need to show that any point ![]() $F$ in
$F$ in ![]() ${\mathbb {M}}_{\chi }(C)$ is the limit of a family of line bundles on
${\mathbb {M}}_{\chi }(C)$ is the limit of a family of line bundles on ![]() $C$ in a one-parameter family. This now follows from the deformation theory of rank-one sheaves on planar curves. Let
$C$ in a one-parameter family. This now follows from the deformation theory of rank-one sheaves on planar curves. Let ![]() $q_1,\ldots q_k$ be the points (necessarily) in the singular locus
$q_1,\ldots q_k$ be the points (necessarily) in the singular locus ![]() $C^{{\rm sing}}$ where
$C^{{\rm sing}}$ where ![]() $F$ fails to be a line bundle. We look at the forgetful morphism
$F$ fails to be a line bundle. We look at the forgetful morphism
where ![]() $F_{q_i}$ is the stalk of
$F_{q_i}$ is the stalk of ![]() $F$ at
$F$ at ![]() $q_i$. Since we are looking at curves with planar singularities, the forgetful morphism is smooth [Reference Fantechi, Goettsche and Van SratenFGV99]. Thus, it is sufficient to show that the generic element in each local deformation space
$q_i$. Since we are looking at curves with planar singularities, the forgetful morphism is smooth [Reference Fantechi, Goettsche and Van SratenFGV99]. Thus, it is sufficient to show that the generic element in each local deformation space ![]() $R_{F_{q_i}}$ corresponds to a invertible module. However, this follows from the analogous statement for compactified Jacobians of integral planar curves [Reference RegoReg80]. More explicitly: in order to describe
$R_{F_{q_i}}$ corresponds to a invertible module. However, this follows from the analogous statement for compactified Jacobians of integral planar curves [Reference RegoReg80]. More explicitly: in order to describe ![]() $R_{F_{q_i}}$, consider an integral curve
$R_{F_{q_i}}$, consider an integral curve ![]() $C_{q_i}$ with
$C_{q_i}$ with ![]() $q_i$ as unique singular point. By [Reference RegoReg80] the Picard is dense in the compactified Jacobian, which in particular implies that the generic point in
$q_i$ as unique singular point. By [Reference RegoReg80] the Picard is dense in the compactified Jacobian, which in particular implies that the generic point in ![]() $R_{F_{q_i}}$ parametrizes a line bundle.
$R_{F_{q_i}}$ parametrizes a line bundle.
This concludes the proof of Proposition 2.2.1.
Remark 2.2.11 When there are no strictly semi-stables, and thus ![]() ${\mathbb {M}}_{\chi }(C)$ is a
${\mathbb {M}}_{\chi }(C)$ is a ![]() $\mathbb {G}_m$ gerbe on
$\mathbb {G}_m$ gerbe on ![]() $h_{\chi }^{-1}(C)=\operatorname {M}_{\chi }(C)$, it is stated in [Reference Melo, Rapagnetta and VivianiMRV17, Corollary 2.20] or also in [Reference López-MartínLop05, Theorem 4.5] that stable line bundles are dense in the moduli space.
$h_{\chi }^{-1}(C)=\operatorname {M}_{\chi }(C)$, it is stated in [Reference Melo, Rapagnetta and VivianiMRV17, Corollary 2.20] or also in [Reference López-MartínLop05, Theorem 4.5] that stable line bundles are dense in the moduli space.
When there are strictly semi-stables (which is the most interesting case for us) the density statement at the level of moduli spaces ![]() $\operatorname {M}_{\chi }(C)$ is false; the description of the moduli space in [Reference López-MartínLop05, Theorem 4.5] explains this fact.
$\operatorname {M}_{\chi }(C)$ is false; the description of the moduli space in [Reference López-MartínLop05, Theorem 4.5] explains this fact.
2.3 Moduli of Higgs bundles
Let ![]() $C\to T$ be a smooth projective curve. As for the case of sheaves on surfaces, there is an adaptation of theory of moduli stack and moduli spaces of Higgs bundles relative to a base
$C\to T$ be a smooth projective curve. As for the case of sheaves on surfaces, there is an adaptation of theory of moduli stack and moduli spaces of Higgs bundles relative to a base ![]() $T$. The case where
$T$. The case where ![]() $T$ is a field of positive characteristic is already considered in [Reference NgôNgô06].
$T$ is a field of positive characteristic is already considered in [Reference NgôNgô06].
We refer to [Reference Groechenig, Wyss and ZieglerGWZ20b, § 7.1] and references therein for the adaptation of the classical theory to the case of smooth curves over ![]() $T=\mathsf {Spec} (O_F),\mathsf {Spec}(F)$.
$T=\mathsf {Spec} (O_F),\mathsf {Spec}(F)$.
We denote by ![]() ${\mathbb {M}}_{r,\chi }(C)$ and
${\mathbb {M}}_{r,\chi }(C)$ and ![]() $\operatorname {M}_{r,\chi }(C)$ the moduli stack and moduli space of semi-stable Higgs bundles
$\operatorname {M}_{r,\chi }(C)$ the moduli stack and moduli space of semi-stable Higgs bundles ![]() $(\mathcal {E}, \Theta \colon \mathcal {E}\to \mathcal {E}\otimes \mathcal {O}_C(D))$ of rank
$(\mathcal {E}, \Theta \colon \mathcal {E}\to \mathcal {E}\otimes \mathcal {O}_C(D))$ of rank ![]() $r$ and Euler characteristic
$r$ and Euler characteristic ![]() $\chi$ on the fibers of
$\chi$ on the fibers of ![]() $C\to T$. Here
$C\to T$. Here ![]() $D$ is a relative effective divisor of degree
$D$ is a relative effective divisor of degree ![]() $d=\text {deg}(D) \geq 2g-2$ on the fibers of
$d=\text {deg}(D) \geq 2g-2$ on the fibers of ![]() $C\to T$. If equality holds, we assume that
$C\to T$. If equality holds, we assume that ![]() $D$ is the canonical divisor and
$D$ is the canonical divisor and ![]() $g \geq 2$.
$g \geq 2$.
The stability is the (fiber-wise) Gieseker stability for sub-bundles preserved by the Higgs field, i.e. ![]() $(\mathcal {E},\Theta )$ is semi-stable if for any
$(\mathcal {E},\Theta )$ is semi-stable if for any ![]() $\mathcal {F}\subseteq \mathcal {E}$ such that
$\mathcal {F}\subseteq \mathcal {E}$ such that ![]() $\Theta \rvert _{\mathcal {F}}\colon \mathcal {F}\to \mathcal {F}\otimes \mathcal {O}_C(D)$
$\Theta \rvert _{\mathcal {F}}\colon \mathcal {F}\to \mathcal {F}\otimes \mathcal {O}_C(D)$
The Hitchin fibration is the morphism:
 \[ H\colon \operatorname{M}_{r,\chi}(C)\to B_T:=\bigoplus_{i=1}^r H^0(C,\mathcal{O}_C(id)) \]
\[ H\colon \operatorname{M}_{r,\chi}(C)\to B_T:=\bigoplus_{i=1}^r H^0(C,\mathcal{O}_C(id)) \]
associating to ![]() $(\mathcal {E},\Theta )$ the coefficients of its characteristic polynomial.
$(\mathcal {E},\Theta )$ the coefficients of its characteristic polynomial.
Via the spectral correspondence [Reference HitchinHit87], ![]() ${\mathbb {M}}_{r,\chi }(C)$ can be interpreted as a moduli stack of one-dimensional sheaves
${\mathbb {M}}_{r,\chi }(C)$ can be interpreted as a moduli stack of one-dimensional sheaves ![]() $\mathcal {F}$ on the non-compact surface
$\mathcal {F}$ on the non-compact surface
with ![]() $[\operatorname {Supp}(\mathcal {F})]=r[C]$. The hypothesis on the degree of
$[\operatorname {Supp}(\mathcal {F})]=r[C]$. The hypothesis on the degree of ![]() $D$ implies that
$D$ implies that ![]() $S_C$ is del Pezzo, which, in turn, guarantees the smoothness of the moduli stack
$S_C$ is del Pezzo, which, in turn, guarantees the smoothness of the moduli stack ![]() ${\mathbb {M}}_{r,\chi }(C)$ and its
${\mathbb {M}}_{r,\chi }(C)$ and its ![]() ${\mathbb {G}}_m$-rigidification
${\mathbb {G}}_m$-rigidification ![]() ${\mathcal {M}}_{r,\chi }(C)$ for each
${\mathcal {M}}_{r,\chi }(C)$ for each ![]() $(r,\chi )$ similar to Lemma 2.1.4.
$(r,\chi )$ similar to Lemma 2.1.4.
Moreover, via the correspondence we can identify the fibers of the Hitchin fibration ![]() $H$ with the Simpson compactified Jacobians of the spectral curve
$H$ with the Simpson compactified Jacobians of the spectral curve ![]() $C_{P(t)}\subseteq S_C$ cut out by the polynomial
$C_{P(t)}\subseteq S_C$ cut out by the polynomial ![]() $\text {det}(\pi ^*\Theta -t\text {Id})$.
$\text {det}(\pi ^*\Theta -t\text {Id})$.
In the following theorem we collect the analogous statements of Theorem 2.1.3 and Proposition 2.2.1 for the moduli stack of meromorphic Higgs bundles. Since the proof is essentially the same as in the previous section we do not repeat it here.
Theorem 2.3.1
(i) The moduli stack
 ${\mathbb {M}}_{r,\chi }(C)$ and its
${\mathbb {M}}_{r,\chi }(C)$ and its  $\mathbb {G}_m$-rigidification
$\mathbb {G}_m$-rigidification  ${\mathcal {M}}_{r,\chi }(C)$ are algebraic stacks of finite type over
${\mathcal {M}}_{r,\chi }(C)$ are algebraic stacks of finite type over  $T$.
$T$.(ii) If
 $\operatorname {deg}(D) >2g-2$, then
$\operatorname {deg}(D) >2g-2$, then  ${\mathbb {M}}_{r,\chi }(C)$ is smooth over
${\mathbb {M}}_{r,\chi }(C)$ is smooth over  $T$.
$T$.(iii) If
 $D=K_C$ and
$D=K_C$ and  $T=\operatorname {Spec}(\mathbb {C})$, then
$T=\operatorname {Spec}(\mathbb {C})$, then  ${\mathbb {M}}_{r,\chi }(C)$ is normal.
${\mathbb {M}}_{r,\chi }(C)$ is normal.(iv) There exists a quasi-projective
 $T$-scheme
$T$-scheme  $\operatorname {M}_{r,\chi }(C)$, proper over
$\operatorname {M}_{r,\chi }(C)$, proper over  $B_T$ which uniformly represent the moduli functor of S-equivalence classes of Higgs bundles.
$B_T$ which uniformly represent the moduli functor of S-equivalence classes of Higgs bundles.(v) We have that
 ${\mathbb {M}}^{st}_{r,\chi }(C)$ is a
${\mathbb {M}}^{st}_{r,\chi }(C)$ is a  ${\mathbb {G}}_m$ gerbe over the moduli space
${\mathbb {G}}_m$ gerbe over the moduli space  $\operatorname {M}^{st}_{r,\chi }(C)$
$\operatorname {M}^{st}_{r,\chi }(C)$(vi) We have that
 ${\mathbb {M}}^{st}_{r,\chi }(C)$ is universally closed over
${\mathbb {M}}^{st}_{r,\chi }(C)$ is universally closed over  $T$ and thus over
$T$ and thus over  $\operatorname {M}^{st}_{r,\chi }(C)$
$\operatorname {M}^{st}_{r,\chi }(C)$(vii) The open
 $\mathcal {U}_{r,\chi }\subseteq {\mathcal {M}}_{r,\chi }(C)$ of Higgs bundles whose associated spectral sheaf is a line bundle is dense and its complement has codimension at least two in
$\mathcal {U}_{r,\chi }\subseteq {\mathcal {M}}_{r,\chi }(C)$ of Higgs bundles whose associated spectral sheaf is a line bundle is dense and its complement has codimension at least two in  ${\mathcal {M}}_{r,\chi }(C)$.
${\mathcal {M}}_{r,\chi }(C)$.
Remark 2.3.2 In the case of Higgs bundle, no extra assumption is necessary to show normality of the moduli stack. We can understand that from at least two points of view: in the language of [Reference Davison, Hennecart and MejiaDHM22], the moduli stack of Higgs bundles satisfies the totally negative CY2 property [Reference Davison, Hennecart and MejiaDHM22, § 7]; under this additional property the normality follows from the results of [Reference VernetVer22].
Otherwise, we note that the locus ![]() $V$ corresponding to non-reduced spectral curves in the Hitchin base
$V$ corresponding to non-reduced spectral curves in the Hitchin base ![]() $V$ has always codimension at least two and, thus, as in Proposition 2.2.1, the locus of Higgs bundle whose corresponding spectral sheaf is a line bundle has codimension at least two in the stack, which allows us to argue as in Theorem 2.1.7.
$V$ has always codimension at least two and, thus, as in Proposition 2.2.1, the locus of Higgs bundle whose corresponding spectral sheaf is a line bundle has codimension at least two in the stack, which allows us to argue as in Theorem 2.1.7.
The estimate on the codimension on ![]() $V$ can be given by an explicit calculation:
$V$ can be given by an explicit calculation:
By Riemann–Roch the base ![]() $B$ of the Hitchin fibration has dimension
$B$ of the Hitchin fibration has dimension
where ![]() $r$ is the fixed rank and
$r$ is the fixed rank and ![]() $d=\text {deg}\mathcal {O}_C(D)\geq 2g-2$. The non-reduced locus is the (closure of) the strata
$d=\text {deg}\mathcal {O}_C(D)\geq 2g-2$. The non-reduced locus is the (closure of) the strata ![]() $V_{kr_1,r_2} \subseteq B$ whose points correspond to polynomials in
$V_{kr_1,r_2} \subseteq B$ whose points correspond to polynomials in ![]() $t$ admitting a factorization of the form
$t$ admitting a factorization of the form
Thus, the codimension of the non-reduced locus is the minimum of the codimension of the strata ![]() $V_{kr_1,r_2}$. Now, the dimension of the strata is
$V_{kr_1,r_2}$. Now, the dimension of the strata is
and it is easy to see by direct computation that
for ![]() $d\geq 2g-1$ and
$d\geq 2g-1$ and
for ![]() $d=2g-2$.
$d=2g-2$.
3.  $p$-adic integration
$p$-adic integration
Let ![]() $F$ be a non-archimedean local field
$F$ be a non-archimedean local field ![]() $F$ with ring of integers
$F$ with ring of integers ![]() ${\mathcal {O}}$ and residue field
${\mathcal {O}}$ and residue field ![]() $k \cong {\mathbb {F}}_q$. We consider the normalized Haar measure
$k \cong {\mathbb {F}}_q$. We consider the normalized Haar measure ![]() $\mu$ on the locally compact group
$\mu$ on the locally compact group ![]() $(F,+)$ so that
$(F,+)$ so that ![]() $\mu ({\mathcal {O}}) = 1$.
$\mu ({\mathcal {O}}) = 1$.
Since ![]() $F$ is a completely valued field there is a basic theory of differential geometry available. In particular, one can define analytic manifolds and differential forms as over the reals, see [Reference IgusaIgu00, Reference Chambert-Loir, Nicaise and SebagCNS18] for details. Given an
$F$ is a completely valued field there is a basic theory of differential geometry available. In particular, one can define analytic manifolds and differential forms as over the reals, see [Reference IgusaIgu00, Reference Chambert-Loir, Nicaise and SebagCNS18] for details. Given an ![]() $n$-dimensional analytic manifold
$n$-dimensional analytic manifold ![]() $M$ and a non-vanishing
$M$ and a non-vanishing ![]() $n$-form
$n$-form ![]() $\omega$ on
$\omega$ on ![]() $M$, one defines a Borel measure
$M$, one defines a Borel measure ![]() $\mu _\omega$ on
$\mu _\omega$ on ![]() $M$ by writing in a local chart
$M$ by writing in a local chart ![]() $U \subset F^n$ of
$U \subset F^n$ of ![]() $M$
$M$
and integrating ![]() $|f|$ against the Haar measure on
$|f|$ against the Haar measure on ![]() $F^n$.
$F^n$.
We are interested in analytic manifolds that arise from algebraic geometry. Concretely, given a smooth, separated and finite-type ![]() $F$-scheme, or more generally
$F$-scheme, or more generally ![]() $F$-algebraic space
$F$-algebraic space ![]() $X$, its set of
$X$, its set of ![]() $F$-points
$F$-points ![]() $X(F)$ carries naturally the structure of an analytic manifold by the inverse function theorem.
$X(F)$ carries naturally the structure of an analytic manifold by the inverse function theorem.
3.1 The measure on the moduli spaces
Let ![]() ${\mathcal {M}}$ be a normal algebraic stack with a finite-type morphism to
${\mathcal {M}}$ be a normal algebraic stack with a finite-type morphism to ![]() $\mathsf {Spec}({\mathcal {O}})$ of dimension
$\mathsf {Spec}({\mathcal {O}})$ of dimension ![]() $n$. We assume that there exists a (quasi-)projective variety
$n$. We assume that there exists a (quasi-)projective variety ![]() $\operatorname {M}$ and a morphism
$\operatorname {M}$ and a morphism ![]() $\pi :{\mathcal {M}} \rightarrow M$ satisfying the following conditions: there exists a dense open substack
$\pi :{\mathcal {M}} \rightarrow M$ satisfying the following conditions: there exists a dense open substack ![]() $U' \subset {\mathcal {M}}$, smooth over
$U' \subset {\mathcal {M}}$, smooth over ![]() ${\mathcal {O}}$, that is stabilizer free, i.e. an algebraic space, and that the complement of
${\mathcal {O}}$, that is stabilizer free, i.e. an algebraic space, and that the complement of ![]() $U'$ has codimension at least
$U'$ has codimension at least ![]() $2$ in
$2$ in ![]() ${\mathcal {M}}$; there exists a second dense open
${\mathcal {M}}$; there exists a second dense open ![]() $U \subset U'$ such that
$U \subset U'$ such that ![]() $\pi$ restricted to
$\pi$ restricted to ![]() $U$ induces an isomorphism onto its image in
$U$ induces an isomorphism onto its image in ![]() $M$ which we also denote by
$M$ which we also denote by ![]() $U$.
$U$.
The goal of this section is to construct a canonical measure on the analytic manifold
For this we need the following extra assumption.
Assumption 3.1.1 For any ![]() $x \in M^\natural = M({\mathcal {O}}) \cap U(F)$ there exists a finite extension
$x \in M^\natural = M({\mathcal {O}}) \cap U(F)$ there exists a finite extension ![]() $L/F$ with ring of integers
$L/F$ with ring of integers ![]() ${\mathcal {O}}_L$ such that the base change
${\mathcal {O}}_L$ such that the base change ![]() $x_L:\mathsf {Spec}({\mathcal {O}}_L) \to M_L = M \times _{{\mathcal {O}}} {\mathcal {O}}_L$ admits a lift
$x_L:\mathsf {Spec}({\mathcal {O}}_L) \to M_L = M \times _{{\mathcal {O}}} {\mathcal {O}}_L$ admits a lift ![]() $x'_L:\mathsf {Spec}({\mathcal {O}}_L) \to {\mathcal {M}}_L$.
$x'_L:\mathsf {Spec}({\mathcal {O}}_L) \to {\mathcal {M}}_L$.
Note that Assumption 3.1.1 is, in particular, satisfied if ![]() ${\mathcal {M}} \to M$ is universally closed [Sta, 01KA].
${\mathcal {M}} \to M$ is universally closed [Sta, 01KA].
We fix a Zariski-open cover ![]() $U'= \bigcup _{i\in I} U'_i$ such that on each
$U'= \bigcup _{i\in I} U'_i$ such that on each ![]() $U'_i$ the relative canonical bundle
$U'_i$ the relative canonical bundle ![]() $\Omega _{U'/{\mathcal {O}}}^{n}$ is trivial and pick a trivializing (i.e. non-vanishing)
$\Omega _{U'/{\mathcal {O}}}^{n}$ is trivial and pick a trivializing (i.e. non-vanishing) ![]() $n$-form
$n$-form ![]() $\omega _i$ on
$\omega _i$ on ![]() $U'_i$. Let
$U'_i$. Let ![]() $U_i = U \cap U'_i$. We have a decomposition
$U_i = U \cap U'_i$. We have a decomposition
with ![]() $M_i^\natural = M({\mathcal {O}}) \cap U_i(F)$ and we claim that the measures
$M_i^\natural = M({\mathcal {O}}) \cap U_i(F)$ and we claim that the measures ![]() $\mu _{\omega _i}$ on
$\mu _{\omega _i}$ on ![]() $M_i^\natural$ glue to a measure on
$M_i^\natural$ glue to a measure on ![]() $M^\natural$ that is independent of the choice of
$M^\natural$ that is independent of the choice of ![]() $(\omega _i)_i$.
$(\omega _i)_i$.
Proposition 3.1.2 (The canonical measure on  $M^\natural$)
$M^\natural$)
For all ![]() $i,j \in I$ and any measurable subset
$i,j \in I$ and any measurable subset ![]() $A \subset M_i^\natural \cap M_j^\natural$ we have
$A \subset M_i^\natural \cap M_j^\natural$ we have
In particular, the family ![]() $(\mu _{\omega _i})_{i\in I}$ glues to a Borel measure
$(\mu _{\omega _i})_{i\in I}$ glues to a Borel measure ![]() $\mu _{{\rm can},{\mathcal {M}}}$ on
$\mu _{{\rm can},{\mathcal {M}}}$ on ![]() $M^\natural$. Furthermore,
$M^\natural$. Furthermore, ![]() $\mu _{{\rm can},{\mathcal {M}}}$ is independent of the choice of
$\mu _{{\rm can},{\mathcal {M}}}$ is independent of the choice of ![]() $(\omega _i)_{i\in I}$.
$(\omega _i)_{i\in I}$.
Proof. Since ![]() $\omega _i$ and
$\omega _i$ and ![]() $\omega _j$ are both non-vanishing sections of the same invertible sheaf over
$\omega _j$ are both non-vanishing sections of the same invertible sheaf over ![]() $U'$ we have
$U'$ we have ![]() $\omega _{j|U'_i \cap U'_j} = f \cdot \omega _{i|U'_i \cap U'_j}$ with
$\omega _{j|U'_i \cap U'_j} = f \cdot \omega _{i|U'_i \cap U'_j}$ with ![]() $f \in H^0(U'_i\cap U'_j, {\mathcal {O}}^*_{U'_i \cap U'_j})$. We claim that for every
$f \in H^0(U'_i\cap U'_j, {\mathcal {O}}^*_{U'_i \cap U'_j})$. We claim that for every ![]() $x \in M_i^\natural \cap M_j^\natural \subset (U_i \cap U_j)(F)$ we have that
$x \in M_i^\natural \cap M_j^\natural \subset (U_i \cap U_j)(F)$ we have that ![]() $f(x) \in {\mathcal {O}}_F^*$. This implies the first part of the proposition, since
$f(x) \in {\mathcal {O}}_F^*$. This implies the first part of the proposition, since ![]() $\mu _{\omega _i}$ and
$\mu _{\omega _i}$ and ![]() $\mu _{\omega _j}$ are given by locally integrating the absolute value of
$\mu _{\omega _j}$ are given by locally integrating the absolute value of ![]() $\omega _i$ and
$\omega _i$ and ![]() $\omega _j$.
$\omega _j$.
To prove the claim, let ![]() $L/F$ be a finite extension such that
$L/F$ be a finite extension such that ![]() $x_L$ lifts to an
$x_L$ lifts to an ![]() ${\mathcal {O}}_L$-point
${\mathcal {O}}_L$-point ![]() $x'_L$ of
$x'_L$ of ![]() ${\mathcal {M}}_L$ as in Assumption 3.1.1. Let
${\mathcal {M}}_L$ as in Assumption 3.1.1. Let ![]() $p: X \to {\mathcal {M}}$ be a smooth atlas. By passing to an even bigger finite extension of
$p: X \to {\mathcal {M}}$ be a smooth atlas. By passing to an even bigger finite extension of ![]() $F$ if necessary, we may further assume that the closed point
$F$ if necessary, we may further assume that the closed point ![]() $\mathsf {Spec}(k_L) \to {\mathcal {M}}_{k_L}$ lifts to the atlas
$\mathsf {Spec}(k_L) \to {\mathcal {M}}_{k_L}$ lifts to the atlas ![]() $X_{k_L}$. Since
$X_{k_L}$. Since ![]() $X_L \to {\mathcal {M}}_L$ is smooth we can then lift the whole
$X_L \to {\mathcal {M}}_L$ is smooth we can then lift the whole ![]() $x'_L$ to a morphism
$x'_L$ to a morphism ![]() $\tilde {x}_L: \mathsf {Spec}({\mathcal {O}}_L) \to X_L$ by Hensel's lemma. Since
$\tilde {x}_L: \mathsf {Spec}({\mathcal {O}}_L) \to X_L$ by Hensel's lemma. Since ![]() $F^* \cap {\mathcal {O}}_L = {\mathcal {O}}^*$ it is enough to show that
$F^* \cap {\mathcal {O}}_L = {\mathcal {O}}^*$ it is enough to show that ![]() $f(x_L) = f \circ \pi \circ p (\tilde {x}_L) \in {\mathcal {O}}_L^*$.
$f(x_L) = f \circ \pi \circ p (\tilde {x}_L) \in {\mathcal {O}}_L^*$.
Write ![]() $V_i = p^{-1}(U'_i)$. The point is now that
$V_i = p^{-1}(U'_i)$. The point is now that ![]() $f \circ p_{|V_i \cap V_j}$ is a regular non-vanishing function on
$f \circ p_{|V_i \cap V_j}$ is a regular non-vanishing function on ![]() $V_i \cap V_j$ and the complement of
$V_i \cap V_j$ and the complement of ![]() $V_i\cap V_j$ in
$V_i\cap V_j$ in ![]() $X$ has codimension at least
$X$ has codimension at least ![]() $2$ by assumption. Since
$2$ by assumption. Since ![]() $X$ is normal, Hartogs’ theorem applies and
$X$ is normal, Hartogs’ theorem applies and ![]() $f$ thus extends to a regular function on
$f$ thus extends to a regular function on ![]() $X$ which is still non-vanishing, as the
$X$ which is still non-vanishing, as the ![]() $0$-locus would have codimension
$0$-locus would have codimension ![]() $1$. Therefore,
$1$. Therefore,
as claimed.
The proof of the independence of ![]() $\mu _{{\rm can},{\mathcal {M}}}$ from
$\mu _{{\rm can},{\mathcal {M}}}$ from ![]() $(\omega _i)_{i\in I}$ is essentially the same.
$(\omega _i)_{i\in I}$ is essentially the same.
If the stack ![]() ${\mathcal {M}}$ is clear from the context we often write
${\mathcal {M}}$ is clear from the context we often write ![]() $\mu _{\rm can}$ instead of
$\mu _{\rm can}$ instead of ![]() $\mu _{{\rm can},{\mathcal {M}}}$.
$\mu _{{\rm can},{\mathcal {M}}}$.
Example 3.1.3 Consider the quotient stack ![]() ${\mathcal {M}} = [{\mathbb {A}}^2/{\mathbb {G}}_m]$ where
${\mathcal {M}} = [{\mathbb {A}}^2/{\mathbb {G}}_m]$ where ![]() ${\mathbb {G}}_m$ acts linearly on
${\mathbb {G}}_m$ acts linearly on ![]() ${\mathbb {A}}^2$ with weights
${\mathbb {A}}^2$ with weights ![]() $(1,-1)$. In the above notation we have
$(1,-1)$. In the above notation we have
Then ![]() $U'$ is isomorphic to the affine line with doubled origin, which admits an open cover by two copies of
$U'$ is isomorphic to the affine line with doubled origin, which admits an open cover by two copies of ![]() ${\mathbb {A}}^1$. The standard
${\mathbb {A}}^1$. The standard ![]() $1$-forms on these
$1$-forms on these ![]() ${\mathbb {A}}^1$ glue to a global non-vanishing
${\mathbb {A}}^1$ glue to a global non-vanishing ![]() $1$-form on
$1$-form on ![]() $U'$ and
$U'$ and ![]() $\mu _{\rm can}$ is given by integrating
$\mu _{\rm can}$ is given by integrating ![]() ${{\rm d}x}$ (i.e. the standard Haar measure) on
${{\rm d}x}$ (i.e. the standard Haar measure) on ![]() $M^\natural = {\mathcal {O}} \cap F^* = {\mathcal {O}} \setminus \{0\}$.
$M^\natural = {\mathcal {O}} \cap F^* = {\mathcal {O}} \setminus \{0\}$.
Remark 3.1.4 If ![]() ${\mathcal {M}} = M$ is stabilizer-free we have
${\mathcal {M}} = M$ is stabilizer-free we have ![]() $M^\natural = M({\mathcal {O}})$ and the construction of
$M^\natural = M({\mathcal {O}})$ and the construction of ![]() $\mu _{\rm can}$ goes back to Weil [Reference WeilWei12]. The volume is related to the number of
$\mu _{\rm can}$ goes back to Weil [Reference WeilWei12]. The volume is related to the number of ![]() $k$-rational points by the formula [Reference WeilWei12, Theorem 2.2.5]
$k$-rational points by the formula [Reference WeilWei12, Theorem 2.2.5]
Remark 3.1.5 If ![]() ${\mathcal {M}}$ is a Deligne–Mumford stack, then
${\mathcal {M}}$ is a Deligne–Mumford stack, then ![]() $\pi :{\mathcal {M}} \to M$ is proper [Reference Keel and MoriKM97] and, thus, Assumption 3.1.1 is automatically satisfied. In this case
$\pi :{\mathcal {M}} \to M$ is proper [Reference Keel and MoriKM97] and, thus, Assumption 3.1.1 is automatically satisfied. In this case ![]() $\mu _{\rm can}$ agrees with the orbifold measure constructed in [Reference Groechenig, Wyss and ZieglerGWZ20a, § 2.3], although in [Reference Groechenig, Wyss and ZieglerGWZ20a, § 2.3] there is no assumption on the codimension of the complement of
$\mu _{\rm can}$ agrees with the orbifold measure constructed in [Reference Groechenig, Wyss and ZieglerGWZ20a, § 2.3], although in [Reference Groechenig, Wyss and ZieglerGWZ20a, § 2.3] there is no assumption on the codimension of the complement of ![]() $U \subset {\mathcal {M}}$. If
$U \subset {\mathcal {M}}$. If ![]() ${\mathcal {M}}$ is tame, the total volume of
${\mathcal {M}}$ is tame, the total volume of ![]() $M^\natural$ can be expressed as a weighted point count of the twisted inertia stack of
$M^\natural$ can be expressed as a weighted point count of the twisted inertia stack of ![]() ${\mathcal {M}}$ (see [Reference Groechenig, Wyss and ZieglerGWZ20a, Theorem 2.21]).
${\mathcal {M}}$ (see [Reference Groechenig, Wyss and ZieglerGWZ20a, Theorem 2.21]).
Remark 3.1.6 Groechenig pointed out to us the following alternative construction: let ![]() ${\mathcal {M}}/{\mathcal {O}}$ be any finite-type Artin stack of relative dimension
${\mathcal {M}}/{\mathcal {O}}$ be any finite-type Artin stack of relative dimension ![]() $n$ with a morphism
$n$ with a morphism ![]() $\pi :{\mathcal {M}} \to M$ to a scheme
$\pi :{\mathcal {M}} \to M$ to a scheme ![]() $M$. Assume, furthermore, that there exists a smooth stabilizer-free open
$M$. Assume, furthermore, that there exists a smooth stabilizer-free open ![]() $U \subset {\mathcal {M}}$ such that
$U \subset {\mathcal {M}}$ such that ![]() $\pi _{|U}$ is an isomorphism onto its image and that Assumption 3.1.1 is satisfied. Finally, suppose that there exists a line bundle
$\pi _{|U}$ is an isomorphism onto its image and that Assumption 3.1.1 is satisfied. Finally, suppose that there exists a line bundle ![]() $\widetilde {\mathcal {K}}$ on
$\widetilde {\mathcal {K}}$ on ![]() ${\mathcal {M}}$ which restricts to a power of the canonical line bundle
${\mathcal {M}}$ which restricts to a power of the canonical line bundle ![]() $\mathcal {K}_{U/{\mathcal {O}}}$ on
$\mathcal {K}_{U/{\mathcal {O}}}$ on ![]() $U$. Then as in [Reference YasudaYas17, § 4.1], integrating a suitable root of the absolute value of local sections of
$U$. Then as in [Reference YasudaYas17, § 4.1], integrating a suitable root of the absolute value of local sections of ![]() $\widetilde {\mathcal {K}}$ against the Haar measure defines a measure
$\widetilde {\mathcal {K}}$ against the Haar measure defines a measure ![]() $\mu ^{vir}$ on
$\mu ^{vir}$ on ![]() $M^\natural$ by an argument as in Proposition 3.1.2. By construction, if both
$M^\natural$ by an argument as in Proposition 3.1.2. By construction, if both ![]() $\mu ^{vir}$ and
$\mu ^{vir}$ and ![]() $\mu _{\rm can}$ are defined they coincide.
$\mu _{\rm can}$ are defined they coincide.
Interestingly, in the context of moduli spaces ![]() ${\mathbb {M}}$ of sheaves on a surface
${\mathbb {M}}$ of sheaves on a surface ![]() $S$, such a line bundle
$S$, such a line bundle ![]() $\widetilde {\mathcal {K}}$ arises from the deformation theory as the determinant of
$\widetilde {\mathcal {K}}$ arises from the deformation theory as the determinant of ![]() $\bf {R}\mathcal {H}om_{{\mathbb {M}}}(\mathcal {F},\mathcal {F})$, where
$\bf {R}\mathcal {H}om_{{\mathbb {M}}}(\mathcal {F},\mathcal {F})$, where ![]() $\mathcal {F}$ is the universal sheaf on
$\mathcal {F}$ is the universal sheaf on ![]() $S\times {\mathbb {M}}$ (see [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15] for the definition in the strictly semi-stable case, or [Reference Huybrechts and LehnHL97, § 8.3] for a simpler explanation on the locus of stables).
$S\times {\mathbb {M}}$ (see [Reference Ben-Bassat, Brav, Bussi and JoyceBBBJ15] for the definition in the strictly semi-stable case, or [Reference Huybrechts and LehnHL97, § 8.3] for a simpler explanation on the locus of stables).
3.2 The canonical measure on moduli spaces of sheaves
Let ![]() $S$ be a smooth projective relative surface over
$S$ be a smooth projective relative surface over ![]() $\mathsf {Spec}({\mathcal {O}})$ and
$\mathsf {Spec}({\mathcal {O}})$ and ![]() ${\mathcal {M}}_{\beta,\chi }$ the
${\mathcal {M}}_{\beta,\chi }$ the ![]() ${\mathbb {G}}_m$-rigidified moduli stack of semi-stable one-dimensional sheaves on
${\mathbb {G}}_m$-rigidified moduli stack of semi-stable one-dimensional sheaves on ![]() $S$ with moduli space
$S$ with moduli space ![]() $\operatorname {M}_{\beta,\chi }$ as in § 2.
$\operatorname {M}_{\beta,\chi }$ as in § 2.
We take the open substacks ![]() $\mathcal {U}_{\beta,\chi }^{st}\subset \mathcal {U}_{\beta,\chi }\subset {\mathcal {M}}_{\beta,\chi }$ of geometrically stable line bundles and of line bundles, respectively, as substacks
$\mathcal {U}_{\beta,\chi }^{st}\subset \mathcal {U}_{\beta,\chi }\subset {\mathcal {M}}_{\beta,\chi }$ of geometrically stable line bundles and of line bundles, respectively, as substacks ![]() $U\subset U'$ in the notation of § 3.1. From now on we always assume that
$U\subset U'$ in the notation of § 3.1. From now on we always assume that ![]() $S \to \mathsf {Spec}({\mathcal {O}})$ is either a smooth projective del Pezzo surface or a K3 surface satisfying Assumption 3.2.1.
$S \to \mathsf {Spec}({\mathcal {O}})$ is either a smooth projective del Pezzo surface or a K3 surface satisfying Assumption 3.2.1.
Assumption 3.2.1 Let ![]() $S \to \mathsf {Spec}({\mathcal {O}})$ be a smooth projective K3 surface and
$S \to \mathsf {Spec}({\mathcal {O}})$ be a smooth projective K3 surface and ![]() $(\beta,\chi )$ a dimension vector such that the following hold.
$(\beta,\chi )$ a dimension vector such that the following hold.
(i) The locus of
 $\mathcal {U}_{\beta,\chi } \subseteq \mathbb {M}_{\beta,\chi }(S)$ of line bundles has complement of codimension at least two and
$\mathcal {U}_{\beta,\chi } \subseteq \mathbb {M}_{\beta,\chi }(S)$ of line bundles has complement of codimension at least two and  $\mathcal {U}_{\beta,\chi }^{st}$ is non-empty.
$\mathcal {U}_{\beta,\chi }^{st}$ is non-empty.(ii) The moduli stack
 $\mathbb {M}_{\beta,\chi }(S)$ is normal.
$\mathbb {M}_{\beta,\chi }(S)$ is normal.
Remark 3.2.2 We have already commented on the restriction that Assumption 3.2.1(i) imposes in Remark 2.1.8. Over ![]() ${\mathbb {C}}$, it follows from Theorem 2.1.7 that Assumption 3.2.1(i) implies Assumption 3.2.1(ii), but we do not know of a proof over more general bases. However, by choosing a suitable spreading out
${\mathbb {C}}$, it follows from Theorem 2.1.7 that Assumption 3.2.1(i) implies Assumption 3.2.1(ii), but we do not know of a proof over more general bases. However, by choosing a suitable spreading out ![]() $S \to \mathsf {Spec}(B)$ of a complex K3 surface, satisfying Assumption 3.2.1(i), over the spectrum of a finitely generated
$S \to \mathsf {Spec}(B)$ of a complex K3 surface, satisfying Assumption 3.2.1(i), over the spectrum of a finitely generated ![]() ${\mathbb {Z}}$-algebra
${\mathbb {Z}}$-algebra ![]() $B$ we obtain finite-type moduli stacks
$B$ we obtain finite-type moduli stacks ![]() $\phi : {\mathbb {M}}_{\beta,\chi } \to \mathsf {Spec}(B)$ by Theorem 2.1.3. Then Theorem 2.1.7 implies that the generic fiber of
$\phi : {\mathbb {M}}_{\beta,\chi } \to \mathsf {Spec}(B)$ by Theorem 2.1.3. Then Theorem 2.1.7 implies that the generic fiber of ![]() $\phi$ is geometrically normal and, thus, by [Reference GrothendieckGro66, Theorem 12.1.6, Corollary 9.5.2], the fibers of
$\phi$ is geometrically normal and, thus, by [Reference GrothendieckGro66, Theorem 12.1.6, Corollary 9.5.2], the fibers of ![]() $\phi$ are normal on a non-empty open
$\phi$ are normal on a non-empty open ![]() $V \subset \mathsf {Spec}(B)$. Thus, by pulling back
$V \subset \mathsf {Spec}(B)$. Thus, by pulling back ![]() $S$ along regular points
$S$ along regular points ![]() $\mathsf {Spec}({\mathcal {O}}) \to V$, with
$\mathsf {Spec}({\mathcal {O}}) \to V$, with ![]() ${\mathcal {O}}$ the ring of integers of a non-archimedean local field, we obtain many examples of relative K3 surfaces over
${\mathcal {O}}$ the ring of integers of a non-archimedean local field, we obtain many examples of relative K3 surfaces over ![]() $\mathsf {Spec}({\mathcal {O}})$ where Assumption 3.2.1 holds [Reference GrothendieckGro65, Proposition 6.14.1].
$\mathsf {Spec}({\mathcal {O}})$ where Assumption 3.2.1 holds [Reference GrothendieckGro65, Proposition 6.14.1].
By Theorem 2.1.3, Lemma 2.1.4 and Proposition 2.2.1 all the assumptions for Proposition 3.1.2 to hold are satisfied and we obtain a canonical measure ![]() $\mu _{\rm can}$ on
$\mu _{\rm can}$ on ![]() $\operatorname {M}_{\beta,\chi }^\natural$.
$\operatorname {M}_{\beta,\chi }^\natural$.
Also, the smooth base ![]() $B$ of the Hilbert–Chow morphism
$B$ of the Hilbert–Chow morphism ![]() $h_\chi :\operatorname {M}_{\beta,\chi } \to B$ admits a canonical measure
$h_\chi :\operatorname {M}_{\beta,\chi } \to B$ admits a canonical measure ![]() $\mu _{{\rm can},B}$ and it will be useful later to have an explicit description of the relative measure
$\mu _{{\rm can},B}$ and it will be useful later to have an explicit description of the relative measure ![]() $\mu _{\rm can}/\mu _{{\rm can},B}$ on smooth fibers of
$\mu _{\rm can}/\mu _{{\rm can},B}$ on smooth fibers of ![]() $h_\chi$, as in [Reference Groechenig, Wyss and ZieglerGWZ20b, § 6.3].
$h_\chi$, as in [Reference Groechenig, Wyss and ZieglerGWZ20b, § 6.3].
Lemma 3.2.3 Let ![]() $b \in B({\mathcal {O}})$ be such that the pullback of the universal curve
$b \in B({\mathcal {O}})$ be such that the pullback of the universal curve ![]() ${\mathcal {C}}_b \to \mathsf {Spec}({\mathcal {O}})$ is generically smooth. Then under the identification of
${\mathcal {C}}_b \to \mathsf {Spec}({\mathcal {O}})$ is generically smooth. Then under the identification of ![]() $h_\chi ^{-1}(b)(F)$ with
$h_\chi ^{-1}(b)(F)$ with ![]() $\mathrm {Pic}^{d}_{{\mathcal {C}}_b}(F)$, for
$\mathrm {Pic}^{d}_{{\mathcal {C}}_b}(F)$, for ![]() $d = \chi + g-1$, the relative measure
$d = \chi + g-1$, the relative measure ![]() $\mu _{\rm can}/\mu _{{\rm can},B}$ on
$\mu _{\rm can}/\mu _{{\rm can},B}$ on ![]() $h_\chi ^{-1}(b)(F)$ is given by integrating the absolute valued of a translation-invariant gauge form
$h_\chi ^{-1}(b)(F)$ is given by integrating the absolute valued of a translation-invariant gauge form ![]() $\omega _b$ on the
$\omega _b$ on the ![]() $\mathrm {Pic}^{0}_{{\mathcal {C}}_b}$-torsor
$\mathrm {Pic}^{0}_{{\mathcal {C}}_b}$-torsor ![]() $\mathrm {Pic}^{d}_{{\mathcal {C}}_b}$.
$\mathrm {Pic}^{d}_{{\mathcal {C}}_b}$.
Proof. Let ![]() $\pi : \operatorname {Pic}^{{\rm totdeg}=0}_{\mathcal {C} /B}\to B$ be the smooth group scheme of total degree-zero line bundles on a flat family
$\pi : \operatorname {Pic}^{{\rm totdeg}=0}_{\mathcal {C} /B}\to B$ be the smooth group scheme of total degree-zero line bundles on a flat family ![]() $\mathcal {C}\rightarrow B$ of curves. By [Reference Bosch, Lütkebohmert and RaynaudBLR12, § 4.2] it admits, up to replacing
$\mathcal {C}\rightarrow B$ of curves. By [Reference Bosch, Lütkebohmert and RaynaudBLR12, § 4.2] it admits, up to replacing ![]() $B$ with a neighborhood of
$B$ with a neighborhood of ![]() $b\in B$, a global, translation-invariant, trivializing section
$b\in B$, a global, translation-invariant, trivializing section ![]() $\omega _{{\rm rel}}$ of
$\omega _{{\rm rel}}$ of ![]() $\Omega ^g_{\operatorname {Pic}^{{\rm totdeg}=0}/B}$. In particular,
$\Omega ^g_{\operatorname {Pic}^{{\rm totdeg}=0}/B}$. In particular, ![]() $\operatorname {Pic}^{{\rm totdeg}=0}_{\mathcal {C} /B}/\mathcal {O}_F$ has a volume form
$\operatorname {Pic}^{{\rm totdeg}=0}_{\mathcal {C} /B}/\mathcal {O}_F$ has a volume form ![]() $\omega =\pi ^*\omega _B\wedge \omega _{{\rm rel}}$, where
$\omega =\pi ^*\omega _B\wedge \omega _{{\rm rel}}$, where ![]() $\omega _B$ is a volume form in a neighborhood of
$\omega _B$ is a volume form in a neighborhood of ![]() $b\in B$ inducing
$b\in B$ inducing ![]() $\mu _{{\rm can},B}$.
$\mu _{{\rm can},B}$.
By [Reference Groechenig, Wyss and ZieglerGWZ20b, Lemma 6.13], since ![]() $\operatorname {Pic}^{{\rm totdeg}=d}_{\mathcal {C} /B}$ is a torsor under the group scheme of total degree-zero line bundles, the relative form
$\operatorname {Pic}^{{\rm totdeg}=d}_{\mathcal {C} /B}$ is a torsor under the group scheme of total degree-zero line bundles, the relative form ![]() $\omega _{{\rm rel}}$ induces a section
$\omega _{{\rm rel}}$ induces a section ![]() $\widetilde {\omega }_{{\rm rel}}$ of
$\widetilde {\omega }_{{\rm rel}}$ of ![]() $\Omega ^g_{\operatorname {Pic}^{{\rm totdeg}=d}/B };$ we thus have a volume form
$\Omega ^g_{\operatorname {Pic}^{{\rm totdeg}=d}/B };$ we thus have a volume form ![]() $\omega _d=\pi ^*\omega _B\wedge \widetilde {\omega }_{{\rm rel}}$ on
$\omega _d=\pi ^*\omega _B\wedge \widetilde {\omega }_{{\rm rel}}$ on ![]() $\operatorname {Pic}^{{\rm totdeg}=d}_{\mathcal {C} /B}$.
$\operatorname {Pic}^{{\rm totdeg}=d}_{\mathcal {C} /B}$.
Since ![]() ${\mathcal {U}}_{\beta,\chi }$ has complement of codimension at least two in
${\mathcal {U}}_{\beta,\chi }$ has complement of codimension at least two in ![]() ${\mathcal {M}}_{\beta,\chi }$ by Proposition 2.2.1, integrating the absolute value of
${\mathcal {M}}_{\beta,\chi }$ by Proposition 2.2.1, integrating the absolute value of ![]() $\omega _d$ computes
$\omega _d$ computes ![]() $\mu _{\rm can}$. Therefore, on
$\mu _{\rm can}$. Therefore, on ![]() $h_\chi ^{-1}(b)(F)$ the relative measure
$h_\chi ^{-1}(b)(F)$ the relative measure ![]() $\mu _{\rm can}/\mu _{{\rm can},B}$ is given by integrating the absolute value of
$\mu _{\rm can}/\mu _{{\rm can},B}$ is given by integrating the absolute value of ![]() $\omega _b = \widetilde {\omega }_{{\rm rel},b}$.
$\omega _b = \widetilde {\omega }_{{\rm rel},b}$.
An analogous construction can be done for moduli spaces of Higgs bundles using Theorem 2.3.1.
4. Gerbes and Tate duality
4.1  ${\mathbb {G}}_m$ gerbes
${\mathbb {G}}_m$ gerbes
Let ![]() $X\to V$ be a stack for the fppf-topology. Then
$X\to V$ be a stack for the fppf-topology. Then ![]() $X$ is said to be a gerbe if:
$X$ is said to be a gerbe if:
(i) for every scheme
 $T$ over
$T$ over  $V$ and objects
$V$ and objects  $x,y \in X(T)$, there exists some fppf-cover
$x,y \in X(T)$, there exists some fppf-cover  $f\colon U \to T$ and an isomorphism
$f\colon U \to T$ and an isomorphism  $x_{|U}\cong y_{|U}$;
$x_{|U}\cong y_{|U}$;(ii) there exists an fppf-cover
 $U\to V$ such that the groupoid
$U\to V$ such that the groupoid  $X(U)$ is non-empty.
$X(U)$ is non-empty.
For every ![]() $T\to V$ and isomorphism
$T\to V$ and isomorphism ![]() $\phi \colon x \to y$ in
$\phi \colon x \to y$ in ![]() $X(T)$, conjugation by
$X(T)$, conjugation by ![]() $\phi$ induces an isomorphism
$\phi$ induces an isomorphism ![]() $\mathsf {Aut}_T(x)\to \mathsf {Aut}_T(y)$. Suppose that every object of
$\mathsf {Aut}_T(x)\to \mathsf {Aut}_T(y)$. Suppose that every object of ![]() $X$ has abelian automorphism group in its fiber category; in this case we say that the gerbe
$X$ has abelian automorphism group in its fiber category; in this case we say that the gerbe ![]() $X\to V$ is abelian. Then for every
$X\to V$ is abelian. Then for every ![]() $T\to V$ and objects
$T\to V$ and objects ![]() $x,y \in X(T)$, there is a canonical isomorphism
$x,y \in X(T)$, there is a canonical isomorphism ![]() $\mathsf {Aut}_T(x)\cong \mathsf {Aut}_T(y)$. These isomorphisms determine a sheaf of groups
$\mathsf {Aut}_T(x)\cong \mathsf {Aut}_T(y)$. These isomorphisms determine a sheaf of groups ![]() $Band(X/V)$ over
$Band(X/V)$ over ![]() $V$.
$V$.
We say that an abelian gerbe ![]() $X \rightarrow V$ is a
$X \rightarrow V$ is a ![]() ${\mathbb {G}}_m$ gerbe if there is an isomorphism
${\mathbb {G}}_m$ gerbe if there is an isomorphism ![]() ${\mathbb {G}}_{m,V}\to Band(X/V)$.
${\mathbb {G}}_{m,V}\to Band(X/V)$.
By [Reference GiraudGir20] equivalence classes of ![]() ${\mathbb {G}}_m$ gerbes on
${\mathbb {G}}_m$ gerbes on ![]() $V$ are in bijection with the group
$V$ are in bijection with the group ![]() $H^2(V_{fppf},{\mathbb {G}}_m)$, the Brauer group of
$H^2(V_{fppf},{\mathbb {G}}_m)$, the Brauer group of ![]() $V$. A gerbe
$V$. A gerbe ![]() $X/V$ is trivial if it is equivalent to
$X/V$ is trivial if it is equivalent to ![]() $[X/{\mathbb {G}}_{m,V}]$, where
$[X/{\mathbb {G}}_{m,V}]$, where ![]() ${\mathbb {G}}_{m,V}$ acts trivially on
${\mathbb {G}}_{m,V}$ acts trivially on ![]() $X$.
$X$.
We recall that for ![]() $F$ a local field, the Brauer group
$F$ a local field, the Brauer group ![]() $H^2(F_{fppf},{\mathbb {G}}_m)$ is isomorphic to
$H^2(F_{fppf},{\mathbb {G}}_m)$ is isomorphic to ![]() $\mathbb {Q}/\mathbb {Z}$ by mean of the Hasse invariant; see, for example, [Reference SerreSer68, Proposition XIII.6].
$\mathbb {Q}/\mathbb {Z}$ by mean of the Hasse invariant; see, for example, [Reference SerreSer68, Proposition XIII.6].
Given ![]() $X/V$ a
$X/V$ a ![]() ${\mathbb {G}}_m$ gerbe, for any point
${\mathbb {G}}_m$ gerbe, for any point ![]() $F\xrightarrow {s} V$ we get a
$F\xrightarrow {s} V$ we get a ![]() ${\mathbb {G}}_m$ gerbe
${\mathbb {G}}_m$ gerbe ![]() $s^*X/F$ by pullback. This defines a complex valued function:
$s^*X/F$ by pullback. This defines a complex valued function:
4.2 Picard stacks/schemes of curves
Let ![]() $V$ be a scheme and
$V$ be a scheme and ![]() $c\colon X\to V$ a smooth proper curveFootnote 3 with fibers of genus
$c\colon X\to V$ a smooth proper curveFootnote 3 with fibers of genus ![]() $g\geq 0$.
$g\geq 0$.
We denote by ![]() $\mathfrak {Pic}_{X/V}$ the Picard stack of
$\mathfrak {Pic}_{X/V}$ the Picard stack of ![]() $X/V$; in other words, for an
$X/V$; in other words, for an ![]() $V$-scheme
$V$-scheme ![]() $T$,
$T$, ![]() $\mathfrak {Pic}_{X/V}(T)$ is the groupoid of invertible sheaves on
$\mathfrak {Pic}_{X/V}(T)$ is the groupoid of invertible sheaves on ![]() $X\times _VT$. The group of isomorphism classes of objects of
$X\times _VT$. The group of isomorphism classes of objects of ![]() $\mathfrak {Pic}_{X/V}(T)$ is therefore the classical Picard group
$\mathfrak {Pic}_{X/V}(T)$ is therefore the classical Picard group ![]() $\mathrm {Pic}(X\times _VT)$. For each integer
$\mathrm {Pic}(X\times _VT)$. For each integer ![]() $d$, we denote by
$d$, we denote by ![]() $\mathfrak {Pic}^d_{X/V}$ the substack of line bundles of degree
$\mathfrak {Pic}^d_{X/V}$ the substack of line bundles of degree ![]() $d$.
$d$.
We denote by ![]() $\mathrm {Pic}_{X/V}$ the sheaf
$\mathrm {Pic}_{X/V}$ the sheaf ![]() $R^1_{fppf}c_*{\mathbb {G}}_m$ on
$R^1_{fppf}c_*{\mathbb {G}}_m$ on ![]() $V$; it can be equivalently defined as the sheafification of the presheaf
$V$; it can be equivalently defined as the sheafification of the presheaf ![]() $T \mapsto \mathrm {Pic}(X\times _VT)$. The natural morphism
$T \mapsto \mathrm {Pic}(X\times _VT)$. The natural morphism
is a gerbe [Sta, 0DME] banded by ![]() ${\mathbb {G}}_m$.
${\mathbb {G}}_m$.
The degree-map factors through ![]() $\alpha$ and we denote by
$\alpha$ and we denote by ![]() $\mathrm {Pic}^d_{X/V}$ the corresponding component of degree
$\mathrm {Pic}^d_{X/V}$ the corresponding component of degree ![]() $d$ line bundles. The degree-zero part
$d$ line bundles. The degree-zero part ![]() $\mathrm {Pic}^0_{X/V}$ is represented by an abelian scheme of relative dimension
$\mathrm {Pic}^0_{X/V}$ is represented by an abelian scheme of relative dimension ![]() $g$, the relative Jacobian, and each
$g$, the relative Jacobian, and each ![]() $\mathrm {Pic}^d_{X/V}$ is an
$\mathrm {Pic}^d_{X/V}$ is an ![]() $V$-torsor under it.
$V$-torsor under it.
In general, a ![]() $T$-point of
$T$-point of ![]() $\mathrm {Pic}_{X/V}$ need not correspond to a line bundle on
$\mathrm {Pic}_{X/V}$ need not correspond to a line bundle on ![]() $X\times _VT$; this property gets lost when the sheafification of
$X\times _VT$; this property gets lost when the sheafification of ![]() $T\mapsto \mathrm {Pic}(X\times _VT)$ is taken.
$T\mapsto \mathrm {Pic}(X\times _VT)$ is taken.
Lemma 4.2.2 [Reference Bosch, Lütkebohmert and RaynaudBLR12, Proposition 8.4]
For every ![]() $V$-scheme
$V$-scheme ![]() $T$, there is a canonical exact sequence of abelian groups, functorial in
$T$, there is a canonical exact sequence of abelian groups, functorial in ![]() $T$,
$T$,
Since in our case ![]() $\mathrm {Pic}_{X/V}$ is a
$\mathrm {Pic}_{X/V}$ is a ![]() $V$-scheme, we may look at the particular case
$V$-scheme, we may look at the particular case ![]() $T=\mathrm {Pic}_{X/V}$. Then the identity in
$T=\mathrm {Pic}_{X/V}$. Then the identity in ![]() $\mathrm {Pic}_{X/V}(\mathrm {Pic}_{X/V})$ gets mapped to the element of
$\mathrm {Pic}_{X/V}(\mathrm {Pic}_{X/V})$ gets mapped to the element of ![]() $H^2(\mathrm {Pic}_{X/V},{\mathbb {G}}_m)$ corresponding to the
$H^2(\mathrm {Pic}_{X/V},{\mathbb {G}}_m)$ corresponding to the ![]() ${\mathbb {G}}_m$ gerbe
${\mathbb {G}}_m$ gerbe ![]() $\alpha$ of (4.2.1). By Lemma 4.2.2,
$\alpha$ of (4.2.1). By Lemma 4.2.2, ![]() $\alpha$ is trivial if and only if there is a universal Poincaré bundle
$\alpha$ is trivial if and only if there is a universal Poincaré bundle ![]() $\mathcal {L}$ on
$\mathcal {L}$ on ![]() $X\times _V\mathrm {Pic}_{X/V}$. For example, this is the case when
$X\times _V\mathrm {Pic}_{X/V}$. For example, this is the case when ![]() $X\to V$ has a section, since then the map
$X\to V$ has a section, since then the map
is injective.
More generally, for an ![]() $V$-scheme
$V$-scheme ![]() $T$, the map
$T$, the map ![]() $c_T\colon \mathrm {Pic}_{X/V}(T) \to H^2(T,{\mathbb {G}}_m)$ sends
$c_T\colon \mathrm {Pic}_{X/V}(T) \to H^2(T,{\mathbb {G}}_m)$ sends ![]() $x\colon T\to \mathrm {Pic}_{X/V}$ to the equivalence class of the
$x\colon T\to \mathrm {Pic}_{X/V}$ to the equivalence class of the ![]() ${\mathbb {G}}_m$ gerbe on
${\mathbb {G}}_m$ gerbe on ![]() $T$ obtained by pulling back
$T$ obtained by pulling back ![]() $\alpha$ along
$\alpha$ along ![]() $x$. Such a gerbe is trivial if and only if
$x$. Such a gerbe is trivial if and only if ![]() $x$ comes from a line bundle on
$x$ comes from a line bundle on ![]() $X\times _VT$ (that is, is in the essential image of
$X\times _VT$ (that is, is in the essential image of ![]() $\alpha$).
$\alpha$).
4.3 Tate duality
We consider now the special case where the base ![]() $V$ is the spectrum of a non-archimedean local field
$V$ is the spectrum of a non-archimedean local field ![]() $F$. As recalled above, the Brauer group
$F$. As recalled above, the Brauer group ![]() $H^2(F,{\mathbb {G}}_m)$ is identified with
$H^2(F,{\mathbb {G}}_m)$ is identified with ![]() ${\mathbb {Q}}/{\mathbb {Z}}$ via the Hasse invariant. We denote by
${\mathbb {Q}}/{\mathbb {Z}}$ via the Hasse invariant. We denote by ![]() $f\colon \mathrm {Pic}_{X/F}(F)\to {\mathbb {Q}}/{\mathbb {Z}}$ the group homomorphism of Lemma 4.2.2, and for each integer
$f\colon \mathrm {Pic}_{X/F}(F)\to {\mathbb {Q}}/{\mathbb {Z}}$ the group homomorphism of Lemma 4.2.2, and for each integer ![]() $d\in {\mathbb {Z}}$, we call
$d\in {\mathbb {Z}}$, we call ![]() $f_d\colon \mathrm {Pic}^d_{X/F}(F)\to {\mathbb {Q}}/{\mathbb {Z}}$ the restriction of
$f_d\colon \mathrm {Pic}^d_{X/F}(F)\to {\mathbb {Q}}/{\mathbb {Z}}$ the restriction of ![]() $f$.
$f$.
Note that any ![]() $x \in \mathrm {Pic}^d_{X/F}(F)$ gives rise to an isomorphism
$x \in \mathrm {Pic}^d_{X/F}(F)$ gives rise to an isomorphism ![]() $s_x: \mathrm {Pic}^0_{X/F} \to \mathrm {Pic}^d_{X/F}$ and since
$s_x: \mathrm {Pic}^0_{X/F} \to \mathrm {Pic}^d_{X/F}$ and since ![]() $f$ is a group homomorphism we have
$f$ is a group homomorphism we have
The following proposition gives some control over ![]() $f_0$ in terms of torsor instead of gerbes.
$f_0$ in terms of torsor instead of gerbes.
Proposition 4.3.2 The image of ![]() $f_0$ is
$f_0$ is ![]() $(({1}/{d_0}){\mathbb {Z}})/{\mathbb {Z}}$, where
$(({1}/{d_0}){\mathbb {Z}})/{\mathbb {Z}}$, where ![]() $d_0$ is the smallest positive integer for which
$d_0$ is the smallest positive integer for which ![]() $\mathrm {Pic}^{d_0}_{X/F}(F)$ is non-empty.
$\mathrm {Pic}^{d_0}_{X/F}(F)$ is non-empty.
In particular, ![]() $f_0$ is constant if and only if
$f_0$ is constant if and only if ![]() $\mathrm {Pic}^{1}_{X/F}(F)$ is non-empty.
$\mathrm {Pic}^{1}_{X/F}(F)$ is non-empty.
Similar statements have been used crucially in [Reference Groechenig, Wyss and ZieglerGWZ20b, Reference Groechenig, Wyss and ZieglerGWZ20a] and the following discussion is essentially taken from there.
The proof of Proposition 4.3.2 relies on Tate duality over local fields. Let ![]() $A$ be an abelian variety over
$A$ be an abelian variety over ![]() $F$ and
$F$ and ![]() $A^t$ its dual.
$A^t$ its dual.
Theorem 4.3.3 [Reference MilneMil86, Theorem 3.7.8]
There is a canonical perfect pairing
The pairing admits the following geometric description, see [Reference Groechenig, Wyss and ZieglerGWZ20b, Remark 3.11]. First from [Reference MilneMil86, Lemma 3.1] we have an isomorphism
Now, working in the category of commutative group stacks considered in [Reference BrochardBro21], elements of ![]() $\mathsf {Ext}^2(A,{\mathbb {G}}_m)$ can be represented by
$\mathsf {Ext}^2(A,{\mathbb {G}}_m)$ can be represented by ![]() ${\mathbb {G}}_m$ gerbes on
${\mathbb {G}}_m$ gerbes on ![]() $A$ with a group structure.
$A$ with a group structure.
Given ![]() $x \in \mathsf {A}(F)$,
$x \in \mathsf {A}(F)$, ![]() $\tau \in H^{1}(F,A^t)$ and
$\tau \in H^{1}(F,A^t)$ and ![]() $\alpha _\tau \in \mathsf {Ext}^2(A,{\mathbb {G}}_m)$ the image of
$\alpha _\tau \in \mathsf {Ext}^2(A,{\mathbb {G}}_m)$ the image of ![]() $\tau$ under (4.3.4), the paring of
$\tau$ under (4.3.4), the paring of ![]() $x$ with
$x$ with ![]() $\tau$ from Theorem 4.3.3 equals the class of the
$\tau$ from Theorem 4.3.3 equals the class of the ![]() ${\mathbb {G}}_m$ gerbe
${\mathbb {G}}_m$ gerbe ![]() $x^*\alpha _\tau$ on
$x^*\alpha _\tau$ on ![]() $\mathsf {Spec}(F)$ under the Hasse invariant isomorphism
$\mathsf {Spec}(F)$ under the Hasse invariant isomorphism ![]() $H^2(F,{\mathbb {G}}_m) \cong {\mathbb {Q}}/{\mathbb {Z}}$.
$H^2(F,{\mathbb {G}}_m) \cong {\mathbb {Q}}/{\mathbb {Z}}$.
Thus, for ![]() $A= \mathrm {Pic}^0_{X/F} = A^t$ the homomorphism
$A= \mathrm {Pic}^0_{X/F} = A^t$ the homomorphism ![]() $f_0$ is simply the Tate-duality pairing with the
$f_0$ is simply the Tate-duality pairing with the ![]() ${\mathbb {G}}_m$ gerbe
${\mathbb {G}}_m$ gerbe ![]() $\alpha _0: \mathfrak {Pic}^0_{X/F} \rightarrow \mathrm {Pic}^0_{X/F}$.
$\alpha _0: \mathfrak {Pic}^0_{X/F} \rightarrow \mathrm {Pic}^0_{X/F}$.
Proof of Proposition 4.3.2 To simplify the notation we drop the subscript ![]() $X/F$. By the previous discussion and Theorem 4.3.3 we see that
$X/F$. By the previous discussion and Theorem 4.3.3 we see that ![]() $d_0\cdot f_0 \equiv 0$ if and only if
$d_0\cdot f_0 \equiv 0$ if and only if ![]() $\alpha _0^{d_0}$ is equivalent to the trivial
$\alpha _0^{d_0}$ is equivalent to the trivial ![]() ${\mathbb {G}}_m$ gerbe on
${\mathbb {G}}_m$ gerbe on ![]() $\mathrm {Pic}^0$. We thus need to show that the latter holds if and only if
$\mathrm {Pic}^0$. We thus need to show that the latter holds if and only if ![]() $\mathrm {Pic}^{d_0}(F)$ is non-empty.
$\mathrm {Pic}^{d_0}(F)$ is non-empty.
We consider the category of dualizable commutative group stacks ![]() $\mathrm {DCGS}_F$ over
$\mathrm {DCGS}_F$ over ![]() $\mathsf {Spec}(F)$; see, for example, [Reference BrochardBro21] for a detailed account. The internal hom-functor
$\mathsf {Spec}(F)$; see, for example, [Reference BrochardBro21] for a detailed account. The internal hom-functor ![]() $D(\cdot ) = \mathcal {H}om(\cdot,B\mathbb {G}_m)$ induces an anti-equivalence on
$D(\cdot ) = \mathcal {H}om(\cdot,B\mathbb {G}_m)$ induces an anti-equivalence on ![]() $\mathrm {DCGS}_F$ satisfying
$\mathrm {DCGS}_F$ satisfying ![]() $D\circ D = Id$ and extending the usual duality functor on abelian varieties. Furthermore, there is an auto-equivalence
$D\circ D = Id$ and extending the usual duality functor on abelian varieties. Furthermore, there is an auto-equivalence ![]() $D(\mathfrak {Pic}) \cong \mathfrak {Pic}$ (see [Reference TravkinTra16, § 3.2]). Thus, applying
$D(\mathfrak {Pic}) \cong \mathfrak {Pic}$ (see [Reference TravkinTra16, § 3.2]). Thus, applying ![]() $D$ to the short exact sequence
$D$ to the short exact sequence
we get the sequence
Here exactness on the right follows from [Reference BrochardBro21, Proposition 3.18] and the fact that ![]() $\mathcal {E}xt^2(\mathrm {Pic})=0$ (see [Reference BrochardBro21, Corollary 11.5]). Since
$\mathcal {E}xt^2(\mathrm {Pic})=0$ (see [Reference BrochardBro21, Corollary 11.5]). Since ![]() $\beta$ is an epimorphism with kernel
$\beta$ is an epimorphism with kernel ![]() $\mathfrak {Pic}^0$ we get an equivalence
$\mathfrak {Pic}^0$ we get an equivalence ![]() $D(\mathrm {Pic}) \cong \mathfrak {Pic}^0$. From this we deduce that the sequences
$D(\mathrm {Pic}) \cong \mathfrak {Pic}^0$. From this we deduce that the sequences
are exchanged by duality.
Now (4.3.5) is the extension of ![]() ${\mathbb {Z}}$ by
${\mathbb {Z}}$ by ![]() $\mathrm {Pic}^0$ corresponding to the
$\mathrm {Pic}^0$ corresponding to the ![]() $\mathrm {Pic}^0$-torsor
$\mathrm {Pic}^0$-torsor ![]() $\mathrm {Pic}^1$ under the equivalence [Reference BrochardBro21, Proposition 5.8]. In particular,
$\mathrm {Pic}^1$ under the equivalence [Reference BrochardBro21, Proposition 5.8]. In particular, ![]() $\mathrm {Pic}^1$ has a rational point if and only (4.3.5) splits. Dually (4.3.6) is the
$\mathrm {Pic}^1$ has a rational point if and only (4.3.5) splits. Dually (4.3.6) is the ![]() $B{\mathbb {G}}_m$-torsor on
$B{\mathbb {G}}_m$-torsor on ![]() $\mathrm {Pic}^0$ corresponding to
$\mathrm {Pic}^0$ corresponding to ![]() $\alpha _0$ under the equivalence [Reference BrochardBro21, Proposition 5.11] and splits if and only if
$\alpha _0$ under the equivalence [Reference BrochardBro21, Proposition 5.11] and splits if and only if ![]() $\alpha _0$ is trivial. Since
$\alpha _0$ is trivial. Since ![]() $D(\cdot )$ is an anti-equivalence, we have thus shown that
$D(\cdot )$ is an anti-equivalence, we have thus shown that ![]() $\mathrm {Pic}^1$ has a rational point if and only if
$\mathrm {Pic}^1$ has a rational point if and only if ![]() $\alpha _0$ is trivial.
$\alpha _0$ is trivial.
To extend this to ![]() $\mathrm {Pic}^{d_0}$ and
$\mathrm {Pic}^{d_0}$ and ![]() $\alpha _0^{d_0}$, we note that their associated short exact sequences are given by the
$\alpha _0^{d_0}$, we note that their associated short exact sequences are given by the ![]() $d_0$-fold Baer sum [Sta, 010I] of (4.3.5) and (4.3.6), respectively. By definition,
$d_0$-fold Baer sum [Sta, 010I] of (4.3.5) and (4.3.6), respectively. By definition, ![]() $D(\cdot )$ commutes with direct sums and exchanges the addition map with the diagonal, i.e. for every
$D(\cdot )$ commutes with direct sums and exchanges the addition map with the diagonal, i.e. for every ![]() $G \in \mathrm {DCGS}_F$
$G \in \mathrm {DCGS}_F$
and, hence, also commutes with Baer sums. We thus deduce that ![]() $\mathrm {Pic}^{d_0}$ has a rational point if and only if
$\mathrm {Pic}^{d_0}$ has a rational point if and only if ![]() $\alpha _0^{d_0}$ is trivial, which proves the proposition.
$\alpha _0^{d_0}$ is trivial, which proves the proposition.
5. Main theorem
We are now ready to state and prove our main theorem. Let ![]() $S \to \mathsf {Spec}({\mathcal {O}})$ be either a smooth projective del Pezzo surface or a K3 surface satisfying Assumption 3.2.1 and consider the analytic manifold
$S \to \mathsf {Spec}({\mathcal {O}})$ be either a smooth projective del Pezzo surface or a K3 surface satisfying Assumption 3.2.1 and consider the analytic manifold ![]() $\operatorname {M}_{\beta,\chi }^\natural$ together with its canonical measure
$\operatorname {M}_{\beta,\chi }^\natural$ together with its canonical measure ![]() $\mu =\mu _{\rm can}$ as constructed in § 3.2.
$\mu =\mu _{\rm can}$ as constructed in § 3.2.
The restriction of the natural ![]() ${\mathbb {G}}_m$ gerbe
${\mathbb {G}}_m$ gerbe ![]() $\alpha \colon {\mathbb {M}}^{st}_{\beta,\chi } \to {\mathcal {M}}^{st}_{\beta,\chi }\cong \operatorname {M}^{st}_{\beta,\chi }$ induces a function
$\alpha \colon {\mathbb {M}}^{st}_{\beta,\chi } \to {\mathcal {M}}^{st}_{\beta,\chi }\cong \operatorname {M}^{st}_{\beta,\chi }$ induces a function
by pullback to the generic fiber as defined in (4.1.1).
Now for any ![]() $x \in \operatorname {M}_{\beta,\chi }(k)$ denote by
$x \in \operatorname {M}_{\beta,\chi }(k)$ denote by ![]() $\operatorname {M}_{\beta,\chi }({\mathcal {O}})_x \subset \operatorname {M}_{\beta,\chi }({\mathcal {O}})^\natural$ the ball of
$\operatorname {M}_{\beta,\chi }({\mathcal {O}})_x \subset \operatorname {M}_{\beta,\chi }({\mathcal {O}})^\natural$ the ball of ![]() ${\mathcal {O}}$-rational points specializing to
${\mathcal {O}}$-rational points specializing to ![]() $x$ over
$x$ over ![]() $k$. Then define the non-archimedean BPS function
$k$. Then define the non-archimedean BPS function ![]() $p\mathrm {BPS}_{\beta,\chi }:\operatorname {M}_{\beta,\chi }(k) \rightarrow {\mathbb {C}}$ to be
$p\mathrm {BPS}_{\beta,\chi }:\operatorname {M}_{\beta,\chi }(k) \rightarrow {\mathbb {C}}$ to be
Theorem 5.0.2 The function ![]() $p\mathrm {BPS}_{\beta,\chi }: \operatorname {M}_{\beta,\chi }(k) \rightarrow {\mathbb {C}}$ satisfies the following two properties:
$p\mathrm {BPS}_{\beta,\chi }: \operatorname {M}_{\beta,\chi }(k) \rightarrow {\mathbb {C}}$ satisfies the following two properties:
(i)
 $p\mathrm {BPS}_{\beta,\chi } \equiv q^{-\dim \operatorname {M}_{\beta,\chi }}$ if
$p\mathrm {BPS}_{\beta,\chi } \equiv q^{-\dim \operatorname {M}_{\beta,\chi }}$ if  $(\beta,\chi )$ is generic;Footnote 4
$(\beta,\chi )$ is generic;Footnote 4(ii) for all
 $\chi,\chi '\in \mathbb {Z}$ and for all
$\chi,\chi '\in \mathbb {Z}$ and for all  $y\in B(k)$ we have
$y\in B(k)$ we have
 \[ \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\sum _{x\in h_{\chi'}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi'}(x). \]
\[ \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\sum _{x\in h_{\chi'}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi'}(x). \]
Note that, by definition,
 \[ \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\int_{h_\chi^{-1}(B({\mathcal{O}})_y)} \varphi_{\beta,\chi}^g \, {\rm d}\mu. \]
\[ \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\int_{h_\chi^{-1}(B({\mathcal{O}})_y)} \varphi_{\beta,\chi}^g \, {\rm d}\mu. \]
To prove Theorem 5.0.2 we want to split up the integral using Fubini's theorem.
First let ![]() $B^{sm} \subset B$ be the open subscheme, where the universal curve
$B^{sm} \subset B$ be the open subscheme, where the universal curve ![]() ${\mathcal {C}} \rightarrow B$ is smooth. Then
${\mathcal {C}} \rightarrow B$ is smooth. Then ![]() $h_\chi ^{-1}( B({\mathcal {O}})_y\cap B^{sm}(F))$ is contained in
$h_\chi ^{-1}( B({\mathcal {O}})_y\cap B^{sm}(F))$ is contained in ![]() $h_\chi ^{-1}(B({\mathcal {O}})_y)$ and its complement has measure
$h_\chi ^{-1}(B({\mathcal {O}})_y)$ and its complement has measure ![]() $0$, since it is contained in
$0$, since it is contained in ![]() $h_\chi ^{-1}((B\setminus B^{sm})(F))$, that is, the
$h_\chi ^{-1}((B\setminus B^{sm})(F))$, that is, the ![]() $F$-points of a closed subscheme of
$F$-points of a closed subscheme of ![]() $\operatorname {M}_{\beta,\chi }$ (see [Reference Groechenig, Wyss and ZieglerGWZ20b, Proposition 4.4]).
$\operatorname {M}_{\beta,\chi }$ (see [Reference Groechenig, Wyss and ZieglerGWZ20b, Proposition 4.4]).
Since ![]() $h_\chi$ is proper, we can identify the fiber over a point
$h_\chi$ is proper, we can identify the fiber over a point ![]() $b \in B({\mathcal {O}}) \cap B^{sm}(F)$ with
$b \in B({\mathcal {O}}) \cap B^{sm}(F)$ with ![]() $h_\chi ^{-1}(b)(F)$ where we write
$h_\chi ^{-1}(b)(F)$ where we write ![]() $h_\chi ^{-1}(b)$ for the
$h_\chi ^{-1}(b)$ for the ![]() $F$-scheme
$F$-scheme ![]() $h_\chi ^{-1}(b)_F$. As in [Reference Groechenig, Wyss and ZieglerGWZ20b, § 6.3] we therefore have an equality:
$h_\chi ^{-1}(b)_F$. As in [Reference Groechenig, Wyss and ZieglerGWZ20b, § 6.3] we therefore have an equality:
 \begin{align} \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\int_{h_\chi^{-1}(B({\mathcal{O}})_y)} \varphi_{\beta,\chi}^g \,{\rm d}\mu = \int_{b\in B({\mathcal{O}})_y\cap B^{sm}(F)}\bigg(\int_{h_\chi^{-1}(b)(F)} \varphi_{\beta,\chi}^g \,{\rm d}\mu_{\omega_b}\bigg)\,{\rm d}\mu_{{\rm can},B}. \end{align}
\begin{align} \sum _{x\in h_{\chi}^{-1}(y)(k)} p\mathrm{BPS}_{\beta,\chi}(x)=\int_{h_\chi^{-1}(B({\mathcal{O}})_y)} \varphi_{\beta,\chi}^g \,{\rm d}\mu = \int_{b\in B({\mathcal{O}})_y\cap B^{sm}(F)}\bigg(\int_{h_\chi^{-1}(b)(F)} \varphi_{\beta,\chi}^g \,{\rm d}\mu_{\omega_b}\bigg)\,{\rm d}\mu_{{\rm can},B}. \end{align} Here ![]() $\omega _b$ is the gauge form on the
$\omega _b$ is the gauge form on the ![]() $\mathrm {Pic}^0_{{\mathcal {C}}_b}$-torsor
$\mathrm {Pic}^0_{{\mathcal {C}}_b}$-torsor ![]() $h_\chi ^{-1}(b) = \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$ from Lemma 3.2.3. As the outer integral in (5.0.3) is independent of
$h_\chi ^{-1}(b) = \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$ from Lemma 3.2.3. As the outer integral in (5.0.3) is independent of ![]() $\chi$ we only need to analyze the fiber integral
$\chi$ we only need to analyze the fiber integral ![]() $\int _{h_\chi ^{-1}(b)(F)}\varphi _{\beta,\chi }^g \,{\rm d}\mu _{\omega _b}$.
$\int _{h_\chi ^{-1}(b)(F)}\varphi _{\beta,\chi }^g \,{\rm d}\mu _{\omega _b}$.
First we note that the gerbe ![]() $\alpha \colon {\mathbb {M}}^{st}_{\beta,\chi } \rightarrow {\mathcal {M}}^{st}_{\beta,\chi }$ restricted to the fiber over
$\alpha \colon {\mathbb {M}}^{st}_{\beta,\chi } \rightarrow {\mathcal {M}}^{st}_{\beta,\chi }$ restricted to the fiber over ![]() $b$ gets identified with
$b$ gets identified with ![]() $\mathfrak {Pic}^{\chi +g-1}_{{\mathcal {C}}_b} \rightarrow \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$. Therefore, the associated function
$\mathfrak {Pic}^{\chi +g-1}_{{\mathcal {C}}_b} \rightarrow \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$. Therefore, the associated function ![]() $\varphi _{\beta,\chi }$ gets identified with
$\varphi _{\beta,\chi }$ gets identified with
where ![]() $f_{\chi +g-1}$ is the degree
$f_{\chi +g-1}$ is the degree ![]() $d=\chi +g-1$ component of the function
$d=\chi +g-1$ component of the function ![]() $f$ introduced in § 4.3. We may rewrite the innermost integral in (5.0.3) as
$f$ introduced in § 4.3. We may rewrite the innermost integral in (5.0.3) as
 \begin{equation} \int_{h_\chi^{-1}(b)(F)}\varphi_{\beta,\chi}^g \,{\rm d}\mu_{\omega_b} = \int_{\mathrm{Pic}^{\chi+g-1}_{{\mathcal{C}}_b}(F)} \varphi_{\chi+g-1}^g \,{\rm d}\mu_{\omega_b}. \end{equation}
\begin{equation} \int_{h_\chi^{-1}(b)(F)}\varphi_{\beta,\chi}^g \,{\rm d}\mu_{\omega_b} = \int_{\mathrm{Pic}^{\chi+g-1}_{{\mathcal{C}}_b}(F)} \varphi_{\chi+g-1}^g \,{\rm d}\mu_{\omega_b}. \end{equation} Now if ![]() $\mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}(F) = \emptyset$ this integral vanishes as we integrate over the empty manifold. Otherwise any
$\mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}(F) = \emptyset$ this integral vanishes as we integrate over the empty manifold. Otherwise any ![]() $x \in \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}(F)$ gives an isomorphism
$x \in \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}(F)$ gives an isomorphism ![]() $\mathrm {Pic}^{0}_{{\mathcal {C}}_b} \xrightarrow {\sim } \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$ and by (4.3.1) we have
$\mathrm {Pic}^{0}_{{\mathcal {C}}_b} \xrightarrow {\sim } \mathrm {Pic}^{\chi +g-1}_{{\mathcal {C}}_b}$ and by (4.3.1) we have
 \begin{equation} \int_{h^{-1}(b)(F)}\varphi_{\beta,\chi}^g \,{\rm d}\mu_{\omega_b} = \varphi_{\chi+g-1}^g(x) \int_{\mathrm{Pic}^0_{{\mathcal{C}}_b}(F)}\varphi_{0}^g \,{\rm d}\mu_{\omega_b} \end{equation}
\begin{equation} \int_{h^{-1}(b)(F)}\varphi_{\beta,\chi}^g \,{\rm d}\mu_{\omega_b} = \varphi_{\chi+g-1}^g(x) \int_{\mathrm{Pic}^0_{{\mathcal{C}}_b}(F)}\varphi_{0}^g \,{\rm d}\mu_{\omega_b} \end{equation} To complete the proof we need to further study the function ![]() $f_0: \mathrm {Pic}^0_{{\mathcal {C}}_b}(F) \rightarrow {\mathbb {Q}}/{\mathbb {Z}}$.
$f_0: \mathrm {Pic}^0_{{\mathcal {C}}_b}(F) \rightarrow {\mathbb {Q}}/{\mathbb {Z}}$.
Lemma 5.0.6 The following are equivalent:
(i)
 $f_0 \equiv 0$;
$f_0 \equiv 0$;(ii)
 $\mathrm {Pic}^1_{{\mathcal {C}}_b}(F)$ is non-empty;
$\mathrm {Pic}^1_{{\mathcal {C}}_b}(F)$ is non-empty;(iii)
 $\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)$ is non-empty.
$\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)$ is non-empty.
In this case the image of ![]() $f: \mathrm {Pic}_{{\mathcal {C}}_b}(F) \rightarrow {\mathbb {Q}}/{\mathbb {Z}}$ is contained in
$f: \mathrm {Pic}_{{\mathcal {C}}_b}(F) \rightarrow {\mathbb {Q}}/{\mathbb {Z}}$ is contained in ![]() $(({1}/{g}) {\mathbb {Z}})/{\mathbb {Z}}$.
$(({1}/{g}) {\mathbb {Z}})/{\mathbb {Z}}$.
Proof. The equivalence ![]() $\rm (i) \iff (ii)$ follows from Proposition 4.3.2. Clearly part (ii) implies part (iii) so we only need to prove that part (iii) implies part (i). Suppose then that
$\rm (i) \iff (ii)$ follows from Proposition 4.3.2. Clearly part (ii) implies part (iii) so we only need to prove that part (iii) implies part (i). Suppose then that ![]() $\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)$ is non-empty. We claim that
$\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)$ is non-empty. We claim that ![]() $f(\mathrm {Pic}^g_{{\mathcal {C}}_b}(F))=0$, where
$f(\mathrm {Pic}^g_{{\mathcal {C}}_b}(F))=0$, where
is as in § 4.3. Consider the moduli stack ![]() ${\mathbb {M}}_{\beta,1}$ of semi-stable sheaves with Euler characteristic
${\mathbb {M}}_{\beta,1}$ of semi-stable sheaves with Euler characteristic ![]() $\chi =1$. For this choice of
$\chi =1$. For this choice of ![]() $\chi$ there are no strictly semi-stable sheaves; hence every semi-stable sheaf is geometrically stable and, in particular, simple. It follows that the coarse space
$\chi$ there are no strictly semi-stable sheaves; hence every semi-stable sheaf is geometrically stable and, in particular, simple. It follows that the coarse space ![]() $M_{\beta,1}$ coincides with the
$M_{\beta,1}$ coincides with the ![]() ${\mathbb {G}}_m$-rigidification
${\mathbb {G}}_m$-rigidification ![]() ${\mathcal {M}}_{\beta,1}$, hence the coarse moduli map
${\mathcal {M}}_{\beta,1}$, hence the coarse moduli map ![]() ${\mathbb {M}}_{\beta,1}\to \operatorname {M}_{\beta,1}$ gives a
${\mathbb {M}}_{\beta,1}\to \operatorname {M}_{\beta,1}$ gives a ![]() ${\mathbb {G}}_m$ gerbe
${\mathbb {G}}_m$ gerbe ![]() $\alpha$ over
$\alpha$ over ![]() $\mathsf {Spec} \mathcal {O}$. For every
$\mathsf {Spec} \mathcal {O}$. For every ![]() $x\in \operatorname {M}_{\beta,1}(\mathcal {O})$, the pullback
$x\in \operatorname {M}_{\beta,1}(\mathcal {O})$, the pullback ![]() $x^*\alpha$ is a trivial gerbe, since
$x^*\alpha$ is a trivial gerbe, since ![]() $Br(\mathcal {O})=0$. In particular, the map
$Br(\mathcal {O})=0$. In particular, the map
vanishes. Now note that line bundles of degree ![]() $g$ have Euler characteristic
$g$ have Euler characteristic ![]() $1$, i.e.
$1$, i.e. ![]() $\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)\subset \operatorname {M}_{\beta,1}({\mathcal {O}})$. This proves the claim. To conclude the proof, let
$\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)\subset \operatorname {M}_{\beta,1}({\mathcal {O}})$. This proves the claim. To conclude the proof, let ![]() $x\in \mathrm {Pic}^g_{{\mathcal {C}}_b}(F)$. For every
$x\in \mathrm {Pic}^g_{{\mathcal {C}}_b}(F)$. For every ![]() $y\in Pic^0_{{\mathcal {C}}_b}(F)$,
$y\in Pic^0_{{\mathcal {C}}_b}(F)$, ![]() $f(y)=f(x)+f(y)=f(x+y)\in f(\mathrm {Pic}^g(F))=0$. Hence,
$f(y)=f(x)+f(y)=f(x+y)\in f(\mathrm {Pic}^g(F))=0$. Hence, ![]() $f_0$ is zero.
$f_0$ is zero.
The statement about the image of ![]() $f$ follows from the observation
$f$ follows from the observation ![]() $f(\mathrm {Pic}_{{\mathcal {C}}_b}^g(F))=0$.
$f(\mathrm {Pic}_{{\mathcal {C}}_b}^g(F))=0$.
Remark 5.0.7 The equivalence of parts (ii) and (iii) in Lemma 5.0.6 is true more generally. In fact, for any geometrically integral, smooth projective curve ![]() $C$ of genus
$C$ of genus ![]() $g$ over a local field
$g$ over a local field ![]() $\mathrm {Pic}_C^{g-1}$ has a rational point by [Reference LichtenbaumLic69] and [Reference Poonen and StollPS99, Corollary 4].
$\mathrm {Pic}_C^{g-1}$ has a rational point by [Reference LichtenbaumLic69] and [Reference Poonen and StollPS99, Corollary 4].
Proof of Theorem 5.0.2 By the previous discussion, in particular (5.0.3) and (5.0.4), ![]() $\chi$ independence amounts to show for all
$\chi$ independence amounts to show for all ![]() $d,d' \in {\mathbb {Z}}$ and
$d,d' \in {\mathbb {Z}}$ and ![]() $b \in B({\mathcal {O}}) \cap B^{sm}(F)$ the equality
$b \in B({\mathcal {O}}) \cap B^{sm}(F)$ the equality
 \[ \int_{\mathrm{Pic}^{d}_{{\mathcal{C}}_b}(F)}\varphi_{d}^g \,{\rm d}\mu_{\omega_b} = \int_{\mathrm{Pic}^{d'}_{{\mathcal{C}}_b}(F)} \varphi_{d'}^g \,{\rm d}\mu_{\omega_b}. \]
\[ \int_{\mathrm{Pic}^{d}_{{\mathcal{C}}_b}(F)}\varphi_{d}^g \,{\rm d}\mu_{\omega_b} = \int_{\mathrm{Pic}^{d'}_{{\mathcal{C}}_b}(F)} \varphi_{d'}^g \,{\rm d}\mu_{\omega_b}. \]
For simplicity take ![]() $d' = g$. Consider first the case where
$d' = g$. Consider first the case where ![]() $\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)=\emptyset$. Then the right-hand side is zero. If
$\mathrm {Pic}^g_{{\mathcal {C}}_b}(F)=\emptyset$. Then the right-hand side is zero. If ![]() $\mathrm {Pic}^d_{{\mathcal {C}}_b}(F)$ is also empty, we are done. Otherwise, let
$\mathrm {Pic}^d_{{\mathcal {C}}_b}(F)$ is also empty, we are done. Otherwise, let ![]() $x\in \mathrm {Pic}^d(F)$. Then as in (5.0.5)
$x\in \mathrm {Pic}^d(F)$. Then as in (5.0.5)
 \begin{equation} \int_{\mathrm{Pic}^{d}_{{\mathcal{C}}_b}(F)}\varphi_{d}^g \,{\rm d}\mu_{\omega_b} = \varphi_{d}^g(x) \int_{\mathrm{Pic}^0_{{\mathcal{C}}_b}(F)}\varphi_{0}^g \,{\rm d}\mu_{\omega_b}. \end{equation}
\begin{equation} \int_{\mathrm{Pic}^{d}_{{\mathcal{C}}_b}(F)}\varphi_{d}^g \,{\rm d}\mu_{\omega_b} = \varphi_{d}^g(x) \int_{\mathrm{Pic}^0_{{\mathcal{C}}_b}(F)}\varphi_{0}^g \,{\rm d}\mu_{\omega_b}. \end{equation} As ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^g(F)$ is empty, so is
$\mathrm {Pic}_{{\mathcal {C}}_b}^g(F)$ is empty, so is ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^1(F)$ by Lemma 5.0.6, hence
$\mathrm {Pic}_{{\mathcal {C}}_b}^1(F)$ by Lemma 5.0.6, hence ![]() $f_0$ is a non-trivial character, i.e. a surjective homomorphism
$f_0$ is a non-trivial character, i.e. a surjective homomorphism ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^0(F)\to {\mathbb {Z}}/d_0{\mathbb {Z}}$ for some
$\mathrm {Pic}_{{\mathcal {C}}_b}^0(F)\to {\mathbb {Z}}/d_0{\mathbb {Z}}$ for some ![]() $d_0\geq 2$ by Lemma 4.3.2. Furthermore,
$d_0\geq 2$ by Lemma 4.3.2. Furthermore, ![]() $d_0$ is the smallest integer such that
$d_0$ is the smallest integer such that ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^{d_0}(F)\neq \emptyset$, hence
$\mathrm {Pic}_{{\mathcal {C}}_b}^{d_0}(F)\neq \emptyset$, hence ![]() $d_0$ does not divide
$d_0$ does not divide ![]() $g$. The function
$g$. The function ![]() $\varphi _0^g$ is therefore non-zero and by a character-sum argument the right-hand side of (5.0.8) vanishes, as required.
$\varphi _0^g$ is therefore non-zero and by a character-sum argument the right-hand side of (5.0.8) vanishes, as required.
Next we consider the case ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^g(F)\neq \emptyset$. Then by Lemma 5.0.6 also
$\mathrm {Pic}_{{\mathcal {C}}_b}^g(F)\neq \emptyset$. Then by Lemma 5.0.6 also ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^1(F)\neq \emptyset$ and, thus, also
$\mathrm {Pic}_{{\mathcal {C}}_b}^1(F)\neq \emptyset$ and, thus, also ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^d(F)\neq \emptyset$. Furthermore, the image of
$\mathrm {Pic}_{{\mathcal {C}}_b}^d(F)\neq \emptyset$. Furthermore, the image of ![]() $f$ is
$f$ is ![]() $g$-torsion and, thus,
$g$-torsion and, thus, ![]() $\varphi _d^g=\varphi _g^g \equiv 1$. Since
$\varphi _d^g=\varphi _g^g \equiv 1$. Since ![]() $\mathrm {Pic}_{{\mathcal {C}}_b}^d(F) \cong \mathrm {Pic}_{{\mathcal {C}}_b}^0(F) \cong \mathrm {Pic}_{{\mathcal {C}}_b}^g(F)$ we are done with the proof of part (ii).
$\mathrm {Pic}_{{\mathcal {C}}_b}^d(F) \cong \mathrm {Pic}_{{\mathcal {C}}_b}^0(F) \cong \mathrm {Pic}_{{\mathcal {C}}_b}^g(F)$ we are done with the proof of part (ii).
The proof of part (i) follows from the fact that for ![]() $(\beta,\chi )$ generic, the stable locus is everything, thus the morphism
$(\beta,\chi )$ generic, the stable locus is everything, thus the morphism ![]() ${\mathbb {M}}_{\beta,\chi } \to \operatorname {M}_{\beta,\chi }$ is a
${\mathbb {M}}_{\beta,\chi } \to \operatorname {M}_{\beta,\chi }$ is a ![]() ${\mathbb {G}}_m$ gerbe. In this case
${\mathbb {G}}_m$ gerbe. In this case ![]() $f_{\beta,\chi } \equiv 0$, since the gerbe
$f_{\beta,\chi } \equiv 0$, since the gerbe ![]() $x^*\alpha \in H^2(F,{\mathbb {G}}_m)$ is pulled back from
$x^*\alpha \in H^2(F,{\mathbb {G}}_m)$ is pulled back from ![]() $H^2(\mathsf {Spec}({\mathcal {O}}),{\mathbb {G}}_m) = 0$ and, thus, trivial.
$H^2(\mathsf {Spec}({\mathcal {O}}),{\mathbb {G}}_m) = 0$ and, thus, trivial.
Acknowledgements
We warmly thank Michael Groechenig and Paul Ziegler for numerous discussions, which were at the origin of many ideas in this paper. We also would like to thank Ben Davison, Pierrick Bousseau, Sven Meinhardt and Tanguy Vernet for interesting conversations around ![]() $\mathrm {BPS}$ invariants. We also thank the anonymous referee, whose comments greatly improved the exposition. This work was supported by the Swiss National Science Foundation [No. 196960].
$\mathrm {BPS}$ invariants. We also thank the anonymous referee, whose comments greatly improved the exposition. This work was supported by the Swiss National Science Foundation [No. 196960].
Conflicts of Interest
None.