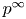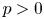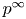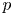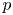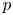1. Introduction
In this article we want to study problems related to the finiteness of the ![]() $p$-primary torsion of the Brauer group of abelian varieties in positive characteristic
$p$-primary torsion of the Brauer group of abelian varieties in positive characteristic ![]() $p$. If
$p$. If ![]() $k$ is a finite field and
$k$ is a finite field and ![]() $A$ is an abelian variety over
$A$ is an abelian variety over ![]() $k$, it is well-known that the Brauer group of
$k$, it is well-known that the Brauer group of ![]() $A$, defined as
$A$, defined as ![]() $\mathrm {Br}(A):=H^2_\mathrm {\acute {e}t}(A,\mathbb {G}_m)$, is a finite group [Reference TateTat94, Proposition 4.3]. The main input for this result is the Tate conjecture for divisors, proved by Tate in [Reference TateTat66]. If
$\mathrm {Br}(A):=H^2_\mathrm {\acute {e}t}(A,\mathbb {G}_m)$, is a finite group [Reference TateTat94, Proposition 4.3]. The main input for this result is the Tate conjecture for divisors, proved by Tate in [Reference TateTat66]. If ![]() $k$ is replaced by a finitely generated field extension of
$k$ is replaced by a finitely generated field extension of ![]() $\mathbb {F}_p$ one can no longer expect
$\mathbb {F}_p$ one can no longer expect ![]() $\mathrm {Br}(A)$ to be finite (see [Reference Skorobogatov and ZarhinSZ08, § 1]). On the other hand, if
$\mathrm {Br}(A)$ to be finite (see [Reference Skorobogatov and ZarhinSZ08, § 1]). On the other hand, if ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}$ is the transcendental Brauer group of
$\mathrm {Br}(A_{{k_s}}\!)^{k}$ is the transcendental Brauer group of ![]() $A$, namely the image of
$A$, namely the image of ![]() $\mathrm {Br}(A)\to \mathrm {Br}(A_{{k_s}}\!)$ where
$\mathrm {Br}(A)\to \mathrm {Br}(A_{{k_s}}\!)$ where ![]() ${k_s}$ is a separable closure of
${k_s}$ is a separable closure of ![]() $k$, the group
$k$, the group ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}[\frac {1}{p}]$ is finite by [Reference Colliot-Thélène and SkorobogatovCS21, Theorem 16.2.3]. In [Reference Skorobogatov and ZarhinSZ08, Question 1], Skorobogatov and Zarhin asked whether the
$\mathrm {Br}(A_{{k_s}}\!)^{k}[\frac {1}{p}]$ is finite by [Reference Colliot-Thélène and SkorobogatovCS21, Theorem 16.2.3]. In [Reference Skorobogatov and ZarhinSZ08, Question 1], Skorobogatov and Zarhin asked whether the ![]() $p$-primary torsion of
$p$-primary torsion of ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}$ is also finite. This question has a negative answer already for abelian surfaces, as we show in Proposition 5.4. Nonetheless, we prove the following alternative finiteness result. Write
$\mathrm {Br}(A_{{k_s}}\!)^{k}$ is also finite. This question has a negative answer already for abelian surfaces, as we show in Proposition 5.4. Nonetheless, we prove the following alternative finiteness result. Write ![]() ${\bar {k}}$ for an algebraic closure of
${\bar {k}}$ for an algebraic closure of ![]() $k_s$.
$k_s$.
Theorem 1.1 (Theorem 5.2)
Let ![]() $A$ be an abelian variety over a finitely generated field
$A$ be an abelian variety over a finitely generated field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$. The transcendental Brauer group
$p>0$. The transcendental Brauer group ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}$ is a direct sum of a finite group and a finite exponent
$\mathrm {Br}(A_{{k_s}}\!)^{k}$ is a direct sum of a finite group and a finite exponent ![]() $p$-group. In addition, if the Witt vector cohomology group
$p$-group. In addition, if the Witt vector cohomology group ![]() $H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite
$H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite ![]() $W({\bar {k}})$-module, then
$W({\bar {k}})$-module, then ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}$ is finite.
$\mathrm {Br}(A_{{k_s}}\!)^{k}$ is finite.
The condition on ![]() $H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is necessary to remove the ‘supersingular pathologies’ as the one of our counterexample and it is satisfied, for example, when the
$H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is necessary to remove the ‘supersingular pathologies’ as the one of our counterexample and it is satisfied, for example, when the ![]() $p$-rank of
$p$-rank of ![]() $A$ is
$A$ is ![]() $g$ or
$g$ or ![]() $g-1$, where
$g-1$, where ![]() $g$ is the dimension of
$g$ is the dimension of ![]() $A$ (see [Reference IllusieIll83, Corollary 6.3.16]). Note that if the formal Brauer group of
$A$ (see [Reference IllusieIll83, Corollary 6.3.16]). Note that if the formal Brauer group of ![]() $A_{\bar {k}}$, denoted by
$A_{\bar {k}}$, denoted by ![]() $\hat {\mathrm {Br}}(A_{\bar {k}})$, is a formal Lie group, then by [Reference Artin and MazurAM77, Corollary II.4.4] the cohomology group
$\hat {\mathrm {Br}}(A_{\bar {k}})$, is a formal Lie group, then by [Reference Artin and MazurAM77, Corollary II.4.4] the cohomology group ![]() $H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite
$H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite ![]() $W({\bar {k}})$-module if and only if
$W({\bar {k}})$-module if and only if ![]() $\hat {\mathrm {Br}}(A_{\bar {k}})$ has finite height. Note also that the formal Brauer group of abelian surfaces is always a formal Lie group by [Reference Artin and MazurAM77, Corollary II.2.12]. As a consequence of Theorem 1.1, we deduce that the subgroup of Galois-fixed points of
$\hat {\mathrm {Br}}(A_{\bar {k}})$ has finite height. Note also that the formal Brauer group of abelian surfaces is always a formal Lie group by [Reference Artin and MazurAM77, Corollary II.2.12]. As a consequence of Theorem 1.1, we deduce that the subgroup of Galois-fixed points of ![]() $\mathrm {Br}(A_{{k_s}}\!)$, denoted by
$\mathrm {Br}(A_{{k_s}}\!)$, denoted by ![]() $\mathrm {Br}(A_{{k_s}}\!)^{\Gamma _k}$, has finite exponent (Corollary 5.3). This is a variant of [Reference Skorobogatov and ZarhinSZ08, Question 2] for abelian varieties.
$\mathrm {Br}(A_{{k_s}}\!)^{\Gamma _k}$, has finite exponent (Corollary 5.3). This is a variant of [Reference Skorobogatov and ZarhinSZ08, Question 2] for abelian varieties.
In this article, we also study the Galois-fixed points of ![]() $\mathrm {Br}(A_{{\bar {k}}})$. Ulmer in [Reference UlmerUlm14, § 7.3.1] conjectured that
$\mathrm {Br}(A_{{\bar {k}}})$. Ulmer in [Reference UlmerUlm14, § 7.3.1] conjectured that ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}=0$ where
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}=0$ where ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ is the
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ is the ![]() $p$-adic Tate module of
$p$-adic Tate module of ![]() $\mathrm {Br}(A_{{\bar {k}}})$. Even in this case, we provide a counterexample to this conjecture. We use the following result.
$\mathrm {Br}(A_{{\bar {k}}})$. Even in this case, we provide a counterexample to this conjecture. We use the following result.
Proposition 1.2 (Proposition 6.6)
Let ![]() $B$ be an abelian variety over a finitely generated field
$B$ be an abelian variety over a finitely generated field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$. Write
$p>0$. Write ![]() $A$ for
$A$ for ![]() $B\times _k B$ and
$B\times _k B$ and ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ for the
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ for the ![]() $p$-adic Tate module of
$p$-adic Tate module of ![]() $\mathrm {Br}(A_{\bar {k}})$. There is a natural exact sequence
$\mathrm {Br}(A_{\bar {k}})$. There is a natural exact sequence
where ![]() $\operatorname {Hom}(B,B^\vee )$ denotes the group of homomorphisms
$\operatorname {Hom}(B,B^\vee )$ denotes the group of homomorphisms ![]() $B\to B^\vee$ as abelian varieties over
$B\to B^\vee$ as abelian varieties over ![]() $k$.
$k$.
The proposition implies, for example, that when ![]() $\operatorname {End}(B)=\mathbb {Z}$ the
$\operatorname {End}(B)=\mathbb {Z}$ the ![]() $\Gamma _k$-module
$\Gamma _k$-module ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ admits non-zero Galois-fixed points (Corollary 6.7). In this case,
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ admits non-zero Galois-fixed points (Corollary 6.7). In this case, ![]() $\mathrm {Br}(A_{{\bar {k}}})^{\Gamma _k}$ has infinite exponent since
$\mathrm {Br}(A_{{\bar {k}}})^{\Gamma _k}$ has infinite exponent since
Note that if we replace ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ with the
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ with the ![]() $\ell$-adic Tate module
$\ell$-adic Tate module ![]() $\mathrm {T_\ell }(\mathrm {Br}(A_{\bar {k}}))$, where
$\mathrm {T_\ell }(\mathrm {Br}(A_{\bar {k}}))$, where ![]() $\ell$ is a prime different from
$\ell$ is a prime different from ![]() $p$, then
$p$, then ![]() $\mathrm {T_\ell }(\mathrm {Br}(A_{{k_s}}\!))=\mathrm {T_\ell }(\mathrm {Br}(A_{\bar {k}}))$ has no non-trivial Galois-fixed points.
$\mathrm {T_\ell }(\mathrm {Br}(A_{{k_s}}\!))=\mathrm {T_\ell }(\mathrm {Br}(A_{\bar {k}}))$ has no non-trivial Galois-fixed points.
These ‘exceptional classes’ in ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}$ are naturally related to specialisation morphisms of Néron–Severi groups. We recall the following theorem, which was proved in [Reference AndréAnd96, Theorem 5.2] in characteristic
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}$ are naturally related to specialisation morphisms of Néron–Severi groups. We recall the following theorem, which was proved in [Reference AndréAnd96, Theorem 5.2] in characteristic ![]() $0$ (see also [Reference Maulik and PoonenMP12]) and in [Reference AmbrosiAmb23] and [Reference ChristensenChr18] in positive characteristic.
$0$ (see also [Reference Maulik and PoonenMP12]) and in [Reference AmbrosiAmb23] and [Reference ChristensenChr18] in positive characteristic.
Theorem 1.3 (André, Ambrosi, Christensen)
Let ![]() $K$ be an algebraically closed field which is not an algebraic extension of a finite field,
$K$ be an algebraically closed field which is not an algebraic extension of a finite field, ![]() $X$ a finite-type
$X$ a finite-type ![]() $K$-scheme, and
$K$-scheme, and ![]() $\mathcal {Y}\to X$ a smooth proper morphism. For every geometric point
$\mathcal {Y}\to X$ a smooth proper morphism. For every geometric point ![]() $\bar {\eta }$ of
$\bar {\eta }$ of ![]() $X$ there is an
$X$ there is an ![]() $x\in X(K)$ such that
$x\in X(K)$ such that ![]() $\operatorname {rk}_\mathbb {Z}(\mathrm {NS}(\mathcal {Y}_{\bar {\eta }}))=\operatorname {rk}_\mathbb {Z}(\mathrm {NS}(\mathcal {Y}_x))$.Footnote 1
$\operatorname {rk}_\mathbb {Z}(\mathrm {NS}(\mathcal {Y}_{\bar {\eta }}))=\operatorname {rk}_\mathbb {Z}(\mathrm {NS}(\mathcal {Y}_x))$.Footnote 1
As it is well-known, the theorem is false when ![]() $K=\bar {\mathbb {F}}_p$ (see [Reference Maulik and PoonenMP12, Remark 1.12]). What we prove is that, in the known counterexamples, the elements in
$K=\bar {\mathbb {F}}_p$ (see [Reference Maulik and PoonenMP12, Remark 1.12]). What we prove is that, in the known counterexamples, the elements in ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}$ explain the failure of Theorem 1.3. More precisely, we prove the following result.
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}$ explain the failure of Theorem 1.3. More precisely, we prove the following result.
Theorem 1.4 (Theorem 6.2)
Let ![]() $X$ be a connected normal scheme of finite type over
$X$ be a connected normal scheme of finite type over ![]() $\mathbb {F}_p$ with generic point
$\mathbb {F}_p$ with generic point ![]() $\eta =\operatorname {Spec}(k)$ and let
$\eta =\operatorname {Spec}(k)$ and let ![]() $f:\mathcal {A}\to X$ be an abelian scheme over
$f:\mathcal {A}\to X$ be an abelian scheme over ![]() $X$ with constant Newton polygon.Footnote 2 For every closed point
$X$ with constant Newton polygon.Footnote 2 For every closed point ![]() $x=\operatorname {Spec}(\kappa )$ of
$x=\operatorname {Spec}(\kappa )$ of ![]() $X$ we have
$X$ we have
Note that in the inequality the left term is ‘motivic’, whereas the right term comes from some ![]() $p$-adic object which, as far as we know, has no
$p$-adic object which, as far as we know, has no ![]() $\ell$-adic analogue. Note also that
$\ell$-adic analogue. Note also that ![]() $\mathrm {T}_p(\mathrm {Br}(\mathcal {A}_{\bar {x}}))^{\Gamma _\kappa }=0$ by Corollary 5.3 since
$\mathrm {T}_p(\mathrm {Br}(\mathcal {A}_{\bar {x}}))^{\Gamma _\kappa }=0$ by Corollary 5.3 since ![]() $\kappa$ is a perfect field.
$\kappa$ is a perfect field.
To prove Theorem 1.1 we use a flat variant of the Tate conjecture. For every ![]() $n$, let
$n$, let ![]() $H^2_\mathrm {fppf}(A_{\bar {k}},{\mu _{p^n}}\!)^k$ be the image of the extension of scalars morphism
$H^2_\mathrm {fppf}(A_{\bar {k}},{\mu _{p^n}}\!)^k$ be the image of the extension of scalars morphism ![]() $H^2_\mathrm {fppf}(A,{\mu _{p^n}}\!)\to H^2_\mathrm {fppf}(A_{\bar {k}},{\mu _{p^n}}\!)$.
$H^2_\mathrm {fppf}(A,{\mu _{p^n}}\!)\to H^2_\mathrm {fppf}(A_{\bar {k}},{\mu _{p^n}}\!)$.
Theorem 1.5 (Theorem 5.1)
After possibly replacing ![]() $k$ with a finite separable extension, the cycle class map
$k$ with a finite separable extension, the cycle class map
becomes an isomorphism.Footnote 3
We obtain this result by using the crystalline Tate conjecture for abelian varieties, proved by de Jong in [Reference de JongdeJ98, Theorem 2.6]. The main issue that we have to overcome is the lack of a good comparison between crystalline and fppf cohomology of ![]() ${\mathbb {Z}_{p}}(1)$ over imperfect fields. To avoid this problem, we exploit the fact that we are working with abelian varieties. In this special case, the comparison is constructed using the
${\mathbb {Z}_{p}}(1)$ over imperfect fields. To avoid this problem, we exploit the fact that we are working with abelian varieties. In this special case, the comparison is constructed using the ![]() $p$-divisible group of
$p$-divisible group of ![]() $A$ (and its dual).
$A$ (and its dual).
The technical issue that we have to solve using the groups ![]() $H^2_{\mathrm {fppf}}(A_{\bar {k}},{\mu _{p^n}}\!)^k$ is that it is not clear a priori whether
$H^2_{\mathrm {fppf}}(A_{\bar {k}},{\mu _{p^n}}\!)^k$ is that it is not clear a priori whether ![]() $H^2_{\mathrm {fppf}}(A,{\mathbb {Z}_{p}}(1))\to \varprojlim _n H^2_{\mathrm {fppf}}(A_{\bar {k}},{\mu _{p^n}}\!)^k$ is surjective. This is done (after inverting
$H^2_{\mathrm {fppf}}(A,{\mathbb {Z}_{p}}(1))\to \varprojlim _n H^2_{\mathrm {fppf}}(A_{\bar {k}},{\mu _{p^n}}\!)^k$ is surjective. This is done (after inverting ![]() $p$) in Proposition 3.9, where we reduce to the case when
$p$) in Proposition 3.9, where we reduce to the case when ![]() $A$ is the Jacobian of a curve. This idea was inspired by the proof of [Reference Colliot-Thélène and SkorobogatovCS13, Theorem 2.1].
$A$ is the Jacobian of a curve. This idea was inspired by the proof of [Reference Colliot-Thélène and SkorobogatovCS13, Theorem 2.1].
1.6 Outline of the article
In § 3 we prove some general results on the cohomology of fppf sheaves. In particular, we prove Corollary 3.4, which is a first result on the relation between the Brauer group of a scheme over ![]() ${k_s}$ and
${k_s}$ and ![]() ${\bar {k}}$. In this section, we also prove in Proposition 3.8 the exactness of some fundamental sequences for the groups
${\bar {k}}$. In this section, we also prove in Proposition 3.8 the exactness of some fundamental sequences for the groups ![]() $H^2_\mathrm {fppf}(X_{\bar {k}},{\mu _{p^n}}\!)^k$. In § 4, we construct a morphism which relates
$H^2_\mathrm {fppf}(X_{\bar {k}},{\mu _{p^n}}\!)^k$. In § 4, we construct a morphism which relates ![]() $H^2_\mathrm {fppf}(A,{\mathbb {Z}_{p}}(1))$ with
$H^2_\mathrm {fppf}(A,{\mathbb {Z}_{p}}(1))$ with ![]() $\operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$ and we prove basic properties of this morphism as Propositions 4.5 and 4.6. In § 5, we prove the flat variant of the Tate conjecture (Theorem 5.1) and the finiteness result for the transcendental Brauer group (Theorem 5.2). Finally, in § 6, we look at the relation of our results with the theory of specialisation of Néron–Severi groups. In particular, we prove Theorem 6.2.
$\operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$ and we prove basic properties of this morphism as Propositions 4.5 and 4.6. In § 5, we prove the flat variant of the Tate conjecture (Theorem 5.1) and the finiteness result for the transcendental Brauer group (Theorem 5.2). Finally, in § 6, we look at the relation of our results with the theory of specialisation of Néron–Severi groups. In particular, we prove Theorem 6.2.
2. Notation
If ![]() $k$ is a field, we write
$k$ is a field, we write ![]() ${\bar {k}}$ for a fixed algebraic closure of
${\bar {k}}$ for a fixed algebraic closure of ![]() $k$ and
$k$ and ![]() ${k_s}$ (respectively,
${k_s}$ (respectively, ![]() ${k_i}$) for the separable (respectively, purely inseparable) closure of
${k_i}$) for the separable (respectively, purely inseparable) closure of ![]() $k$ in
$k$ in ![]() ${\bar {k}}$. We denote by
${\bar {k}}$. We denote by ![]() $\Gamma _k$ the absolute Galois group of
$\Gamma _k$ the absolute Galois group of ![]() $k$. If
$k$. If ![]() $x$ is a
$x$ is a ![]() $k$-point of a scheme, we denote by
$k$-point of a scheme, we denote by ![]() $\bar {x}$ the induced
$\bar {x}$ the induced ![]() ${\bar {k}}$-point. For an abelian group
${\bar {k}}$-point. For an abelian group ![]() $M$, we write
$M$, we write ![]() $\mathrm {T}_p(M)$ for the
$\mathrm {T}_p(M)$ for the ![]() $p$-adic Tate module of
$p$-adic Tate module of ![]() $M$, which is the projective limit
$M$, which is the projective limit ![]() $\varprojlim _{n}M[p^n]$, we write
$\varprojlim _{n}M[p^n]$, we write ![]() $\mathrm {V}_p(M)$ for
$\mathrm {V}_p(M)$ for ![]() $\mathrm {T}_p(M)[\frac {1}{p}]$, and we write
$\mathrm {T}_p(M)[\frac {1}{p}]$, and we write ![]() $M^\wedge$ for the
$M^\wedge$ for the ![]() $p$-adic completion of
$p$-adic completion of ![]() $M$. If
$M$. If ![]() $M$ is endowed with a
$M$ is endowed with a ![]() $\Gamma _k$-action, we denote by
$\Gamma _k$-action, we denote by ![]() $M^{\Gamma _k}$ the subgroup of fixed points. For a scheme
$M^{\Gamma _k}$ the subgroup of fixed points. For a scheme ![]() $X$ and an fppf sheaf
$X$ and an fppf sheaf ![]() $\mathcal {F}$, we denote by
$\mathcal {F}$, we denote by ![]() $H^{\bullet }(X,\mathcal {F})$ the fppf cohomology groups and when
$H^{\bullet }(X,\mathcal {F})$ the fppf cohomology groups and when ![]() $X=\operatorname {Spec}(k)$ we simply write
$X=\operatorname {Spec}(k)$ we simply write ![]() $H^{\bullet }(k,\mathcal {F})$. If
$H^{\bullet }(k,\mathcal {F})$. If ![]() $f:X\to Y$ is a morphism of schemes, we denote by
$f:X\to Y$ is a morphism of schemes, we denote by ![]() $R^{\bullet }f_*\mathcal {F}$ the fppf higher direct image functors over
$R^{\bullet }f_*\mathcal {F}$ the fppf higher direct image functors over ![]() $(\mathbf {Sch}/Y)_\mathrm {fppf}$. Finally, if
$(\mathbf {Sch}/Y)_\mathrm {fppf}$. Finally, if ![]() $X$ is a scheme over
$X$ is a scheme over ![]() $\mathbb {F}_p$, we write
$\mathbb {F}_p$, we write ![]() $X^{\mathrm {perf}}$ for the projective limit
$X^{\mathrm {perf}}$ for the projective limit ![]() $\varprojlim (\cdots \xrightarrow {F}X\xrightarrow {F}X\xrightarrow {F}X)$ where
$\varprojlim (\cdots \xrightarrow {F}X\xrightarrow {F}X\xrightarrow {F}X)$ where ![]() $F$ is the absolute Frobenius of
$F$ is the absolute Frobenius of ![]() $X$.
$X$.
3. Preliminary results
In this section we start by proving some results that we will use later on. We work over a field ![]() $k$ of arbitrary characteristic and we consider a scheme
$k$ of arbitrary characteristic and we consider a scheme ![]() $X$ over
$X$ over ![]() $k$ with structural morphism
$k$ with structural morphism ![]() $q$.
$q$.
Lemma 3.1 Let ![]() $\mathcal {F}$ be a sheaf over
$\mathcal {F}$ be a sheaf over ![]() $(\mathbf {Sch}/k)_\mathrm {fppf}$ such that
$(\mathbf {Sch}/k)_\mathrm {fppf}$ such that ![]() $q_*\mathcal {F}_{X}=\mathcal {F}$ and suppose that
$q_*\mathcal {F}_{X}=\mathcal {F}$ and suppose that ![]() $X$ has a
$X$ has a ![]() $k$-rational point. The group
$k$-rational point. The group ![]() $H^0(k,R^1q_*\mathcal {F}_{X}\!)$ is canonically isomorphic to
$H^0(k,R^1q_*\mathcal {F}_{X}\!)$ is canonically isomorphic to ![]() $H^1(X,\mathcal {F}_X\!)/H^1(k,\mathcal {F})$. In addition, the natural morphism
$H^1(X,\mathcal {F}_X\!)/H^1(k,\mathcal {F})$. In addition, the natural morphism ![]() $H^2(X,\mathcal {F}_X\!)\to H^0(k,R^2q_*\mathcal {F}_{X}\!)$ sits in an exact sequence
$H^2(X,\mathcal {F}_X\!)\to H^0(k,R^2q_*\mathcal {F}_{X}\!)$ sits in an exact sequence
where ![]() $K$ is an extension of
$K$ is an extension of ![]() $H^1(k,R^1q_*\mathcal {F}_{X}\!)$ by
$H^1(k,R^1q_*\mathcal {F}_{X}\!)$ by ![]() $H^2(k,\mathcal {F})$.
$H^2(k,\mathcal {F})$.
Proof. We consider the Leray spectral sequence
The morphisms ![]() $E^{i,0}_2=H^i(k,q_*\mathcal {F}_X\!)=H^i(k,\mathcal {F})\to H^i(X,\mathcal {F}_X\!)$ are injective since
$E^{i,0}_2=H^i(k,q_*\mathcal {F}_X\!)=H^i(k,\mathcal {F})\to H^i(X,\mathcal {F}_X\!)$ are injective since ![]() $X$ admits a
$X$ admits a ![]() $k$-rational point. We deduce that
$k$-rational point. We deduce that ![]() $E^{1,1}_2=E^{1,1}_\infty$ and
$E^{1,1}_2=E^{1,1}_\infty$ and ![]() $E^{2,0}_2=E^{2,0}_\infty$. This implies that the kernel of
$E^{2,0}_2=E^{2,0}_\infty$. This implies that the kernel of ![]() $H^2(X,\mathcal {F}_X\!)\to E^{0,2}_\infty$ is an extension of
$H^2(X,\mathcal {F}_X\!)\to E^{0,2}_\infty$ is an extension of ![]() $E^{1,1}_2$ by
$E^{1,1}_2$ by ![]() $E^{2,0}_2$, as we wanted. The obstruction for the map
$E^{2,0}_2$, as we wanted. The obstruction for the map ![]() $H^2(X,\mathcal {F}_X\!)\to E^{0,2}_2=H^0(k,R^2q_*\mathcal {F}_{X}\!)$ to be surjective lies in
$H^2(X,\mathcal {F}_X\!)\to E^{0,2}_2=H^0(k,R^2q_*\mathcal {F}_{X}\!)$ to be surjective lies in ![]() $E^{2,1}_2=H^2(k,R^1q_*\mathcal {F}_X\!)$. This concludes the proof.
$E^{2,1}_2=H^2(k,R^1q_*\mathcal {F}_X\!)$. This concludes the proof.
Definition 3.2 We say that a presheaf ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $(\mathbf {Sch}^{\mathrm {qcqs}}/k)_{\mathrm {fppf}}$ is finitary if for every inverse system
$(\mathbf {Sch}^{\mathrm {qcqs}}/k)_{\mathrm {fppf}}$ is finitary if for every inverse system ![]() $\{T^{(\ell )}\}_{\ell \in L}$ of quasi-compact quasi-separated
$\{T^{(\ell )}\}_{\ell \in L}$ of quasi-compact quasi-separated ![]() $k$-schemes with affine transition maps, the natural morphism
$k$-schemes with affine transition maps, the natural morphism
is an isomorphism.
Lemma 3.3 Let ![]() $G$ be a commutative finite-type group scheme over
$G$ be a commutative finite-type group scheme over ![]() $k$. If
$k$. If ![]() $X$ is quasi-compact quasi-separated, then
$X$ is quasi-compact quasi-separated, then ![]() $R^iq_*G_X$ is finitary for
$R^iq_*G_X$ is finitary for ![]() $i\geq 0$. In addition, the natural morphism
$i\geq 0$. In addition, the natural morphism ![]() $H^0(k,R^i q_*G_X\!)\to H^{i}(X_{\bar {k}},G_{X_{\bar {k}}}\!)$ is injective.
$H^0(k,R^i q_*G_X\!)\to H^{i}(X_{\bar {k}},G_{X_{\bar {k}}}\!)$ is injective.
Proof. Let ![]() ${\mathcal {H}}^i(q,G_{X}\!)$ be the higher presheaf pushforward of
${\mathcal {H}}^i(q,G_{X}\!)$ be the higher presheaf pushforward of ![]() $G_{X}$ on
$G_{X}$ on ![]() $X$ with respect to
$X$ with respect to ![]() $q$. We first want to prove that
$q$. We first want to prove that ![]() ${\mathcal {H}}^i(q,G_{X}\!)$ is finitary for
${\mathcal {H}}^i(q,G_{X}\!)$ is finitary for ![]() $i\geq 0$. In other words, we want to prove that for every inverse system
$i\geq 0$. In other words, we want to prove that for every inverse system ![]() $\{T^{(\ell )}\}_{\ell \in L}$ of quasi-compact quasi-separated
$\{T^{(\ell )}\}_{\ell \in L}$ of quasi-compact quasi-separated ![]() $k$-schemes, the natural morphism
$k$-schemes, the natural morphism
is an isomorphism, where ![]() $X^{(\ell )}:=X\times _k T^{(\ell )}$ and
$X^{(\ell )}:=X\times _k T^{(\ell )}$ and ![]() $X^{(\infty )}:=\lim _{\ell \in L}X^{(\ell )}$. By [Sta23, Tag 01H0],
$X^{(\infty )}:=\lim _{\ell \in L}X^{(\ell )}$. By [Sta23, Tag 01H0],
for every ![]() $\ell \in L \coprod \{\infty \}$, where
$\ell \in L \coprod \{\infty \}$, where ![]() $\mathrm {HC}(X^{(\ell )})$ is the category of fppf hypercoverings of
$\mathrm {HC}(X^{(\ell )})$ is the category of fppf hypercoverings of ![]() $X^{(\ell )}$. Since each
$X^{(\ell )}$. Since each ![]() $X^{(\ell )}$ is quasi-compact quasi-separated, by [Sta23, Tag 021P] we can replace the category
$X^{(\ell )}$ is quasi-compact quasi-separated, by [Sta23, Tag 021P] we can replace the category ![]() $\mathrm {HC}(X^{(\ell )})$ in the colimit with the subcategory
$\mathrm {HC}(X^{(\ell )})$ in the colimit with the subcategory ![]() $\mathrm {HC}(X^{(\ell )})^{\mathrm {qcqs}}$, consisting of those hypercoverings such that
$\mathrm {HC}(X^{(\ell )})^{\mathrm {qcqs}}$, consisting of those hypercoverings such that ![]() $U^{(\ell )}_n$ is quasi-compact quasi-separated for every
$U^{(\ell )}_n$ is quasi-compact quasi-separated for every ![]() $n\geq 0$. By [Sta23, Lemma 01ZM], for
$n\geq 0$. By [Sta23, Lemma 01ZM], for ![]() $U^{(\infty )}_\bullet \in \mathrm {HC}(X^{(\infty )})^{\mathrm {qcqs}}$ and
$U^{(\infty )}_\bullet \in \mathrm {HC}(X^{(\infty )})^{\mathrm {qcqs}}$ and ![]() $n\geq 0$ there exists an
$n\geq 0$ there exists an ![]() $\ell \in L$ and
$\ell \in L$ and ![]() $U_\bullet ^{(\ell,n)}\in \mathrm {HC}(X^{(\ell )})^{\mathrm {qcqs}}$ such that
$U_\bullet ^{(\ell,n)}\in \mathrm {HC}(X^{(\ell )})^{\mathrm {qcqs}}$ such that
where ![]() $\mathrm {tr}_n(-)$ denotes the
$\mathrm {tr}_n(-)$ denotes the ![]() $n$th truncation of simplicial schemes and
$n$th truncation of simplicial schemes and ![]() $T^{(\infty )}:=\lim _{\ell \in L}T^{(\ell )}$. This implies that
$T^{(\infty )}:=\lim _{\ell \in L}T^{(\ell )}$. This implies that
We are reduced to proving that for every ![]() $\ell \in L$ and
$\ell \in L$ and ![]() $U_\bullet ^{(\ell )}\in \mathrm {HC}(X^{(\ell )})^{\mathrm {qcqs}}$ we have that
$U_\bullet ^{(\ell )}\in \mathrm {HC}(X^{(\ell )})^{\mathrm {qcqs}}$ we have that
Since ![]() $G$ is of finite type over
$G$ is of finite type over ![]() $k$, this follows from [Sta23, Lemma 01ZM] and the exactness of filtered colimits.
$k$, this follows from [Sta23, Lemma 01ZM] and the exactness of filtered colimits.
Knowing that ![]() ${\mathcal {H}}^i(q,G_{X}\!)$ is finitary, in order to prove that
${\mathcal {H}}^i(q,G_{X}\!)$ is finitary, in order to prove that ![]() $R^iq_*G_X\!$ is finitary as well it is enough to prove that for every finitary presheaf
$R^iq_*G_X\!$ is finitary as well it is enough to prove that for every finitary presheaf ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $(\mathbf {Sch}^{\mathrm {qcqs}}/k)_{\mathrm {fppf}}$, the ‘partial’ sheafification
$(\mathbf {Sch}^{\mathrm {qcqs}}/k)_{\mathrm {fppf}}$, the ‘partial’ sheafification ![]() $\mathcal {F}^+$ (defined as in [Sta23, § 00W1]) is finitary. Similarly to the previous paragraph, the proof of this fact follows from the observation that each finite quasi-compact quasi-separated fppf covering of
$\mathcal {F}^+$ (defined as in [Sta23, § 00W1]) is finitary. Similarly to the previous paragraph, the proof of this fact follows from the observation that each finite quasi-compact quasi-separated fppf covering of ![]() $X^{(\infty )}$ descends to a covering of
$X^{(\infty )}$ descends to a covering of ![]() $X^{(\ell )}$ for some
$X^{(\ell )}$ for some ![]() $\ell \in L$ and Čech cohomology commutes with filtered colimits (
$\ell \in L$ and Čech cohomology commutes with filtered colimits (![]() $\check {H}^0$ is enough in this case).
$\check {H}^0$ is enough in this case).
For the second part, we note that for every presheaf ![]() $\mathcal {F}$ on
$\mathcal {F}$ on ![]() $(\mathbf {Sch}/k)_{\mathrm {fppf}}$ with sheafification
$(\mathbf {Sch}/k)_{\mathrm {fppf}}$ with sheafification ![]() $\mathcal {F}^\sharp$, the natural morphism
$\mathcal {F}^\sharp$, the natural morphism
is an isomorphism because every fppf covering of ![]() $\operatorname {Spec}({\bar {k}})$ admits a section. This implies that
$\operatorname {Spec}({\bar {k}})$ admits a section. This implies that
Thanks to the previous part, we deduce that the composition
is injective, where the colimit runs over all finite field extensions of ![]() $k$. This ends the proof.
$k$. This ends the proof.
With the previous results we can prove [Reference GrothendieckGro68, Proposition 5.6], which was stated by Grothendieck without a complete proof.Footnote 4
Corollary 3.4 If ![]() $k$ is separably closed and
$k$ is separably closed and ![]() $X$ is a proper
$X$ is a proper ![]() $k$-scheme, then there is a natural exact sequence
$k$-scheme, then there is a natural exact sequence
In particular, if ![]() $\mathrm {Pic}_{X/k}$ is smooth, then the natural morphism
$\mathrm {Pic}_{X/k}$ is smooth, then the natural morphism ![]() $\mathrm {Br}(X)\to \mathrm {Br}(X_{{\bar {k}}})$ is injective.
$\mathrm {Br}(X)\to \mathrm {Br}(X_{{\bar {k}}})$ is injective.
Proof. As in Lemma 3.1, we consider the Leray spectral sequence
Since ![]() $X$ is proper over
$X$ is proper over ![]() $k$, by [Sta23, Tag 0BUG] we deduce that
$k$, by [Sta23, Tag 0BUG] we deduce that ![]() $A:=H^0(X,\mathcal {O}_X\!)$ is a finite
$A:=H^0(X,\mathcal {O}_X\!)$ is a finite ![]() $k$-algebra. This implies that
$k$-algebra. This implies that ![]() $q_*\mathbb {G}_m$ is represented by a smooth group scheme over
$q_*\mathbb {G}_m$ is represented by a smooth group scheme over ![]() $k$. Thanks to [Reference GrothendieckGro68, Theorem 11.7], we deduce that
$k$. Thanks to [Reference GrothendieckGro68, Theorem 11.7], we deduce that ![]() $E^{i,j}_2=0$ for
$E^{i,j}_2=0$ for ![]() $i>0$ and
$i>0$ and ![]() $j=0$, so that
$j=0$, so that ![]() $E^{1,1}_2=E^{1,1}_\infty$. The Leray spectral sequence produces then the exact sequence
$E^{1,1}_2=E^{1,1}_\infty$. The Leray spectral sequence produces then the exact sequence
To get the first part of the statement it is then enough to apply Lemma 3.3. For the second part, we note that when ![]() $\mathrm {Pic}_{X/{k}}$ is smooth, thanks to [Reference GrothendieckGro68, Theorem 11.7], the group
$\mathrm {Pic}_{X/{k}}$ is smooth, thanks to [Reference GrothendieckGro68, Theorem 11.7], the group ![]() $H^1(k,\mathrm {Pic}_{X/{k}})$ vanishes.
$H^1(k,\mathrm {Pic}_{X/{k}})$ vanishes.
Definition 3.5 For a scheme ![]() $X$ over
$X$ over ![]() $k$ and a prime
$k$ and a prime ![]() $p$, we define
$p$, we define ![]() $H^2(X,\mathbb {Z}_p(1))$ as the projective limit
$H^2(X,\mathbb {Z}_p(1))$ as the projective limit
Remark 3.6 Note that we are defining ![]() $H^2(X,\mathbb {Z}_p(1))$ without taking into account higher inverse limits. Nonetheless, if
$H^2(X,\mathbb {Z}_p(1))$ without taking into account higher inverse limits. Nonetheless, if ![]() $k$ is algebraically closed of characteristic
$k$ is algebraically closed of characteristic ![]() $p$ and
$p$ and ![]() $X$ is smooth and proper over
$X$ is smooth and proper over ![]() $k$, then
$k$, then ![]() $R^1\varprojlim _n H^1(X,{\mu _{p^n}}\!)=R^1\varprojlim _n \mathrm {Pic}(X)[p^n]=0$ since
$R^1\varprojlim _n H^1(X,{\mu _{p^n}}\!)=R^1\varprojlim _n \mathrm {Pic}(X)[p^n]=0$ since ![]() $\mathrm {Pic}(X)[p^\infty ]$ is a direct sum of a
$\mathrm {Pic}(X)[p^\infty ]$ is a direct sum of a ![]() $p$-divisible group and a finite group and
$p$-divisible group and a finite group and ![]() $R^1\varprojlim _n H^2(X,{\mu _{p^n}}\!)=0$ by [Reference IllusieIll79, Chapter II, Proposition 5.9].
$R^1\varprojlim _n H^2(X,{\mu _{p^n}}\!)=0$ by [Reference IllusieIll79, Chapter II, Proposition 5.9].
Construction 3.7 The Kummer exact sequences for ![]() $X$ and
$X$ and ![]() $X_{{\bar {k}}}$ (for the fppf topology) induce the following commutative diagram with exact rows.
$X_{{\bar {k}}}$ (for the fppf topology) induce the following commutative diagram with exact rows.

We write
for the complex obtained by taking images of the vertical arrows. Note that a priori ![]() $(\mathrm {Br}(X_{{\bar {k}}})[p^n])^{k}$ is smaller than
$(\mathrm {Br}(X_{{\bar {k}}})[p^n])^{k}$ is smaller than ![]() $\mathrm {Br}(X_{\bar {k}})^k[p^n]$, where
$\mathrm {Br}(X_{\bar {k}})^k[p^n]$, where ![]() $\mathrm {Br}(X_{\bar {k}})^k:=\mathrm {im}(\mathrm {Br}(X)\to \mathrm {Br}(X_{\bar {k}}))$.
$\mathrm {Br}(X_{\bar {k}})^k:=\mathrm {im}(\mathrm {Br}(X)\to \mathrm {Br}(X_{\bar {k}}))$.
Since both ![]() $R^1\varprojlim _{n}\mathrm {Pic}(X)/p^n$ and
$R^1\varprojlim _{n}\mathrm {Pic}(X)/p^n$ and ![]() $R^1\varprojlim _{n}\mathrm {Pic}(X_{\bar {k}})/p^n$ vanish, we can also consider the following commutative diagram with exact rows:
$R^1\varprojlim _{n}\mathrm {Pic}(X_{\bar {k}})/p^n$ vanish, we can also consider the following commutative diagram with exact rows:

obtained by taking the projective limit of the diagrams (3.7.1) for various ![]() $n$. We denote by
$n$. We denote by
the complex obtained by taking images of the vertical arrows.
Proposition 3.8 If ![]() $\mathrm {char}(k)=p$ and
$\mathrm {char}(k)=p$ and ![]() $A$ is an abelian variety over
$A$ is an abelian variety over ![]() $k$ such that the morphism
$k$ such that the morphism ![]() $\mathrm {Pic}(A)\to \mathrm {NS}(A_{{\bar {k}}})$ is surjective, then the complexes
$\mathrm {Pic}(A)\to \mathrm {NS}(A_{{\bar {k}}})$ is surjective, then the complexes ![]() $C_n(A)$ and
$C_n(A)$ and ![]() $\hat {C}(A)$ are acyclic.
$\hat {C}(A)$ are acyclic.
Proof. If ![]() $K_{1,n}$ is the kernel of
$K_{1,n}$ is the kernel of ![]() $H^2_{}(A,{\mu _{p^n}}\!)\to H^2(A_{\bar {k}},{\mu _{p^n}}\!)$ and
$H^2_{}(A,{\mu _{p^n}}\!)\to H^2(A_{\bar {k}},{\mu _{p^n}}\!)$ and ![]() $K_{2}$ is the kernel of
$K_{2}$ is the kernel of ![]() $\mathrm {Br}(A)\to \mathrm {Br}(A_{\bar {k}})$, in order to prove that
$\mathrm {Br}(A)\to \mathrm {Br}(A_{\bar {k}})$, in order to prove that ![]() $C_n(A)$ is acyclic we have to show that
$C_n(A)$ is acyclic we have to show that ![]() $K_{1,n}\to K_{2}[p^n]$ is surjective. Combining Lemmas 3.1 and 3.3, we deduce the following commutative diagram with exact rows.
$K_{1,n}\to K_{2}[p^n]$ is surjective. Combining Lemmas 3.1 and 3.3, we deduce the following commutative diagram with exact rows.

The morphism of exact sequences factors through the complex
which is acyclic because ![]() $\mathrm {Br}(k)$ is
$\mathrm {Br}(k)$ is ![]() $p$-divisible by [Reference Colliot-Thélène and SkorobogatovCS21, Theorem 1.3.7]. The image of
$p$-divisible by [Reference Colliot-Thélène and SkorobogatovCS21, Theorem 1.3.7]. The image of
is ![]() $H^1_{}(k,\mathrm {Pic}_{A/k}^\circ )[p^n]$, thus we are reduced to prove that
$H^1_{}(k,\mathrm {Pic}_{A/k}^\circ )[p^n]$, thus we are reduced to prove that
is surjective. Since ![]() $\mathrm {Pic}(A)\to \mathrm {NS}(A_{\bar {k}})$ is surjective, we know that
$\mathrm {Pic}(A)\to \mathrm {NS}(A_{\bar {k}})$ is surjective, we know that ![]() $\pi _0(\mathrm {Pic}_{A/k})$ is a constant finitely generated torsion-free group over
$\pi _0(\mathrm {Pic}_{A/k})$ is a constant finitely generated torsion-free group over ![]() $k$ such that
$k$ such that ![]() $\mathrm {Pic}_{A/k}(k)\to \pi _0(\mathrm {Pic}_{A/k})(k)$ is surjective. Looking at the cohomology long exact sequence associated to
$\mathrm {Pic}_{A/k}(k)\to \pi _0(\mathrm {Pic}_{A/k})(k)$ is surjective. Looking at the cohomology long exact sequence associated to
we then deduce that ![]() $H^1_{}(k,\mathrm {Pic}_{A/k}^\circ )\xrightarrow {\sim } H^1_{}(k,\mathrm {Pic}_{A/k})$, which yields the desired result.
$H^1_{}(k,\mathrm {Pic}_{A/k}^\circ )\xrightarrow {\sim } H^1_{}(k,\mathrm {Pic}_{A/k})$, which yields the desired result.
We now prove that ![]() $\hat {C}(A)$ is acyclic. The kernel of
$\hat {C}(A)$ is acyclic. The kernel of ![]() $H^2(A,{\mathbb {Z}_{p}}(1))\to H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))$ is
$H^2(A,{\mathbb {Z}_{p}}(1))\to H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))$ is ![]() $\varprojlim _n K_{1,n}$ and the kernel of
$\varprojlim _n K_{1,n}$ and the kernel of ![]() $\mathrm {T}_p(\mathrm {Br}(A))\to \mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ is
$\mathrm {T}_p(\mathrm {Br}(A))\to \mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ is ![]() $\mathrm {T}_p(K_2)$. Thus, again, we have to prove that
$\mathrm {T}_p(K_2)$. Thus, again, we have to prove that ![]() $\varprojlim _n K_{1,n}\to \mathrm {T}_p(K_2)$ is surjective. Combining the previous discussion and the fact that
$\varprojlim _n K_{1,n}\to \mathrm {T}_p(K_2)$ is surjective. Combining the previous discussion and the fact that ![]() $\mathrm {Br}(k)$ is
$\mathrm {Br}(k)$ is ![]() $p$-divisible, we deduce that the two groups sit in the following diagram with exact rows.
$p$-divisible, we deduce that the two groups sit in the following diagram with exact rows.

For every ![]() $n>0$, the kernel of
$n>0$, the kernel of ![]() $H^1_{}(k,\mathrm {Pic}_{A/k}[p^n]) \to H^1_{}(k,\mathrm {Pic}_{A/k})[p^n]$ is
$H^1_{}(k,\mathrm {Pic}_{A/k}[p^n]) \to H^1_{}(k,\mathrm {Pic}_{A/k})[p^n]$ is ![]() $\mathrm {Pic}(A)/p^n$ and the groups
$\mathrm {Pic}(A)/p^n$ and the groups ![]() $(\mathrm {Pic}(A)/p^n)_{n>0}$ form a Mittag–Leffler system. We deduce that the morphism
$(\mathrm {Pic}(A)/p^n)_{n>0}$ form a Mittag–Leffler system. We deduce that the morphism
is surjective. This implies that ![]() $\hat {C}(A)$ is acyclic, as we wanted.
$\hat {C}(A)$ is acyclic, as we wanted.
The proof of the following proposition was inspired by [Reference Colliot-Thélène and SkorobogatovCS13, Theorem 2.1].
Proposition 3.9 If ![]() $\mathrm {char}(k)=p$ and
$\mathrm {char}(k)=p$ and ![]() $A$ is an abelian variety over
$A$ is an abelian variety over ![]() $k$, we have
$k$, we have ![]() $H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))^{k}[\frac {1}{p}]=(\varprojlim _{n}H^2(A_{\bar {k}},{\mu _{p^n}}\!)^{k})[\frac {1}{p}]$ and
$H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))^{k}[\frac {1}{p}]=(\varprojlim _{n}H^2(A_{\bar {k}},{\mu _{p^n}}\!)^{k})[\frac {1}{p}]$ and ![]() $\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}}))^{k}[\frac {1}{p}]=\mathrm {V}_p(\mathrm {Br}(A_{{\bar {k}}})^{k}).$
$\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}}))^{k}[\frac {1}{p}]=\mathrm {V}_p(\mathrm {Br}(A_{{\bar {k}}})^{k}).$
Proof. We first note that the four ![]() ${\mathbb {Q}_{p}}$-vector spaces are invariant under isogenies of
${\mathbb {Q}_{p}}$-vector spaces are invariant under isogenies of ![]() $A$ and finite separable extension of
$A$ and finite separable extension of ![]() $k$. Indeed, for every isogeny
$k$. Indeed, for every isogeny ![]() $\varphi :B\to A$ there exists an isogeny
$\varphi :B\to A$ there exists an isogeny ![]() $\psi : A\to B$ such that the composition
$\psi : A\to B$ such that the composition ![]() $\varphi \circ \psi$ is the multiplication by some positive integer
$\varphi \circ \psi$ is the multiplication by some positive integer ![]() $n$. Since
$n$. Since ![]() $n$ is invertible in
$n$ is invertible in ![]() ${\mathbb {Q}_{p}}$, we deduce that
${\mathbb {Q}_{p}}$, we deduce that ![]() $\varphi ^*$ is an isomorphism at the level of cohomology groups. Similarly, if
$\varphi ^*$ is an isomorphism at the level of cohomology groups. Similarly, if ![]() $k'/k$ is a finite separable extension, then the pullback morphisms with respect to
$k'/k$ is a finite separable extension, then the pullback morphisms with respect to ![]() $A_{k'}\to A$ admit as inverse the morphisms
$A_{k'}\to A$ admit as inverse the morphisms ![]() $ ({1}/{[k':k]})\mathrm {Tr}_{A_{k'}/A}$.
$ ({1}/{[k':k]})\mathrm {Tr}_{A_{k'}/A}$.
Next, thanks to [Reference KatzKat99, Theorem 11], we note that there exists a proper smooth connected curve ![]() $C$ with a rational point and a morphism
$C$ with a rational point and a morphism ![]() $C\to A$ such that
$C\to A$ such that ![]() $B:=\mathrm {Jac}(C)$ maps surjectively to
$B:=\mathrm {Jac}(C)$ maps surjectively to ![]() $A$. By Poincaré's complete reducibility theorem,
$A$. By Poincaré's complete reducibility theorem, ![]() $B$ is isogenous to a product
$B$ is isogenous to a product ![]() $A\times _k A'$ with
$A\times _k A'$ with ![]() $A'$ an abelian variety over
$A'$ an abelian variety over ![]() $k$. Since
$k$. Since ![]() $H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))^{k}$ (respectively,
$H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))^{k}$ (respectively, ![]() $\mathrm {Br}(A_{{\bar {k}}})^k$) is a direct summand of
$\mathrm {Br}(A_{{\bar {k}}})^k$) is a direct summand of ![]() $H^2(A_{\bar {k}}\times _{\bar {k}} A'_{\bar {k}},{\mathbb {Z}_{p}}(1))^{k}$ (respectively,
$H^2(A_{\bar {k}}\times _{\bar {k}} A'_{\bar {k}},{\mathbb {Z}_{p}}(1))^{k}$ (respectively, ![]() $\mathrm {Br}(A_{\bar {k}}\times _{\bar {k}} A'_{{\bar {k}}})^k$) and the property we want to prove is invariant by isogenies, it is then enough to prove the result for
$\mathrm {Br}(A_{\bar {k}}\times _{\bar {k}} A'_{{\bar {k}}})^k$) and the property we want to prove is invariant by isogenies, it is then enough to prove the result for ![]() $B$. In addition, since in the statement it is harmless to extend
$B$. In addition, since in the statement it is harmless to extend ![]() $k$ to a finite separable extension, we may assume that
$k$ to a finite separable extension, we may assume that ![]() $\mathrm {Pic}(B)\to \mathrm {NS}(B_{{\bar {k}}})$ is surjective, so that
$\mathrm {Pic}(B)\to \mathrm {NS}(B_{{\bar {k}}})$ is surjective, so that ![]() $H^1(k,\mathrm {Pic}^0_{B/k})=H^1(k,\mathrm {Pic}_{B/k})$.
$H^1(k,\mathrm {Pic}^0_{B/k})=H^1(k,\mathrm {Pic}_{B/k})$.
Let ![]() $K_{1,n}$ be the kernel of the morphism
$K_{1,n}$ be the kernel of the morphism ![]() $H^2(B,{\mu _{p^n}}\!)\to H^2(B_{\bar {k}},{\mu _{p^n}}\!)$. By Lemmas 3.1 and 3.3, the group
$H^2(B,{\mu _{p^n}}\!)\to H^2(B_{\bar {k}},{\mu _{p^n}}\!)$. By Lemmas 3.1 and 3.3, the group ![]() $K_{1,n}$ is an extension of
$K_{1,n}$ is an extension of ![]() $H^1(k,\mathrm {Pic}_{B/k}[p^n])$ by
$H^1(k,\mathrm {Pic}_{B/k}[p^n])$ by ![]() $\mathrm {Br}(k)[p^n]$ and by the assumption
$\mathrm {Br}(k)[p^n]$ and by the assumption ![]() $\mathrm {Pic}_{C/k}[p^n]=\mathrm {Pic}_{B/k}[p^n]$. We deduce that
$\mathrm {Pic}_{C/k}[p^n]=\mathrm {Pic}_{B/k}[p^n]$. We deduce that ![]() $K_{1,n}=\ker (H^2(C,{\mu _{p^n}}\!)\to H^2(C_{\bar {k}},{\mu _{p^n}}\!))$. By [Reference GrothendieckGro68, Rmq. 2.5.b], the group
$K_{1,n}=\ker (H^2(C,{\mu _{p^n}}\!)\to H^2(C_{\bar {k}},{\mu _{p^n}}\!))$. By [Reference GrothendieckGro68, Rmq. 2.5.b], the group ![]() $\mathrm {Br}(C_{\bar {k}})$ vanishes, thus
$\mathrm {Br}(C_{\bar {k}})$ vanishes, thus ![]() $H^2(C_{{\bar {k}}},{\mathbb {Z}_{p}}(1))={\mathbb {Z}_{p}}$ and the morphism
$H^2(C_{{\bar {k}}},{\mathbb {Z}_{p}}(1))={\mathbb {Z}_{p}}$ and the morphism ![]() $H^2(C,{\mathbb {Z}_{p}}(1))\to H^2(C_{{\bar {k}}},{\mathbb {Z}_{p}}(1))$ is surjective because
$H^2(C,{\mathbb {Z}_{p}}(1))\to H^2(C_{{\bar {k}}},{\mathbb {Z}_{p}}(1))$ is surjective because ![]() $C$ has a rational point. This implies that
$C$ has a rational point. This implies that ![]() $R^1 \varprojlim _{n}K_{1,n}\to R^1 \varprojlim _{n}H^2(C,{\mu _{p^n}}\!)$ is injective. Since
$R^1 \varprojlim _{n}K_{1,n}\to R^1 \varprojlim _{n}H^2(C,{\mu _{p^n}}\!)$ is injective. Since
factors through ![]() $R^1 \varprojlim _{n}H^2(B,{\mu _{p^n}}\!),$ we deduce that
$R^1 \varprojlim _{n}H^2(B,{\mu _{p^n}}\!),$ we deduce that ![]() $R^1 \varprojlim _{n}K_{1,n}\to R^1 \varprojlim _{n}H^2(B,{\mu _{p^n}}\!)$ is injective as well. Therefore, the morphism
$R^1 \varprojlim _{n}K_{1,n}\to R^1 \varprojlim _{n}H^2(B,{\mu _{p^n}}\!)$ is injective as well. Therefore, the morphism ![]() $H^2(B,{\mathbb {Z}_{p}}(1))\to \varprojlim _{n}H^2(B_{\bar {k}},{\mu _{p^n}}\!)^{k}$ is surjective. Thanks to Proposition 3.8, for every
$H^2(B,{\mathbb {Z}_{p}}(1))\to \varprojlim _{n}H^2(B_{\bar {k}},{\mu _{p^n}}\!)^{k}$ is surjective. Thanks to Proposition 3.8, for every ![]() $n$ the morphism
$n$ the morphism ![]() $H^2(B_{\bar {k}},{\mu _{p^n}}\!)^{k}\to (\mathrm {Br}(B_{\bar {k}})[p^n])^k$ is surjective with finite kernel, so that
$H^2(B_{\bar {k}},{\mu _{p^n}}\!)^{k}\to (\mathrm {Br}(B_{\bar {k}})[p^n])^k$ is surjective with finite kernel, so that ![]() $\varprojlim _{n}H^2(B_{\bar {k}},{\mu _{p^n}}\!)^{k}\to \varprojlim _n(\mathrm {Br}(B_{\bar {k}})[p^n])^k$ is surjective as well. This implies that
$\varprojlim _{n}H^2(B_{\bar {k}},{\mu _{p^n}}\!)^{k}\to \varprojlim _n(\mathrm {Br}(B_{\bar {k}})[p^n])^k$ is surjective as well. This implies that ![]() $\mathrm {T}_p(\mathrm {Br}(B_{{\bar {k}}}))^{k}\to \varprojlim _n(\mathrm {Br}(B_{\bar {k}})[p^n])^k$ is surjective.
$\mathrm {T}_p(\mathrm {Br}(B_{{\bar {k}}}))^{k}\to \varprojlim _n(\mathrm {Br}(B_{\bar {k}})[p^n])^k$ is surjective.
It remains to prove that for every ![]() $n$ we have
$n$ we have ![]() $(\mathrm {Br}(B_{\bar {k}})[p^n])^k=\mathrm {Br}(B_{\bar {k}})^k[p^n]$. Consider the natural morphism
$(\mathrm {Br}(B_{\bar {k}})[p^n])^k=\mathrm {Br}(B_{\bar {k}})^k[p^n]$. Consider the natural morphism ![]() $K_3\to \mathrm {Br}(C)$ where
$K_3\to \mathrm {Br}(C)$ where ![]() $K_3$ is the kernel of
$K_3$ is the kernel of ![]() $\mathrm {Br}(B)\to \mathrm {Br}(B_{{\bar {k}}})$. Thanks to Lemmas 3.1 and 3.3 and using the fact that
$\mathrm {Br}(B)\to \mathrm {Br}(B_{{\bar {k}}})$. Thanks to Lemmas 3.1 and 3.3 and using the fact that ![]() $\mathrm {Br}(C_{\bar {k}})=0$, this morphism sits in the following commutative diagram with exact rows.
$\mathrm {Br}(C_{\bar {k}})=0$, this morphism sits in the following commutative diagram with exact rows.

Since ![]() $\mathrm {Pic}(B)\to \mathrm {NS}(B_{\bar {k}})$ is surjective and
$\mathrm {Pic}(B)\to \mathrm {NS}(B_{\bar {k}})$ is surjective and ![]() $C$ is a curve, we have that
$C$ is a curve, we have that
We deduce that ![]() $K_3\to \mathrm {Br}(C)$ is an isomorphism, thus
$K_3\to \mathrm {Br}(C)$ is an isomorphism, thus ![]() $\mathrm {Br}(B)\to \mathrm {Br}(C)\xrightarrow {\sim } K_3$ provides a splitting of the exact sequence
$\mathrm {Br}(B)\to \mathrm {Br}(C)\xrightarrow {\sim } K_3$ provides a splitting of the exact sequence
This implies that ![]() $\mathrm {Br}(B)[p^n]\to \mathrm {Br}(B_{{\bar {k}}})^k[p^n]$ is surjective and this yields the desired result.
$\mathrm {Br}(B)[p^n]\to \mathrm {Br}(B_{{\bar {k}}})^k[p^n]$ is surjective and this yields the desired result.
4. Constructing a morphism
Let ![]() $A$ be an abelian variety over a field
$A$ be an abelian variety over a field ![]() $k$. For a line bundle
$k$. For a line bundle ![]() $\mathcal {L}$ of
$\mathcal {L}$ of ![]() $A$ we write
$A$ we write ![]() $\varphi _{\mathcal {L}}:A\to A^\vee$ for the morphism which sends
$\varphi _{\mathcal {L}}:A\to A^\vee$ for the morphism which sends ![]() $x\mapsto t_x^*\mathcal {L}\otimes \mathcal {L}^{-1}$, where
$x\mapsto t_x^*\mathcal {L}\otimes \mathcal {L}^{-1}$, where ![]() $t_x$ is the translation by
$t_x$ is the translation by ![]() $x$. In this section we want to complete the following solid square.
$x$. In this section we want to complete the following solid square.

If ![]() $k$ is an algebraically closed field of characteristic
$k$ is an algebraically closed field of characteristic ![]() $0$ such a commutative diagram is constructed in [Reference Orr, Skorobogatov and ZarhinOSZ21, Lemma 2.6] using an analytic method. We propose instead an algebraic construction which works for any field.
$0$ such a commutative diagram is constructed in [Reference Orr, Skorobogatov and ZarhinOSZ21, Lemma 2.6] using an analytic method. We propose instead an algebraic construction which works for any field.
4.1
Consider the morphism ![]() $h_1:H^2(A,{\mu _{p^n}}\!)\to H^2(A\times _k A,{\mu _{p^n}}\!)$ which sends a class
$h_1:H^2(A,{\mu _{p^n}}\!)\to H^2(A\times _k A,{\mu _{p^n}}\!)$ which sends a class ![]() $\alpha$ to
$\alpha$ to ![]() $m^*(\alpha )-\pi _1^*(\alpha )-\pi _2^*(\alpha )$, where
$m^*(\alpha )-\pi _1^*(\alpha )-\pi _2^*(\alpha )$, where ![]() $\pi _1$ and
$\pi _1$ and ![]() $\pi _2$ are the two projections of
$\pi _2$ are the two projections of ![]() $A\times _k A$. This morphism has the property that the first Chern class
$A\times _k A$. This morphism has the property that the first Chern class ![]() $c_1(\mathcal {L})\in H^2(A,{\mu _{p^n}}\!)$ of a line bundle
$c_1(\mathcal {L})\in H^2(A,{\mu _{p^n}}\!)$ of a line bundle ![]() $\mathcal {L}$ is sent to
$\mathcal {L}$ is sent to ![]() $c_1(\Lambda (\mathcal {L}))$, the first Chern class of the associated Mumford bundle
$c_1(\Lambda (\mathcal {L}))$, the first Chern class of the associated Mumford bundle ![]() $\Lambda (\mathcal {L}):=m^*\mathcal {L}\otimes \pi _1^*\mathcal {L}^{-1}\otimes \pi _2^*\mathcal {L}^{-1}$. The Leray spectral sequence
$\Lambda (\mathcal {L}):=m^*\mathcal {L}\otimes \pi _1^*\mathcal {L}^{-1}\otimes \pi _2^*\mathcal {L}^{-1}$. The Leray spectral sequence
induces a filtration ![]() $0\subseteq F^2 H^{2}(A\times _k A,{\mu _{p^n}}\!) \subseteq F^1 H^{2}(A\times _k A,{\mu _{p^n}}\!)\subseteq H^{2}(A\times _k A,{\mu _{p^n}}\!)$.
$0\subseteq F^2 H^{2}(A\times _k A,{\mu _{p^n}}\!) \subseteq F^1 H^{2}(A\times _k A,{\mu _{p^n}}\!)\subseteq H^{2}(A\times _k A,{\mu _{p^n}}\!)$.
Lemma 4.2 The image of ![]() $h_1$ lies in
$h_1$ lies in ![]() $F^1H^{2}(A\times _k A,{\mu _{p^n}}\!)$.
$F^1H^{2}(A\times _k A,{\mu _{p^n}}\!)$.
Proof. The spectral sequence (4.1.1) gives the exact sequence
Therefore, it is enough to check that the composition
is the ![]() $0$-morphism. By [Reference Bragg and OlssonBO21, Corollary 1.4], there exists a commutative linear algebraic groupFootnote 5
$0$-morphism. By [Reference Bragg and OlssonBO21, Corollary 1.4], there exists a commutative linear algebraic groupFootnote 5 ![]() $G$ over
$G$ over ![]() $k$ which represents
$k$ which represents ![]() $R^2q_{*}{\mu _{p^n}}$ on the big fppf site
$R^2q_{*}{\mu _{p^n}}$ on the big fppf site ![]() $(\mathbf {Sch}/k)_{\mathrm {fppf}}$. Since
$(\mathbf {Sch}/k)_{\mathrm {fppf}}$. Since ![]() $R^2\pi _{2*}{\mu _{p^n}}$ is the restriction of
$R^2\pi _{2*}{\mu _{p^n}}$ is the restriction of ![]() $R^2q_{*}{\mu _{p^n}}$ from
$R^2q_{*}{\mu _{p^n}}$ from ![]() $(\mathbf {Sch}/k)_{\mathrm {fppf}}$ to
$(\mathbf {Sch}/k)_{\mathrm {fppf}}$ to ![]() $(\mathbf {Sch}/A)_{\mathrm {fppf}}$, this implies that
$(\mathbf {Sch}/A)_{\mathrm {fppf}}$, this implies that ![]() $H^0(A,R^2\pi _{2*}{\mu _{p^n}}\!)$ can be computed as
$H^0(A,R^2\pi _{2*}{\mu _{p^n}}\!)$ can be computed as ![]() $\mathrm {Mor}_{\mathbf {Sch}/k}(A,G)$. Thanks to the fact that
$\mathrm {Mor}_{\mathbf {Sch}/k}(A,G)$. Thanks to the fact that ![]() $G$ is affine, every morphism
$G$ is affine, every morphism ![]() $A\to G$ contracts
$A\to G$ contracts ![]() $A$ to a point. We deduce that
$A$ to a point. We deduce that ![]() $\mathrm {Mor}_{\mathbf {Sch}/k}(A,G)=\mathrm {Mor}_{\mathbf {Sch}/k}(0_A,G)=H^0(k,R^2q_{*}{\mu _{p^n}}\!)$. By Lemma 3.3, the group
$\mathrm {Mor}_{\mathbf {Sch}/k}(A,G)=\mathrm {Mor}_{\mathbf {Sch}/k}(0_A,G)=H^0(k,R^2q_{*}{\mu _{p^n}}\!)$. By Lemma 3.3, the group ![]() $H^0(k,R^2q_{*}{\mu _{p^n}}\!)$ is naturally a subgroup of
$H^0(k,R^2q_{*}{\mu _{p^n}}\!)$ is naturally a subgroup of ![]() $H^2(A_{\bar {k}},{\mu _{p^n}}\!)$ and the induced morphism
$H^2(A_{\bar {k}},{\mu _{p^n}}\!)$ and the induced morphism
is given by the pullback via ![]() $i_1:A=A\times _k 0_A \hookrightarrow A\times _k A$ followed by the extension of scalars to
$i_1:A=A\times _k 0_A \hookrightarrow A\times _k A$ followed by the extension of scalars to ![]() ${\bar {k}}$. By construction, we have that
${\bar {k}}$. By construction, we have that ![]() $i_1^*\circ h_1=i_1^*\circ m^*-i_1^*\circ \pi _1^*=0$. This concludes the proof.
$i_1^*\circ h_1=i_1^*\circ m^*-i_1^*\circ \pi _1^*=0$. This concludes the proof.
Lemma 4.3 Let ![]() $G$ be a finite commutative group scheme killed by a positive integer
$G$ be a finite commutative group scheme killed by a positive integer ![]() $n$. There is a natural injective morphism
$n$. There is a natural injective morphism ![]() $f_n:\operatorname {Hom}(A[n],G)\to H^1(A,G)$ which admits a retraction
$f_n:\operatorname {Hom}(A[n],G)\to H^1(A,G)$ which admits a retraction ![]() $g_n$.
$g_n$.
Proof. Write ![]() $P_{n}$ for the
$P_{n}$ for the ![]() $A[n]$-torsor over
$A[n]$-torsor over ![]() $A$ given by the multiplication by
$A$ given by the multiplication by ![]() $n$. The morphism
$n$. The morphism ![]() $f_n$ is then defined by
$f_n$ is then defined by ![]() $f_n(\sigma ):=\sigma _*P_{n}$ for every
$f_n(\sigma ):=\sigma _*P_{n}$ for every ![]() $\sigma \in \operatorname {Hom}(A[n],G)$. We want to define now
$\sigma \in \operatorname {Hom}(A[n],G)$. We want to define now ![]() $g_n$ which sends a
$g_n$ which sends a ![]() $G$-torsor
$G$-torsor ![]() $P$ over
$P$ over ![]() $A$ to an homomorphism
$A$ to an homomorphism ![]() $g_n(P): A[n]\to G$. By Cartier duality, this is the same as defining a morphism
$g_n(P): A[n]\to G$. By Cartier duality, this is the same as defining a morphism ![]() $g_n(P)^\vee :G^\vee \to (A[n])^\vee =A^\vee [n]$. For a scheme
$g_n(P)^\vee :G^\vee \to (A[n])^\vee =A^\vee [n]$. For a scheme ![]() $T$ over
$T$ over ![]() $k$ and a
$k$ and a ![]() $T$-point of
$T$-point of ![]() $G^\vee$ corresponding to a morphism
$G^\vee$ corresponding to a morphism ![]() $\tau :G_T\to \mathbb {G}_{m,T}$ we define
$\tau :G_T\to \mathbb {G}_{m,T}$ we define ![]() $g_n(P)^\vee (\tau )$ as
$g_n(P)^\vee (\tau )$ as ![]() $\tau _{*}P_T\in H^1(A_T,\mathbb {G}_{m,T})[n]=A^\vee [n](T)$. To prove that
$\tau _{*}P_T\in H^1(A_T,\mathbb {G}_{m,T})[n]=A^\vee [n](T)$. To prove that ![]() $g_n\circ f_n=\operatorname {id}$ it is enough to note that for every
$g_n\circ f_n=\operatorname {id}$ it is enough to note that for every ![]() $\sigma \in \operatorname {Hom}(A[n],G)$, every scheme
$\sigma \in \operatorname {Hom}(A[n],G)$, every scheme ![]() $T$ over
$T$ over ![]() $k$, and every
$k$, and every ![]() $\tau \in \operatorname {Hom}(G_T,\mathbb {G}_{m,T})$ we have that
$\tau \in \operatorname {Hom}(G_T,\mathbb {G}_{m,T})$ we have that ![]() $g_n(f_n(\sigma ))^\vee (\tau )=\tau _*(\sigma _*P_n)_T=(\tau \circ \sigma _T)_*P_{n,T}$ is the line bundle over
$g_n(f_n(\sigma ))^\vee (\tau )=\tau _*(\sigma _*P_n)_T=(\tau \circ \sigma _T)_*P_{n,T}$ is the line bundle over ![]() $A_T$ associated to
$A_T$ associated to ![]() $\tau \circ \sigma _T\in (A[n])^\vee (T)$ under the identification
$\tau \circ \sigma _T\in (A[n])^\vee (T)$ under the identification ![]() $(A[n])^\vee =A^\vee [n]$.
$(A[n])^\vee =A^\vee [n]$.
4.4
Thanks to Lemma 4.2, we can define
as the composition of ![]() $h_1$ and the natural morphism
$h_1$ and the natural morphism
In addition, by Lemma 4.3 applied to ![]() $G=A^\vee [p^n]$, we get a morphism
$G=A^\vee [p^n]$, we get a morphism
We write
for the composition ![]() ${h_2}\circ \bar {h}_1$ and we denote with the same letter the induced morphism
${h_2}\circ \bar {h}_1$ and we denote with the same letter the induced morphism ![]() $H^2(A,{\mathbb {Z}_{p}}(1))\to \operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$.
$H^2(A,{\mathbb {Z}_{p}}(1))\to \operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$.
Proposition 4.5 The square

is commutative.
Proof. We have to show that for every line bundle ![]() $\mathcal {L}\in \mathrm {Pic}(A)$ we have
$\mathcal {L}\in \mathrm {Pic}(A)$ we have
Consider the Leray spectral sequence
The morphism ![]() $A\times _k A\xrightarrow {\operatorname {id}_A\times \varphi _{\mathcal {L}}} A\times _k A^\vee$ induces via pullback a morphism from (4.5.2) to (4.1.1). This produces the commutative diagram
$A\times _k A\xrightarrow {\operatorname {id}_A\times \varphi _{\mathcal {L}}} A\times _k A^\vee$ induces via pullback a morphism from (4.5.2) to (4.1.1). This produces the commutative diagram

where the composition of the lower horizontal arrows is ![]() $h$. If
$h$. If ![]() $\mathcal {P}\in \mathrm {Pic}({A\times _k A^\vee })$ is the Poincaré bundle of
$\mathcal {P}\in \mathrm {Pic}({A\times _k A^\vee })$ is the Poincaré bundle of ![]() $A$, we have that
$A$, we have that ![]() $\Lambda (\mathcal {L})=(\operatorname {id}_A\times \varphi _{\mathcal {L}})^* \mathcal {P}$. This implies that
$\Lambda (\mathcal {L})=(\operatorname {id}_A\times \varphi _{\mathcal {L}})^* \mathcal {P}$. This implies that ![]() $h_1(c_1(\mathcal {L}))=c_1(\Lambda (\mathcal {L}))=(\operatorname {id}_A\times \varphi _{\mathcal {L}})^* c_1(\mathcal {P})$. In addition, by direct inspection, we note that
$h_1(c_1(\mathcal {L}))=c_1(\Lambda (\mathcal {L}))=(\operatorname {id}_A\times \varphi _{\mathcal {L}})^* c_1(\mathcal {P})$. In addition, by direct inspection, we note that ![]() $h_2(\varphi _{\mathcal {L}}^*([P]))=\varphi _\mathcal {L}|_{A[p^n]}$, where
$h_2(\varphi _{\mathcal {L}}^*([P]))=\varphi _\mathcal {L}|_{A[p^n]}$, where ![]() $[P]\in H^1(A^\vee,A^\vee [p^n])$ is the class of the torsor
$[P]\in H^1(A^\vee,A^\vee [p^n])$ is the class of the torsor ![]() $A^\vee \xrightarrow {\cdot p^n} A^\vee$. It remains to prove that the morphism
$A^\vee \xrightarrow {\cdot p^n} A^\vee$. It remains to prove that the morphism ![]() $F^1H^2(A\times _k A^\vee,{\mu _{p^n}}\!)\to H^1(A^\vee,A^\vee [p^n])$ sends
$F^1H^2(A\times _k A^\vee,{\mu _{p^n}}\!)\to H^1(A^\vee,A^\vee [p^n])$ sends ![]() $c_1(\mathcal {P})$ to
$c_1(\mathcal {P})$ to ![]() $[P]$. For this purpose, we introduce the Leray spectral sequence
$[P]$. For this purpose, we introduce the Leray spectral sequence
The morphism ![]() $\delta :\mathbb {G}_m[1]\to {\mu _{p^n}}$ associated to the Kummer exact sequence induces a morphism from (4.5.3) to (4.5.2) which we denote with the same symbol. In turn, this produces the following commutative diagram.
$\delta :\mathbb {G}_m[1]\to {\mu _{p^n}}$ associated to the Kummer exact sequence induces a morphism from (4.5.3) to (4.5.2) which we denote with the same symbol. In turn, this produces the following commutative diagram.

The upper horizontal arrow sends the line bundle ![]() $\mathcal {P}$ to
$\mathcal {P}$ to ![]() $\operatorname {id}_{A^\vee }\in H^0(A^\vee,A^\vee )$, while
$\operatorname {id}_{A^\vee }\in H^0(A^\vee,A^\vee )$, while ![]() $\delta$ sends
$\delta$ sends ![]() $\operatorname {id}_{A^\vee }$ to
$\operatorname {id}_{A^\vee }$ to ![]() $[P]$. This yields the desired result.
$[P]$. This yields the desired result.
Proposition 4.6 The morphism ![]() $h:H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))\to \operatorname {Hom}_{}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])$ is an injective morphism with image
$h:H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))\to \operatorname {Hom}_{}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])$ is an injective morphism with image ![]() $\operatorname {Hom}^{\mathrm {sym}}_{}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])$, the group of homomorphisms which are fixed by the involution
$\operatorname {Hom}^{\mathrm {sym}}_{}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])$, the group of homomorphisms which are fixed by the involution ![]() $\tau \mapsto \tau ^\vee$.
$\tau \mapsto \tau ^\vee$.
Proof. Suppose ![]() $\mathrm {char}(k)=p$ and write
$\mathrm {char}(k)=p$ and write ![]() $W$ for the ring of Witt vectors of
$W$ for the ring of Witt vectors of ![]() ${\bar {k}}$. The crystalline cohomology groups of an abelian variety are torsion free by [Reference Berthelot, Breen and MessingBBM82, Corollary 2.5.5]. Therefore, thanks to the Künneth formula, [Reference BerthelotBer74, Theorem V.4.2.1], we have that
${\bar {k}}$. The crystalline cohomology groups of an abelian variety are torsion free by [Reference Berthelot, Breen and MessingBBM82, Corollary 2.5.5]. Therefore, thanks to the Künneth formula, [Reference BerthelotBer74, Theorem V.4.2.1], we have that ![]() ${H^*_{{\mathrm {crys}}}(A_{\bar {k}}\times _{\bar {k}} A_{\bar {k}}/W)=H^*_{{\mathrm {crys}}}(A_{\bar {k}}/W)\otimes H^*_{{\mathrm {crys}}}(A_{\bar {k}}/W)}$ so that
${H^*_{{\mathrm {crys}}}(A_{\bar {k}}\times _{\bar {k}} A_{\bar {k}}/W)=H^*_{{\mathrm {crys}}}(A_{\bar {k}}/W)\otimes H^*_{{\mathrm {crys}}}(A_{\bar {k}}/W)}$ so that ![]() $m:A\times _k A\to A$ induces a morphism
$m:A\times _k A\to A$ induces a morphism
In degree ![]() $2$ we get a morphism
$2$ we get a morphism
which, in turn, induces a morphism
Write ![]() $\sigma : \bigwedge ^2 H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)\xrightarrow {\sim } H^2_{{\mathrm {crys}}}(A_{\bar {k}}/W)$ for the natural isomorphism induced by the cup product, as in [Reference Berthelot, Breen and MessingBBM82, Corollary 2.5.5]. For every
$\sigma : \bigwedge ^2 H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)\xrightarrow {\sim } H^2_{{\mathrm {crys}}}(A_{\bar {k}}/W)$ for the natural isomorphism induced by the cup product, as in [Reference Berthelot, Breen and MessingBBM82, Corollary 2.5.5]. For every ![]() $v\in H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)$, the pullback
$v\in H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)$, the pullback ![]() $m^*(v)$ is equal to
$m^*(v)$ is equal to ![]() $\pi _1^*(v)+\pi _2^*(v)$. Therefore, the composition
$\pi _1^*(v)+\pi _2^*(v)$. Therefore, the composition ![]() $(m^*-\pi _1^*-\pi _2^*)\circ \sigma : \bigwedge ^2 H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)\hookrightarrow H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)^{\otimes 2}$ is equal to the natural embedding
$(m^*-\pi _1^*-\pi _2^*)\circ \sigma : \bigwedge ^2 H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)\hookrightarrow H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)^{\otimes 2}$ is equal to the natural embedding ![]() $v\wedge w\mapsto v\otimes w- w\otimes v$. By [Reference Berthelot, Breen and MessingBBM82, Theorem 5.1.8], we have that the
$v\wedge w\mapsto v\otimes w- w\otimes v$. By [Reference Berthelot, Breen and MessingBBM82, Theorem 5.1.8], we have that the ![]() $F$-crystal
$F$-crystal ![]() $H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)$ over
$H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)$ over ![]() ${\bar {k}}$ is canonically isomorphic to
${\bar {k}}$ is canonically isomorphic to ![]() $H^1_{{\mathrm {crys}}}(A_{\bar {k}}^\vee /W)^\vee$ with
$H^1_{{\mathrm {crys}}}(A_{\bar {k}}^\vee /W)^\vee$ with ![]() $F$-structure defined as the dual of the
$F$-structure defined as the dual of the ![]() $F$-structure of
$F$-structure of ![]() $H^1_{{\mathrm {crys}}}(A_{\bar {k}}^\vee /W)$ multiplied by
$H^1_{{\mathrm {crys}}}(A_{\bar {k}}^\vee /W)$ multiplied by ![]() $p$. Thus, we have that
$p$. Thus, we have that
where ![]() $\mathbf {F\textbf {-}Crys}({\bar {k}})$ is the category of
$\mathbf {F\textbf {-}Crys}({\bar {k}})$ is the category of ![]() $F$-crystals over
$F$-crystals over ![]() ${\bar {k}}$. By [Reference IllusieIll79, Rmq. II.3.11.2], the
${\bar {k}}$. By [Reference IllusieIll79, Rmq. II.3.11.2], the ![]() $F$-crystals
$F$-crystals ![]() $H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)$ and
$H^1_{{\mathrm {crys}}}(A_{\bar {k}}/W)$ and ![]() $H^1_{{\mathrm {crys}}}(A_{\bar {k}}^\vee /W)$ are the contravariant crystalline Dieudonné modules of the
$H^1_{{\mathrm {crys}}}(A_{\bar {k}}^\vee /W)$ are the contravariant crystalline Dieudonné modules of the ![]() $p$-divisible groups
$p$-divisible groups ![]() $A_{\bar {k}}[p^\infty ]$ and
$A_{\bar {k}}[p^\infty ]$ and ![]() $A^\vee _{\bar {k}}[p^\infty ]$, thus we get
$A^\vee _{\bar {k}}[p^\infty ]$, thus we get
On the other hand, by [Reference IllusieIll79, Theorem II.5.14], there is a canonical isomorphism ![]() $H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))=H^2_{{\mathrm {crys}}}(A_{\bar {k}}/W)^{F=p}$. This concludes the case when
$H^2(A_{\bar {k}},{\mathbb {Z}_{p}}(1))=H^2_{{\mathrm {crys}}}(A_{\bar {k}}/W)^{F=p}$. This concludes the case when ![]() $\mathrm {char}(k)=p$. If
$\mathrm {char}(k)=p$. If ![]() $p$ is invertible in
$p$ is invertible in ![]() $k$ one can replace crystalline cohomology with
$k$ one can replace crystalline cohomology with ![]() $p$-adic étale cohomology.
$p$-adic étale cohomology.
5. Main results
We are now ready to prove our main result, which is a flat version of the Tate conjecture for divisors of abelian varieties.
Theorem 5.1 If ![]() $A$ is an abelian variety over a finitely generated field
$A$ is an abelian variety over a finitely generated field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$, then
$p>0$, then ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}})^k)=0$. Moreover, after possibly replacing
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}})^k)=0$. Moreover, after possibly replacing ![]() $k$ with a finite separable extension, the cycle class map
$k$ with a finite separable extension, the cycle class map
becomes an isomorphism.
Proof. To prove the statement we may assume that ![]() $\mathrm {Pic}(A)\to \mathrm {NS}(A_{{\bar {k}}})$ is surjective by extending
$\mathrm {Pic}(A)\to \mathrm {NS}(A_{{\bar {k}}})$ is surjective by extending ![]() $k$. The
$k$. The ![]() ${\mathbb {Z}_{p}}$-module
${\mathbb {Z}_{p}}$-module ![]() $\operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$ embeds into
$\operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$ embeds into ![]() $\operatorname {Hom}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])$, therefore the morphism
$\operatorname {Hom}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])$, therefore the morphism
induces a morphism ![]() $\tilde {h}:H^2(A_{\bar {k}},\mathbb {Z}_p(1))^{k}\to \operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$. By Proposition 4.6, we know that
$\tilde {h}:H^2(A_{\bar {k}},\mathbb {Z}_p(1))^{k}\to \operatorname {Hom}(A[p^\infty ],A^\vee [p^\infty ])$. By Proposition 4.6, we know that ![]() $\tilde {h}$ is injective and
$\tilde {h}$ is injective and ![]() $\mathrm {im}(\tilde {h})$ is contained in
$\mathrm {im}(\tilde {h})$ is contained in ![]() $\operatorname {Hom}^{\mathrm {sym}}(A[p^\infty ],A^\vee [p^\infty ])$. In addition, by Proposition 4.5, we have the following commutative square.
$\operatorname {Hom}^{\mathrm {sym}}(A[p^\infty ],A^\vee [p^\infty ])$. In addition, by Proposition 4.5, we have the following commutative square.

The lower arrow is an isomorphism by [Reference de JongdeJ98, Theorem 2.6], and since ![]() $\mathrm {NS}(A)=\operatorname {Hom}^{\mathrm {sym}}(A,A^\vee )$, we deduce that
$\mathrm {NS}(A)=\operatorname {Hom}^{\mathrm {sym}}(A,A^\vee )$, we deduce that ![]() $\mathrm {im}(\tilde {h}\circ c_1)=\operatorname {Hom}^{\mathrm {sym}}(A[p^\infty ],A^\vee [p^\infty ])$. This implies that
$\mathrm {im}(\tilde {h}\circ c_1)=\operatorname {Hom}^{\mathrm {sym}}(A[p^\infty ],A^\vee [p^\infty ])$. This implies that
is surjective, thus by Proposition 3.9 we get that
is surjective. Combining this with Proposition 3.8, we deduce that
is surjective. For the result about the Brauer group, we just note that by the previous argument and Proposition 3.8, the ![]() ${\mathbb {Z}_{p}}$-module
${\mathbb {Z}_{p}}$-module ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^k$ vanishes. Therefore, thanks to Proposition 3.9, we deduce that
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^k$ vanishes. Therefore, thanks to Proposition 3.9, we deduce that ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}})^k)=\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}})^k)[\frac {1}{p}]=0$.
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}})^k)=\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}})^k)[\frac {1}{p}]=0$.
Theorem 5.2 Let ![]() $A$ be an abelian variety over a finitely generated field
$A$ be an abelian variety over a finitely generated field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$. The transcendental Brauer group
$p>0$. The transcendental Brauer group ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}$ is a direct sum of a finite group and a finite exponent
$\mathrm {Br}(A_{{k_s}}\!)^{k}$ is a direct sum of a finite group and a finite exponent ![]() $p$-group. In addition, if the Witt vector cohomology group
$p$-group. In addition, if the Witt vector cohomology group ![]() $H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite
$H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite ![]() $W({\bar {k}})$-module, then
$W({\bar {k}})$-module, then ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}$ is finite.
$\mathrm {Br}(A_{{k_s}}\!)^{k}$ is finite.
Proof. By [Reference Colliot-Thélène and SkorobogatovCS21, Theorem 16.2.3], the group ![]() $\mathrm {Br}(A_{{k_s}}\!)^{k}[\frac {1}{p}]$ is finite. Moreover, thanks to Corollary 3.4, the morphism
$\mathrm {Br}(A_{{k_s}}\!)^{k}[\frac {1}{p}]$ is finite. Moreover, thanks to Corollary 3.4, the morphism ![]() $\mathrm {Br}(A_{{k_s}}\!)\to \mathrm {Br}(A_{{\bar {k}}})$ is injective, which implies that the transcendental Brauer group is the same as
$\mathrm {Br}(A_{{k_s}}\!)\to \mathrm {Br}(A_{{\bar {k}}})$ is injective, which implies that the transcendental Brauer group is the same as ![]() $\mathrm {Br}(A_{{\bar {k}}})^{k}$. Write
$\mathrm {Br}(A_{{\bar {k}}})^{k}$. Write ![]() $\mathbf {Ab}_p^\star \subseteq \mathbf {Ab}$ for the full subcategory of the category of abstract abelian groups with objects those (possibly infinite)
$\mathbf {Ab}_p^\star \subseteq \mathbf {Ab}$ for the full subcategory of the category of abstract abelian groups with objects those (possibly infinite) ![]() $p$-groups isomorphic to
$p$-groups isomorphic to ![]() $({\mathbb {Q}_{p}}/{\mathbb {Z}_{p}})^{\oplus a} \oplus M$ for some
$({\mathbb {Q}_{p}}/{\mathbb {Z}_{p}})^{\oplus a} \oplus M$ for some ![]() $a\geq 0$ and
$a\geq 0$ and ![]() $M$ a finite exponent
$M$ a finite exponent ![]() $p$-group. Equivalently,
$p$-group. Equivalently, ![]() $\mathbf {Ab}_p^\star$ is the subcategory of those
$\mathbf {Ab}_p^\star$ is the subcategory of those ![]() $p$-groups
$p$-groups ![]() $M$ such that
$M$ such that ![]() $M[p^{n+1}]/M[p^n]$ is finite for
$M[p^{n+1}]/M[p^n]$ is finite for ![]() $n$ big enough. Note that this subcategory is closed under the operation of taking subobjects, quotients, and finite direct sums. We first want to prove that
$n$ big enough. Note that this subcategory is closed under the operation of taking subobjects, quotients, and finite direct sums. We first want to prove that ![]() $H:=\varinjlim _n H^2(A_{\bar {k}},{\mu _{p^n}}\!)\in \mathbf {Ab}_p^\star$ and when
$H:=\varinjlim _n H^2(A_{\bar {k}},{\mu _{p^n}}\!)\in \mathbf {Ab}_p^\star$ and when ![]() $H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite
$H^2(A_{{\bar {k}}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite ![]() $W({\bar {k}})$-module then, in addition,
$W({\bar {k}})$-module then, in addition, ![]() $H[p]$ is finite (so that
$H[p]$ is finite (so that ![]() $H[p^n]$ is also finite for every
$H[p^n]$ is also finite for every ![]() $n\geq 0$). Thanks to the Kummer exact sequence this implies the same result for
$n\geq 0$). Thanks to the Kummer exact sequence this implies the same result for ![]() $\mathrm {Br}(A_{{\bar {k}}})^{k}[p^\infty ]$.
$\mathrm {Br}(A_{{\bar {k}}})^{k}[p^\infty ]$.
Write ![]() $q: A_{\bar {k}} \to \operatorname {Spec}({\bar {k}})$ for the structural morphism. By [Reference Bragg and OlssonBO21, Corollary 1.4], for every
$q: A_{\bar {k}} \to \operatorname {Spec}({\bar {k}})$ for the structural morphism. By [Reference Bragg and OlssonBO21, Corollary 1.4], for every ![]() $n$ there exists a commutative linear algebraic group
$n$ there exists a commutative linear algebraic group ![]() $G_n$ representing
$G_n$ representing ![]() $R^2q_{*}\mu _{p^n}$.Footnote 6 Write
$R^2q_{*}\mu _{p^n}$.Footnote 6 Write ![]() $U_n$ for the unipotent radical of
$U_n$ for the unipotent radical of ![]() $G_n$ and
$G_n$ and ![]() $D_n$ for the reductive quotient
$D_n$ for the reductive quotient ![]() $G_n/U_n$. Since
$G_n/U_n$. Since ![]() $G_n$ is commutative, there is a canonical Levi decomposition
$G_n$ is commutative, there is a canonical Levi decomposition ![]() $G_n=U_n\times D_n$. In particular, we have that
$G_n=U_n\times D_n$. In particular, we have that ![]() $H=U\times D$, where
$H=U\times D$, where ![]() $U:=\varinjlim _nU_n({\bar {k}})$ and
$U:=\varinjlim _nU_n({\bar {k}})$ and ![]() $D:=\varinjlim _nD_n({\bar {k}})$. For every
$D:=\varinjlim _nD_n({\bar {k}})$. For every ![]() $n>0$, the group scheme
$n>0$, the group scheme ![]() $D_n$ is finite, because it is a reductive group killed by
$D_n$ is finite, because it is a reductive group killed by ![]() $p^n$. In addition, by [Reference Bragg and OlssonBO21, Proposition 10.7], there is a canonical isomorphism of formal groups
$p^n$. In addition, by [Reference Bragg and OlssonBO21, Proposition 10.7], there is a canonical isomorphism of formal groups ![]() $\varinjlim _n \hat {G}_n=\varinjlim _n \hat {U}_n=\Phi ^2_{\mathrm {fl}}(A_{\bar {k}},\mathbb {G}_m)$, where
$\varinjlim _n \hat {G}_n=\varinjlim _n \hat {U}_n=\Phi ^2_{\mathrm {fl}}(A_{\bar {k}},\mathbb {G}_m)$, where ![]() $\hat {G}_n$ and
$\hat {G}_n$ and ![]() $\hat {U}_n$ are the formal completions at the identity of
$\hat {U}_n$ are the formal completions at the identity of ![]() $G_n$ and
$G_n$ and ![]() $U_n$ and
$U_n$ and ![]() $\Phi ^2_{\mathrm {fl}}(-,-)$ is as in [Reference Bragg and OlssonBO21, § 10.6].
$\Phi ^2_{\mathrm {fl}}(-,-)$ is as in [Reference Bragg and OlssonBO21, § 10.6].
Applying ![]() $Rq_*$ to the exact sequence
$Rq_*$ to the exact sequence
and using the fact that ![]() $\varinjlim _n R^1q_{*}\mu _{p^n}=\mathrm {Pic}_{A_{{\bar {k}}}/{\bar {k}}}[p^\infty ]$ is a
$\varinjlim _n R^1q_{*}\mu _{p^n}=\mathrm {Pic}_{A_{{\bar {k}}}/{\bar {k}}}[p^\infty ]$ is a ![]() $p$-divisible group, we get the exact sequence
$p$-divisible group, we get the exact sequence
As a first consequence, we deduce that for every ![]() $n>0$ the group scheme
$n>0$ the group scheme ![]() $D_n$ is the same as
$D_n$ is the same as ![]() $D_{n+1}[p^n]$, thus
$D_{n+1}[p^n]$, thus ![]() $D[p]=D_1({\bar {k}})$ is finite. In particular, the abstract group
$D[p]=D_1({\bar {k}})$ is finite. In particular, the abstract group ![]() $D$ is in
$D$ is in ![]() $\mathbf {Ab}_p^\star$. To bound
$\mathbf {Ab}_p^\star$. To bound ![]() $U$, we note that by [Reference MilneMil86, Proposition 3.1] the dimension of the chain of algebraic groups
$U$, we note that by [Reference MilneMil86, Proposition 3.1] the dimension of the chain of algebraic groups ![]() $G_1\subseteq G_2\subseteq \cdots$ is eventually constant. Therefore, there exists
$G_1\subseteq G_2\subseteq \cdots$ is eventually constant. Therefore, there exists ![]() $N>0$ such that for every
$N>0$ such that for every ![]() $n\geq N$, the morphism
$n\geq N$, the morphism ![]() $(U_n)_{\mathrm {red}}\to (U_{n+1})_{\mathrm {red}}$ is an isomorphism. This shows that
$(U_n)_{\mathrm {red}}\to (U_{n+1})_{\mathrm {red}}$ is an isomorphism. This shows that ![]() $U$ is a finite exponent
$U$ is a finite exponent ![]() $p$-group.
$p$-group.
If ![]() $H^2(A_{\bar {k}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite
$H^2(A_{\bar {k}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is a finite ![]() $W({\bar {k}})$-module, then the formal group
$W({\bar {k}})$-module, then the formal group ![]() $\Phi ^2_{\mathrm {fl}}(A_{\bar {k}},\mathbb {G}_m)$ does not contain any copy of
$\Phi ^2_{\mathrm {fl}}(A_{\bar {k}},\mathbb {G}_m)$ does not contain any copy of ![]() $\hat {\mathbb {G}}_a$. Indeed, by [Reference Bragg and OlssonBO21, Corollary 12.5], the group
$\hat {\mathbb {G}}_a$. Indeed, by [Reference Bragg and OlssonBO21, Corollary 12.5], the group ![]() $H^2(A_{\bar {k}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is the Cartier module of
$H^2(A_{\bar {k}},W\mathcal {O}_{A_{\bar {k}}}\!)$ is the Cartier module of ![]() $\Phi ^2_{\mathrm {fl}}(A_{\bar {k}},\mathbb {G}_m)$ and, by the assumption, it cannot contain
$\Phi ^2_{\mathrm {fl}}(A_{\bar {k}},\mathbb {G}_m)$ and, by the assumption, it cannot contain ![]() ${\bar {k}}[[V]]$, the Cartier module of
${\bar {k}}[[V]]$, the Cartier module of ![]() $\hat {\mathbb {G}}_a$. Therefore, in this case, we have that each group
$\hat {\mathbb {G}}_a$. Therefore, in this case, we have that each group ![]() $U_n({\bar {k}})$ is trivial, so that
$U_n({\bar {k}})$ is trivial, so that ![]() $H[p]=D[p]$ is finite.
$H[p]=D[p]$ is finite.
We can finally prove that ![]() $\mathrm {Br}(A_{{\bar {k}}})^{k}[p^\infty ]$ has finite exponent. Suppose by contradiction that this is not the case. Since
$\mathrm {Br}(A_{{\bar {k}}})^{k}[p^\infty ]$ has finite exponent. Suppose by contradiction that this is not the case. Since ![]() $\mathrm {Br}(A_{{\bar {k}}})^{k}[p^\infty ]\in \mathbf {Ab}_p^\star$, we deduce that it contains a copy of
$\mathrm {Br}(A_{{\bar {k}}})^{k}[p^\infty ]\in \mathbf {Ab}_p^\star$, we deduce that it contains a copy of ![]() ${\mathbb {Q}_{p}}/{\mathbb {Z}_{p}}$. On the other hand, by Theorem 5.1, the group
${\mathbb {Q}_{p}}/{\mathbb {Z}_{p}}$. On the other hand, by Theorem 5.1, the group ![]() $\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}})^{k})$ vanishes, which leads to a contradiction.
$\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}})^{k})$ vanishes, which leads to a contradiction.
Corollary 5.3 The group ![]() $\mathrm {Br}(A_{{k_s}}\!)^{\Gamma _k}$ has finite exponent.
$\mathrm {Br}(A_{{k_s}}\!)^{\Gamma _k}$ has finite exponent.
Proof. This follows from Theorem 5.2 thanks to [Reference Colliot-Thélène and SkorobogatovCS21, Theorem 5.4.12].
We end this section with some examples of abelian varieties over finitely generated fields with infinite transcendental Brauer group. Let ![]() $E$ be a supersingular elliptic curve over an infinite finitely generated field
$E$ be a supersingular elliptic curve over an infinite finitely generated field ![]() $k$ and let
$k$ and let ![]() $A$ be the product
$A$ be the product ![]() $E\times _k E$.
$E\times _k E$.
Proposition 5.4 After possibly extending ![]() $k$ to a finite separable extension, the transcendental Brauer group
$k$ to a finite separable extension, the transcendental Brauer group ![]() $\mathrm {Br}(A_{{k_s}}\!)^k$ becomes infinite.
$\mathrm {Br}(A_{{k_s}}\!)^k$ becomes infinite.
Proof. Even in this case we use that, thanks to Corollary 3.4, the transcendental Brauer group is the same as ![]() $\mathrm {Br}(A_{{\bar {k}}})^{k}$. Moreover, after extending the scalars we may assume that the morphism
$\mathrm {Br}(A_{{\bar {k}}})^{k}$. Moreover, after extending the scalars we may assume that the morphism ![]() $\mathrm {Pic}(A)\to \mathrm {NS}(A_{{\bar {k}}})$ is surjective. Combining Proposition 3.8 and the fact that
$\mathrm {Pic}(A)\to \mathrm {NS}(A_{{\bar {k}}})$ is surjective. Combining Proposition 3.8 and the fact that ![]() $\mathrm {NS}(A_{{\bar {k}}})/p$ is finite we deduce that it is enough to show that
$\mathrm {NS}(A_{{\bar {k}}})/p$ is finite we deduce that it is enough to show that ![]() $H^2(A_{{\bar {k}}},\mu _p)^k$ is infinite. We look at the Leray spectral sequence with respect to the second projection
$H^2(A_{{\bar {k}}},\mu _p)^k$ is infinite. We look at the Leray spectral sequence with respect to the second projection ![]() $\pi _2:A=E\times _k E\to E$ (both over
$\pi _2:A=E\times _k E\to E$ (both over ![]() $k$ and over
$k$ and over ![]() ${\bar {k}}$). In the second page, we have that the boundary morphism
${\bar {k}}$). In the second page, we have that the boundary morphism ![]() $H^1(E,R^1\pi _{2*} \mu _p) \to H^3 (E,\pi _{2*}\mu _p)$ vanishes because
$H^1(E,R^1\pi _{2*} \mu _p) \to H^3 (E,\pi _{2*}\mu _p)$ vanishes because ![]() $H^3 (E,\pi _{2*}\mu _p)\to H^3(A,\mu _p)$ admits a retraction induced by the zero section of
$H^3 (E,\pi _{2*}\mu _p)\to H^3(A,\mu _p)$ admits a retraction induced by the zero section of ![]() $\pi _2$. Since
$\pi _2$. Since ![]() $H^0(E_{\bar {k}},R^2\pi _{2*}\mu _p)=H^2(E_{\bar {k}},\mu _p)=\mathbb {Z}/p$, it is then enough to show that the image of
$H^0(E_{\bar {k}},R^2\pi _{2*}\mu _p)=H^2(E_{\bar {k}},\mu _p)=\mathbb {Z}/p$, it is then enough to show that the image of
is infinite. By Lemma 4.3, we have that ![]() $\operatorname {End}(E[p])$ (respectively,
$\operatorname {End}(E[p])$ (respectively, ![]() $\operatorname {End}(E_{{\bar {k}}}[p])$) admits a natural embedding in
$\operatorname {End}(E_{{\bar {k}}}[p])$) admits a natural embedding in ![]() $H^1(E,E[p])$ (respectively,
$H^1(E,E[p])$ (respectively, ![]() $H^1(E_{{\bar {k}}},E_{{\bar {k}}}[p])$). Since
$H^1(E_{{\bar {k}}},E_{{\bar {k}}}[p])$). Since
by the assumption that ![]() $E$ is supersingular, we deduce the desired result.
$E$ is supersingular, we deduce the desired result.
6. Specialisation of Néron–Severi groups
6.1
We want to start this section with an explicative example. Let ![]() $\mathcal {E}\to X$ be a non-isotrivial family of ordinary elliptic curves, where
$\mathcal {E}\to X$ be a non-isotrivial family of ordinary elliptic curves, where ![]() $X$ is a connected normal scheme of finite type over
$X$ is a connected normal scheme of finite type over ![]() $\mathbb {F}_p$. Let
$\mathbb {F}_p$. Let ![]() $\mathcal {A}$ be the fibred product
$\mathcal {A}$ be the fibred product ![]() $\mathcal {E}\times _X \mathcal {E}$. We denote by
$\mathcal {E}\times _X \mathcal {E}$. We denote by ![]() $E$ and
$E$ and ![]() $A$ the generic fibres over the generic point
$A$ the generic fibres over the generic point ![]() $\operatorname {Spec}(k)\hookrightarrow X$. The Kummer exact sequence induces the exact sequence
$\operatorname {Spec}(k)\hookrightarrow X$. The Kummer exact sequence induces the exact sequence
The group ![]() $\mathrm {NS}(A_{\bar {k}})_{\mathbb {Z}_p}$ is of rank
$\mathrm {NS}(A_{\bar {k}})_{\mathbb {Z}_p}$ is of rank ![]() $2+\operatorname {rk}_\mathbb {Z}(\operatorname {End}(E_{\bar {k}}))=3$, whereas, by Proposition 4.6, the rank of
$2+\operatorname {rk}_\mathbb {Z}(\operatorname {End}(E_{\bar {k}}))=3$, whereas, by Proposition 4.6, the rank of ![]() $H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ is
$H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ is ![]() $2+\operatorname {rk}_{\mathbb {Z}_{p}}(\operatorname {End}(E_{\bar {k}}[p^\infty ]))=4$. This shows that
$2+\operatorname {rk}_{\mathbb {Z}_{p}}(\operatorname {End}(E_{\bar {k}}[p^\infty ]))=4$. This shows that ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ is of rank
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))$ is of rank ![]() $1$. The endomorphisms of
$1$. The endomorphisms of ![]() $E_{{\bar {k}}}[p^\infty ]$ are all defined over
$E_{{\bar {k}}}[p^\infty ]$ are all defined over ![]() ${k_i}$, which implies that the action of
${k_i}$, which implies that the action of ![]() $\Gamma _k$ on
$\Gamma _k$ on ![]() $H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ is trivial. In particular, the morphism
$H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ is trivial. In particular, the morphism ![]() $\mathrm {NS}(A)_{\mathbb {Z}_p} \to H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))^{\Gamma _k}$ is not surjective and the cokernel
$\mathrm {NS}(A)_{\mathbb {Z}_p} \to H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))^{\Gamma _k}$ is not surjective and the cokernel ![]() $\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}$ is isomorphic to
$\mathrm {T}_p(\mathrm {Br}(A_{\bar {k}}))^{\Gamma _k}$ is isomorphic to ![]() ${\mathbb {Z}_{p}}$.
${\mathbb {Z}_{p}}$.
In this case, the Galois action on ![]() $H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ is not enough to detect what classes are
$H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ is not enough to detect what classes are ![]() ${\mathbb {Z}_{p}}$-linear combinations of algebraic cycles. There is an additional obstruction to descend cohomology classes through the purely inseparable extension
${\mathbb {Z}_{p}}$-linear combinations of algebraic cycles. There is an additional obstruction to descend cohomology classes through the purely inseparable extension ![]() ${k_i}/k$. This extra purely inseparable obstruction gives an explanation of the failure of surjectivity of specialisation morphisms of Néron–Severi groups. In the example, if
${k_i}/k$. This extra purely inseparable obstruction gives an explanation of the failure of surjectivity of specialisation morphisms of Néron–Severi groups. In the example, if ![]() $\operatorname {Spec}(\kappa )\hookrightarrow X$ is a closed point, we have that
$\operatorname {Spec}(\kappa )\hookrightarrow X$ is a closed point, we have that ![]() $\mathrm {NS}(\mathcal {A}_{\kappa })=\mathrm {NS}(\mathcal {A}_{\bar {\kappa }})$ is of rank
$\mathrm {NS}(\mathcal {A}_{\kappa })=\mathrm {NS}(\mathcal {A}_{\bar {\kappa }})$ is of rank ![]() $4$ because
$4$ because ![]() $\operatorname {End}(\mathcal {E}_\kappa )=\operatorname {End}(\mathcal {E}_{\bar \kappa })$ is of rank
$\operatorname {End}(\mathcal {E}_\kappa )=\operatorname {End}(\mathcal {E}_{\bar \kappa })$ is of rank ![]() $2$ (there is an extra Frobenius endomorphism). Thus, the specialisation map
$2$ (there is an extra Frobenius endomorphism). Thus, the specialisation map ![]() $\mathrm {NS}(A)\hookrightarrow \mathrm {NS}(\mathcal {A}_\kappa )$ is never surjective even if the rank of
$\mathrm {NS}(A)\hookrightarrow \mathrm {NS}(\mathcal {A}_\kappa )$ is never surjective even if the rank of ![]() $H^2_{}(A_{\bar {\kappa }},\mathbb {Z}_p(1))$ is
$H^2_{}(A_{\bar {\kappa }},\mathbb {Z}_p(1))$ is ![]() $4$ as the generic geometric fibre and the Galois action is trivial in both cases. One can interpret this failure by saying that the extra obstruction on
$4$ as the generic geometric fibre and the Galois action is trivial in both cases. One can interpret this failure by saying that the extra obstruction on ![]() $H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ coming from the purely inseparable extension
$H^2_{}(A_{\bar {k}},\mathbb {Z}_p(1))$ coming from the purely inseparable extension ![]() ${k_i}/k$ is trivial on
${k_i}/k$ is trivial on ![]() $H^2_{}(A_{\bar {\kappa }},\mathbb {Z}_p(1))$ since
$H^2_{}(A_{\bar {\kappa }},\mathbb {Z}_p(1))$ since ![]() $\kappa$ is perfect. In general, we prove the following theorem.
$\kappa$ is perfect. In general, we prove the following theorem.
Theorem 6.2 Let ![]() $X$ be a connected normal scheme of finite type over
$X$ be a connected normal scheme of finite type over ![]() $\mathbb {F}_p$ with generic point
$\mathbb {F}_p$ with generic point ![]() $\eta =\operatorname {Spec}(k)$ and let
$\eta =\operatorname {Spec}(k)$ and let ![]() $f:\mathcal {A}\to X$ be an abelian scheme over
$f:\mathcal {A}\to X$ be an abelian scheme over ![]() $X$ with constant Newton polygon. For every closed point
$X$ with constant Newton polygon. For every closed point ![]() $x=\operatorname {Spec}(\kappa )$ of
$x=\operatorname {Spec}(\kappa )$ of ![]() $X$ we have
$X$ we have
Remark 6.3 Note that after replacing ![]() $X$ with a finite étale cover the action of
$X$ with a finite étale cover the action of ![]() $\Gamma _k$ on
$\Gamma _k$ on ![]() $\mathrm {NS}(\mathcal {A}_{\bar {\eta }})$ is trivial. Thus, we also get an inequality before taking Galois-fixed points.
$\mathrm {NS}(\mathcal {A}_{\bar {\eta }})$ is trivial. Thus, we also get an inequality before taking Galois-fixed points.
To prove Theorem 6.2 we first need the following result.
Proposition 6.4 Under the assumptions of Theorem 6.2, the functor ![]() $\mathcal {F}$ which sendsFootnote 7
$\mathcal {F}$ which sendsFootnote 7 ![]() $T\in (X^{\mathrm {perf}})_{\mathrm {pro}\mathrm {\acute {e}t}}$ to
$T\in (X^{\mathrm {perf}})_{\mathrm {pro}\mathrm {\acute {e}t}}$ to ![]() $\operatorname {Hom}^{{\mathrm {sym}}}(\mathcal {A}_T[p^\infty ],\mathcal {A}^\vee _T[p^\infty ])[\frac {1}{p}]$ is a semi-simple finite-rank
$\operatorname {Hom}^{{\mathrm {sym}}}(\mathcal {A}_T[p^\infty ],\mathcal {A}^\vee _T[p^\infty ])[\frac {1}{p}]$ is a semi-simple finite-rank ![]() ${\mathbb {Q}_{p}}$-local system such that for every
${\mathbb {Q}_{p}}$-local system such that for every ![]() $\bar {x}\in X(\bar {\mathbb {F}}_p)$ we have
$\bar {x}\in X(\bar {\mathbb {F}}_p)$ we have
Proof. Let ![]() $\widetilde {\mathcal {F}}$ be the functor which sends
$\widetilde {\mathcal {F}}$ be the functor which sends ![]() $T\in (X^{\mathrm {perf}})_{\mathrm {pro}\mathrm {\acute {e}t}}$ to
$T\in (X^{\mathrm {perf}})_{\mathrm {pro}\mathrm {\acute {e}t}}$ to ![]() $\operatorname {Hom}(\mathcal {A}_T[p^\infty ],\mathcal {A}^\vee _T[p^\infty ])[\frac {1}{p}]$. We first note that to prove the result we can replace
$\operatorname {Hom}(\mathcal {A}_T[p^\infty ],\mathcal {A}^\vee _T[p^\infty ])[\frac {1}{p}]$. We first note that to prove the result we can replace ![]() $\mathcal {F}$ with
$\mathcal {F}$ with ![]() $\widetilde {\mathcal {F}}$ since
$\widetilde {\mathcal {F}}$ since ![]() $\mathcal {F}$ is the kernel of the
$\mathcal {F}$ is the kernel of the ![]() ${\mathbb {Q}_{p}}$-linear endomorphism
${\mathbb {Q}_{p}}$-linear endomorphism ![]() $\alpha -\operatorname {id}_{\widetilde {\mathcal {F}}}:\widetilde {\mathcal {F}}\to \widetilde {\mathcal {F}}$ where
$\alpha -\operatorname {id}_{\widetilde {\mathcal {F}}}:\widetilde {\mathcal {F}}\to \widetilde {\mathcal {F}}$ where ![]() $\alpha$ sends
$\alpha$ sends ![]() $\tau \in \operatorname {Hom}(\mathcal {A}_T[p^\infty ],\mathcal {A}^\vee _T[p^\infty ])[\frac {1}{p}]$ to
$\tau \in \operatorname {Hom}(\mathcal {A}_T[p^\infty ],\mathcal {A}^\vee _T[p^\infty ])[\frac {1}{p}]$ to ![]() $\tau ^\vee$. Write
$\tau ^\vee$. Write ![]() $\mathbf {F\textrm {-}Crys}(X)$ for the category of
$\mathbf {F\textrm {-}Crys}(X)$ for the category of ![]() $F$-crystals over the absolute crystalline site of
$F$-crystals over the absolute crystalline site of ![]() $X$ and let
$X$ and let ![]() $\mathcal {M}_1,\mathcal {M}_2\in \mathbf {F\textrm {-}Crys}(X)$ be the contravariant crystalline Dieudonné modules of
$\mathcal {M}_1,\mathcal {M}_2\in \mathbf {F\textrm {-}Crys}(X)$ be the contravariant crystalline Dieudonné modules of ![]() $\mathcal {A}[p^\infty ]$ and
$\mathcal {A}[p^\infty ]$ and ![]() $\mathcal {A}^\vee [p^\infty ]$ over
$\mathcal {A}^\vee [p^\infty ]$ over ![]() $X$ constructed in [Reference Berthelot, Breen and MessingBBM82, Déf. 3.3.6]. By [Reference Berthelot, Breen and MessingBBM82, Theorem 5.1.8], we have that
$X$ constructed in [Reference Berthelot, Breen and MessingBBM82, Déf. 3.3.6]. By [Reference Berthelot, Breen and MessingBBM82, Theorem 5.1.8], we have that ![]() $\mathcal {M}_1= \mathcal {M}_2^\vee (-1)$ where
$\mathcal {M}_1= \mathcal {M}_2^\vee (-1)$ where ![]() $\mathcal {M}_2^\vee (-1)$ is the
$\mathcal {M}_2^\vee (-1)$ is the ![]() $F$-crystal
$F$-crystal ![]() $\mathcal {H}om(\mathcal {M}_2,\mathcal {O}_{X,\mathrm {cris}})$ endowed with the dual of the
$\mathcal {H}om(\mathcal {M}_2,\mathcal {O}_{X,\mathrm {cris}})$ endowed with the dual of the ![]() $F$-structure of
$F$-structure of ![]() $\mathcal {M}_2$ multiplied by
$\mathcal {M}_2$ multiplied by ![]() $p$. Thus
$p$. Thus ![]() $\mathcal {M}_1^{\otimes 2}$ is equal to
$\mathcal {M}_1^{\otimes 2}$ is equal to ![]() $\mathcal {H}om(\mathcal {M}_2,\mathcal {M}_1)$ endowed with the natural
$\mathcal {H}om(\mathcal {M}_2,\mathcal {M}_1)$ endowed with the natural ![]() $F$-structure multiplied by
$F$-structure multiplied by ![]() $p$. By [Reference LauLau13, Theorem D], for every perfect scheme
$p$. By [Reference LauLau13, Theorem D], for every perfect scheme ![]() $T\to X$ we have canonical isomorphisms
$T\to X$ we have canonical isomorphisms
where ![]() $\mathcal {M}_{1,T}$ and
$\mathcal {M}_{1,T}$ and ![]() $\mathcal {M}_{2,T}$ are the inverse images of
$\mathcal {M}_{2,T}$ are the inverse images of ![]() $\mathcal {M}_1$ and
$\mathcal {M}_1$ and ![]() $\mathcal {M}_2$ to
$\mathcal {M}_2$ to ![]() $T$. These isomorphisms are equivariant with respect to the action of the abstract group
$T$. These isomorphisms are equivariant with respect to the action of the abstract group ![]() $\operatorname {Aut}(T/X)$.
$\operatorname {Aut}(T/X)$.
By [Reference KatzKat79, Theorem 2.5.1], the slope filtration of the ![]() $F$-crystal
$F$-crystal ![]() $\mathcal {M}_{1,X^{\textrm {perf}}}^{\otimes 2}$ (which exists since
$\mathcal {M}_{1,X^{\textrm {perf}}}^{\otimes 2}$ (which exists since ![]() $\mathcal {A}\to X$ has constant Newton polygon) splits uniquely up to isogeny. We denote by
$\mathcal {A}\to X$ has constant Newton polygon) splits uniquely up to isogeny. We denote by ![]() $\mathcal {N}^{[1]}_{X^\textrm {perf}}$ the slope
$\mathcal {N}^{[1]}_{X^\textrm {perf}}$ the slope ![]() $1$ subobject of
$1$ subobject of ![]() $\mathcal {M}_{1,X^{\textrm {perf}}}^{\otimes 2}$, defined up to isogeny. Note that for every
$\mathcal {M}_{1,X^{\textrm {perf}}}^{\otimes 2}$, defined up to isogeny. Note that for every ![]() $T\to X^\textrm {perf}$ we have that
$T\to X^\textrm {perf}$ we have that
By construction, the ![]() $F$-crystal
$F$-crystal ![]() $\mathcal {N}^{[1]}_{X^{\textrm {perf}}}(1)$ is unit-root. Therefore, by [Reference KatzKat73, Proposition 4.1.1], we deduce that
$\mathcal {N}^{[1]}_{X^{\textrm {perf}}}(1)$ is unit-root. Therefore, by [Reference KatzKat73, Proposition 4.1.1], we deduce that ![]() $\widetilde {\mathcal {F}}$ is a
$\widetilde {\mathcal {F}}$ is a ![]() ${\mathbb {Q}_{p}}$-local system. In addition, by [Reference KatzKat73, Lemma 4.3.15], for every
${\mathbb {Q}_{p}}$-local system. In addition, by [Reference KatzKat73, Lemma 4.3.15], for every ![]() $S=\operatorname {Spec}(R)\to X$ with
$S=\operatorname {Spec}(R)\to X$ with ![]() $R$ strictly henselian perfect ring we have
$R$ strictly henselian perfect ring we have
where ![]() $s$ is the closed point of
$s$ is the closed point of ![]() $S$. This implies that for every
$S$. This implies that for every ![]() $\bar {x}\in X(\bar {\mathbb {F}}_p)$ we have
$\bar {x}\in X(\bar {\mathbb {F}}_p)$ we have
For the semi-simplicity, since ![]() $X$ is normal, we can shrink
$X$ is normal, we can shrink ![]() $X$ and assume it smooth. Write
$X$ and assume it smooth. Write ![]() $\mathcal {N}$ for the
$\mathcal {N}$ for the ![]() $F$-isocrystal
$F$-isocrystal ![]() $(R^1f_{{\mathrm {crys}}*}\mathcal {O}_{\mathcal {A},{\mathrm {crys}}})^{\otimes 2}$ and
$(R^1f_{{\mathrm {crys}}*}\mathcal {O}_{\mathcal {A},{\mathrm {crys}}})^{\otimes 2}$ and ![]() $\mathcal {N}^{[1]}$ for the quotient
$\mathcal {N}^{[1]}$ for the quotient ![]() $\mathcal {N}^{\leq 1}/\mathcal {N}^{<1}$, where
$\mathcal {N}^{\leq 1}/\mathcal {N}^{<1}$, where ![]() $\mathcal {N}^{\leq 1}$ (respectively,
$\mathcal {N}^{\leq 1}$ (respectively, ![]() $\mathcal {N}^{<1}$) is the subobject of
$\mathcal {N}^{<1}$) is the subobject of ![]() $\mathcal {N}$ of slopes
$\mathcal {N}$ of slopes ![]() $\leq 1$ (respectively,
$\leq 1$ (respectively, ![]() $<1$). Note that by [Reference Berthelot, Breen and MessingBBM82, Theorem 2.5.6(ii)], the pullback of
$<1$). Note that by [Reference Berthelot, Breen and MessingBBM82, Theorem 2.5.6(ii)], the pullback of ![]() $\mathcal {N}^{[1]}$ to
$\mathcal {N}^{[1]}$ to ![]() $X^{\mathrm {perf}}$ is isomorphic as an
$X^{\mathrm {perf}}$ is isomorphic as an ![]() $F$-isocrystal with
$F$-isocrystal with ![]() $\mathcal {N}^{[1]}_{X^\textrm {perf}}$ over
$\mathcal {N}^{[1]}_{X^\textrm {perf}}$ over ![]() $X^{\textrm {perf}}$ defined above. Thanks to [Reference D'AddezioD'Ad23, Theorem 1.1.2], we have that
$X^{\textrm {perf}}$ defined above. Thanks to [Reference D'AddezioD'Ad23, Theorem 1.1.2], we have that ![]() $\mathcal {N}^{[1]}$ is semi-simple as an
$\mathcal {N}^{[1]}$ is semi-simple as an ![]() $F$-isocrystal.
$F$-isocrystal.
By [Reference CrewCre87, Theorem 2.1], there is an equivalence between unit-root ![]() $F$-isocrystals over
$F$-isocrystals over ![]() $X$ and finite-rank
$X$ and finite-rank ![]() ${\mathbb {Q}_{p}}$-local systems. By construction, Crew's and Katz's correspondences are compatible, in the sense that they agree after pulling back the objects through
${\mathbb {Q}_{p}}$-local systems. By construction, Crew's and Katz's correspondences are compatible, in the sense that they agree after pulling back the objects through ![]() $X^\mathrm {perf}\to X$. Since the étale fundamental groups of
$X^\mathrm {perf}\to X$. Since the étale fundamental groups of ![]() $X$ and
$X$ and ![]() $X^{\mathrm {perf}}$ are canonically isomorphic, we deduce that
$X^{\mathrm {perf}}$ are canonically isomorphic, we deduce that ![]() $\widetilde {\mathcal {F}}$ is semi-simple as well. This yields the desired result.
$\widetilde {\mathcal {F}}$ is semi-simple as well. This yields the desired result.
6.5
Proof of Theorem 6.2 We look at the exact sequence
Thanks to Proposition 6.4, the operation of taking Galois-fixed points is exact. We get the exact sequence
Looking at the ranks we deduce the following equality
By Proposition 6.4, the action of ![]() $\Gamma _k$ on
$\Gamma _k$ on ![]() $H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))=\operatorname {Hom}^{\mathrm {sym}}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])[\frac {1}{p}]$ factors through the étale fundamental group of
$H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))=\operatorname {Hom}^{\mathrm {sym}}(A_{\bar {k}}[p^\infty ],A^\vee _{\bar {k}}[p^\infty ])[\frac {1}{p}]$ factors through the étale fundamental group of ![]() $X$ associated to
$X$ associated to ![]() $\bar {\eta }$, denoted by
$\bar {\eta }$, denoted by ![]() $\pi _1^{\mathrm {\acute {e}t}}(X,\bar {\eta })$. In addition, if
$\pi _1^{\mathrm {\acute {e}t}}(X,\bar {\eta })$. In addition, if ![]() $\kappa$ is the residue field of
$\kappa$ is the residue field of ![]() $x$, the inclusion
$x$, the inclusion ![]() $x\hookrightarrow X$ induces then an action of
$x\hookrightarrow X$ induces then an action of ![]() $\Gamma _\kappa$ on
$\Gamma _\kappa$ on ![]() $H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))$ which corresponds, up to conjugation, to the action of
$H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))$ which corresponds, up to conjugation, to the action of ![]() $\Gamma _\kappa$ on
$\Gamma _\kappa$ on ![]() $H^2(A_{\bar {\kappa }},{\mathbb {Q}_{p}}(1))$. Therefore, by the Tate conjecture over finite fields (or Corollary 5.3), we get
$H^2(A_{\bar {\kappa }},{\mathbb {Q}_{p}}(1))$. Therefore, by the Tate conjecture over finite fields (or Corollary 5.3), we get ![]() $\mathrm {NS}(\mathcal {A}_{\bar {x}})^{\Gamma _\kappa }_{\mathbb {Q}_{p}}=H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))^{\Gamma _\kappa }$. Since
$\mathrm {NS}(\mathcal {A}_{\bar {x}})^{\Gamma _\kappa }_{\mathbb {Q}_{p}}=H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))^{\Gamma _\kappa }$. Since ![]() $H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))^{\Gamma _k}$ is a subspace of
$H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))^{\Gamma _k}$ is a subspace of ![]() $H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))^{\Gamma _\kappa }$ we deduce that
$H^2(A_{{\bar {k}}},{\mathbb {Q}_{p}}(1))^{\Gamma _\kappa }$ we deduce that
We want to conclude this section with other examples of abelian varieties such that ![]() $\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}}))^{\Gamma _k}\neq 0$. These are variants of the abelian surface of § 6.1 and they all provide counterexamples to the conjecture in [Reference UlmerUlm14, § 7.3.1] when
$\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}}))^{\Gamma _k}\neq 0$. These are variants of the abelian surface of § 6.1 and they all provide counterexamples to the conjecture in [Reference UlmerUlm14, § 7.3.1] when ![]() $\ell =p$.
$\ell =p$.
Proposition 6.6 Let ![]() $A$ be an abelian variety which splits as a product
$A$ be an abelian variety which splits as a product ![]() $B\times _k B$ with
$B\times _k B$ with ![]() $B$ an abelian variety over
$B$ an abelian variety over ![]() $k$. There is a natural exact sequence
$k$. There is a natural exact sequence
Proof. We consider the exact sequence
Arguing as in the proof of Proposition 4.6, the ![]() ${\mathbb {Z}_{p}}$-module
${\mathbb {Z}_{p}}$-module ![]() $\operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])^{\Gamma _k}$ is naturally a direct summand of
$\operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])^{\Gamma _k}$ is naturally a direct summand of ![]() $H^2(A_{{\bar {k}}}, {\mathbb {Z}_{p}}(1))^{\Gamma _k}$. Its preimage in
$H^2(A_{{\bar {k}}}, {\mathbb {Z}_{p}}(1))^{\Gamma _k}$. Its preimage in ![]() $\mathrm {NS}(A_{{\bar {k}}})_{\mathbb {Z}_{p}}^{\Gamma _k}$ corresponds to the
$\mathrm {NS}(A_{{\bar {k}}})_{\mathbb {Z}_{p}}^{\Gamma _k}$ corresponds to the ![]() ${\mathbb {Z}_{p}}$-module
${\mathbb {Z}_{p}}$-module
This concludes the proof.
Corollary 6.7 If ![]() $\operatorname {End}(B)=\mathbb {Z}$, then
$\operatorname {End}(B)=\mathbb {Z}$, then ![]() $\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}}))^{\Gamma _k}\neq 0$.
$\mathrm {T}_p(\mathrm {Br}(A_{{\bar {k}}}))^{\Gamma _k}\neq 0$.
Proof. By the assumption, ![]() $\operatorname {Hom}(B,B^\vee )_{\mathbb {Z}_{p}}$ is a
$\operatorname {Hom}(B,B^\vee )_{\mathbb {Z}_{p}}$ is a ![]() ${\mathbb {Z}_{p}}$-module of rank
${\mathbb {Z}_{p}}$-module of rank ![]() $1$. Therefore, by Proposition 6.6, it is enough to prove that the rank of
$1$. Therefore, by Proposition 6.6, it is enough to prove that the rank of ![]() $\operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])^{\Gamma _k}$ is greater than
$\operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])^{\Gamma _k}$ is greater than ![]() $1$. Since
$1$. Since ![]() $\operatorname {End}(B)=\mathbb {Z}$, the abelian variety
$\operatorname {End}(B)=\mathbb {Z}$, the abelian variety ![]() $B$ is not supersingular, so that the
$B$ is not supersingular, so that the ![]() $p$-divisible group
$p$-divisible group ![]() $B[p^\infty ]$ admits at least two slopes. By the Dieudonné–Manin classification, this implies that
$B[p^\infty ]$ admits at least two slopes. By the Dieudonné–Manin classification, this implies that ![]() $B_{{k_i}}[p^\infty ]$ is isogenous to a direct sum
$B_{{k_i}}[p^\infty ]$ is isogenous to a direct sum ![]() $\mathcal {G}_1\oplus \mathcal {G}_2$ of non-zero
$\mathcal {G}_1\oplus \mathcal {G}_2$ of non-zero ![]() $p$-divisible groups over
$p$-divisible groups over ![]() ${k_i}$. Since
${k_i}$. Since ![]() $\operatorname {End}(\mathcal {G}_1)[\frac {1}{p}]\oplus \operatorname {End}(\mathcal {G}_2)[\frac {1}{p}]$ embeds into
$\operatorname {End}(\mathcal {G}_1)[\frac {1}{p}]\oplus \operatorname {End}(\mathcal {G}_2)[\frac {1}{p}]$ embeds into ![]() $\operatorname {End}(B_{{k_i}}[p^\infty ])[\frac {1}{p}]\simeq \operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])[\frac {1}{p}]^{\Gamma _k}$, we deduce that
$\operatorname {End}(B_{{k_i}}[p^\infty ])[\frac {1}{p}]\simeq \operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])[\frac {1}{p}]^{\Gamma _k}$, we deduce that ![]() $\operatorname {rk}_{\mathbb {Z}_{p}}(\operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])^{\Gamma _k})>1$, as we wanted.
$\operatorname {rk}_{\mathbb {Z}_{p}}(\operatorname {Hom}(B_{\bar {k}}[p^\infty ],B_{\bar {k}}^\vee [p^\infty ])^{\Gamma _k})>1$, as we wanted.
Acknowledgements
I thank Emiliano Ambrosi for the discussions we had during the writing of [Reference Ambrosi and D'AddezioAD22], which inspired this article, Matthew Morrow and Kay Rülling for many enlightening conversations about the cohomology of ![]() $\mathbb {Z}_p(1)$, and Ofer Gabber, Luc Illusie, Peter Scholze, and Takashi Suzuki for answering some questions on the fppf site. I also thank Jean-Louis Colliot-Thélène, Bruno Kahn, Alexei Skorobogatov, and Takashi Suzuki for very useful comments on a first draft of this article. Finally, I thank the anonymous referees for their careful reading of the article and for the corrections they suggested.
$\mathbb {Z}_p(1)$, and Ofer Gabber, Luc Illusie, Peter Scholze, and Takashi Suzuki for answering some questions on the fppf site. I also thank Jean-Louis Colliot-Thélène, Bruno Kahn, Alexei Skorobogatov, and Takashi Suzuki for very useful comments on a first draft of this article. Finally, I thank the anonymous referees for their careful reading of the article and for the corrections they suggested.
The author was funded by the Deutsche Forschungsgemeinschaft (EXC-2046/1, project ID 390685689 and DA-2534/1-1, project ID 461915680) and by the Max-Planck Institute for Mathematics.
Conflicts of Interest
None.