Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T06:01:58.906Z Has data issue: false hasContentIssue false
  • English
  • Français

Bordered Floer homology and existence of incompressible tori in homology spheres

Part of: Low-dimensional topology Differential topology

Published online by Cambridge University Press:  18 May 2018

Eaman Eftekhary
Eaman Eftekhary*
Affiliation:
School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P. O. Box 19395-5746, Tehran, Iran email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

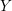Let $Y$ be a homology sphere which contains an incompressible torus. We show that 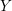$Y$ cannot be an 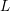$L$-space, i.e. the rank of 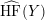$\widehat{\text{HF}}(Y)$ is greater than 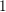$1$. In fact, if the homology sphere 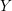$Y$ is an irreducible 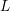$L$-space, then 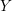$Y$ is 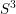$S^{3}$, the Poincaré sphere 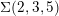$\unicode[STIX]{x1D6F4}(2,3,5)$ or hyperbolic.

Keywords

Floer homologysplicingincompressible torus

MSC classification

Primary: 57M27: Invariants of knots and 3-manifolds 57R58: Floer homology
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 6 , June 2018 , pp. 1222 - 1268
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alishahi, A. S. and Eftekhary, E., A refinement of sutured Floer homology , J. Symplectic Geom. 13 (2015), 609–743.Google Scholar
Bleiler, S. A., Knots prime on many strings , Trans. Amer. Math. Soc. 282(1) (1984), 385–401.Google Scholar
Boileau, M. and Boyer, S., Graph manifold ℤ-homology 3-spheres and taut foliations , J. Topol. 8 (2015), 571–585.CrossRefGoogle Scholar
Boileau, M. and Porti, J., Geometrization of 3-orbifolds of cyclic type, Astérisque, vol. 272 (Société Mathématique de France, Paris, 2001).Google Scholar
Cooper, D., Hodgson, C. D. and Kerckhoff, S. P., Three-dimensional orbifolds and cone manifolds, MSJ Memoirs, vol. 5 (Mathematical Society of Japan, Tokyo, 2000).Google Scholar
Eftekhary, E., Longitude Floer homology for knots and the Whitehead double , Algebr. Geom. Topol. 5 (2005), 1389–1418.Google Scholar
Eftekhary, E., Seifert fibered homology spheres with trivial Heegaard Floer homology, Preprint (2009), arXiv:0909.3975 [math.GT].Google Scholar
Eftekhary, E., Floer homology and splicing knot complements , Algebr. Geom. Topol. 15 (2015), 3155–3213.Google Scholar
Eftekhary, E., Correction to the article: Floer homology and splicing knot complements, Preprint (2017), arXiv:1710.10417 [math.GT].Google Scholar
Hedden, M. and Levine, A. S., Splicing knot complements and bordered Floer homology , J. reine angew. Math. 720 (2016), 129–154.Google Scholar
Hedden, M. and Watson, L., Does Khovanov homology detect the unknot? Amer. J. Math. 132 (2010), 1339–1345.Google Scholar
Hendricks, K. and Manolescu, C., Involutive Heegaard Floer homology, Preprint (2015),arXiv:1507.00383.Google Scholar
Kronheimer, P. B. and Mrowka, T. S., Khovanov homology is an unknot-detector , Publ. Math. Inst. Hautes Études Sci. 113 (2011), 97–208.Google Scholar
Lipshitz, R., Ozsvath, O. and Thurston, D., Bordered Heegaard Floer homology: invariance and pairing, Preprint (2008), arXiv:0810.0687.Google Scholar
Lipshitz, R., Ozsvath, O. and Thurston, D., Notes on bordered Floer homology , in Contact and symplectic topology, Bolyai Society Mathematical Studies, vol. 26 (János Bolyai Mathematical Society, Budapest, 2014), 275–355.CrossRefGoogle Scholar
Morgan, J. W. and Tian, G., Ricci flow and the Poincaré conjecture, Clay Mathematics Monographs, vol. 3 (American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2007).Google Scholar
Morgan, J. W. and Tian, G., The geometrization conjecture, Clay Mathematics Monographs, vol. 5 (American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2014).Google Scholar
Ni, Y., Link Floer homology detects Thurston norm , Geom. Topol. 13 (2009), 2991–3019.Google Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and topological invariants for closed three-manifolds , Ann. of Math. (2) 159 (2004), 1027–1158.Google Scholar
Ozsváth, P. and Szabó, Z., Holomorphic disks and knot invariants , Adv. Math. 189 (2004), 58–116.Google Scholar
Ozsváth, P. and Szabó, Z., On Heegaard Floer homology of branched double-covers , Adv. Math. 194 (2005), 1–33.Google Scholar
Ozsváth, P. and Szabó, Z., Knot Floer homology and integer surgeries , Algebr. Geom. Topol. 8 (2008), 101–153.Google Scholar
Perelman, G., Ricci flow with surgery on three-manifolds, Preprint (2003), arXiv:math/0307245 [math.DG].Google Scholar
Rolfsen, D., Knots and links, Mathematical Lecture Series, vol. 7 (Publish or Perish, Berkeley, CA, 1976).Google Scholar
Rustamov, R., On Heegaard Floer homology of plumbed three-manifolds with $b_{1}=1$ , Preprint (2004), arXiv:math/0405118 [math.SG].Google Scholar
Sarkar, S., Moving basepoints and the induced automorphisms of link Floer homology , Algebr. Geom. Topol. 15 (2015), 2479–2515.Google Scholar
Shumakovitch, A., KhoHo – a program for computing and studying Khovanov homology,http://www.geometrie.ch/KhoHo.Google Scholar
Thurston, W. P., Three-dimensional manifolds, Kleinian groups and hyperbolic geometry , Bull. Amer. Math. Soc. (N.S.) 6 (1982), 357–381.Google Scholar
Vafaee, F., Seifert surfaces distinguished by sutured Floer homology but not its Euler characteristic , Topology Appl. 184 (2015), 72–86.Google Scholar