Article contents
The Balmer spectrum of certain Deligne–Mumford stacks
Published online by Cambridge University Press: 24 May 2023
Abstract
We consider a Deligne–Mumford stack 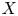 $X$ which is the quotient of an affine scheme
$X$ which is the quotient of an affine scheme 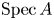 $\operatorname {Spec}A$ by the action of a finite group
$\operatorname {Spec}A$ by the action of a finite group 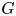 $G$ and show that the Balmer spectrum of the tensor triangulated category of perfect complexes on
$G$ and show that the Balmer spectrum of the tensor triangulated category of perfect complexes on 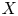 $X$ is homeomorphic to the space of homogeneous prime ideals in the group cohomology ring
$X$ is homeomorphic to the space of homogeneous prime ideals in the group cohomology ring 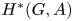 $H^*(G,A)$.
$H^*(G,A)$.
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 3
- Cited by



