Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T05:13:34.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmetic properties of Apéry-like numbers

Part of: Combinatorics Sequences and sets

Published online by Cambridge University Press:  20 October 2017

É. Delaygue
É. Delaygue*
Affiliation:
Institut Camille Jordan, Université Claude Bernard Lyon 1, 43 boulevard du 11 Novembre 1918, 69622 Villeurbanne cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide lower bounds for 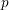$p$-adic valuations of multisums of factorial ratios which satisfy an Apéry-like recurrence relation: these include Apéry, Domb and Franel numbers, the numbers of abelian squares over a finite alphabet, and constant terms of powers of certain Laurent polynomials. In particular, we prove Beukers’ conjectures on the 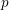$p$-adic valuation of Apéry numbers. Furthermore, we give an effective criterion for a sequence of factorial ratios to satisfy the 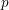$p$-Lucas property for almost all primes 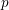$p$.

Keywords

Apéry numbersconstant terms of powers of Laurent polynomialsp-Lucas propertycongruences

MSC classification

Primary: 11B50: Sequences (mod $m$)
Secondary: 11B65: Binomial coefficients; factorials; $q$-identities 05A10: Factorials, binomial coefficients, combinatorial functions
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 2 , February 2018 , pp. 249 - 274
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almkvist, G. and Zudilin, W., Differential equations, mirror maps and zeta values , in Mirror symmetry, Vol. V, AMS/IP Studies in Advanced Mathematics, vol. 38 (American Mathematical Society, Providence, RI, 2006), 481–515.Google Scholar
Apéry, R., Irrationalité de 𝜁(2) et 𝜁(3) , Astérisque 61 (1979), 11–13.Google Scholar
Beukers, F., Some congruences for the Apéry numbers , J. Number Theory 21 (1985), 141–155.CrossRefGoogle Scholar
Beukers, F., Congruence properties of coefficients of solutions of Picard–Fuchs equations , Groupe de travail d’analyse ultramétrique 14 (1986–1987), 1–6; Exposé 11.Google Scholar
Beukers, F., Another congruence for the Apéry numbers , J. Number Theory 25 (1987), 201–210.CrossRefGoogle Scholar
Beukers, F. and Stienstra, J., On the Picard–Fuchs equation and the formal Brauer group of certain elliptic K3-surfaces , Math. Ann. 271 (1985), 269–304.Google Scholar
Borwein, J. M., Nuyens, D., Straub, A. and Wan, J., Some arithmetic properties of short random walk integrals , Ramanujan J. 26 (2011), 109–132.Google Scholar
Calkin, N. J., Factors of sums of powers of binomial coefficients , Acta Arith. 86 (1998), 17–26.Google Scholar
Catalan, E., Sur un développement de l’intégrale elliptique de première espèce et sur une suite de nombres entiers , Mém. Acad. R. Sci. Lett. Beaux-Arts Belg. 46 (1885), 1–24.Google Scholar
Chowla, S., Cowles, J. and Cowles, M., Congruence properties of Apéry numbers , J. Number Theory 12 (1980), 188–190.Google Scholar
Conway, J. H. and Guy, R. K., The book of numbers (Springer, New York, 1996), 106.Google Scholar
Coster, M. J., Congruence properties of coefficients of certain algebraic power series , Compositio Math. 68 (1988), 41–57.Google Scholar
Delaygue, E., A criterion for the integrality of the Taylor coefficients of mirror maps in several variables , Adv. Math. 234 (2013), 414–452.Google Scholar
Delaygue, E., Rivoal, T. and Roques, J., On Dwork’s p-adic formal congruences theorem and hypergeometric mirror maps , Mem. Amer. Math. Soc. 246 (2017), 100 pp.Google Scholar
Deutsch, E. and Sagan, B. E., Congruences for Catalan and Motzkin numbers and related sequences , J. Number Theory 117 (2006), 191–215.Google Scholar
Franel, J., On a question of Laisant , L’intermédiaire des Mathématiciens 1 (1894), 45–47.Google Scholar
Franel, J., On a question of J. Franel , L’intermédiaire des Mathématiciens 2 (1895), 33–35.Google Scholar
Gessel, I., Some congruences for Apéry numbers , J. Number Theory 14 (1982), 362–368.Google Scholar
Kummer, E., Über die Ergänzungssätze zu den allgemeinen Reciprocitätsgesetzen , J. reine angew. Math. 44 (1852), 93–146.Google Scholar
Landau, E., Sur les conditions de divisibilité d’un produit de factorielles par un autre , Nouv. Ann. Math. (3) 19 (1900), 344–362.Google Scholar
Lucas, E., Sur les congruences des nombres eulériens et les coefficients différentiels des fonctions trigonométriques suivant un module premier , Bull. Soc. Math. France 6 (1878), 49–54.Google Scholar
Mellit, A. and Vlasenko, M., Dwork’s congruences for the constant terms of powers of a Laurent polynomial , Int. J. Number Theory 12 (2016), 313–321.CrossRefGoogle Scholar
Mimura, Y., Congruence properties of Apéry numbers , J. Number Theory 16 (1983), 138–146.CrossRefGoogle Scholar
The On-line encyclopedia of integer sequences, published electronically at http://oeis.org (2013).Google Scholar
Richmond, L. B. and Shallit, J., Counting abelian squares , Electron. J. Combin. 16 (2009), Research paper 72, 9 pp.CrossRefGoogle Scholar
Samol, K. and van Straten, D., Dwork congruences and reflexive polytopes , Ann. Math. Québec 39 (2015), 185–203.Google Scholar
Zagier, D., Integral solutions of Apéry-like recurrence equations , in Groups and symmetries, CRM Proceedings and Lecture Notes, vol. 47 (American Mathematical Society, Providence, RI, 2009), 349–366.Google Scholar