Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gao, Ziyang
2020.
Mixed Ax–Schanuel for the universal abelian varieties and some applications.
Compositio Mathematica,
Vol. 156,
Issue. 11,
p.
2263.
Gao, Ziyang
2020.
Generic rank of Betti map and unlikely intersections.
Compositio Mathematica,
Vol. 156,
Issue. 12,
p.
2469.
Daw, Christopher
Javanpeykar, Ariyan
and
Kühne, Lars
2020.
Effective estimates for the degrees of maximal special subvarieties.
Selecta Mathematica,
Vol. 26,
Issue. 1,
Orr, Martin
2021.
GALOIS CONJUGATES OF SPECIAL POINTS AND SPECIAL SUBVARIETIES IN SHIMURA VARIETIES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 20,
Issue. 3,
p.
1075.
Aslanyan, Vahagn
Eterović, Sebastian
and
Kirby, Jonathan
2021.
Differential existential closedness for the 𝑗-function.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 4,
p.
1417.
Aslanyan, Vahagn
2021.
Ax-Schanuel and strong minimality for the j-function.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 1,
p.
102871.
Borovoi, Mikhail
Daw, Christopher
and
Ren, Jinbo
2021.
Conjugation of semisimple subgroups over real number fields of bounded degree.
Proceedings of the American Mathematical Society,
Vol. 149,
Issue. 12,
p.
4973.
Chen, Ke
Lu, Xin
and
Zuo, Kang
2021.
On CM points away from the Torelli locus.
Journal of the London Mathematical Society,
Vol. 104,
Issue. 3,
p.
1363.
Daw, Christopher
and
Orr, Martin
2022.
Quantitative Reduction Theory and Unlikely Intersections.
International Mathematics Research Notices,
Vol. 2022,
Issue. 20,
p.
16138.
Aslanyan, Vahagn
2022.
Weak modular Zilber–Pink with derivatives.
Mathematische Annalen,
Vol. 383,
Issue. 1-2,
p.
433.
Huang, Jiaxing
and
Ng, Tuen Wai
2022.
Ax–Schanuel type theorems on functional transcendence via Nevanlinna theory.
Mathematische Zeitschrift,
Vol. 300,
Issue. 2,
p.
1639.
Ngaiming, Mok
2022.
Complex differential geometry and its applications.
Chinese Science Bulletin,
Vol. 67,
Issue. 32,
p.
3737.
Aslanyan, Vahagn
2022.
Adequate predimension inequalities in differential fields.
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 1,
p.
103030.
Daw, Christopher
and
Orr, Martin
2023.
Lattices with skew-Hermitian forms over division algebras and unlikely intersections.
Journal de l’École polytechnique — Mathématiques,
Vol. 10,
Issue. ,
p.
1097.
Urbanik, David
2023.
Sets of special subvarieties of bounded degree.
Compositio Mathematica,
Vol. 159,
Issue. 3,
p.
616.
Gao, Ziyang
and
Klingler, Bruno
2024.
The Ax–Schanuel conjecture for variations of mixed Hodge structures.
Mathematische Annalen,
Vol. 388,
Issue. 4,
p.
3847.
Baldi, Gregorio
Klingler, Bruno
and
Ullmo, Emmanuel
2024.
On the distribution of the Hodge locus.
Inventiones mathematicae,
Vol. 235,
Issue. 2,
p.
441.
Lam, Yeuk Hay Joshua
and
Tripathy, Arnav
2024.
Attractors are not algebraic.
Compositio Mathematica,
Vol. 160,
Issue. 5,
p.
1073.
Papas, Georgios
2024.
Some Cases of the Zilber–Pink Conjecture for Curves in 𝒜g
.
International Mathematics Research Notices,
Vol. 2024,
Issue. 5,
p.
4160.
Aslanyan, Vahagn
and
Daw, Christopher
2024.
A note on unlikely intersections in Shimura varieties.
Journal of Number Theory,
Vol. 260,
Issue. ,
p.
212.
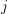 $j$-function and, with Mok, have recently announced a proof of its generalization to any (pure) Shimura variety. We refer to this generalization as the hyperbolic Ax–Schanuel conjecture. In this article, we show that the hyperbolic Ax–Schanuel conjecture can be used to reduce the Zilber–Pink conjecture for Shimura varieties to a problem of point counting. We further show that this point counting problem can be tackled in a number of cases using the Pila–Wilkie counting theorem and several arithmetic conjectures. Our methods are inspired by previous applications of the Pila–Zannier method and, in particular, the recent proof by Habegger and Pila of the Zilber–Pink conjecture for curves in abelian varieties.
$j$-function and, with Mok, have recently announced a proof of its generalization to any (pure) Shimura variety. We refer to this generalization as the hyperbolic Ax–Schanuel conjecture. In this article, we show that the hyperbolic Ax–Schanuel conjecture can be used to reduce the Zilber–Pink conjecture for Shimura varieties to a problem of point counting. We further show that this point counting problem can be tackled in a number of cases using the Pila–Wilkie counting theorem and several arithmetic conjectures. Our methods are inspired by previous applications of the Pila–Zannier method and, in particular, the recent proof by Habegger and Pila of the Zilber–Pink conjecture for curves in abelian varieties.

