Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-09T01:37:18.026Z Has data issue: false hasContentIssue false
  • English
  • Français

Applications du théorème d’Ax–Lindemann hyperbolique

Part of: Arithmetic algebraic geometry Model theory Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  19 November 2013

Emmanuel Ullmo
Emmanuel Ullmo*
Affiliation:
Départment de Mathématiques, Université Paris-Sud, 91405 Orsay, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We explain how the André–Oort conjecture for a general Shimura variety can be deduced from the hyperbolic Ax–Lindemann conjecture, a good lower bound for Galois orbits of special points and the definability, in the $o$-minimal structure 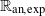${ \mathbb{R} }_{\mathrm{an} , \mathrm{exp} } $, of the restriction to a fundamental set of the uniformizing map of a Shimura variety. These ingredients are known in some important cases. As a consequence a proof of the André–Oort conjecture for projective special subvarieties of 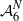${ \mathcal{A} }_{6}^{N} $ for an arbitrary integer $N$ is given.

Keywords

arithmetic geometryShimura varietieso-minimality

MSC classification

Secondary: 03C64: Model theory of ordered structures; o-minimality 11G18: Arithmetic aspects of modular and Shimura varieties 14G35: Modular and Shimura varieties
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 2 , February 2014 , pp. 175 - 190
Copyright
© The Author(s) 2013 

References

Borel, A., Introduction aux groupes arithmétiques (Hermann, Paris, 1969).Google Scholar
Chai, C.-L. and Oort, F., Abelian varieties isogenous to a Jacobian, Ann. of Math. (2) 176 (2012), 589–635.Google Scholar
Clozel, L. and Ullmo, E., Equidistribution adèlique des tores et équidistribution des points CM, Doc. Math. Extra Volume $\colon $ John H. Coates’ Sixtieth Birthday (2006), 233–260 (in French).Google Scholar
Eskin, A., Mozes, S. and Shah, N., Non divergence of translates of certain algebraic measures, Geom. Funct. Anal. 7 (1997), 48–80.Google Scholar
Fortuna, E. and Lojasiewicz, S., Sur l’algébricité des ensembles analytiques complexes, J. Reine Angew. Math. 329 (1981), 215–220.Google Scholar
Klingler, B. and Yafaev, A., The André–Oort conjecture, Preprint (2006).Google Scholar
Margulis, G. A., Discrete subgroups of semisimple Lie groups (Springer, Berlin, 1989).Google Scholar
Moonen, B., Linearity properties of Shimura varieties. I, J. Algebraic Geom. 7 (1998), 539–567.Google Scholar
Peterzil, Y. and Starchenko, S., Definability of restricted theta functions and families of Abelian varieties, Preprint (2011).Google Scholar
Pila, J., O-minimality and the Andre–Oort conjecture for ${ \mathbb{C} }^{n} $ , Ann. of Math. (2) 173 (2011), 1779–1840.Google Scholar
Pila, J. and Wilkie, A., The rational points on a definable set, Duke Math. J. 133 (2006), 591–616.Google Scholar
Pila, J. and Tsimerman, J., The André–Oort conjecture for the moduli space of Abelian surfaces, Preprint (2011), arXiv $: $ 1106.4023 [math.NT].Google Scholar
Pila, J. and Tsimerman, J., Ax-Lindemann for ${ \mathcal{A} }_{g} $ , Preprint (2012), arXiv $: $ 1206.2663 [math.NT].Google Scholar
Pila, J. and Zannier, U., Rational points in periodic analytic sets and the Manin–Mumford conjecture, Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 19 (2008), 149–162.Google Scholar
Tsimerman, J., Brauer–Siegel for arithmetic tori and lower bounds for Galois orbits of special points, Preprint (2011).Google Scholar
Ullmo, E., Equidistribution des sous-variétés spéciales II, J. Reine Angew. Math. (2006), 1–24.Google Scholar
Ullmo, E. and Yafaev, A., Galois orbits and equidistribution of special subvarieties $: $ towards the André–Oort conjecture, Preprint (2006) $; $ version 2012 disponible à la page webhttp://www.math.u-psud.fr/~ullmo/.Google Scholar
Ullmo, E. and Yafaev, A., A characterisation of special subvarieties, Mathematika 57 (2011), 263–273.Google Scholar
Ullmo, E. and Yafaev, A., Nombre de classes des tores de multiplication complexe et bornes inférieures pour les orbites Galoisiennes de points spéciaux, Preprint (2011).Google Scholar
Ullmo, E. and Yafaev, A., The hyperbolic Ax-Lindemann conjecture in the compact case, Preprint (2012).Google Scholar