Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yin, Qizheng
and
Zhu, Yi
2018.
𝔸1-equivalence of zero cycles on surfaces,
II.
Annals of K-Theory,
Vol. 3,
Issue. 3,
p.
379.
Krishna, Amalendu
2019.
Murthy’s conjecture on 0-cycles.
Inventiones mathematicae,
Vol. 217,
Issue. 2,
p.
549.
IWASA, RYOMEI
and
KAI, WATARU
2019.
CHERN CLASSES WITH MODULUS.
Nagoya Mathematical Journal,
Vol. 236,
Issue. ,
p.
84.
Binda, Federico
and
Saito, Shuji
2019.
RELATIVE CYCLES WITH MODULI AND REGULATOR MAPS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 18,
Issue. 06,
p.
1233.
Gupta, Rahul
and
Krishna, Amalendu
2019.
𝐾-theory and 0-cycles on schemes.
Journal of Algebraic Geometry,
Vol. 29,
Issue. 3,
p.
547.
Iwasa, Ryomei
2019.
Relative K0 and relative cycle class map.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 1,
p.
48.
Binda, Federico
2020.
A motivic homotopy theory without $$\mathbb {A}^{1}$$-invariance.
Mathematische Zeitschrift,
Vol. 295,
Issue. 3-4,
p.
1475.
Kai, Wataru
2020.
A Moving Lemma for Algebraic Cycles With Modulus and Contravariance.
International Mathematics Research Notices,
Vol. 2021,
Issue. 1,
p.
475.
Iwasa, Ryomei
and
Kai, Wataru
2021.
ISOMORPHISMS UP TO BOUNDED TORSION BETWEEN RELATIVE -GROUPS AND CHOW GROUPS WITH MODULUS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 20,
Issue. 6,
p.
1947.
Binda, Federico
and
Krishna, Amalendu
2022.
Suslin homology via cycles with modulus and applications.
Transactions of the American Mathematical Society,
Binda, Federico
and
Krishna, Amalendu
2022.
Zero-cycle groups on algebraic varieties.
Journal de l’École polytechnique — Mathématiques,
Vol. 9,
Issue. ,
p.
281.
Gupta, Rahul
and
Krishna, Amalendu
2022.
Idele class groups with modulus.
Advances in Mathematics,
Vol. 404,
Issue. ,
p.
108376.
Binda, Federico
Krishna, Amalendu
and
Saito, Shuji
2022.
Bloch’s formula for 0-cycles with modulus and higher-dimensional class field theory.
Journal of Algebraic Geometry,
Vol. 32,
Issue. 2,
p.
323.
Rülling, Kay
Sugiyama, Rin
and
Yamazaki, Takao
2022.
Tensor structures in the theory of modulus presheaves with transfers.
Mathematische Zeitschrift,
Vol. 300,
Issue. 1,
p.
929.
Ghosh, Mainak
and
Krishna, Amalendu
2023.
ZERO-CYCLES ON NORMAL PROJECTIVE VARIETIES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 5,
p.
2241.
Binda, Federico
Merici, Alberto
and
Saito, Shuji
2023.
Derived log Albanese sheaves.
Advances in Mathematics,
Vol. 417,
Issue. ,
p.
108936.
Lüders, Morten
2024.
Zero-cycles in families of rationally connected varieties.
Selecta Mathematica,
Vol. 30,
Issue. 4,
Krishna, Amalendu
Rathore, Jitendra
and
Sadhukhan, Samiron
2024.
Duality theorems for curves over local fields.
Transactions of the American Mathematical Society, Series B,
Vol. 11,
Issue. 28,
p.
945.
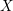 $X$ and an effective Cartier divisor
$X$ and an effective Cartier divisor 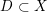 $D\subset X$, we show that the cohomological Chow group of 0-cycles on the double of
$D\subset X$, we show that the cohomological Chow group of 0-cycles on the double of 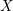 $X$ along
$X$ along 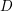 $D$ has a canonical decomposition in terms of the Chow group of 0-cycles
$D$ has a canonical decomposition in terms of the Chow group of 0-cycles 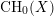 $\text{CH}_{0}(X)$ and the Chow group of 0-cycles with modulus
$\text{CH}_{0}(X)$ and the Chow group of 0-cycles with modulus 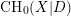 $\text{CH}_{0}(X|D)$ on
$\text{CH}_{0}(X|D)$ on 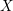 $X$. When
$X$. When 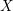 $X$ is projective, we construct an Albanese variety with modulus and show that this is the universal regular quotient of
$X$ is projective, we construct an Albanese variety with modulus and show that this is the universal regular quotient of 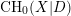 $\text{CH}_{0}(X|D)$. As a consequence of the above decomposition, we prove the Roitman torsion theorem for the 0-cycles with modulus. We show that
$\text{CH}_{0}(X|D)$. As a consequence of the above decomposition, we prove the Roitman torsion theorem for the 0-cycles with modulus. We show that 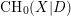 $\text{CH}_{0}(X|D)$ is torsion-free and there is an injective cycle class map
$\text{CH}_{0}(X|D)$ is torsion-free and there is an injective cycle class map 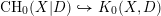 $\text{CH}_{0}(X|D){\hookrightarrow}K_{0}(X,D)$ if
$\text{CH}_{0}(X|D){\hookrightarrow}K_{0}(X,D)$ if 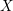 $X$ is affine. For a smooth affine surface
$X$ is affine. For a smooth affine surface 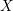 $X$, this is strengthened to show that
$X$, this is strengthened to show that 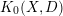 $K_{0}(X,D)$ is an extension of
$K_{0}(X,D)$ is an extension of 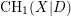 $\text{CH}_{1}(X|D)$ by
$\text{CH}_{1}(X|D)$ by 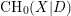 $\text{CH}_{0}(X|D)$.
$\text{CH}_{0}(X|D)$.

