Article contents
Twisted GGP problems and conjectures
Published online by Cambridge University Press: 31 July 2023
Abstract
In a series of three earlier papers, we considered a family of restriction problems for classical groups (over local and global fields) and proposed precise answers to these problems using the local and global Langlands correspondence. These restriction problems were formulated in terms of a pair 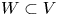 $W \subset V$ of orthogonal, Hermitian, symplectic, or skew-Hermitian spaces. In this paper, we consider a twisted variant of these conjectures in one particular case: that of a pair of skew-Hermitian spaces
$W \subset V$ of orthogonal, Hermitian, symplectic, or skew-Hermitian spaces. In this paper, we consider a twisted variant of these conjectures in one particular case: that of a pair of skew-Hermitian spaces  $W = V$.
$W = V$.
Keywords
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
Footnotes
WTG is partially supported by an MOE Tier 1 grant R-146-000-320-114. DP thanks the Science and Engineering Research Board of the Department of Science and Technology, India for its support through the JC Bose National Fellowship of the Govt. of India, project number JBR/2020/000006. The paper was finalized when the two of us, WTG and DP, were at the Erwin Schrödinger Institute, Vienna in April 2022. We thank ESI for its excellent program which brought us together there.
References
- 1
- Cited by



