Article contents
Systolic ratio, index of closed orbits and convexity for tight contact forms on the three-sphere
Published online by Cambridge University Press: 06 November 2018
Abstract
We construct a dynamically convex contact form on the three-sphere whose systolic ratio is arbitrarily close to 2. This example is related to a conjecture of Viterbo, whose validity would imply that the systolic ratio of a convex contact form does not exceed 1. We also construct, for every integer 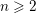 $n\geqslant 2$, a tight contact form with systolic ratio arbitrarily close to
$n\geqslant 2$, a tight contact form with systolic ratio arbitrarily close to  $n$ and with suitable bounds on the mean rotation number of all the closed orbits of the induced Reeb flow.
$n$ and with suitable bounds on the mean rotation number of all the closed orbits of the induced Reeb flow.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
Footnotes
The research of A. Abbondandolo and B. Bramham is supported by the SFB/TRR 191 ‘Symplectic Structures in Geometry, Algebra and Dynamics’, funded by the Deutsche Forschungsgemeinschaft. P. A. S. Salomão is supported by the FAPESP grant 2016/25053-8 and the CNPq grant 306106/2016-7. U. L. Hryniewicz was supported by CNPq grant 309966/2016-7 and by the Humboldt Foundation; he also acknowledges the generous hospitality of the Mathematics Department of the Ruhr-Universität Bochum.
References
- 5
- Cited by


