Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-12T21:09:33.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Subconvexity and equidistribution of Heegner points in the level aspect

Part of: Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  17 June 2013

Sheng-Chi Liu ,
Riad Masri  and
Matthew P. Young
Sheng-Chi Liu
Affiliation:
Department of Mathematics, Mailstop 3368, Texas A&M University, College Station, TX 77843-3368, USA email [email protected]@[email protected]
Riad Masri
Affiliation:
Department of Mathematics, Mailstop 3368, Texas A&M University, College Station, TX 77843-3368, USA email [email protected]@[email protected]
Matthew P. Young
Affiliation:
Department of Mathematics, Mailstop 3368, Texas A&M University, College Station, TX 77843-3368, USA email [email protected]@[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 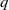$q$ be a prime and $- D\lt - 4$ be an odd fundamental discriminant such that 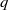$q$ splits in 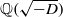$ \mathbb{Q} ( \sqrt{- D} )$. For 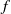$f$ a weight-zero Hecke–Maass newform of level 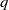$q$ and 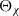${\Theta }_{\chi } $ the weight-one theta series of level 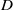$D$ corresponding to an ideal class group character 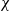$\chi $ of 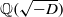$ \mathbb{Q} ( \sqrt{- D} )$, we establish a hybrid subconvexity bound for 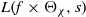$L(f\times {\Theta }_{\chi } , s)$ at 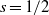$s= 1/ 2$ when 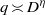$q\asymp {D}^{\eta } $ for 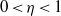$0\lt \eta \lt 1$. With this circle of ideas, we show that the Heegner points of level 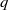$q$ and discriminant 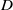$D$ become equidistributed, in a natural sense, as 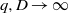$q, D\rightarrow \infty $ for 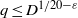$q\leq {D}^{1/ 20- \varepsilon } $. Our approach to these problems is connected to estimating the 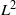${L}^{2} $-restriction norm of a Maass form of large level 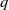$q$ when restricted to the collection of Heegner points. We furthermore establish bounds for quadratic twists of Hecke–Maass 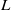$L$-functions with simultaneously large level and large quadratic twist, and hybrid bounds for quadratic Dirichlet 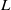$L$-functions in certain ranges.

Keywords

subconvexityequidistributionHeegner pointsL4 norm

MSC classification

Secondary: 11M41: Other Dirichlet series and zeta functions
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 7 , July 2013 , pp. 1150 - 1174
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biró, A., Cycle integrals of Maass forms of weight 0 and Fourier coefficients of Maass forms of weight 1/2, Acta Arith. 94 (2000), 103–152; 54 (2004), 831–847.CrossRefGoogle Scholar
Blomer, V., On the 4-norm of an automorphic form, J. Eur. Math. Soc. (JEMS), to appear, math.NT/1110.4717.Google Scholar
Blomer, V. and Harcos, G., Hybrid bounds for twisted $L$-functions, J. Reine Angew. Math. 621 (2008), 53–79.Google Scholar
Blomer, V., Khan, R. and Young, M., Distribution of Mass of holomorphic cusp forms, Duke Math. J., to appear, Preprint (2012), math.NT/1203.2573.Google Scholar
Conrey, B. and Iwaniec, H., The cubic moment of central values of automorphic $L$-functions, Ann. of Math. (2) 151 (2000), 1175–1216.CrossRefGoogle Scholar
Duke, W., Hyperbolic distribution problems and half-integral weight Maass forms, Invent. Math. 92 (1988), 73–90.Google Scholar
Duke, W., Friedlander, J. and Iwaniec, H., Class group $L$-functions, Duke Math. J. 79 (1995), 1–56.CrossRefGoogle Scholar
Feigon, B. and Whitehouse, D., Averages of central $L$-values of Hilbert modular forms with an application to subconvexity, Duke Math. J. 149 (2009), 347–410.Google Scholar
Gelbart, S. and Jacquet, H., A relation between automorphic representations of $GL(2)$ and $GL(3)$, Ann. Sci. Éc. Norm. Supér. (4) 11 (1978), 471–542.CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M., Table of integrals, series, and products, sixth edition (Academic Press, San Diego, CA, 2000), translated from Russian.Google Scholar
Gross, B. and Zagier, D., Heegner points and derivatives of $L$-series, Invent. Math. 84 (1986), 225–320.Google Scholar
Harcos, G. and Michel, P., The subconvexity problem for Rankin–Selberg $L$-functions and equidistribution of Heegner points. II, Invent. Math. 163 (2006), 581–655.CrossRefGoogle Scholar
Harcos, G. and Templier, N., On the sup-norm of Maass cusp forms of large level. III, Math. Ann. 356 (2013), 209–216.CrossRefGoogle Scholar
Heath-Brown, D. R., Hybrid bounds for Dirichlet $L$-functions, Invent. Math. 47 (1978), 149–170.CrossRefGoogle Scholar
Heath-Brown, D. R., Hybrid bounds for Dirichlet $L$-functions. II, Q. J. Math. Oxford Ser. (2) 31 (1980), 157–167.CrossRefGoogle Scholar
Holowinsky, R. and Munshi, R., Level Aspect Subconvexity For Rankin–Selberg $L$-functions, Preprint (2012), math.NT1203.1300.Google Scholar
Holowinsky, R. and Templier, N., First moment of Rankin–Selberg central $L$-values and subconvexity in the level aspect, doi:10.1007/S11139-012-9454-y, March 2013.Google Scholar
Huxley, M. N. and Watt, N., Hybrid bounds for Dirichlet’s $L$-function, Math. Proc. Cambridge Philos. Soc. 129 (2000), 385–415.CrossRefGoogle Scholar
Iwaniec, H., Fourier coefficients of modular forms of half-integral weight, Invent. Math. 87 (1987), 385–401.Google Scholar
Iwaniec, H., Topics in classical automorphic forms, Graduate Studies in Mathematics, vol. 17 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Iwaniec, H., Luo, W. and Sarnak, P., Low lying zeros of families of $L$-functions., Publ. Math. Inst. Hautes Études Sci. (2001), 55–131.Google Scholar
Katok, S. and Sarnak, P., Heegner points, cycles and Maass forms, Israel J. Math. 84 (1993), 193–227.Google Scholar
Kohnen, W. and Sengupta, J., On quadratic character twists of Hecke $L$-functions attached to cusp forms of varying weights at the central point, Acta Arith. 99 (2001), 61–66.CrossRefGoogle Scholar
Kowalski, E., Michel, P. and VanderKam, J., Rankin–Selberg $L$-functions in the level aspect, Duke Math. J. 114 (2002), 123–191.Google Scholar
Li, X., Upper bounds on $L$-functions at the edge of the critical strip, Int. Math. Res. Not. IMRN (2010), 727–755.Google Scholar
Li, X. and Young, M., The ${L}^{2} $ restriction norm of a ${\mathrm{GL} }_{3} $ Maass form, Compositio Math. 148 (2012), 675–717.Google Scholar
Michel, P., The subconvexity problem for Rankin–Selberg $L$-functions and equidistribution of Heegner points, Ann. of Math. (2) 160 (2004), 185–236.Google Scholar
Michel, P. and Ramakrishnan, D., Consequences of the Gross–Zagier formulae: stability of average $L$-values, subconvexity, and non-vanishing mod $p$, Number Theory, Analysis and Geometry (Springer, New York, 2012), 437–459.Google Scholar
Michel, P. and Venkatesh, A., Equidistribution, $L$-functions and ergodic theory: on some problems of Yu. Linnik, in International Congress of Mathematicians. Vol. II (European Mathematical Society, Zürich, 2006), 421–457.Google Scholar
Michel, P. and Venkatesh, A., Heegner points and non-vanishing of Rankin/Selberg $L$-functions, in Analytic number theory, Clay Mathematics Proceedings, vol. 7 (American Mathematical Society, Providence, RI, 2007), 169–183.Google Scholar
Michel, P. and Venkatesh, A., The subconvexity problem for ${\mathrm{GL} }_{2} $, Publ. Math. Inst. Hautes Études Sci. (2010), 171–271.Google Scholar
Munshi, R., On a hybrid bound for twisted $L$-values, Arch. Math. (Basel) 96 (2011), 235–245.Google Scholar
Nelson, P., Equidistribution of cusp forms in the level aspect, Duke Math. J. 160 (2011), 467–501.Google Scholar
Nelson, P., Stable averages of central values of Rankin–Selberg $L$-functions: some new variants, Preprint (2012), math.NT/1202.6313.Google Scholar
Schmidt, W., Equations over finite fields: An elementary approach, Lecture Notes in Mathematics, vol. 536 (Springer, Berlin, 1976).Google Scholar
Templier, N., A nonsplit sum of coefficients of modular forms, Duke Math. J. 157 (2011), 109–165.Google Scholar
Titchmarsh, E. C., The theory of the Riemann zeta-function, second edition (revised by D. R. Heath-Brown) (The Clarendon Press, Oxford University Press, New York, NY, 1986).Google Scholar
Waldspurger, J.-L., Sur les coefficients de Fourier des formes modulaires de poids demi-entier, J. Math. Pures Appl. (9) 60 (1981), 375–484.Google Scholar
Watt, N., On the mean squared modulus of a Dirichlet $L$-function over a short segment of the critical line, Acta Arith. 111 (2004), 307–403.Google Scholar
Watson, T., Rankin triple products and quantum chaos, Preprint (2008), arXiv:0810.0425.Google Scholar
Zhang, S. W., Gross–Zagier formula for ${\mathrm{GL} }_{2} $, Asian J. Math. 5 (2001), 183–290.Google Scholar
Zhang, S. W., Equidistribution of CM-points on quaternion Shimura varieties, Int. Math. Res. Not. IMRN (2005), 3657–3689.Google Scholar